基于观测的事件触发主从多智能体系统的一致性

夏孟瑶, 蒋海军, 于志永

(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)

在过去的几十年中,多智能体系统的一致性控制因其在编队控制、机器人团队等许多领域中的广泛应用而吸引了越来越多研究者的关注[1-4].达成一致的主要目的是通过智能体之间的信息交流,设计合适的控制器,最终使得所有智能体达到相同状态.作为控制领域的重要研究对象,多智能体系统的一致性问题可以分为无领导者一致性问题[5-6]和主从(领导跟随者)一致性问题.现如今,很多学者研究了主从多智能体一致性问题[7-8],其中文献[3,7]的一个共同特点是使用了每个智能体及其邻居的连续状态信息.

在研究一致性中,主要的任务是设计仅依赖智能体邻居信息的控制协议.事件触发作为一种合适的控制方法,其有利于多智能体之间的合作,也可以大大降低能源消耗,来节省有限的网络资源.因此,基于事件触发控制协议的优点,文献[9-15]采用事件触发控制方法解决了多智能体系统的一致性问题.Chen等[9]提出了基于观测的事件触发控制方法并研究了一般线性多智能体系统的主从一致性问题.Deng等[14]通过引入事件触发估计器,提出了2种分布式事件触发控制器用于解决无领导和领导跟随者线性多智能体的一致性问题,其中在事件触发机制中设计了自适应触发参数,以提高事件触发估计器的自我调节能力.这些研究结果验证了事件触发控制方法在不同多智能体系统中的有效性.

本文研究了一般线性主从多智能体系统的事件触发输出一致性问题.与现有的工作相比,本文的贡献主要包括以下2点:1) 基于事件触发控制方法，提出了一种输出反馈事件触发控制协议和分布式自适应事件触发控制协议;2) 对于具有线性动力学和一般无向网络拓扑的主从多智能体系统,提出了一种基于观测的自适应事件触发控制器,用以解决主从多智能体系统的一致性问题.

1 预备知识和模型描述

为了方便,先给出一些记号.‖·‖代表欧氏范数,⊗代表矩阵的Kronecker乘积,Rn代表n维实列向量,In是n维单位矩阵,1代表分量全为1的向量.对于矩阵P,PT、λ(P)和λ(P)分别代表P的转置、最小特征值和最大特征值,P>0代表P是一个正定矩阵,diag(·)代表对角矩阵.

考虑由N个智能体所组成的网络,网络拓扑由图G=(V,E)表示,其中V={1,2,…,N}表示节点集,E={(i,j)|i,j∈V}表示边集,记智能体i的邻居节点集为Ni={j|(i,j)∈E}.A=[aij]∈RN×N是图G的邻接矩阵,若(i,j)∈E,则aij>0,否则,aij=0.对于无向图G来说,aij=aji.记节点的度矩阵为D=diag(d1,d2,…,dN),其中d则图G的拉普拉斯矩阵定义为L=D-A.令矩阵H=L+B,其中B=diag(b1,b2,…,bN),如果智能体i能够接收到领导者的信息,则bi=1,否则,bi=0.

第i个智能体的动力学描述为

(1)

其中

xi(t)=(xi1(t),xi2(t),…,xin(t))∈Rn,

ui(t)∈Rm,yi(t)∈Rq

分别表示第i个智能体的状态、控制输入和输出.A∈Rn×n、B∈Rn×m、C∈Rq×n表示具有合适维数的常数矩阵.

领导者的动力学行为描述为

(2)

下面将给出一些相关的定义和假设.

假设 1.1拓扑图G是连通的,并且至少有一个跟随者可以接收到领导者的信息.

假设 1.2(A,B)是稳定的,(A,C)是可测的.

引理 1.1[16]L是具有N个点的无向连通图G的拉普拉斯矩阵,则L的特征值大小满足

0=λ1<λ2≤λ3≤…≤λN.

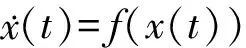
定义 1.1对于多智能体系统(1)和(2)的任意初值,如果满足

其中

x0(t)=(x01(t),x02(t),…,x0n(t))∈Rn,

i=1,2,…,N,

则称多智能体系统(1)和(2)达到一致.

2 主要结论

2.1 基于观测的事件触发稳定性首先,通过设计合适的增益矩阵K和输出事件触发条件,使系统达到渐近稳定.定义如下线性矩阵不等式

A

(5)

其中P1>0是对称正定矩阵.

定义

为输出测量误差,则第i个智能体的触发条件为

tik+1=inf{t>tik,fi(t)≥0},

(6)

其中

fi(t)=

‖e

其向量形式为

(L⊗K)ey(t),

(7)

其中

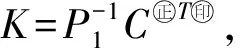
证明考虑如下Lyapunov函数

其中P1>0是正定矩阵.

将V1(t)沿着上式求导数

通过应用Young不等式,可得

进一步得到

由触发条件(6)可得

‖e

因此,有

令ε=λ(L),以及存在一个正交矩阵U,使得

ULU=diag(0,λ2,λ3,…,λN).

令

有

(I

根据线性矩阵不等式(5),可以得到

D+‖e

‖A‖‖eyi‖+‖Ayi(tik)‖+

(8)

其中

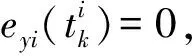
‖e

(9)

由事件触发函数可得

(10)

成立.

情形 2如果‖A‖=0,则根据(8)式,可得

同理,有如下不等式

2.2 自适应事件触发稳定性定义

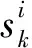
sik+1=inf{t>sik,gi(t)≥0},

(11)

其中

g

ηi(si

b

P2>0满足

P2A+AP2-2P2BBP2+Q=0,

其中Q>0是任意矩阵.

(12)

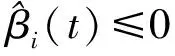
分布式自适应事件触发控制器设计如下

u

(13)

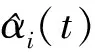
令σi(t)=xi(t)-x0(t)表示跟踪误差,根据系统(1)和(2)可得

(15)

其中

根据η(t)的定义,有

η(t)=(H⊗I

(H⊗In)σ(t)+(H⊗I

定理 2.2对于主从多智能体系统(1)和(2),考虑具有自适应的触发机制(11)和自适应控制器(13).如果假设1.1和1.2成立,则误差系统(15)渐近收敛到如下有界区域

其中

此外,记

βi=1/2((d

证明考虑如下的Lyapunov函数

V2(t)=V3(t)+V4(t),

(16)

其中

V3(t)=σ(t)(H⊗P2)σ(t),

ξ

对V2(t)求导得

(17)

令K1=BP2,Γ=P2BBP2,根据

的定义,有

σ(t)(H⊗(AP2+P2A)-αH2⊗Γ)σ(t)-

σ(t)(H⊗(AP2+P2A)-αH2⊗Γ)σ(t)-

根据Young不等式可得

(18)

然后,可以得到

Γηi(si

(19)

根据Young不等式有

(20)

结合(17)～(20)式可得

(21)

根据触发函数,可得

δe-ρ(t-sik),

(22)

(di+1)δe

(23)

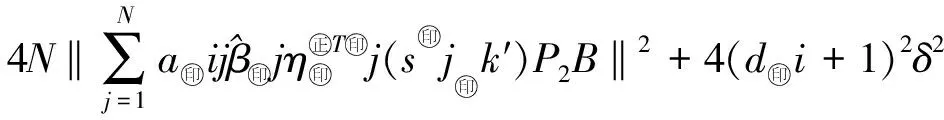
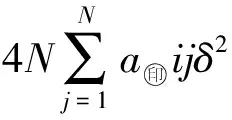
(24)

根据图理论可得

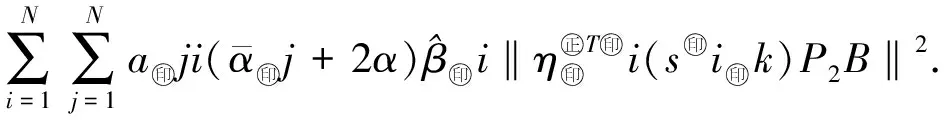
结合(21)和(24)～(25)式可得

σ(t)(H⊗(AP2+P2A)-αH2⊗Γ)σ(t)-

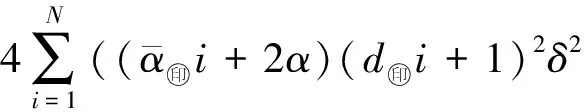
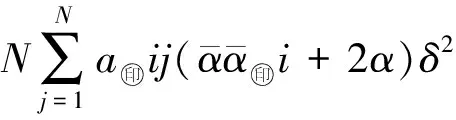
(26)

结合上述的分析过程,则有

αH2⊗Γ)σ(t)+φ≤

σ(t)(H⊗(AP2+P2A-2Γ))σ(t)+φ≤

-τλ(H)λ(Q)‖σ(t)‖2-

(1-τ)λ(H)λ(Q)‖σ(t)‖2+φ.(27)

对任意的τ>0,令

(1-τ)λ(H)λ(Q)‖σ(t)‖2>φ,

可得

最终可以得到

证毕.

触发函数(11)不会发生Zeno现象,其证明过程与定理1中排除Zeno现象的证明相同,此处省略证明过程.

注 2.1与文献[13]相比,本文提出了一种自适应事件触发控制器,通过设计合适的自适应参数,减少了智能体之间的信息交换并节省资源.最终,通过引理1.2,解决了主从多智能体系统一致性问题.

3 数值仿真

为了说明控制协议的有效性,给出如下的数值算例.

考虑具有5个智能体的多智能体系统(1),智能体之间的通讯拓扑用图1来描述,并选取如下矩阵

图 1 通讯拓扑图G

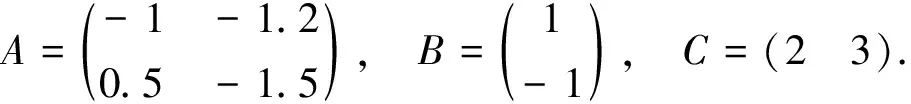
取系统的初值为:

x0(0)=(1.5,-1.5),x1(0)=(1,-0.5),

x2(0)=(0.5,0.5),x3(0)=(0.6,1),

x4(0)=(0,0.5).

自适应触发参数的初值为:

事件触发估计器参数为:

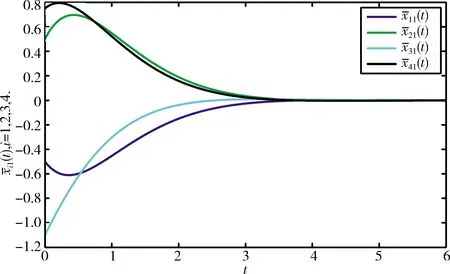
图 2 估计误差的状态轨迹

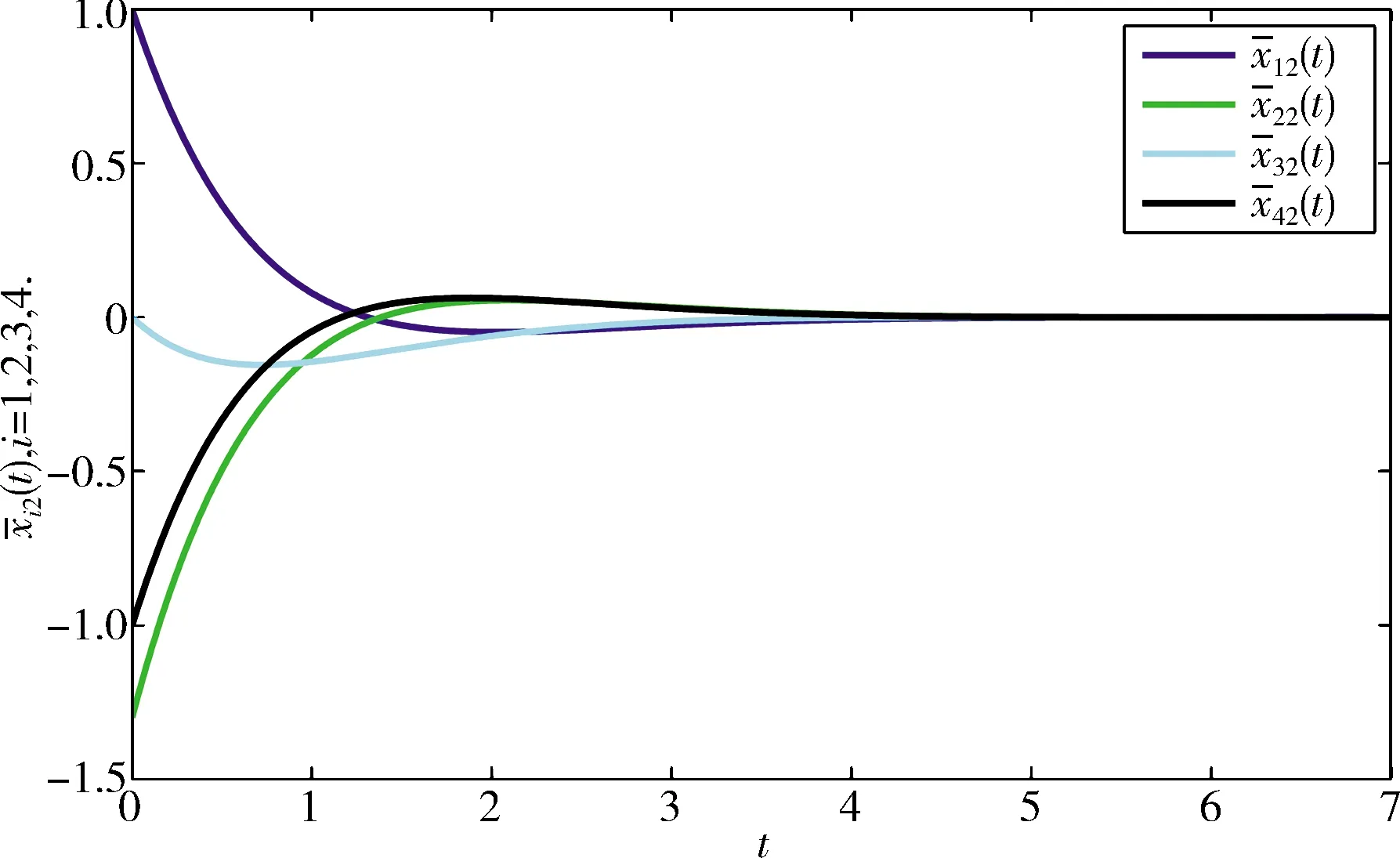
图 3 估计误差的状态轨迹

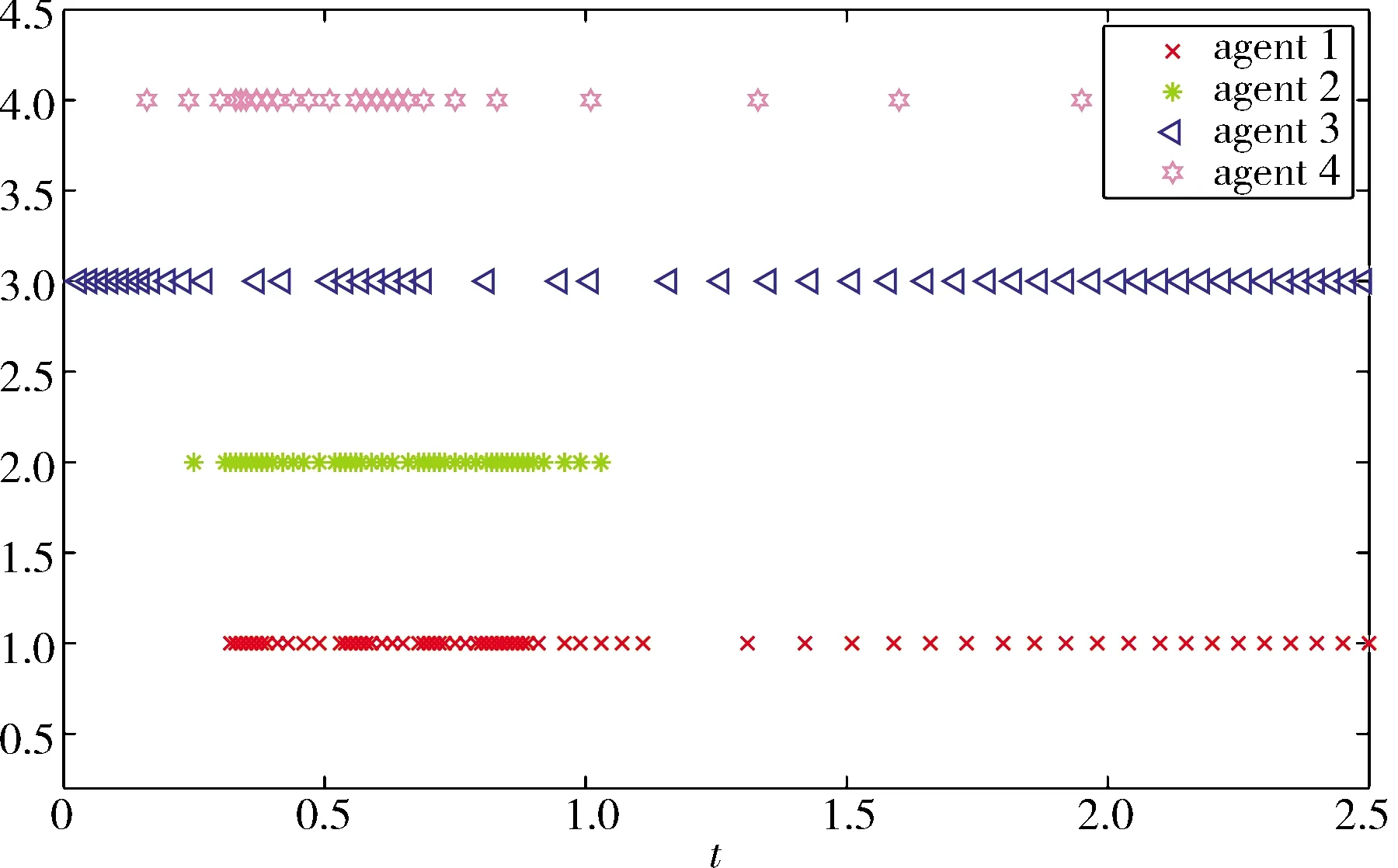
图 4 触发时刻

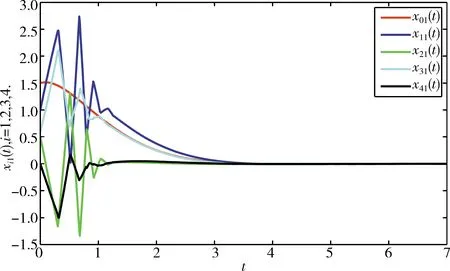
图 5 xi1的状态轨迹

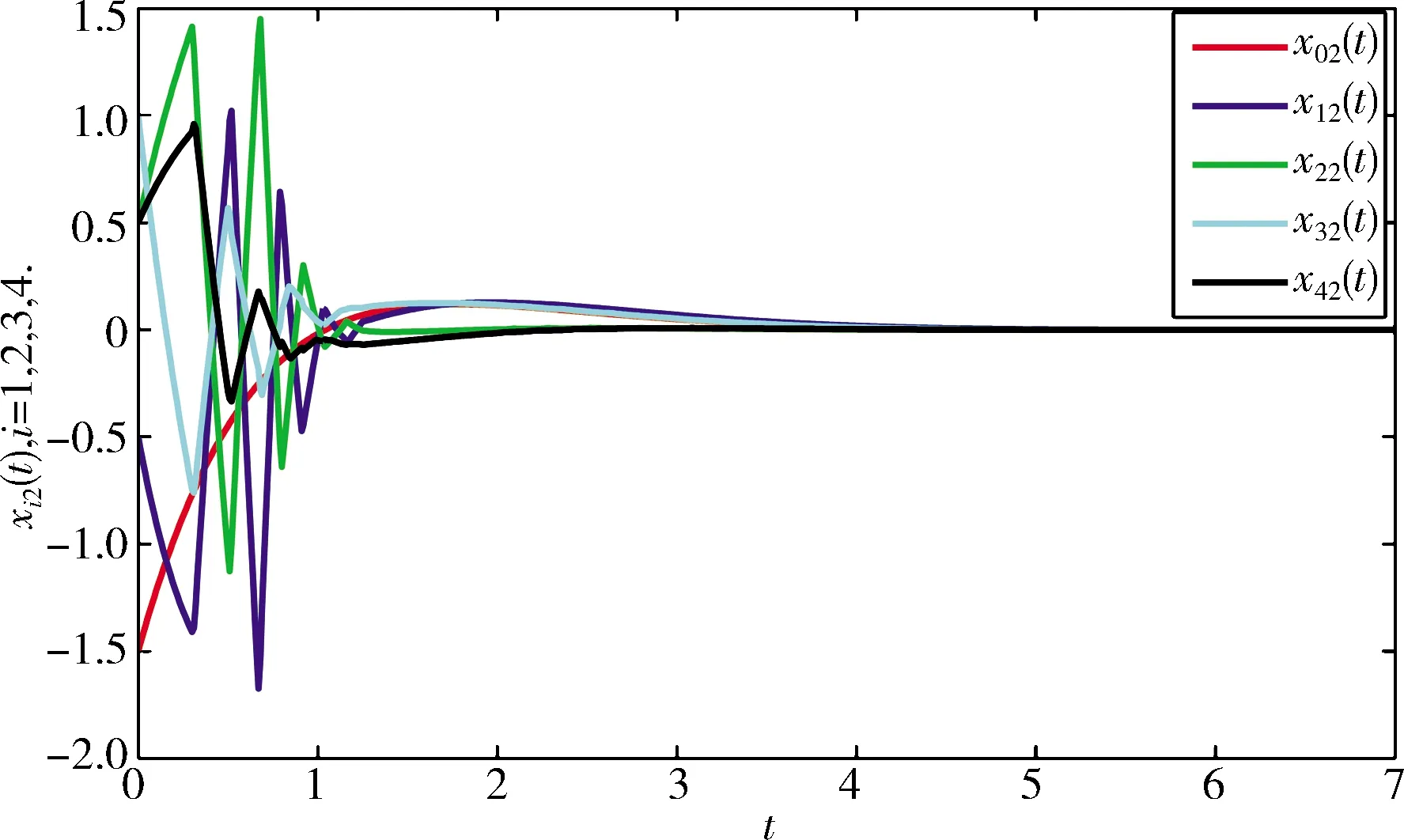
图6 xi2的状态轨迹

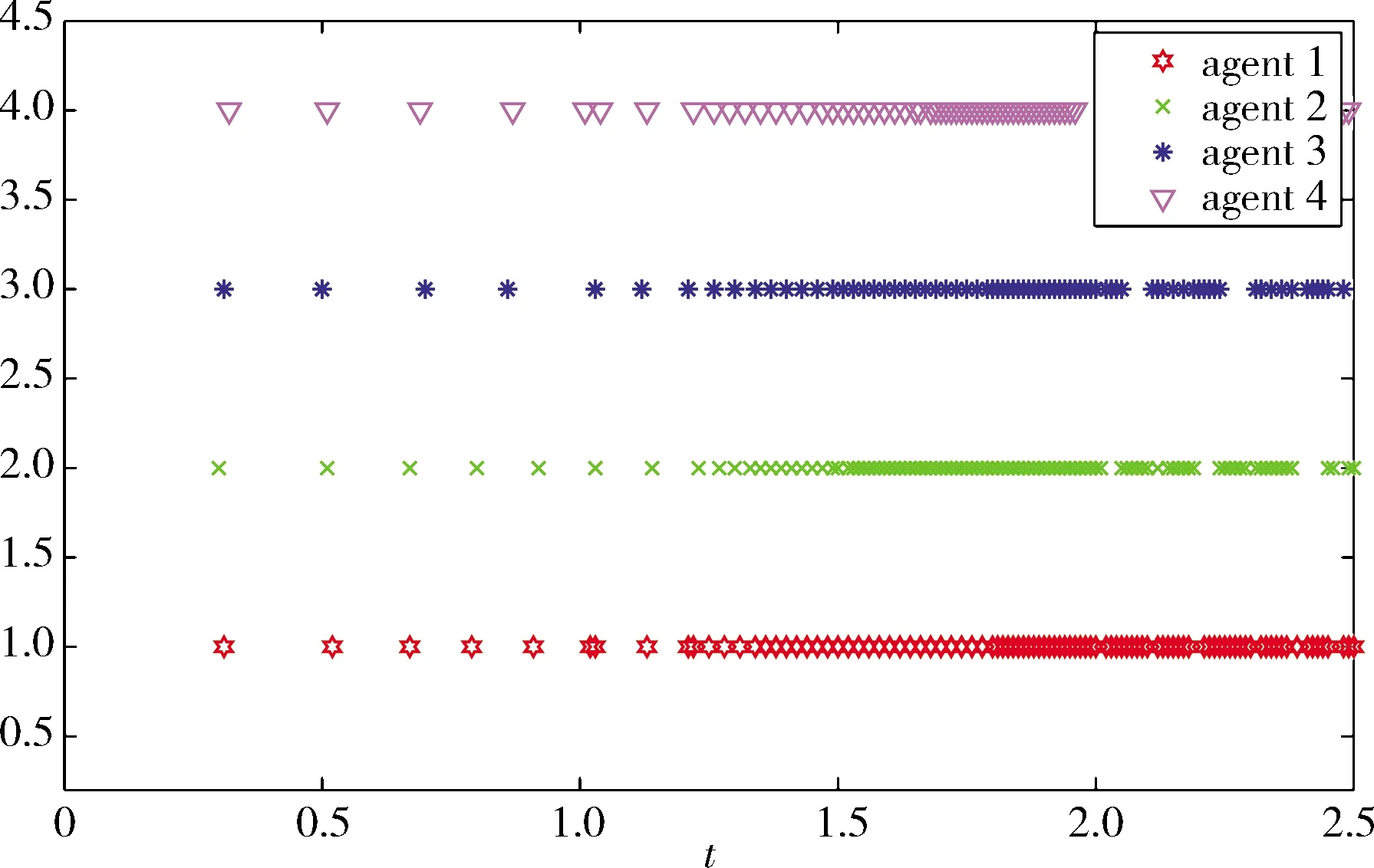
图7 智能体的触发时刻

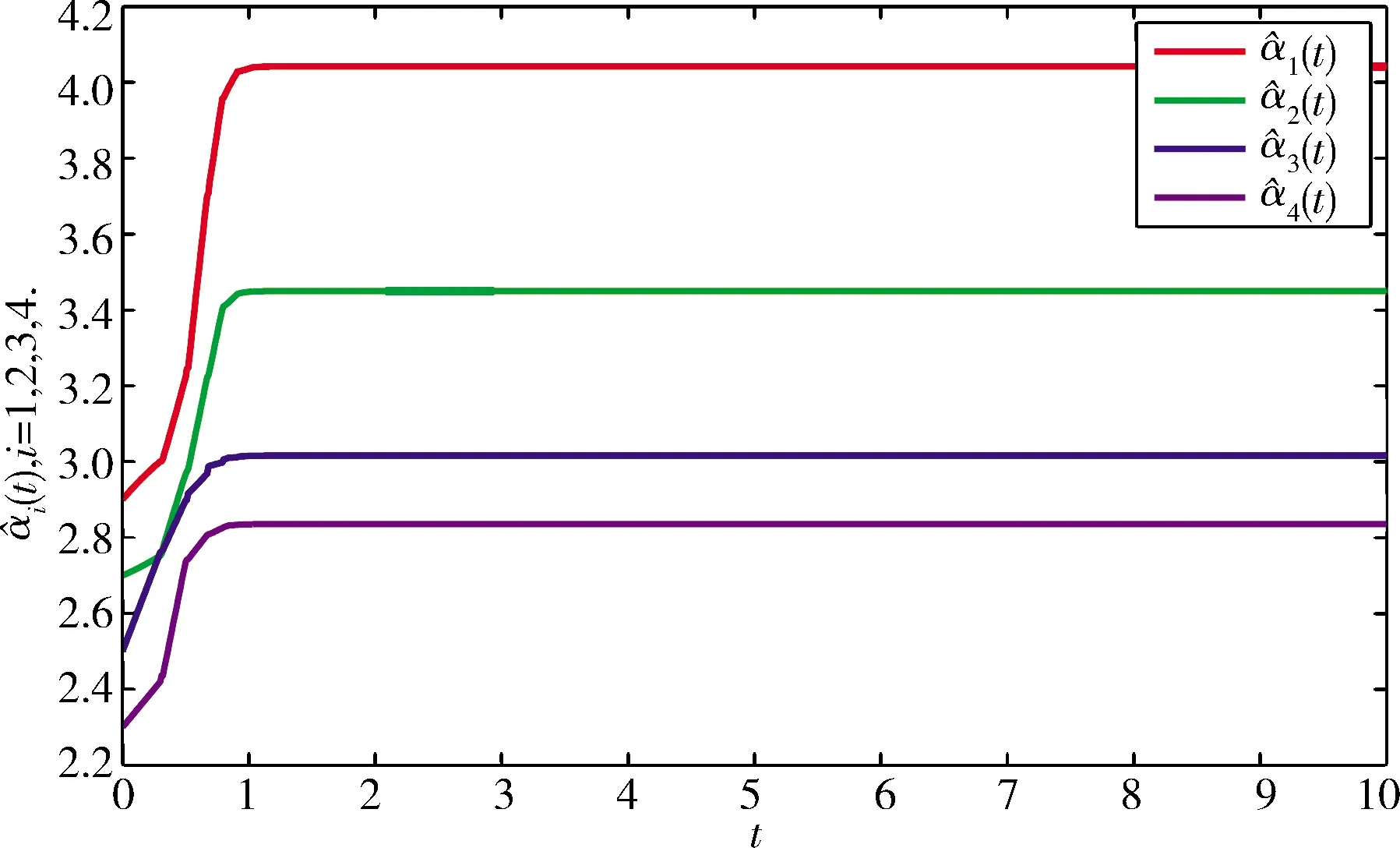
图 8 自适应触发参数

图9 自适应触发参数

4 结论

本文基于观测自适应事件触发控制方法,研究了具有一般线性动力学的主从多智能体系统的一致性问题,并利用Lyapunov稳定性理论和线性矩阵不等式技巧得到了主从多智能体系统达到一致的相关条件.

致谢天山创新团队项目(2020D14017)和天池博士项目(TCBS201803)对本文给予了资助，谨致谢意.