基于改进遗传算法的多目标柔性作业调度研究＊

李长云 谷鹏飞 林 多

（①智能信息感知及处理技术湖南省重点实验室，湖南 株洲 412000；②湖南工业大学轨道交通学院，湖南 株洲 412000）

近年来，在“中国制造2025”的背景下，智能化、信息化和现代化制造已经成为企业发展的重要趋势。如何使用科学且合理的生产调度方案来充分利用现有资源、如何合理组织生产过程来提高生产效率成为了企业关注的热点问题。然而，车间调度的不确定性和多约束性使得这一问题变得更加复杂，但它也更加符合实际的生产需求。

随着智能工业生产引起了越来越多的人的关注，国内外在柔性作业车间调度问题（flexible job-shop scheduling problem，FJSP）上也进行了多方面的研究，并且取得了一些成果。如：Luo R[1]等提出了一种改进的萤火虫算法（FA），用于数据驱动的工作车间调度系统中的特征选择优化调度。Liang X[2]等使用混合量子粒子群优化（QPSO）算法来解决灵活的作业车间。Jiang X[3]等提出了一种改进的PSO算法，基于前人利用随机规划知识建立的多目标随机调度模型，来优化RBF神经网络（IPSORBF）的函数逼近。Chen W[4]等建立了模糊FJSP的数学模型，提出了一种基于局部优化策略和改进优化旋转角度的混合量子算法。Wu P J[5]等建立了水处理方案的数学模型，结合车间的实际需求，设计了一种DLNN和遗传算法相结合的综合调度算法。桂林[6]等在现有的邻域结构的基础上进行拓展提出一种新型邻域结构。梁迪[7]等改进了狼群优化算法，并将其应用在了双车间调度问题上。陈魁[8]等提出了一种小生境粒子群优化算法。宋昌兴[9]等改进了多目标遗传算法。裴小兵[10]等提出了一种混合进化算法来解决流水车间调度问题。Phu-ang A[11]等提出了一种利用模糊选择机制的微分演化（DE）算法来解决灵活的工作车间调度问题（FJSP）。Khan B[12]等扩展了i-NSGA-III算法，以解决具有多个目标的制造工作车间调度问题。从国内外对于FJSP的相关研究现状来看，存在着如下几个问题：（1）使用的优化算法的寻优能力一般，主要是算法的反应时间太长，且容易进入局部最优解。（2）优化的目标过于单一，优化目标往往只考虑了最大完工时间，没有反应车间的实际生产情况。因此，针对车间生产过程中由于加工机器的加工时间分配不均导致的机器负载过大或者机器闲置等问题，本文提出了一种基于均衡化加工机器使用率的改进遗传算法，用来提高算法的搜索能力和稳定性。

1 柔性作业车间调度问题

1.1 柔性作业车间调度问题的描述

FJSP可以描述为有n个待加工工件（O1，O2，···，On）需要在m台机器上进行加工，每个工件需要经过Oij（Oij≥1）道工序，每道工序可以在任意一台机器上完成加工，同一道工序在选择不同的机器进行加工时，所需要的时间不同，所以在开始加工之前，需要确定每个工件的加工步骤以及各加工机器和工序加工的时间，因为在选择不同机器加工时，所有工序所需的处理时间不同，因此大大提高了调度的灵活性和复杂性。

本文提出的柔性车间调度问题是一个多目标静态灵活车间调度问题，不考虑机器突然故障、工人临时休假、订单突然取消、紧急工件插入以及忽略工序加工之间的转移时间。在以最小化最大完工时间为主要优化目标的条件下，均衡化各加工机器的利用率。最大完成时间是指在所有机器中完成时间最晚的机器的完成时间。

1.2 数学模型

数学模型中涉及到的参数如表1。

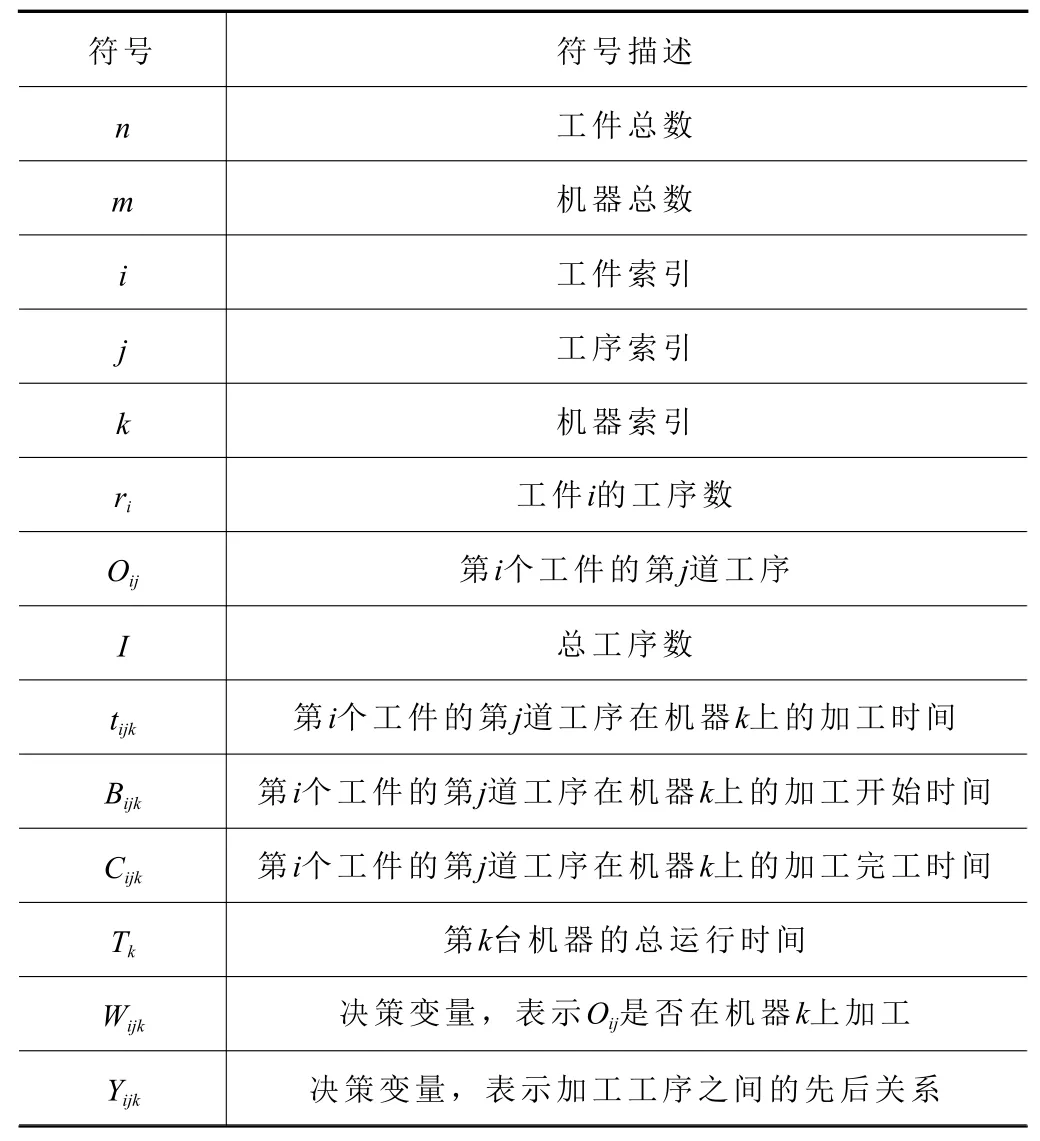
表1 模型参数表

对FJSP做以下假设：

（1）同一个工件中，相邻工序之间存在加工顺序约束，即后一道工序必须在前一道工序完成之后才能进行加工。

式中：Cij、Bi(j+1)分别代表工序Oij的加工完工时间和Oi(j+1)的加工开始时间。

（2）各道工序在同一时刻只能在一台机器上进行加工。

如果在某一时刻，Wijk=1，则不能同时出现另一个工序Ouv使得Wuvk=1。

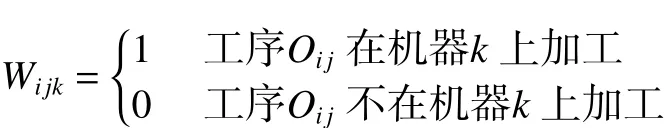
（3）任意工序一旦在某台机器上开始加工，则加工过程不能中断。

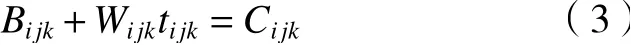
（4）每台机器在一段时间内只能加工一道工序。

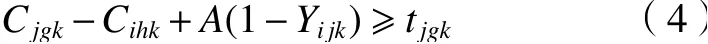
式中：A为一个较大的正数。

（5）各个工件在零时刻均可开始加工。

目标函数说明：

（1）最小化最大完工时间f1。

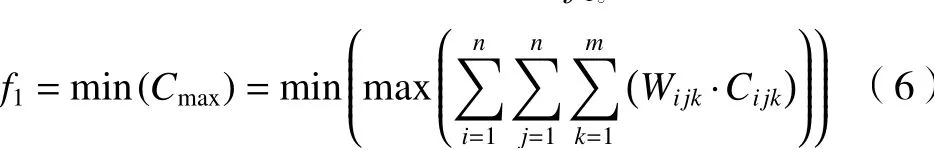
（2）均衡化机器利用率f2（各机器运行时间大致相同）。

式中：采用了标准差来计算各机器的使用时间，标准差越小，则代表各机器相应的运行时间就相差越小，因此求均衡化机器利用率等同于求解最小标准差。

综合目标评价函数f为

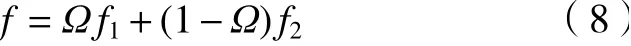
式中：Ω为随机给定数字，满足0<Ω<1。

2 改进遗传算法的实现

遗传算法（GA）是一种通用的启发式搜索算法。它是基于自然进化的自然选择和突变。在运用遗传算法进行FJSP求解时，先对种群进行初始化操作，种群中的每个个体都代表一种调度方案。以设定的目标函数为标准，通过选择、交叉、变异过程，更新种群的适应度，然后经过多次迭代，最终找到一个可行解。

2.1 算法流程

算法流程图如图1所示，首先初始化种群，对加工工件OS以及机器MS进行整数编码，将工件的工序、加工时间和机器数等信息存储在染色体中，然后对随机生成的种群进行解码，计算个体的适应度，结合轮盘赌选择和精英保留策略，将优秀的个体保留下来，再进行交叉和变异操作，最后判断是否达到迭代次数，将最优个体输出。

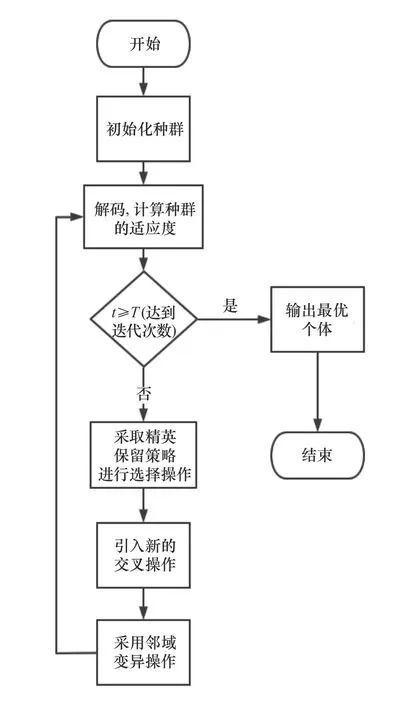
图1 FJSP算法流程图

具体步骤如下：

步骤一：设置参数、编码，随机生成一组初始种群。

步骤二：解码、计算种群的适应度值。

步骤三：采取精英保留策略，保留父代中的优秀染色体，然后使用轮盘赌选择算子进行选择操作，挑选优秀染色体。

步骤四：交叉操作，根据交叉概率，让父代染色体两两配对，采用POX交叉算子，得到子代染色体，提高种群多样性。

步骤五：变异操作，根据变异概率，使用基于邻域的变异算子。

步骤六：继续执行步骤二，直到迭代次数达到预定值，然后将种群中的最优个体输出。

2.2 种群初始化

编码方式采用单链整数编码，分别是基于工件OS和机器MS的编码，将编码分为3部分，第一部分的编码为工件，第二部分的编码为对应工件的加工机器，根据加工工件和加工机器，在第三部分编码上自动生成工件在对应机器上加工的时间，例如，对于一个包含3个工件的FJSP问题，如图2所示，第一部分工件加工顺序为13233121，编码中出现的第4个数字是3，它是出现的第二个3，所以它代表第三个工件的第二道工序；第二部分加工机器的编码为23312132，这一段编码中第7个数字是3，它代表第二个工件的第二道工序在第三台机器上加工。编码的最后一部分为加工时间，它在加工工件和加工机器生成后产生。根据种群大小随机生成工序码和机器码。

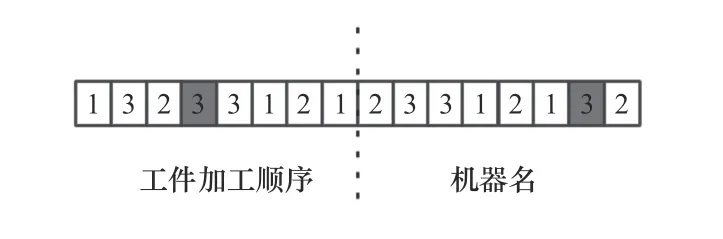
图2 染色体编码

2.3 解码及适应度计算

解码过程等同于编码的逆过程，同时遍历编码的3个部分，即可得到加工信息。本文求解的是多目标FJSP，基于上文的综合目标评价函数f，使用一个权重系数Ω将多目标问题转化为单目标问题。

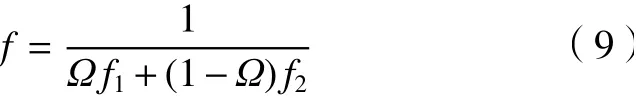
式（9）为式（8）的变形，适应度函数应该与优化方向相同，然而最小化最大完工时间及均衡化机器使用率均与优化方向相反，因此将之前所得的目标函数做倒数运算得到新的目标函数f。

2.4 选择操作

选择操作是选取具有高适应度的个体，如果选择操作符设计有问题的话，具有较大适应度值的个体就会使种群的进化方向单一，进而使种群丢失多样性，本文将遗传算法中的精英保留策略和轮盘赌相结合，使用轮盘赌挑选优质的染色体，适应度越高的染色体在种群中的适应度的占比就越高，如果种群的数量为n，个体的适应度值为fi，则个体的选择概率为Pi。

通过目标函数约束，得到最优解，同时采取精英保留策略，将父代种群中优秀的染色体放到子代种群中，不参与后面的交叉、变异操作，直到有更优的个体替换它，采用这种选择方式可避免优质解的丢失，加快种群的收敛[13]。

2.5 交叉操作

在遗传算法中，交叉是一个重要的操作，使用交叉算子能够将父代的优秀基因遗传给子代，本文使用了一种POX交叉算子对工件编码进行交叉操作，使种群的多样性更加丰富，步骤为：

（1）步骤一。随机取出两条染色体，分别作为父代F1和父代F2，然后建立两个空子集J1和J2，随机分配工件集｛1, 2, 3, ···,n｝到J1和J2中。

（2）步骤二。将父代F2包含在J1的工件复制到子代C2中，父代F1包含在J1的工件复制到子代C1中，保留它们的位置。

（3）步骤三。将父代F1包含在J2的工件复制到子代C1中，父代F2包含在J2的工件复制到子代C1中，保留它们的顺序。

本文以4个工件为例，图3表示了两条染色体F1和F2的交叉操作，父代F1和F2交叉生成了子代C1和C2，其中C1的染色体基因为[3 1 2 4 3 2 1 2 4 1 3 4],C2的染色体基因为[2 3 3 2 4 1 4 1 2 4 1 3]，从图3可以看出C1的染色体基因保留了F1中工件号为｛1，2｝和F2中工件号为｛3，4｝的次序，C2的染色体基因保留了F2中工件号为｛1，2｝和F1中工件号为｛3，4｝的次序，使子代能够继承父代的优良特征。

图3 POX交叉操作

2.6 变异操作

本文设计了一种改进的变异方法，针对工件编码采用基于邻域搜索的变异算子，它不会破坏种群的多样性，还能够提高子代的适应度，使其向更优的方向进化，针对机器编码采用单点变异法，替换可选机器。邻域搜索如图4所示，单点变异法的操作如图5所示。

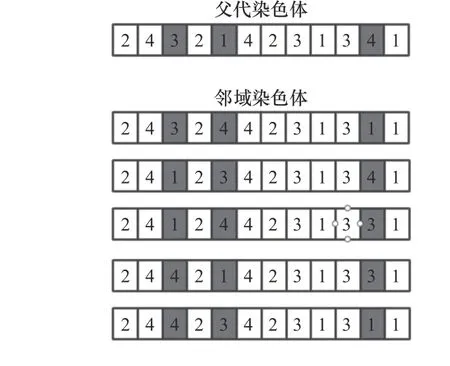
图4 基于领域搜索的变异操作

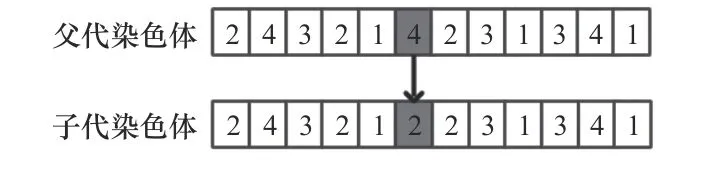
图5 单点变异操作

具体步骤如下：

（1）步骤一：首先随机选取种群规模乘上变异概率数量的子代个体。

（2）步骤二：取变异染色体上几个不同的基因，生成其排列的所有邻域，本文选取了3个不同位置的基因，进行邻域变换。

（3）步骤三：评价所有邻域的适应度值，找到最优的基因，然后让它取代原染色体基因。

3 仿真实验及分析

为了验证所提的改进GA算法在解决FJSP上的性能，本文选取kacem测试集[14]中的10×10FJSP，其中改进GA算法是在MATLAB语言上进行编写并调试，仿真实验是在计算机内存为4 GB，处理器为Intel(R) Core (TM) i5 4 200H，主频 2. 8 GHz、运行环境为Windows 10的个人计算机进行。实验参数设置如表2所示。

表2 实验参数

选择10×10的kacem算例，详细信息见表3。使用改进遗传算法和标准遗传算法以及帝王蝶优化算法（monarch mutterfly optimization，MBO）各进行仿真实验100次，以5次为1组取它们的平均值，得到平均值对比图如图6所示，通过图6可以直观地看出，在进行组内实验时，改进遗传算法相对其他优化算法更容易接近全局最优解。利用改进遗传算法进行仿真实验得到了FJSP甘特图如图7所示。

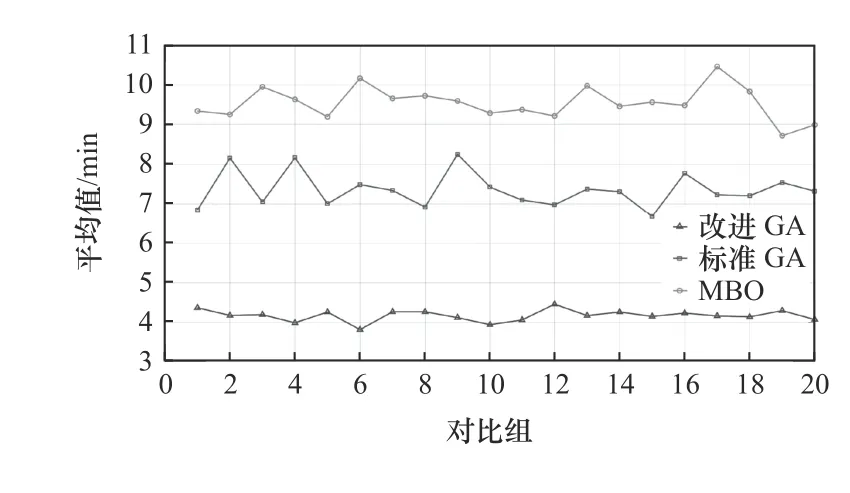
图6 平均值对比

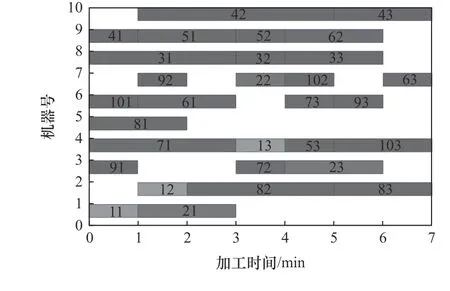
图7 10×10FJSP甘特图

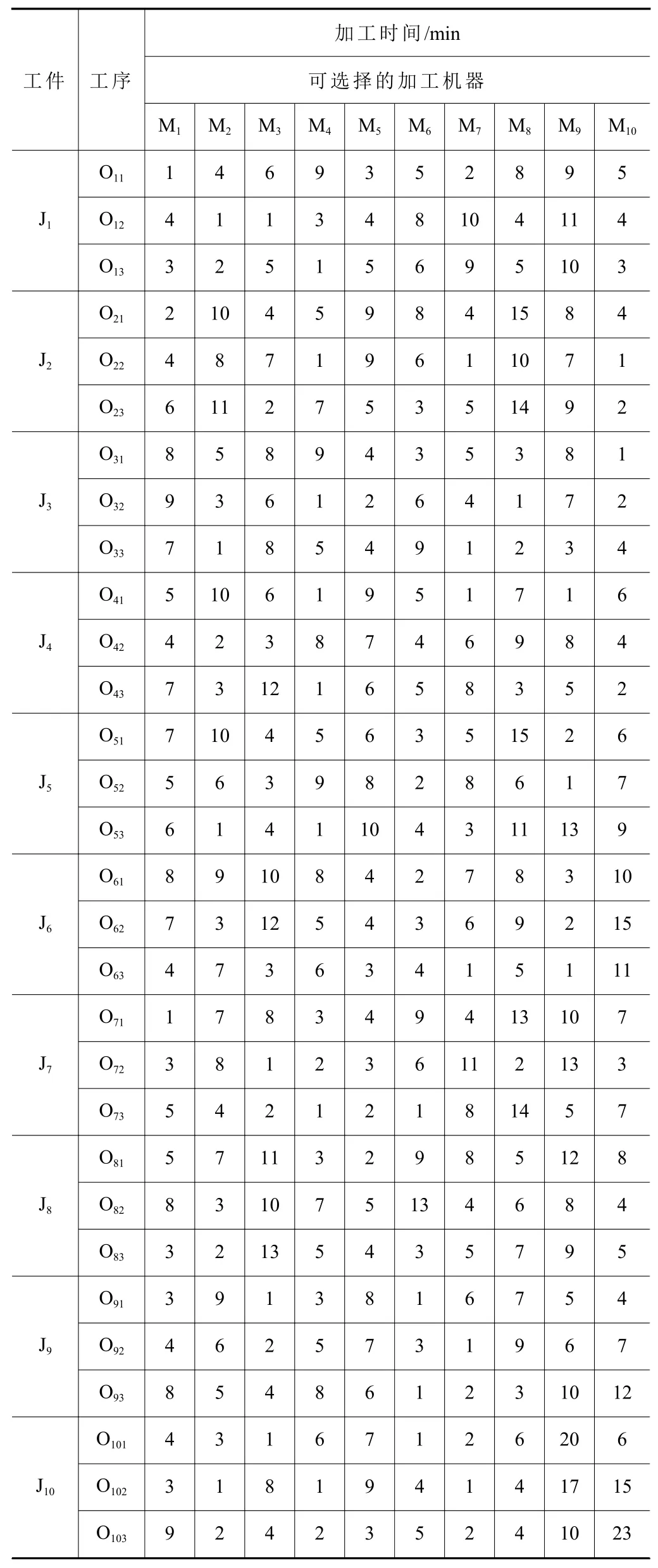
表3 10×10FJSP工件加工时间

基于最大完工时间以及均衡化机器利用率的各优化算法收敛曲线如图8所示，实线表示改进GA算法，点划线表示蝴蝶优化算法(MBO)，虚线表示GA算法，从收敛曲线上可以发现随着迭代次数的增加，改进GA算法在求解目标函数值的优化效果上明显优于其他两种算法，且相对于GA算法，改进GA算法收敛速度更快。

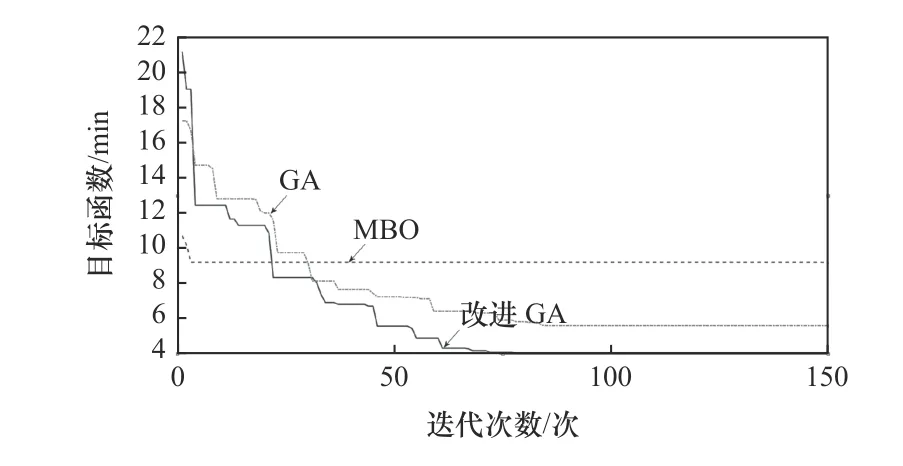
图8 收敛曲线比较图

4 结语

本文基于均衡化机器利用率以及最小化最大完工时间的多目标FJSP设计了一种改进遗传算法，对多目标进行优化求解，并通过在Kacem数据集上与其他优化算法进行对比，实验结果验证了改进遗传算法在求解多目标FJSP上具有更高的寻优效率和有效性。最后得到的实验结论如下。

（1）在进行染色体编码时，采用了单链整数编码，将工件号、机器号以及加工时间都放在一条染色体上，可以快速地计算适应度，提高了算法的求解效率。

（2）用标准差来表示均衡化加工机器的利用率，不仅符合了车间生产的实际情况，也提高了计算的精确度。

（3）采用了POX交叉算子和多点交叉法对工件编码及机器编码进行交叉操作，采用了基于邻域搜索的变异算子，避免算法过早地陷入局部最优解，从而扩大了寻优范围，增强了寻优能力。