基于工况叠加法的机翼压心位置确定技术

2022-05-12

现代机械 2022年2期

(中国飞行试验研究院，陕西西安 710089)

0 引言

固定翼飞机在飞行中机翼所受气动载荷的集中力作用点称为压力中心，简称压心，在设计阶段会由设计方通过风洞试验及仿真计算给出机翼压心的分布范围。压心位置随飞行参数变化而变化，通过确定压心的位置，可以初步确定机翼所受气动载荷在空间上的分布形式，分析压心位置的变化是分析飞机机动特性的重要一环，对飞机气动特性及静稳定性的评估有着重要意义，而通过在不同的机动中确定压心位置的变化形式，也可以确定机动过程中机翼所受气动载荷的特性[1]。

目前常用的确定压心位置的方法有两种：应变法和压力分布测量方法。应变法是通过载荷校准地面试验建立载荷方程，飞行中确定某剖面的剪力、弯矩及扭矩，再通过刚轴坐标等机翼结构参数获得压心的位置；压力分布测量方法可直接获得机翼上气动载荷的分布形式从而求得压心位置[2-3]。

应变法算得压心依赖于载荷方程，目前载荷标定技术所得剪力方程与弯矩方程精度较高，扭矩方程的精度有限，且应变法计算压心位置需要3个步骤，即将电桥响应数据转换为结构载荷，将结构载荷转换为气动载荷，由气动载荷算得压心，压心位置误差经三个过程累计放大，计算结果精度有限，在某些机动过程中当机翼气动载荷较小，误差影响放大，应变法算得压心远超机翼空间范围，该结果显然不合理；而压力分布测量方法要求环境条件复杂且维护成本较高，因此在多数飞机上无法使用[4]。

本文基于叠加原理提出工况叠加法计算压心位置，该方法通过建立地面工况数据与飞行数据之间的联系，由电桥响应直接计算压心位置，并分析了飞行机动段过程中的压心位置变化规律，对比了应变法与工况叠加法计算某大型民机机动平衡及滚转机动时的效果，结果证明工况叠加法有效、可靠[5]。

1 压心位置计算原理

1.1 应变法原理

应变法通过载荷校准地面试验建立载荷方程，表征电桥输出与结构载荷的关系，飞行中利用载荷方程反向推导结构载荷，载荷方程形式如下：

(1)

式中，Fi为广义剖面载荷向量；μ为电桥系数矩阵；β为应变电桥响应向量。

式(1)中Fi为地面停机状态清零后结构载荷变化量，扣除姿态角及过载对剖面结构载荷的影响之后，可获得飞机飞行状态下各剖面外所受气动载荷，利用剖面外所受气动剪力、弯矩及扭矩即可求得压心与剖面、刚轴的展向距离和弦向距离。

1.2 工况叠加法原理

由于校准试验工况受载方向均为法线方向，且机翼法向变形与其特征长度比值较小，满足各向同性假设及小变形假设，证明机翼结构为线弹性结构后，当各剖面电桥响应相等，即剖面局部应变相同时，由胡克定律可知，机翼剖面所受剪力、弯矩、扭矩相近，则机翼上的压心位置也相同。因此，工况叠加法的思路为将地面工况叠加为某虚拟工况，当该虚拟工况的剖面局部应变与空中状态点的局部应变相同时，可将虚拟工况的压心位置等效为对应状态点的压心位置。

基于叠加原理，建立地面工况与空中飞行时剖面电桥响应之间的关系，将飞行时机翼剖面的受载情况分解为地面工况的线性叠加，并通过最小二乘法求得各地面工况对应的拟合系数。拟合系数λ的物理意义为各地面工况对飞行状态的叠加权重，系数越大贡献度越高。

2 地面验证

以某大型民机机翼地面标定试验数据为基础，进行工况叠加法的地面验证分析。机翼结构如图1所示，该机翼结构为双梁结构，翼尖剖面在前梁、后梁与剖面交接处共布置有4个弯矩电桥，4个剪力电桥，并在蒙皮上布置了2个扭矩电桥，选用主桥进行地面验证。

由于载荷校准地面试验时通过液压作动器加载，因此可准确测量加载点位置，并通过不同加载点载荷算得等效压心位置。下文首先验证所选电桥的叠加原理，然后比较工况叠加法计算压心位置与真实压心位置，并给出误差结果。

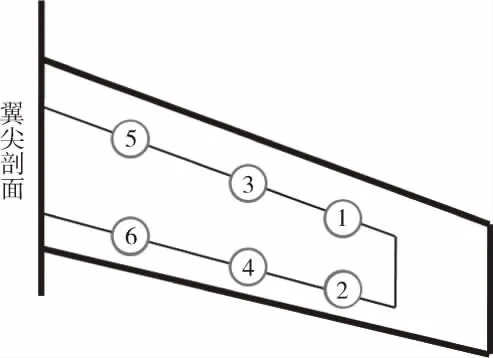
图1 右机翼翼尖剖面及加载点示意图

2.1 叠加原理验证

由图1可知，翼尖剖面外侧存在6个加载点，地面标定时分别对6个加载点单点加载，存在6个单点加载工况，工况编号与加载点编号一致。将6个工况的电桥响应叠加后，将叠加结果与6点协调加载时的电桥响应进行比较，如两者相差较小，即可视为电桥输出可线性叠加，结构满足叠加原理，验证结果如表1所示。

表1 叠加原理验证误差结果

表中对于工况叠加法选用5个电桥，其叠加原理验证误差均小于5%，满足叠加原理要求。

2.2 工况叠加法误差统计

基于地面标定试验数据，对工况叠加法计算结果进行误差分析，由上节可知存在6个单点加载工况，为防止地面工况与验证工况共用，出现自建自验问题，增加拟合误差的可信度，分别将3号工况及4号工况作为验证工况，并分别将剩余5个工况作为地面工况，首先计算压心与剖面之间的展向距离，误差统计结果如表2所示。

表2 工况叠加法展向压心位置误差

其次利用工况叠加法计算压心与刚轴之间的弦向距离，由于6个单点工况的压心均在前梁或后梁上，位置过于靠前或靠后，不符合机翼压心分布规律，因此补充一个多点协调加载工况7号工况，由3、4、5、6号点同时协调加载，压心位于翼尖剖面刚轴附近，误差统计结果如表3所示。

表3 工况叠加法弦向压心位置误差

由表2及表3可知，利用工况叠加法计算时，压心的展向距离和弦向距离绝对值误差都较小，但是由于压心与刚轴之间的弦向距离很小，因此压心弦向误差百分比较大，仍小于10%。

3 空中实测及对比

基于该大型民机横向机动及纵向机动时的应变数据、飞参数据(采样率均为8)，使用应变法与本文提出的工况叠加法分别计算压心距离，并结合飞参变化与理论分析对比两种计算方法所得结果。为防止计算贡献系数时地面工况之间产生冗余，降低最小二乘法计算误差，计算压心展向位置时，选用1、3、5号工况作为地面工况，计算压心弦向位置时，选用5、6号工况作为地面工况。

由于弯矩电桥和剪力电桥对弯矩和剪力较敏感，剪力电桥和扭矩电桥对扭矩较敏感，因此应变法计算压心位置时，剪力方程、弯矩方程及扭矩方程对应的电桥系数如表4。

表4 应变法各方程选用电桥及电桥系数

本章图中数据已脱密处理，且未标出飞参单位，应变法及工况叠加法算得压心位置单位为mm。

3.1 纵向机动

在高度为10000 ft(1 ft=0.3048 m)，空速为230 kn(1 kn=0.514 m/s)时执行纵向机动，升降舵初始状态为下偏，随着升降舵偏度逐渐转为零偏，飞机开始做纵向机动，俯仰角开始由正值逐渐转为零值，而滚转角始终不变，飞参及两种计算方法所得压心展向距离如图2所示(压心距离单位为mm)。

图2 纵向机动时两种方法算得压心展向位置对比

由于飞机滚转角未在机动中发生变化，飞机的纵向机动中未掺杂横向机动，因此机翼压心在展向方向上不应产生过大移动，工况叠加法计算结果较为合理，而应变法计算所得压心展向距离随升降舵偏度变化而变化。

飞参变化及两种计算方法所得压心弦向距离变化如图3所示(压心距离单位为mm)。

图3 纵向机动时两种方法算得压心弦向位置对比

由相关理论可知，随着飞机姿态角及迎角发生变化，升力沿飞机弦向的分布也发生变化，图3中随着俯仰角降低，压心向后缘移动，因此应变法与工况叠加法所求得压心位置沿弦向变化规律符合预测，且由图2及图3中数据可发现明显的迟滞现象，在飞机活动面产生偏度之后2～3个数据点之后飞机姿态角开始变化，随后机翼压心的空间位置开始变化。

3.2 横向机动

在高度为30000 ft(1 ft=0.3048 m)，马赫数为0.7时执行横向机动，初始状态左副翼向上满偏右副翼向下满偏，飞机向左侧滚转，当滚转角达到-45°时，副翼偏度迅速变化，飞机做横向机动，转为向右侧滚转，机动过程中俯仰角变化约2°，飞参及两种计算方法所得压心展向距离变化如图4所示(压心距离单位为mm)。

图4 横向机动时两种方法算得压心展向位置对比

由图4可知，两种计算方法算得结果趋势相似，当飞机副翼偏度不变时，滚转角匀速变化，机翼上压心的展向分布变化较小；当飞机作横向机动，右副翼从向下满偏迅速转为向上满偏的瞬间，副翼提供升力迅速降低，由于副翼在剖面外侧紧靠剖面的位置，因此在副翼偏转瞬间，副翼外侧的机翼提供更多升力，压心朝翼尖方向迅速移动；随后右副翼偏度由向上满偏逐步降低，飞机滚转角减小，翼尖剖面外侧机翼上升力重新分布，压心向翼根方向移动。由图4可知，由于过载传感器安装位置限制，机动过程中结构振动导致过载传感器局部过载不稳定，应变法算得结果抖动明显，而工况叠加法直接建立应变之间的关系，避免了传感器引起的误差。

飞参及两种计算方法所得压心弦向距离变化如图5所示(压心距离单位为mm)。由于副翼下偏为正，机动瞬间左副翼向上满偏迅速转为下偏，右副翼由向下满偏迅速转为上偏，右副翼上偏后由副翼提供的升力突然降低，机翼分配升力增加，因此压心应向航前方向移动，即压心弦向距离增加，由图5可知，应变法与工况叠加法算得结果与理论预期相符合。

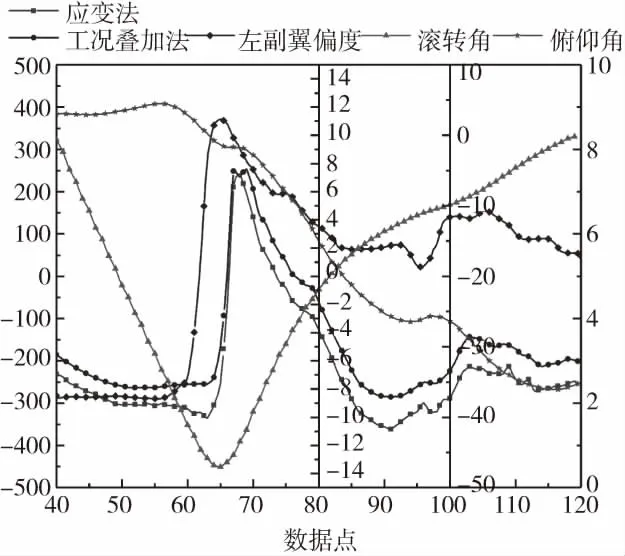
图5 横向机动时两种方法算得压心弦向位置对比

3.3 小过载推杆机动

在高度为10000 ft(1 ft=0.3048 m)，空速为230 kn(1 kn=0.514 m/s)时驾驶员推杆，进行小过载推杆机动，飞参及两种计算方法所得压心展向及弦向距离如图6、图7所示(压心距离单位为m)。

由图6、图7可知，驾驶员做推杆机动，法向过载降低，图中法向过载接近零时应变法计算所得压心的展向及弦向位置远超机翼特征长度。由应变法原理可知，当飞机所受气动载荷接近零，应变法计算过程中载荷误差被放大导致压心位置误差极大，算得结果明显不合理，工况叠加法通过直接建立电桥之间的关系，避免了由气动载荷接近零带来的误差。