V型轮在输电线路机器人的应用研究*

(江苏省送变电有限公司，江苏 南京 211102)

0 引言

近年来，随着我国经济的飞速发展，架空输电线路规模迅速扩大，平均每年以不低于4%的速度增加。根据《中国电力年鉴》，截止2017年底全国高压架空输电线路总里程已超过180万公里。受限于专业技术工人队伍成长缓慢，结构性缺员情况日益严重，架空输电线路建设、运行、维护、检修等工作向智能化、自动化转型需求迫切。

现有的架空线路新型设备中，输电线路机器人以其适应性强、出勤率高、工作质量稳定、成本低，具有广阔的发展前景。输电线路机器人能在输电线路上自主地行走、跨越障碍，通过携带的视觉系统、导航系统、智能分析处理系统、作业系统等设备，可以完成或辅助人工完成线路的安装、巡视、检修等工作，且不受地形地锚、气候条件、空中管制等因素影响，工作质量稳定[1-5]。

基于导地线行走的输电线路机器人，由于相邻杆塔地面高程、塔高以及导地线弛度因素的影响，机器人在工作过程中，始终处于有一定坡度的行走路径上，因此爬坡性能是其关键的性能指标。本文从线路飞车上V型行走轮多年的应用经验出发，根据机械传动中V型带轮的设计原理，研究V型轮槽的行走轮在线上行走的力学特性，分析得出其最优设计参数，使机器人获得最佳的运动性能，提升机器人性能指标、降低功耗。

1 V型轮在输电线路机器应用的结构设计

输电线路机器人使用的V型轮是指轮槽底为V型或等腰梯形的驱动轮，考虑线上行走的轮外径的尺寸不宜过大，通常采用等腰梯形设计。该等腰梯形的底边和斜边长根据行走的导地线线径确定，其斜边的斜角最优值受不同材质的摩擦系数影响。

全尺寸的V型轮设计，在机器人沿弯轨道的导地线过桥引导杆行走时，引导杆和V型轮之间的摩擦力偏于一侧的V型斜边，致使V型轮在此处的V型轮斜边爬升，从而引发脱轮，机器人有坠落的危险。因此，全尺寸V型轮槽的设计不利于机器人线上行走平稳地过弯，鉴于此种原因，行走轮的设计可采用V型+2R型相结合的型式，详见图1。

图1 组合型行走轮结构

图2 组合型行走轮模型图

V型+2R型轮槽设计在正常行走时，V型槽底可以对导地线产生更大静摩擦力，给机器人提供更好的驱动力；在碰到障碍时，通过两种不同半径的圆弧形轮槽碾压障碍物，使过障碍更加平顺；同时，较大半径的圆弧形轮槽径R1，可以获得较大的槽顶开口而不必增大槽深，使机器人跨越障碍后落线准确度更高。

该型行走轮通常采用铝合金材质包胶或使用复合材料，兼顾摩擦力、耐磨性和轻量化。实物模型如图2。

2 V型轮在输电线路导地线行走的力学分析

2.1 刚体受力模型

V型轮在导地线上行走时，忽略其微小的弹性变形，将轮和导地线均认为是刚体，由此确定其受力模型，如图3。

图3 行走轮受力模型

V型轮在导地线上受到竖直向下的重力G，由于动力矩M的作用在两个接触点分别受两组沿前进方向静摩擦力f、垂直于V型轮斜边向上的支撑力N。

在轮子沿导地线匀速运动时，根据力平衡原理：

此时，∑X=0，∑Y=0，∑Z=0。

由图3可以明显看出，轮子受向前的静摩擦力f，而无反向的阻力，在X轴方向上受力不平衡。只有在动力矩M为0时，静摩擦力f消失，此时轮子才可匀速向前运动。

在无动力的情况下，轮子能匀速前进，此种情况显然与实际情况不符。因此，我们根据实际情况引入弹性变形情况进行修正。

2.2 圆形轮槽弹性变形状态受力模型

在实际情况下，由于轮子和导地线均不是理想的刚体，因此在接触时受到约束力影响，二者会产生弹性变形。在此情况下，二者的接触非点接触而是面接触。因此，其受力模型如图4。

图4 弹性变形状态驱动轮受力模型

在轮子静止或匀速运动的情况下，作用于轮子的主动力矩为M，产生一个对轮子的作用反力T，从而达到力偶平衡。此反作用力T可以等效为作用在点B，则B点必定在A点的前进方向侧，AB距离δ由轮子弹性形变产生[6-8]。将T沿x、y轴分解为沿前

进方向的静摩擦驱动力f和竖直支撑力N，根据力偶平衡：

N×δ+f×r′-M=0

(1)

由于轮子变形较小，可近似认为r′与轮半径R相等，整理式(1)得：

(2)

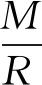
2.3 V型轮槽弹性变形状态受力模型

V型轮槽的行走轮在导地线上匀速行走时，其等效作用点为一对位于V型轮斜边上的点，此时的支撑力N垂直于V型轮斜边向上。

V型轮槽的行走轮不同于圆形轮槽行走轮，当其在线上匀速行走时，假设此时只受支撑力N，那么N=G/sinα，α趋于0°时N趋于∞，显然与实际情况不符。在实际情况下，两块竖直的板夹住圆柱体，因压力产生静摩擦力平衡重力作用，压力N不会趋于∞。由此，修正力系，此时V型轮受到重力G、支撑力N以及沿斜面向上的静摩擦力f。因此，导地线夹在其两个斜边中间，因轮产生弹性形变，当轮转动导地线自两斜边间脱开时，必然产生相对滑动，此时产生向下的滑动摩擦力。由于自等效作用点B向后方支撑力N逐渐减小，而AB之间距离极其微小，因此也可近似认为该滑动摩擦力等效作用在B点。

V型轮槽受力模型如图5。

由于图5中B点和B’点受力情况相同，取B点

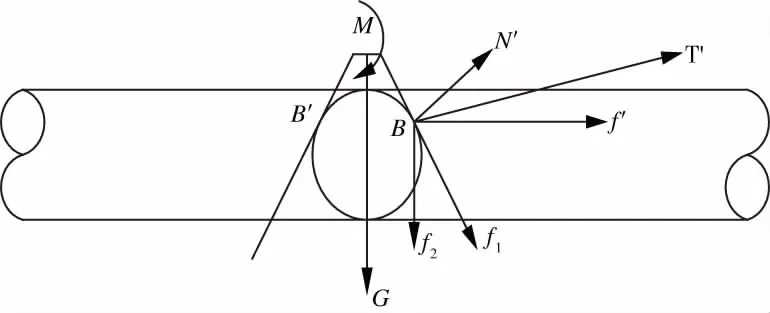
图5 机器人行走轮弹性变形状态受力模型

进行分析：作用于轮子的主动力矩为M、重力为G(在B点等效为M/2和G/2)，产生一个作用反力T’，此力分解为沿前进方向的分力f’和垂直于轮槽斜面的支撑力N’，轮转动产生沿斜面向下的动摩擦力f1，其竖直方向分力为f2，设V型轮斜边斜角为α，结合图2中模型，根据力偶平衡有：

(3)

设f’和T’夹角为ψ，f′=T′×cosψ；根据摩擦力公式，动摩擦力f2=f1×cosα=N′×μ×cosα，μ为动摩擦系数。代入公式(3)整理得：

(4)

由于轮子变形较小，可近似认为r′与轮半径R相等，应用三角函数公式整理得：

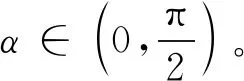
(5)

(6)

对比公式(2)圆形轮槽的驱动力f，则有：

f合max>f

(7)

所以可以得出结论：

1)在同等驱动转矩情况下，V型轮槽的行走轮比圆形轮槽的行走轮可以获得更大的驱动力，具有更好的行走效果。

导地线的外层材料为铝，考虑各种行走轮材质和铝的摩擦系数，V型轮槽斜边倾角最优值应在30°～45°之间。

3 结束语

本文通过力学分析，为V型轮在输电线路机器人中应用提供理论依据，在V型轮的参数设计和材料选择上有参考价值。由上文的结论可知，V型轮最佳驱动效果的斜边倾角与摩擦系数有关，在输电线路机器人的应用中可以合理选择材料和倾角，从而获得最佳的行走效果，能够有效的增加机器人的续航里程、爬坡能力、克服风偏和覆冰的影响。

V型轮结构在机械传动的带轮设计中有着广泛的应用，实践证明其有着优异的性能。在输电线路检修的应用中，部分飞车厂家通过产品的实践验证，V型轮结构比传统的圆形轮槽结构具有更好的驱动效果，对克服挂线点高差以及导地线弛度引起的坡度有着良好的效果。