电场调控的碳纳米管非线性光学开关及其管径效应

贺慧敏, 杨 辉, 李 莹, 李祥辉, 李志儒

(1. 太原师范学院 物理系 计算和应用物理研究所, 晋中 030619;2. 山西大同大学 炭材料研究所, 大同 037009; 3. 吉林大学 理论化学研究所, 长春 130023； 4. 福建师范大学 医学光电科学与技术教育部重点实验室 福建省光子技术重点实验室, 福州 350007)

1 引 言

随着光电技术的飞速发展, 非线性光学材料引起了科学界的广泛关注. 高性能非线性光学材料的设计与合成已经成为电信、光信息处理、光交换机、三维光数据存储、光限流等领域发展的重要课题[1-7].为了获得更多高性能的非线性光学材料, 最近几十年研究者们陆续提出了多种的措施去增强分子的非线性光学响应[8, 9],其中分子内长程电荷转移就是一种非常有效的策略, 被广泛应用于各种材料的设计[10-12].

纳米管自首次发现[13]以来, 已经成为理论物理、应用物理、化学和材料科学领域最热门的研究对象之一. 由于碳纳米管(Carbon Nanotube, CNT) sp2杂化骨架表面的大π键, 使其具有了优异的力学稳定性、耐化学性、导电性和导热性[14-21]. 基于大π键电子云的易极化和易流动的性质, 碳纳米管显示了良好的光学性能, 因此已经被广泛运用于非线性光学材料的设计和合成.例如, Xu等人通过掺杂硼/氮化片段设计并研究了硼/氮化片段的异质纳米管(BNCNTs)模型, 结果表明BNCNTs模型的非线性光学性质极大地依赖于C片段与BN片段的连接方式和组成比例.[22, 23]Li等人研究了带有Stone-Thrower-Wales (STW)缺陷的锯齿形纳米管, 发现增加管长和管径可以有效增强其二阶非线性光学响应[24]. Chen等人通过引入三角形BN纳米点对碳纳米管体系进行了边缘修饰, 研究发现这种修饰可以有效地提高该材料的第一超极化率(β0)[25].

鉴于碳纳米管独特的电子云特征, 我们能不能找到一种不同于上述化学方法的, 有效的策略来增强碳纳米管稳定性的同时也增强非线性光学响应呢? 最近的研究表明定向外电场的物理方法可以有效打破中心对称分子电子云的对称性, 发生分子内电荷转移, 从而带来大的非线性光学响应.[26-31]除此之外，夏明霞等在外加电场作用下研究了碳纳米管的结构稳定性以及对碳纳米管结构进行修饰，研究表明经过局部修饰后形成的碳纳米管在外电场的作用下形成了电子输运的势垒，从而拓展了纳米管的应用.[32]本文选取了五种具有不同管径的扶手椅形单壁碳纳米管 (Single-Walled Carbon Nanotube, SWCNT), 即CNT(3, 3)、CNT(4, 3)、CNT(5, 3)、CNT(6, 3) 和CNT(7, 3), 并将外电场施加于沿管长的方向, 使用密度泛函理论得到了不同外电场下各个碳纳米管的最优几何结构. 研究结果表明：外电场引起了碳纳米管分子内部明显的电荷转移, 因此大大增强了碳纳米管的非线性光学响应. 特别指出的是, 外电场对不同管径碳纳米管显示了不同程度的非线性光学响应急剧增大, 形成了电场调控的非线性光学开关, 可称为灵敏、快速、可逆的“电子结构异构化非线性光学开关”.

2 计算方法

B3LYP方法[33, 34]已经被成功地用于碳纳米管的几何优化计算[22, 25, 27]. 因此, 本文在B3LYP/6-31G*水平下, 优化得到了五个碳纳米管在不同外电场下的最优几何结构和振动频率, 并计算了体系的垂直电离能(Vertical Ionization Energy, VIE). 为了深入了解外电场作用下各个碳纳米管内部电荷转移的变化, 在相同计算水平计算了研究体系在不同电场下的自然布局分析(Natural Population Analysis, NPA)电荷. 此外, 为展示体系的非线性光学响应变化, 我们在B3LYP/6-31+G*水平计算了各个碳纳米管在不同外电场强度下的第一超极化率(β0). 第一超极化率β0的定义如下：

(1)

所有计算均采用Gaussian 09 程序[35]完成, 碳纳米管的几何结构图和最高占据分子轨道(HOMO)图由 Gauss View 5.0 程序[36]生成.

3 结果与讨论

3.1 几何结构和稳定性

图1 给出了五种不同直径的碳纳米管具有全实频的最优几何结构. 表1列出了相关的结构参数. 从表1可以清楚地看出, 在外电场作用下, 对于相同的碳纳米管, 管长和管径随着外电场的增强略微增大. 具体说来, 当电场从0 au增加到200×10-4au, CNT(3, 3)管长和管径分别增加了0.026和0.043 Å, CNT(4, 3)管长和管径分别增加了0.020和0.045 Å; CNT(5, 3)管长和管径分别增加了0.014和0.045 Å; CNT(6, 3)管长和管径分别增加了0.022和0.113 Å; CNT(7, 3)管长和管径分别增加了0.009和0.066 Å, 增加幅度均小于2.3%.显然, 外电场对五种不同管径碳纳米管的几何结构的影响很小.

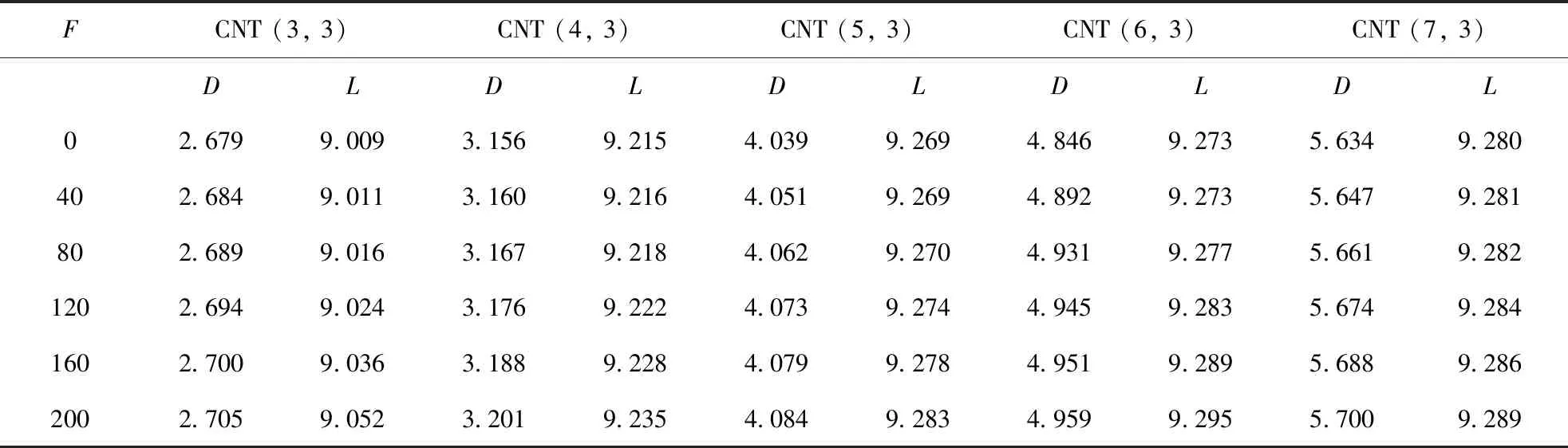
表1 不同管径的碳纳米管中涉及到的几何参数随外电场的变化

图1 不同管径碳纳米管的优化几何结构Fig. 1 Optimized structures of the different diameter carbon nanotubes.

为了评估碳纳米管在外电场作用下的稳定性, 我们计算了它们的垂直电离能(VIE)和最高占据轨道(HOMO)与最低未占据轨道(HUMO)的能量差, 即HOMO-LUMO能隙值. 外电场作用下的VIE和能隙值的具体数据列于表S1. 从表S1中可以看到外电场作用下碳纳米管的VIE的范围是3.85-6.97 eV, 与之前已报道的一些非线性光学分子的VIE相当[37-40]. 同时, 从表S1中可以看出能隙值的范围是0.44-2.20eV, 不同管径碳纳米管的能隙值差别较大. 图2展示了各碳纳米管的VIE和能隙值随外电场增大的演变. 从图2中可以看出对于CNT(3, 3)和CNT(4, 3)来说, 它们的VIE和能隙值几乎不随外电场的变化而变化. 而对于CNT(5, 3)、CNT(6, 3) 和CNT(7, 3)来说, 它们的VIE值和能隙值随着外电场的增大而增大. 特别是CNT(6, 3)的能隙值受电场影响较大, 在200×10-4au电场作用下从0.44增大到1.45 eV, 接近于实验合成的C60分子的能隙值(1.57 eV)[41]. 综上所述, 碳纳米管在外电场中具有较高的稳定性, 甚至随外电场增大而提高.

图2 不同管径碳纳米管的HOMO-LUMO能隙值和垂直电离能(VIE)随外电场增加的演变Fig.2 Evolutions of HOMO-LUMO gap value and vertical ionization energy (VIE) of different diameter carbon nanotubes with increasing external electric field strength F.

3.2 外电场作用下碳纳米管分子内部的电荷分布演化

图3给出了不同直径碳纳米管的最高占据轨道(HOMO)随外电场强度增加的演化. 从图中可以看出, 电子云沿着外电场的反方向进行了长程转移. 外电场作用下, CNT(3, 3)和CNT(4, 3)的电子长程转移不太明显, 这也是它们的VIE和HOMO-LUMO 能隙值几乎不随电场改变的主要原因. 而对于CNT(5, 3)、CNT(6, 3) 和CNT(7, 3)来说, 电子在外电场作用下发生了非常明显的长程转移. 特别是CNT(6, 3), 当F= 80 ×10-4au时, 电子云从碳纳米管左侧向右侧集中,这导致了CNT(6, 3)在此电场下HOMO-LUMO 能隙值的突然增大, 同时也许导致此电场下CNT(6, 3)第一超极化率的急剧增大. 另一方面, 为了更深入的分析电子云在外电场作用下的分布, 我们也进行了电荷的自然布局分析. 图4很清楚地展示了CNT(6, 3)的电荷分布随外电场的演变情况. 其它碳纳米管的电荷演变图在支持信息图S1-S4中. 由于这些碳纳米管的电荷分布随外电场的变化非常相似, 本文仅以CNT(6, 3)为例进行讨论和分析. 为了研究的方便, 我们把纳米管分为A、B、C、D四部分. 从图4中可以看出, A和D部分的正电荷随着外电场的增强而增大, 同时B和C部分的负电荷随着外电场的增强而增大, 这充分的说明了在外电场的作用下, 电子沿着与电场相反的方向进行了长程转移. 此外, 通过比较B和C两部分的负电荷, 也可以看出负电荷集中于C部分, 这导致了碳纳米管具有了大的电子云梯度, 产生大的非线性光学响应.

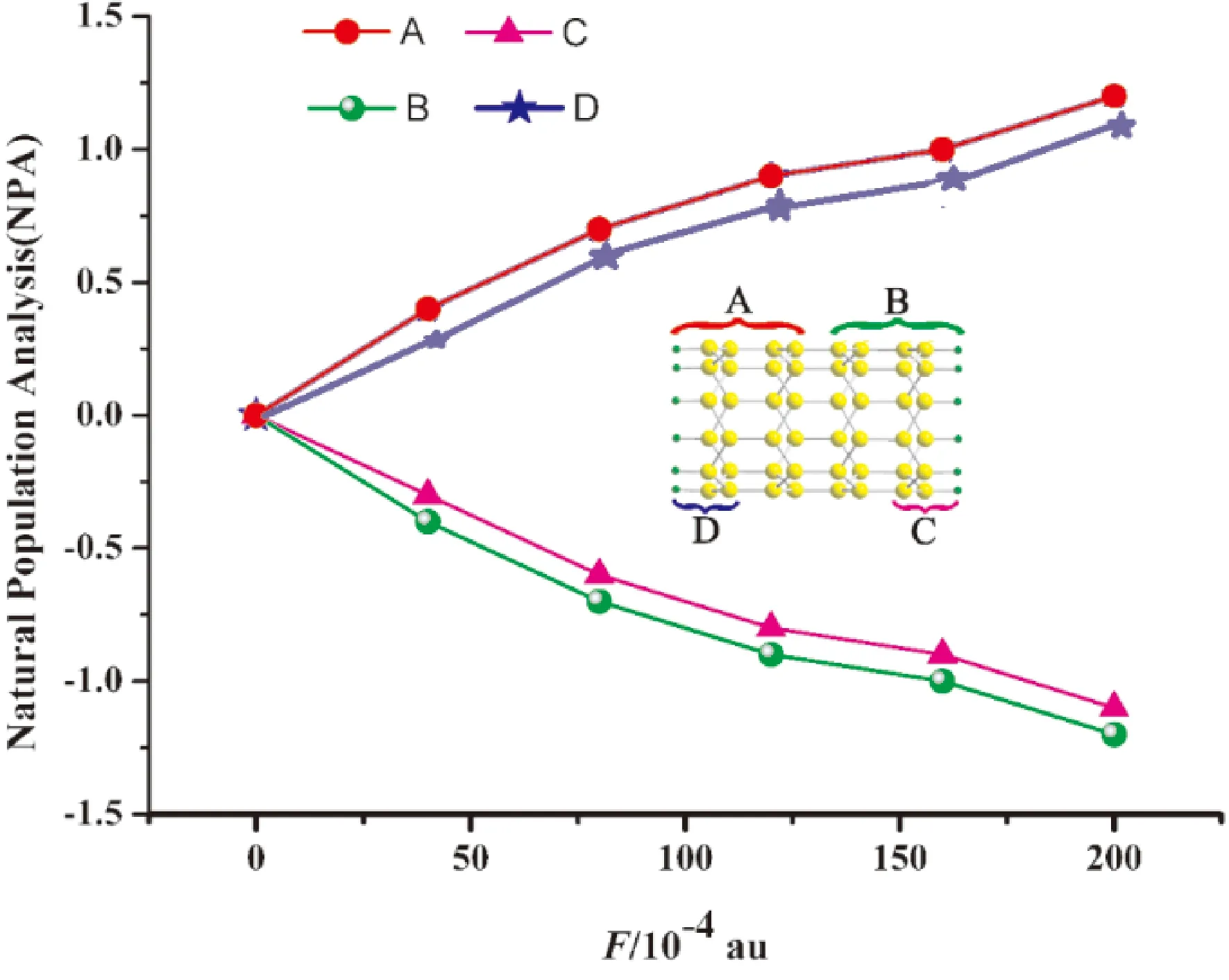
图4 不同外电场强度下CNT(6, 3)中各部分的NPA电荷Fig.4 NPA charges of CNT(6, 3) with different external electric field strengths.

3.3 外电场作用下碳纳米管非线性光学性质的演变

我们先前的研究表明, 外电场驱动的分子内的电荷远程转移在非线性光学研究中起着重要的作用[42]. 因此, 本文计算了各个碳纳米管在不同外电场下的第一超极化率β0(F). 表2给出了不同管径的碳纳米管在电场强度0～200 ×10-4au下的β0(F). 从表2和图5中可以看出在没有外电场时, 各个碳纳米管的二阶非线性光学响应是非常小的, 几乎没有非线性光学响应. 然而, 当施加逐步增大的外电场时,β0(F)值随之提高. 如上所述, 这主要是由外电场导致的分子内电荷转移并产生大的电子云梯度引起的. 图5a表明, CNT(3, 3)、CNT(4, 3)和CNT(5, 3)的β0(F) 随着所施加外电场的增大而逐步递增, 而且管径越大的碳纳米管的β0(F)受电场的影响更大. 该现象与图3中碳纳米管的HOMO轨道随电场的演变是吻合的, 即管径越大的碳纳米管HOMO轨道中电子云受电场的影响越大. 与此不同的是, 对于CNT(6, 3)和CNT(7, 3)来说, 他们的β0(F)在所研究的电场范围内分别出现了一个峰值. 图5(b)表明CNT(6, 3)在F= 80 × 10-4au时具有最大β0(F)值34873 au, 而CNT(7, 3) 在F= 160 × 10-4au时具有最大的β0(F) 值29426 au. 这与图3中CNT(6, 3)和CNT(7, 3)的HOMO轨道随电场演变的关系也是一致的, 即CNT(6, 3)和CNT(7, 3)的HOMO轨道的电子在F分别为80 × 10-4au和160 × 10-4au时已经都从左侧转移到了右侧, 导致了在这两个电场下的CNT(6, 3)和CNT(7, 3)分别具有最大的非线性光学响应.

我们以前的研究发现可以通过外电场调控非线性光学响应, 使其产生极大的β0对照, 从而得到新的非线性光学开关. 对于碳纳米管而言, 以CNT(6, 3)为例, 当不施加外电场时的β0(F) = 23 au, 但当F= 80 × 10-4au时β0(F)却高达34873 au, 因此外电场带来了一个非常大的β0(F)对比值. 那么, 我们把F= 0 au的状态定义为非线性光学开关的“关”, 相对应的把F= 80 × 10-4au的状态定义为非线性光学开关的“开”. 因此, 碳纳米管CNT(6, 3)非线性光学分子开关以Fw= 80 × 10-4au为工作电场. 同理，其他管径的碳纳米管也是非线性光学开关, 其中碳纳米管CNT(7, 3)的工作电场Fw为160 × 10-4au, 而CNT(3, 3)、CNT(4, 3)和CNT(5, 3)的工作电场Fw可选为200 × 10-4au，这些结果显示了非线性光学开关的管径效应. 需要特别关注的是, 本文提出的非线性光学开关是通过电场调控碳纳米管的电荷转移而实现的, 可称之为“电子结构异构化开关”. 这与之前文献里报道的基于调控PH值或者氧化还原等化学变化机制[43-47]而设计的非线性光学开关不同. 显然, 我们提出的这种非线性光学开关具有灵敏、快速、可逆等优点.

表2 外电场对碳纳米管静态第一超极化率β0(F)的影响

此外, 为了更好的分析和理解在各自工作电场下各个碳纳米管的不同非线性光学性质.我们也计算了工作电场下各个碳纳米管的电子跃迁性质, 包括跃迁能(ΔE)、振子强度(f0)、以及最主要的跃迁, 并列于表3之中. 表3表明ΔE是决定β0(Fw)大小的主要因素, 这与双能级公式[48, 49]描述的一样. 例如, CNT(5, 3)在其工作电场Fw= 200 × 10-4au下, 具有1.3861 eV的最小ΔE, 因此具有最大β0(Fw) 值83695 au.

对于非线性光学材料来说, 电子吸收光谱的透明区被看作是其工作区. 工作区对于非线性光学材料的实际应用来说是非常重要的. 图7展示了不同管径碳纳米管的电子吸收光谱.从图中可以看出, 这些碳纳米管的主要吸收区是在300-2000 nm, 而在小于300 nm和大于2000 nm波段是透明区. 因此, 本文研究的这些碳纳米管可以作为紫外兼红外非线性光学开关的候选物.

图5 碳纳米管的第一超极化率随外电场增加的演化Fig.5 Evolutions of β0(F) of different diameter carbon nanotubes with increasing external electric field strength.

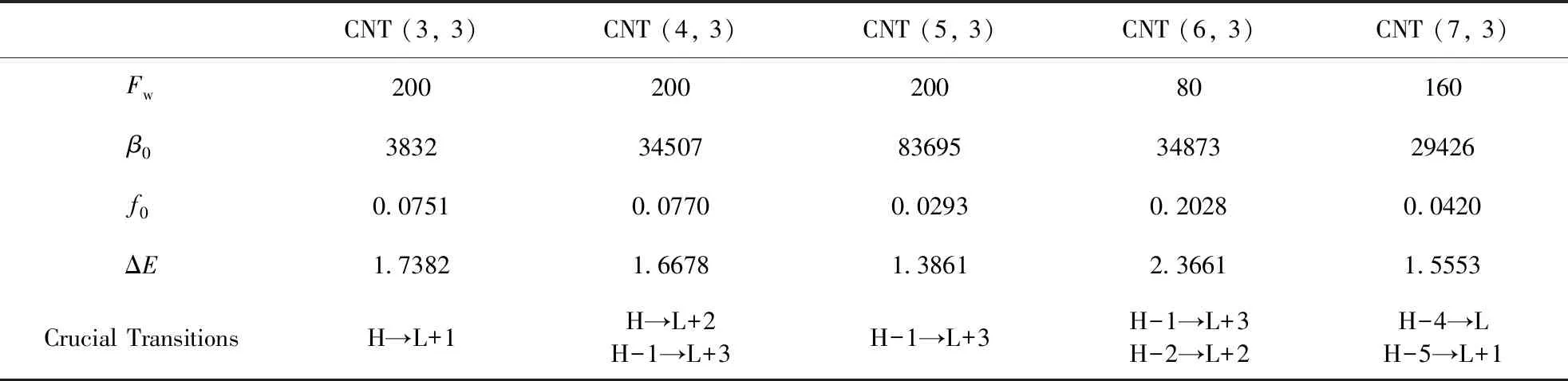
表3 所有碳纳米管的工作电场(Fw, 10-4 au)，静态第一超极化率(β0 (Fw), au)和相对应的跃迁能(ΔE)，振子强度(f 0)，以及最主要的跃迁轨道.

图7 不同管径碳纳米管的电子吸收光谱Fig. 7 Electronic absorption spectra of different diameter carbon nanotubes.

4 结 论

本文在B3LYP/6-31g*水平获得了五个不同管径碳纳米管的最优几何结构, 并且系统研究了外电场对它们的几何结构与电子性质的影响. 研究结果表明外电场对这些碳纳米管的几何结构的影响很小, 而对电荷分布影响很大, 特别值得注意的是外电场引起了碳纳米管分子内的电荷转移, 这直接导致其β0极大地增加. 当F= 80 × 10-4au时, CNT(6, 3)的β0(F) 从23 au激增到34873 au, 外电场带来了一个非常大的β0(F)增大. 因此CNT(6, 3)可以成为以Fw= 80 × 10-4au为工作电场的非线性光学分子开关. 关于碳纳米管非线性光学开关的管径效应, 其中CNT(7, 3)的工作电场Fw为160 × 10-4au, 而CNT(3, 3)、CNT(4, 3)和CNT(5, 3)的工作电场Fw可选为200 × 10-4au. 需要特别关注的是, 本文提出的非线性光学开关是通过电场调控碳纳米管的电荷长程转移而实现的, 可称之为“电子结构异构化非线性光学开关”, 这种非线性光学开关具有灵敏、快速、可逆等优点. 此外, 电子吸收光谱表明这些碳纳米管具有小于300 nm和大于2500 nm的光学透明区, 因此它们可以作为紫外兼红外非线性光学开关的候选物.