基于三维离散元方法研究热点的位置和温度对奥克托今颗粒点火燃烧的影响

白志鑫， 甘云丹， 蒋城露， 赵 锋， 尚海林，李星翰， 刘福生，刘其军， 常相辉

(1. 西南交通大学 物理科学与技术学院， 成都 610031; 2. 西安近代化学研究所， 西安 710065;3. 中国工程物理研究院流体物理研究所， 绵阳 621900)

1 引 言

众所周知，炸药不仅在军事上为常规武器的毁伤以及核武器的内爆压缩提供爆轰能源，其也是国民经济建设(工程爆破、采矿等)中广泛应用的一种含能材料[1]. 然而，炸药在制作、贮存、运输、使用过程中可能会遭遇跌落、撞击、火烧等意外事故，这些意外事故也能在炸药内部形成各种形式的局部损伤. 在力、热刺激下，这些局部损伤能够形成热点，引发点火、燃烧、爆燃、爆轰等不同程度的反应，进而造成不可估量的灾难性后果[2, 3]. 研究表明，即使撞击和摩擦产生的温度远小于爆炸物的爆燃温度，爆炸物也有可能被点燃或引爆[4]. 因此，有关炸药安全性的研究就显得尤为重要. 众所周知，感度是衡量炸药安全性的重要指标之一，但在已经了解到某种炸药感度的情况下，为了保证其在应用过程中的安全性，对炸药的点火燃烧进行细致地研究具有非常重要的现实意义.

一般认为，非均相凝聚炸药在冲击波作用下的起爆关键是热点的形成[5]. 热点学说认为，炸药受到的机械作用是不均匀的，由机械能量转化为的热能不可能均匀作用在炸药上，而只是集中在炸药的局部位置，从而形成热点[6]. 针对热点的相关研究主要可以概括为两方面[7-13]：一方面是炸药在冲击波作用下热点的产生机制；另一方面是炸药热点的成长过程. 由于给予炸药初始条件不同(机械作用不同)，炸药颗粒产生的热点也不同，包括热点温度的不同以及热点相对于整个炸药颗粒位置的不同. 不同的热点对炸药颗粒的燃烧和起爆过程有至关重要的影响. 但是，在实际的研究中，很少有文献报道不同热点对炸药颗粒点火燃烧特性的影响. 因此，本文研究炸药的点火燃烧特性将热点的不同考虑在内是很有必要的.

随着计算机模拟技术的发展，由于其既可以提高实验的针对性，又可以减少不必要的实验，其在科学研究中发挥着越来越重要的作用. 热点的形成是炸药内部细观尺度结构相互作用的结果，因此细观数值模拟研究是探究炸药安全性的有效途径之一[1]. 离散元法最初主要应用于处理岩土工程和粉体工程等非连续介质的力学问题[14-17]. 近年来，它的应用领域又扩展到求解连续介质以及连续介质向非连续介质转化的力学问题[18]. 离散元法被应用于模拟炸药的冲击点火过程，起源于Tang等人建立的二维细观离散元模型，其可以用来模拟含有化学反应混合粉末的冲击合成过程[19, 20]. 由于二维离散元模型在应用方面的局限性，Tang等人又提出了三维离散元模型[21]. 近年来，三维离散元方法被广泛应用，成为研究炸药点火的有效手段之一.

因此，本文基于三维离散元方法，以HMX炸药颗粒为研究对象，探究不同的热点位置和初始温度对其燃烧特性的影响.

2 计算方法

离散元模型是假定整体材料可以离散成具有细观尺度的“元”，这些“元”具有质量、比热、相互作用等物理性质[19]. 离散元法的简单之处在于这些“元”之间的相互作用在任意时刻都满足经典牛顿运动方程[21, 22]:

(1)

中心势作用力模型由Hugoniot关系推导得出[2,12]:

(2)

塑性变形、摩擦力等都能引起能量的耗散，从而使离散元温度升高. 由于炸药颗粒的爆炸可以认为是一个瞬态过程，本文近似认为该过程是一个绝热过程，因此假定塑性变形与摩擦力的能量耗散全部转化为温度，即[2,12,20-24]:

(3)

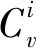
反应速率模型采用Arrhenius化学反应模型[2,12]:

(4)

其中，k为反应的速率常数，Ea为元的活化能，R为普适气体常量，T为热力学温度，λ表示反应度，取值为0≤λ≤1.

HMX爆炸膨胀采用JWL状态方程[2,12]:

(5)

其中，p是 HMX 爆炸产生的压力，V是元对应的体积，Qr为元中的能量.

本文的离散元模型为三维离散元模型，有关HMX离散元的物理参数设置见表1.

表1 HMX的计算参数

3 离散元模型

基于三维离散元方法，先后建立了能够反映炸药细观构型的以HMX为主体的单个颗粒离散元模型，如图1所示. 单个HMX炸药颗粒含有1629个离散元，每个离散元半径为10 um，其中蓝色离散元代表HMX炸药，7个红色离散元代表炸药中的热点，HMX离散元的初始温度为300 K(蓝色离散元). 本文通过给定红色离散元不同的初始温度和位置从而模拟不同的热点对HMX燃烧特性的影响.

本文一共建立了18个离散元模型，分别为热点在HMX炸药颗粒中心处(图1a)、边缘处(图1b)以及分散分布(图1c)，并且给不同的热点设定了不同的初始温度(400 K、500 K、600 K、700 K、800 K和900 K).

图1 HMX颗粒离散元模型:(a)热点位于炸药颗粒中心位置,(b)热点位于炸药颗粒边缘位置,(c)热点分散分布于炸药颗粒内部Fig. 1 HMX particle discrete element model: (a) hot spots are located in the center of explosive particles, (b) hot spots are located at the edge of explosive particles, (c) hot spots are dispersed in the interior of explosive particles

4 计算结果与分析

4.1 热点在HMX炸药颗粒中心位置时的燃烧过程

针对图1(a)的离散元模型，分别给定红色离散元的初始温度为400 K、500 K、600 K、700 K、800 K以及900 K，建立了6个离散元模型. 图2为具有400 K初始温度时，HMX炸药颗粒的燃烧过程，其中每个时刻HMX炸药颗粒三维图下方的三个小图分别是该时刻下炸药颗粒在X-Y平面、X-Z平面和Y-Z平面(从左到右)的图像. 从图中可以看出，在t=1.00μs时，炸药颗粒下方的温度首先升高，这是因为较高的红色离散元温度使得离散元体积发生膨胀，进而使得HMX炸药颗粒底部受到较大的挤压，底部离散元温度升高，出现了新的热点；在t=2.00μs时，红色离散元周围的离散元开始升温，这是热传导的结果；最后整个HMX炸药颗粒在热点的共同作用下燃烧.

4.2 热点在HMX炸药颗粒边缘位置时的燃烧过程

将图1(b)离散元模型红色部分的初始温度分别设置为400 K、500 K、600 K、700 K、800 K以及900 K，建立了6个离散元模型. 图3为热点在炸药颗粒边缘位置且初始温度为400 K时，HMX炸药颗粒的燃烧过程. 从图中可以发现，在t=1.00μs时，由于热传导作用，与红色离散元相邻的炸药颗粒离散元的温度有较小的升温. 与此同时，炸药颗粒底部的离散元的温度升高更明显，形成了新的热点. 这是因为此时的热传导速率较低，从而导致底部的离散元受到挤压先出现新的热点. 随着时间的推移，红色离散元的温度持续升高，使得其周围的离散元升温明显比底部的离散元升温快.

4.3 热点在HMX炸药颗粒内分散分布时的燃烧过程

将图1(c)离散元模型的热点初始温度分别设置为400 K、500 K、600 K、700 K、800 K以及900 K，建立了6个离散元模型. 结果发现，热点初始温度为400 K、500 K和600 K的炸药颗粒的燃烧过程相似，热点初始温度为700 K、800 K和900 K时炸药颗粒的燃烧过程相似. 因此，分别绘制了图4和图5. 图4为热点初始温度为400 K时HMX炸药颗粒的燃烧过程. 可以发现，在t=0.1272 μs时，与红色离散元(热点)相邻的离散元由于热传导作用开始升温；在t=0.1276 μs时，热点周围的离散元已经升温很明显. 随着时间的推移，整个炸药颗粒离散元温度全部升高. 图5为初始温度为700 K时HMX炸药颗粒的燃烧过程. 从图中可以看出，在t=0.5 μs时，HMX炸药颗粒的底部温度有所升高；随着时间的推移，红色离散元周围的离散元开始升温，在t=4.00 μs时能够很明显地观察到这一现象；随后在初始热点(红色离散元)以及新产生热点的作用下，整个HMX炸药颗粒温度明显升高.

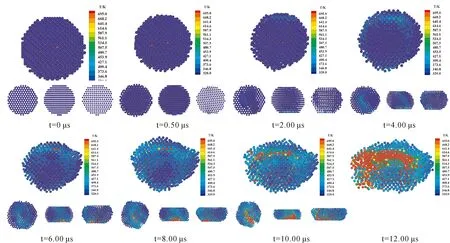
图5 热点分散于HMX炸药颗粒内部，其初始温度为700 K时的燃烧过程Fig. 5 The combustion process when hot spots are dispersed in HMX explosive particles and their initial temperature is 700 K

4.4 不同热点作用下HMX炸药的表观压强

众所周知，压强的急剧升高是炸药爆炸的主要特征之一[25]. 图6-图9分别为热点在炸药颗粒中心位置、边缘位置和分散分布时，HMX炸药颗粒的表观压强随时间的变化. 从图8可以看出，热点初始温度为400 K、500 K以及600 K时，HMX炸药颗粒的表观压强随时间有急剧的升高，其爆炸现象非常明显. 热点的初始温度能否引发自维持的化学反应主要取决于热点尺寸是否大或者热点初始温度是否高[5]. 分散分布的热点表面积较大，因此HMX炸药颗粒爆炸明显. 然而，从图9可以发现，热点在炸药颗粒内分散分布但其初始温度大于600 K以后，反而无法从压强变化图中观察到明显的爆炸现象. 这可能是因为温度太高，模型太小，使得HMX炸药颗粒在达到爆炸压力之前就燃烧完了. 同样地，从图6和图7也发现，无法从压强变化图中观察到明显的爆炸，这是因为中心或边缘位置的热点相比分散分布热点的表面积小，而设置的温度也没有达到自维持化学反应的条件.

图6 不同初始温度(位于炸药颗粒中心位置)的热点下HMX炸药表观压强随时间的变化Fig. 6 The apparent pressure changes with time of HMX explosive at hot spots with different initial temperatures (located at the center of explosive particles)

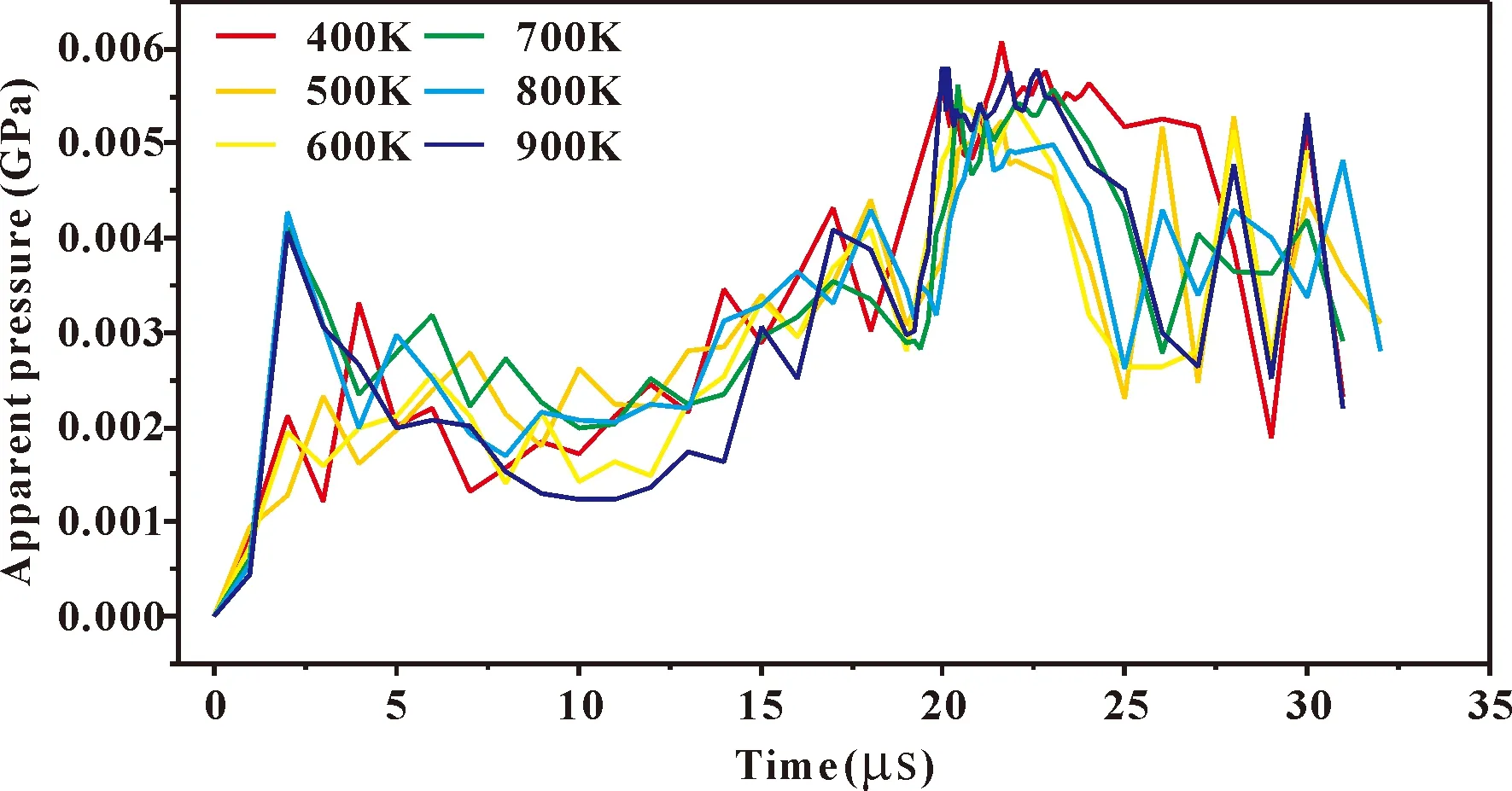
图7 不同初始温度(位于炸药颗粒边缘位置)的热点下HMX炸药表观压强随时间的变化Fig. 7 The apparent pressure changes with time of HMX explosive at hot spots with different initial temperatures (at the edge of explosive particles)

图8 400 K、500 K以及600 K的初始温度(分散分布)的热点下HMX炸药表观压强随时间的变化Fig. 8 The apparent pressure changes with time of HMX explosive at 400 K, 500 K and 600 K initial temperature (distributed) hot spots

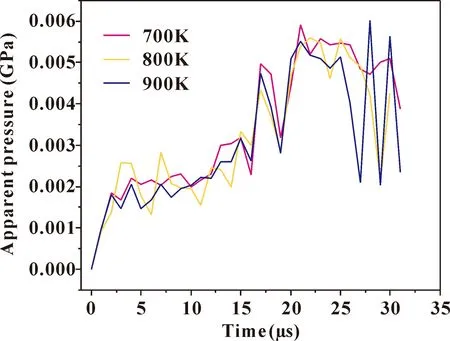
图9 700 K、800 K以及900 K的初始温度(分散分布)的热点下HMX炸药表观压强随时间的变化Fig. 9 The apparent pressure of HMX explosive varies with time at the hot spots of 700 K, 800 K and 900 K initial temperatures (distributed)

5 结 论

基于三维离散元方法，模拟得到了在不同热点作用下HMX炸药颗粒的燃烧过程，具体结论如下：

(1)同一HMX炸药颗粒，在不同热点作用下的燃烧特性是不同的，热点的初始温度和位置都会影响其燃烧特性；

(2)由于热点分散分布时的表面积要比热点集中分布时的表面积大，因此，在同一初始温度作用下，多个热点更有利于炸药的起爆；

(3)一般情况下，炸药起爆的关键在于热点的形成，但热点形成以后炸药也不一定有明显的爆炸现象，关键要看炸药中产生热点的尺寸和初始温度是否能够满足引发炸药爆炸的条件.