克尔介质中皮秒亮孤子多光子J-C模型粒子数反转特性
2022-05-12刘王云孙小斌张玉虹
刘王云, 孙小斌, 张玉虹
(1. 西安工业大学 光电工程学院, 西安 710021; 2. 安康市科技资源统筹中心, 安康 725000 )
1 引 言
光孤子由于在光纤中传输模式稳定,具有高码率、长距离和大容量、自动抗退相干能力强等特性而被广泛应用于光纤通讯领域. 随着研究手段的不断更新与发展,人们对光孤子的研究工作不仅从理论走向实验、进而深入到通信工程的应用阶段[1-6],而且还从经典光孤子深入到量子光孤子领域,对量子光孤子的基本性质及光孤子的量子态对光纤通信的影响都有研究[7-14]. 通过研究克尔介质中的光孤子[15,16],得到大部分的光传输基于基态孤子,基态孤子能稳定地存在局域克尔型非线性介质中[17],基孤子本质上遵循单模动力学[18]. 近年来人们也将Jaynes-Cummings模型与处于克尔介质中的腔场相结合,研究克尔介质对原子的动力学特性及光场特性的影响[19-22].
因为光孤子和克尔介质在量子光通讯领域有着重要作用,然而目前尚未见到有关克尔介质中皮秒光孤子与二能级原子多光子相互作用过程中粒子数反转变化情况的研究,所以本文采用全量子理论研究皮秒孤子场与理想二能级原子相互作用系统中粒子数反转随时间的变化特性. 借助编程分析软件讨论了各参数的变化对于粒子数反转的影响,并得到了一些新的结果,期望对量子光通讯领域中信息的传输与存储提供一点参考.
2 理论模型及其解
根据文献[12]所定义的皮秒亮基孤子光场的光子湮灭和产生算符
其中
(1)
(2)
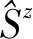
设初始时刻,原子为激发态,光场为皮秒亮基孤子态,即
|ψa(0)〉=|e〉
(3)
(4)
并且此时场与原子间不存在任何相互作用,即系统态矢量可以表示为
|ψ(0)〉=|ψa(0)〉⊗|ψf(0)〉=
(5)
任意时刻系统的态矢量变为
B(t)|g,n+K,p,t〉H]
(6)
该态矢量应满足下列方程
(7)
将(2)、(6)式代入(7)式得微分方程组
(8)
由A(0)=1,B(0)=0,可知方程组的解为
(9)
(10)
为原子Rabi振荡频率.
由(6)、(9)、(10)式可得粒子数反转为
(11)
3 数值计算结果与讨论
由式(11)给出的粒子数反转表达式中的级数很难精确求解,所以借助MATLAB软件对其作数值计算,形象直观地展现出粒子数反转随时间演化的动力学特性.
3.1 初始平均光子数对粒子数反转的影响
图1所示为χ=0初始平均光子数分别是10、15、20、30时所得到的粒子数反转情况. 由图可知,随着时间的推移,粒子数反转呈现周期性的崩塌与恢复现象,且恢复时间是nπ(n=1,2,3,…),该周期不随初始平均光子数的改变而发生变化,初始平均光子数越多,崩塌恢复振荡的幅值越小.
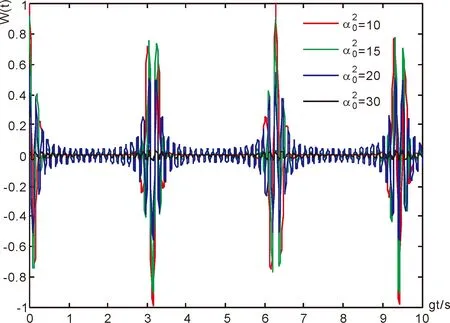
图1 不同初始平均光子数时粒子数反转随时间的演化曲线Fig. 1 The evolution curves of atomic inversion over time for different initial mean photon numbers
3.2 克尔介质与场模非线性相互作用强弱对粒子数反转的影响
图2所示为K=2克尔介质与场模非线性作用的强弱分别是χ=0.2g、g、3g、5g时所得到的粒子数反转情况. 由图可知,随着非线性相互作用的增强,粒子数反转崩塌与恢复的周期及振荡幅度不断减小,演化曲线的平均值增大.
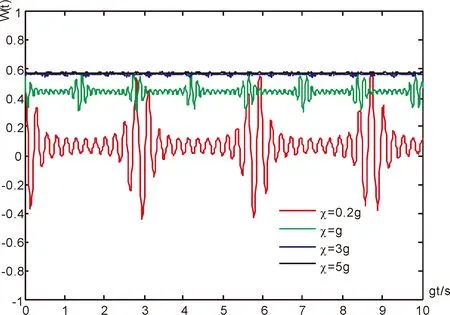
图2 克尔介质与场模非线性相互作用不同时粒子数反转随时间的演化曲线Fig. 2 The evolution curves of atomic inversion over time when the nonlinear interaction between Kerr medium and field mode is different
3.3 孤子光场与原子间相互作用耦合强度对粒子数反转的影响
图3所示为|α0|2=10,K=4,χ=1,耦合强度g=0.2、0.5、1、2时所得到的粒子数反转情况. 由图可知,随着孤子光场与原子间相互作用耦合强度的增大,粒子数反转崩塌与恢复的周期及平均值不断减小,且崩塌恢复的振荡幅度逐渐增大.
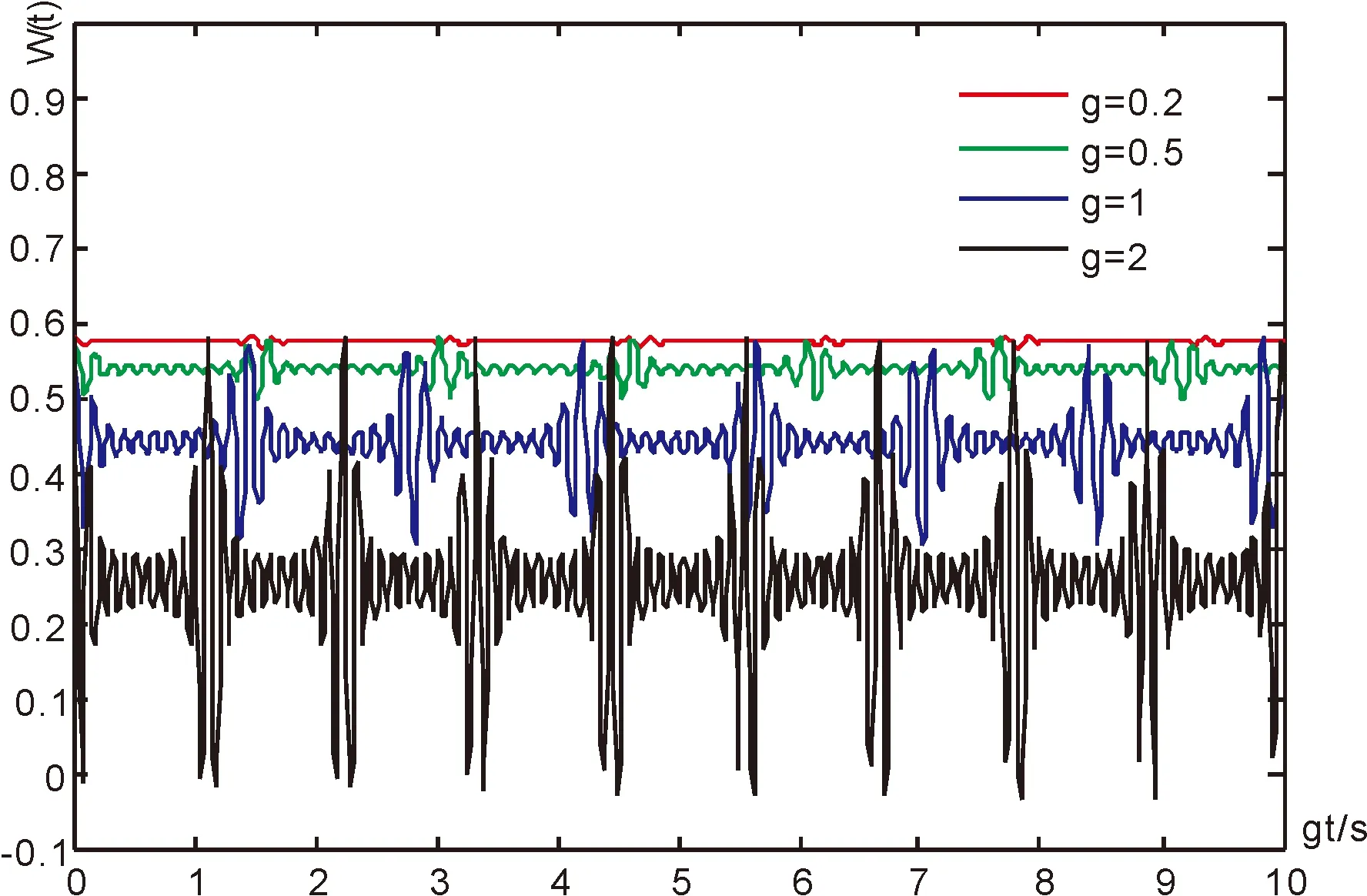
图3 孤子光场与原子间相互作用耦合强度不同时粒子数反转随时间的演化曲线Fig. 3 The evolution curves of atomic inversion over time with different coupling strengths of soliton light field and atomic interaction
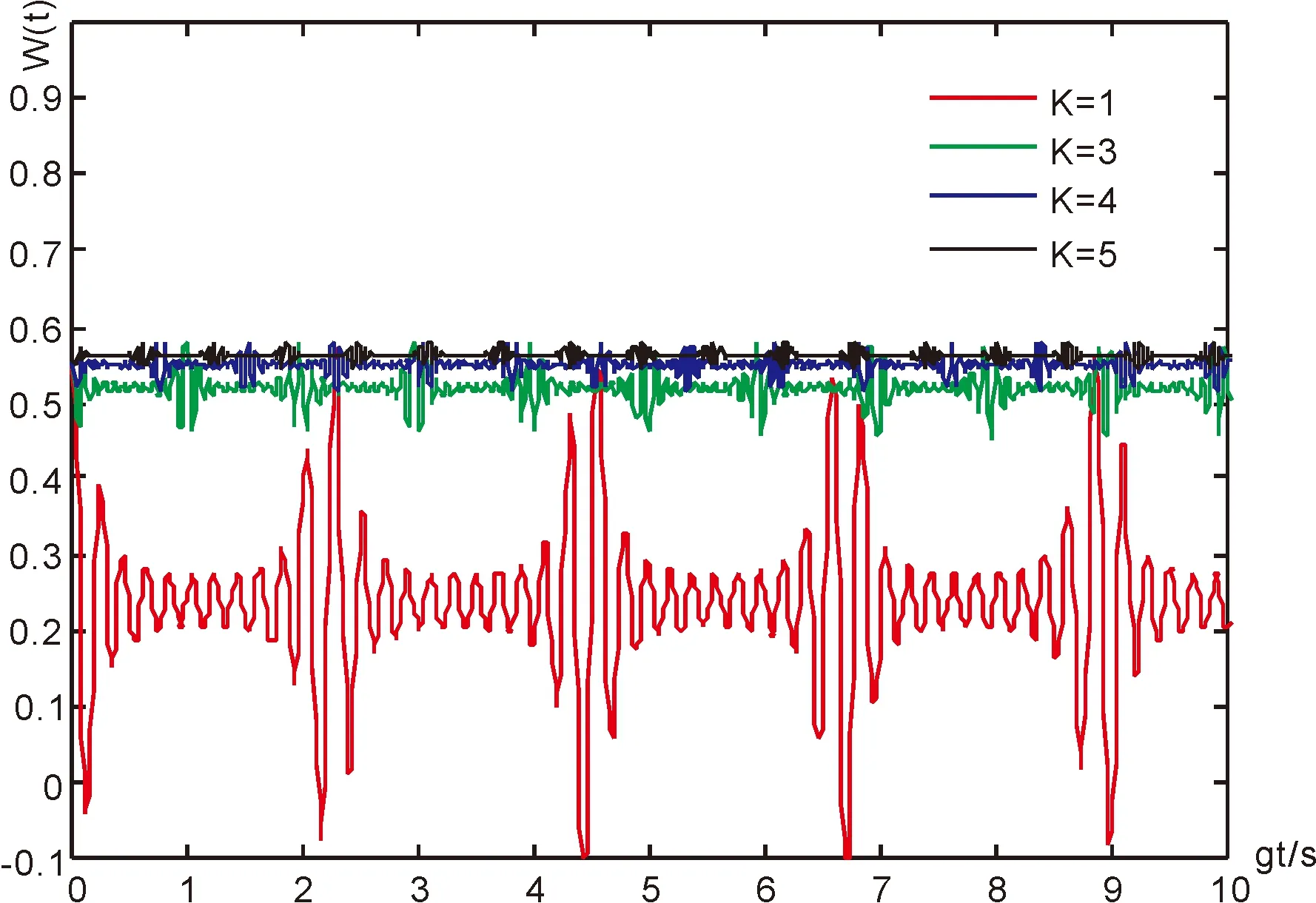
图4 相互作用过程中光子简并度不同时粒子数反转随时间的演化曲线Fig. 4 The evolution curves of atomic inversion over time with different photon degeneracies during interaction
3.4 相互作用过程中光子简并度对粒子数反转的影响
图4所示为|α0|2=10,K=4,χ=1,相互作用过程中光子简并度分别为K=1、3、4、5时所得到的粒子数反转情况. 由图可知,随着相互作用过程中光子简并度的增大,粒子数反转崩塌与恢复的周期及振荡幅度不断减小,且崩塌恢复的平均值不断增大.
4 结 论
本文通过对克尔介质中皮秒亮孤子光场与一个二能级原子多光子共振相互作用系统的研究,获得了粒子数反转的演化表达式,并用MATLAB软件编程模拟了初始平均光子数、克尔介质与场模非线性相互作用强弱、孤子光场与原子间相互作用耦合强度以及相互作用过程中光子简并度对粒子数反转的影响,并得到如下结果:
(1).初始平均光子数越大,粒子数反转的崩塌与恢复振荡的幅度越小,周期不变;
(2).随着克尔介质与场模非线性相互作用的增强,粒子数反转崩塌与恢复的周期及振荡幅度不断减小、平均值增大;
(3).随着孤子场与原子之间相互作用耦合强度的增大,粒子数反转崩塌与恢复的周期及平均值不断减小、振荡幅度逐渐增大;
(4).随着相互作用过程中光子简并度的增大,粒子数反转的崩塌与恢复周期及振荡幅度不断减小、平均值不断增大.
