高压电抗器绕组和铁芯机械故障的混沌特性分析与特征识别

2022-05-11马宏忠侯鹏飞吴金利

电力自动化设备 2022年5期

马宏忠，侯鹏飞，严岩，吴金利，陈轩，朱超

（1. 河海大学能源与电气学院，江苏南京 211100；2. 国网江苏省电力有限公司检修分公司，江苏南京 211102）

0 引言

高压并联电抗器（下文简称高抗）作为电网中的重要电力设备，主要用于补偿无功和稳定电压，其安全性和稳定性对电网的安全稳定运行具有重要意义［1］。在机械力或电磁力的作用下，高抗绕组和铁芯的结构易发生变化，如绕组松动、绕组变形、绕组鼓包、铁芯松动、硅钢片间磨损等［2-3］，对高抗的安全稳定运行造成极大隐患，并且这些内部构件的机械变化无法通过常规的油色谱和局部放电等诊断方法进行检测。因此，有必要针对高抗绕组和铁芯的机械状态检测技术进行深入研究，及时掌握和发现高抗内部机械状态的变化，这对保障高抗的安全稳定运行至关重要。

基于振动信号的检测方法对电抗器内部机械结构的改变具有极好的灵敏性，近年来得到了越来越多的关注。运行状态下，高抗的振动信号呈现出显著的非线性特性，蕴含了重要且全面的状态信息。高抗箱体的振动信号能够有效体现高抗绕组和铁芯的机械状态的变化［4］。但是，在高抗绕组和铁芯发生潜伏性机械故障的早期阶段，受变电站现场环境的影响，能够反映高抗内部机械状态变化的微弱故障特征易被强大的背景噪声覆盖，且当高抗内部发生多处机械故障或混合故障时，可能存在故障特征耦合或削弱的情况，所以从高抗的振动信号中准确有效地提取故障特征量是诊断高抗绕组和铁芯机械故障的关键。

目前，振动信号特征的提取方法有时域分析法、经验小波变换、小波分析、希尔伯特-黄变换、经验模态分解等［5-7］，这些方法大多基于线性理论，在处理非线性信号时易出现端点效应、能量泄漏、模态混叠等问题，严重影响特征提取的准确性。因此，对于非线性振动信号，上述线性分析方法不能充分、准确地捕捉振动信号的特征。相对而言，非线性时域分析方法，如分形技术、混沌理论和相空间重构技术等，能够很好地描述非线性振动信号的本质特征和内在规律。目前，相空间重构技术已应用于火箭发动机、航空电弧识别、光伏发电及电力负荷预测等多个领域［8-10］，但在振动信号分析的相关领域应用有限。文献［11］利用核可能性聚类分析相轨迹特征量，识别了变压器绕组松动故障，不足之处在于核可能性聚类分析对相轨迹特征量的识别能力有限，聚类数目的选取直接影响分类识别的效果。文献［12］通过振动信号的相平面轨线定性分析和形态变化识别变压器绕组松动故障，但其对嵌入维数的取值缺少理论依据，可能诱发误判，且其忽略了多维相空间的其他关键特征，缺乏定量计算识别。文献［13］将相轨迹的分布系数作为故障特征对振动信号进行分析，但忽略了相轨迹的其他重要信息，特征量提取能力有限。

鉴于上述问题，本文从高抗振动信号的混沌动力学特性着手，首先通过Kolmogorov 熵（下文简称K熵）值证明高抗振动信号的混沌特性，进而计算延迟时间和嵌入维数，在此基础上重构高抗绕组和铁芯在不同机械故障下的振动信号，研究不同机械故障下高抗振动信号相轨迹的变化规律；然后计算用于表征振动信号相轨迹恒定测度与遍历量的多混沌指标，即关联维数、最大Lyapunov 指数、K 熵值，提出具有工程应用价值的多混沌特征空间识别法，以期为现场高抗绕组和铁芯机械故障特征的提取和识别提供理论依据。

1 高抗振动信号的相空间重构

为了充分揭示高抗振动信号所包含的状态信息，本文利用相空间重构对其进行分析。相空间重构能够将振动信号的1 维时间序列扩展至3 维或更高维的空间中，从其时间序列中提取和恢复出高抗动力系统的所有状态信息和规律［8］，具体原理如下。

设采集到的高抗振动信号时间序列为：

式中：m为嵌入维数；τ为延迟时间。

由于τ和m的值直接影响相轨迹的空间分布，因此在重构振动信号时必须慎重选取τ和m。根据Takens定理［14］可知，在无限长、零噪声的理想时间序列中，τ和m可随意取值，但实际测得的高抗振动信号时间序列长度为一定值，且通常存在环境噪声干扰，所以为了保证相轨迹的质量，本文对τ和m的取值进行准确计算。

1.1 延迟时间τ的选取

延迟时间τ的取值决定了振动信号不同分量之间的相关性，因此必须合理地选取τ值。如果τ值过大，则会导致电抗器动力系统中各时刻的状态相关性减弱或变得不相关，相邻轨迹出现分叉，从而导致高抗状态信息的严重缺失；如果τ值过小，则会导致坐标关联性过强，相轨迹易出现收缩变形的现象，无法完全呈现振动信号蕴含的信息。目前，用于确定τ的方法有自相关函数法、填充因子法、平均位移法和互信息法等。考虑到互信息法所提取的时间序列既有非线性特征也有线性特征，其计算结果的准确性更高，所以本文选用互信息法求解高抗振动信号的最佳延迟时间。

将高抗振动信号时间序列x={x(i)，i=1，2，…，N}经延迟时间τ后改写为xτ={x(i+τ)，i=1，2，…，N}，根据Shannon 信息熵和概率分布［15］得到x和xτ的互信息I(τ)为：

式中：H(x)和H(xτ)分别为x和xτ的信息熵；H(x，xτ)为x和xτ的联合信息熵；P(x(i))和P(x(i+τ))分别为x(i)和x(i+τ)的发生概率；P(x(i)，x(j+τ))为x(i)和x(j+τ)的联合发生概率。由式（3）绘制延迟时间与互信息值的变化曲线，根据互信息法准则，本文选取互信息值曲线上第1 个极小值对应的时间为最佳延迟时间τopt。额定电压下，处于正常状态（状态1）、高抗绕组和铁芯轴向完全松动状态（状态2）、高抗绕组和铁芯径向完全松动状态（状态3）的高抗的侧面某测点的振动信号如图1 所示，图2 为对应的互信息值-延迟时间曲线。

图1 额定电压下，处于不同机械状态的高抗的振动信号Fig.1 Vibration signal of high-voltage shunt reactor with rated voltage in different mechanical states

图2 额定电压下，处于不同机械状态的高抗的振动信号的互信息值-延迟时间曲线Fig.2 I(τ)-τ curve of vibration signal of high-voltage shunt reactor with rated voltage in different mechanical states

1.2 嵌入维数m的选取

合理地选取嵌入维数有利于充分揭示高抗动力系统的动力学特性，当重构相空间的维数达到或超过嵌入维数时，重构信号可以完全打开，避免出现自交叉现象。目前，计算嵌入维数的方法有C-C 法、伪邻近点法、G-P 算法等。为了缩短运算时间，本文运用优化的G-P算法［16］计算m值，具体如下。

为降低计算量，本文利用式（4）所示的递推公式求解高抗振动信号重构空间内任何两点间的欧氏距离rij。

式中：r为相空间中两点间的距离；C(m，r)为第m维相轨迹关联积分函数，代表相空间中任意两点间距离小于r的概率。在r的一定范围内，关联维数D(m)与C(m，r)存在线性关系，满足D(m)=lnC(m，r)/lnr，增加m的取值，直到D(m)保持相对稳定且不发生显著变化，此时对应的m即为最佳嵌入维数mopt。对图1 中高抗在正常状态下的振动信号进行计算，相应的m取值范围为［1，9］，得到lnC(m，r)随lnr的变化曲线如图3所示。

图3 ln C（m，r）随ln r的变化曲线Fig.3 Change curve of ln C（m，r）vs. ln r

由图3 可知，当m=3 时，曲线的线性部分基本保持稳定且随着m的增加其不再发生变化，所以取mopt=3，对应的D（mopt）=1.0852。

2 高抗绕组和铁芯机械故障敏感特征的相轨迹混沌指标

为了更加准确地描述高抗动力系统混沌特性的变化，本文在定性分析高抗振动信号相轨迹几何特性的基础上，采用多混沌指标对高抗振动信号的混沌特征进行定量计算。关联维数作为分形维数的一种，可有效反映相轨迹的动态结构和不均匀度。最大Lyapunov指数是判断系统混沌程度的一个重要指标，体现了系统混沌特性的强弱。K 熵作为混沌特性的另一个度量指标，能够很好地描绘非线性系统的状态演化。本文利用关联维数、最大Lyapunov 指数和K 熵分别对高抗正常状态和机械故障状态下的振动信号相轨迹进行定量计算，分析故障前后高抗动力抗系统混沌特性的变化规律。

2.1 关联维数

相轨迹是轨迹在相空间中多次逼近、远离、折叠、延伸所构成的不规则图形，其形态特性可以通过分形维数进行研究。关联维数作为一种分形维数，对电抗器动力系统的时间序列非常敏感，能够准确有效地量化系统相轨迹性质。在1.2节中，关联维数D(m)的求解已介绍，其运算公式为：

2.2 最大Lyapunov指数

混沌运动对初值前提非常敏感，Lyapunov 指数是用于定量描绘2 个相近初值随着时间变化以指数形式分开生成轨迹的量。Lyapunov指数量化了附近轨迹的发散率。在一维动力系统中，Lyapunov 指数λ的求解表达式为［16］：

式中：n为时间序列长度。通常情况下，无须求解所有Lyapunov 指数，只需计算决定轨迹发散率的最大Lyapunov 指数λmax即可。用于求解最大Lyapunov指数的方法有定义法、小数据量法、Wolf法等。考虑计算结果的准确性，本文采用小数据量法计算最大Lyapunov指数，具体计算过程参见文献［17］，本文不再赘述。

2.3 K熵

K 熵作为判断系统混沌特性的重要指标之一，用于度量非线性系统运动状态的变化。相关积分法与最大似然估计法常被用于求解K 熵值。考虑到相关积分法运算速率高的特点，本文采用相关积分法求解K熵，K熵的计算表达式为［8］：

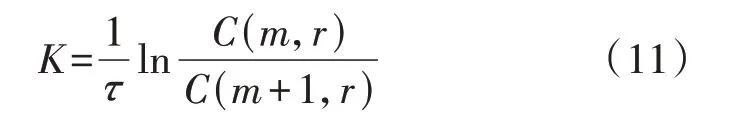
式中：C(m+1，r)为第m+1维关联积分函数。一般选择不再随着m的变化而变化的稳定K值作为K 熵的估计值。根据K 熵值的范围判断系统的无序程度：当K=0 时，系统做规则运动；当K→∞时，系统做随机运动；当K＞0且为常数时，系统做混沌运动［8］。

3 高抗振动信号实验采集

3.1 实验系统的搭建

本文以一台型号为JSRT-ACL11H 的10 kV 单相油浸式高抗为研究对象，进行故障模拟和振动信号采集。实验系统如附录A 图A1所示，该系统主要由交流电源、调压器、限流电阻、变压器、高抗、电容器、振动加速度传感器、DH5922D 振动信号采集仪等组成。振动信号采样频率设定为20 kHz，每组信号采样时间为5～10 s，对每种状态采集6—10 组数据。加速度传感器型号为1A212E，灵敏度为500 mV/g（g=9.8 m／s2）。加速度传感器在高抗箱体表面采用阵列的方式布局，高抗侧面设置3 行16 列共计48 个测点，顶面设置5 个测点，详细的测点布局如附录A图A2所示。

3.2 故障设置

为了研究不同电压等级、不同机械故障类型及故障程度下高抗振动信号相轨迹的变化特性，本文分别在85%UN、90%UN、…、105%UN（UN为额定电压）这5 种电压等级下，对高抗绕组和铁芯轴向松动以及高抗绕组和铁芯径向松动两大类机械故障进行模拟实验。其中，高抗绕组和铁芯轴向松动故障程度分别设置为轴向松动50%（轴向预紧力为50%的轴向标准预紧力）、轴向松动100%（轴向预紧力为0）；高抗绕组铁芯径向松动故障程度分别设置为径向松动30%（径向预紧力为70%的径向标准预紧力）、径向松动60%（径向预紧力为40%的径向标准预紧力）、径向松动100%（径向预紧力为0）。

高抗绕组和铁芯轴向和径向松动的具体位置如附录A 图A3所示。额定电压下，正常状态的高抗箱体侧面的振动强度分布情况如附录A 图A4 所示。考虑到高抗箱体表面振动强度越大的位置越有利于发现机械故障，本文采用高抗箱体侧面振动强度较高的18号测点进行分析，18号测点在不同机械状态下的振动信号如附录A图A5所示。

4 高抗振动信号相轨迹特征分析与识别

4.1 高抗振动信号混沌特性判断

在分析高抗振动信号相轨迹前，需要判断信号是否具备混沌特性，本文利用2.3节中度量系统无序程度的K 熵值对高抗振动信号的混沌特性进行判断。18号测点额定电压不同状态下的K熵计算结果如表1所示。由表可知，在不同机械状态下，18号测点的K 熵值均大于0 且为常数，证明高抗的振动信号具有混沌特性，可以采用相空间重构理论进行分析。

表1 K熵计算结果Table 1 Calculation results of Kolmogorov entropy

4.2 不同电压等级与不同机械故障类型下相轨迹的变化规律

考虑到实际应用问题，本文采用额定电压下不同机械状态对应的最佳延迟时间和最佳嵌入维数对图A5 所示的高抗振动信号进行相轨迹分析，其中，正常状态、高抗绕组和铁芯轴向松动50%以及高抗绕组和铁芯轴向松动100%状态下的最佳延迟时间分别为13、15 以及15，高抗绕组和铁芯径向松动30%、径向松动60%和径向松动100%状态下的最佳延迟时间分别为11、13和11，按照1.2节求解得到高抗在不同机械状态下的最佳嵌入维数均为3。进一步地，利用计算得到的τopt和mopt对18 号测点振动信号进行重构，深入分析不同电压等级和不同状态下相轨迹形态变化规律。

1）电压等级和机械故障类型对高抗振动信号相轨迹的影响。

分别在电压等级为85%UN、90%UN、…、105%UN时，分析正常、高抗绕组和铁芯轴向松动100%以及高抗绕组和铁芯径向松动100%这3 种机械状态下18号测点的振动信号相轨迹，结果如附录A图A6所示。由图可见，不同机械状态和电压等级下，振动信号相轨迹均呈不规则的闭合环状。对比同一机械状态、不同电压等级下的振动信号相轨迹可知，随着电压等级的升高，相轨迹会发生不同程度的变化，不规则环状相轨迹环绕的体积逐渐增大，特别是当电压等级超过额定电压后，不规则环状相轨迹环绕的体积明显增加，其形态结构也发生了显著变化。需要说明的是，当电压等级低于额定电压时，同一机械状态、不同电压等级下的振动信号相轨迹形态结构具有一定的相似性。然而，同一电压等级、不同机械状态下的振动信号相轨迹的形态结构明显不同，存在较大差异。

通过上述分析可知，高抗电压等级的变化、高抗绕组和铁芯机械状态的改变均会影响高抗系统的动力学特性。高抗振动信号相轨迹的路径和形态能够有效反映不同电压等级下高抗绕组和铁芯的机械状态变化。由高抗绕组和铁芯的机械状态变化和电压等级变化造成的动力学特性变化程度不同，所导致的相轨迹形态特征变化也不同。不难发现，在本文中由高抗绕组和铁芯机械状态变化导致的相轨迹路径和形态改变程度比电压等级改变所导致的变化程度更加明显。

2）额定电压下，机械故障类型和故障程度对高抗振动信号相轨迹的影响。

早期阶段的高抗绕组和铁芯松动故障的故障特征微弱，易被现场环境噪声掩盖而难以提取，因此本文对不同故障程度下，高抗振动信号相轨迹的形态特征进行分析，探究轻微机械故障下相轨迹的变化规律，提取相轨迹特征量。电压等级为额定电压时，正常状态以及不同程度的高抗绕组和铁芯轴向和径向松动故障下，18 号测点的振动信号相轨迹如图4所示。

图4 正常状态和不同故障程度下，18号测点的振动信号相轨迹Fig.4 Phase trajectory of vibration signal at Measuring Point No.18 under normal state and different fault levels

分析图4 可知：发生高抗绕组和铁芯轴向松动故障后，振动信号相轨迹出现偏离正常状态下相轨迹的现象，其不规则环状结构整体呈现横向拉伸趋势，底部出现轻微缠绕，顶端呈扁平发展趋势，随着轴向松动故障程度的增加，相轨迹底部进一步缠绕，顶部呈现扁平状；发生高抗绕组和铁芯径向松动故障后，不规则环状相轨迹所环绕的体积增大且相轨迹中下部的凹陷程度增加；随着径向松动故障程度的增加，相轨迹所环绕的体积和其中下部凹陷程度均呈递增趋势，当径向完全松动时凹陷部的相轨迹与对侧轨迹出现轻微交叉折叠现象。

虽然不同故障程度下的高抗振动信号的相轨迹存在规律性变化，然而在现场应用时难以进行准确判断和描述，因此，本文利用多混沌指标，即最大Lyapunov 指数、K 熵、关联维数对高抗振动信号相轨迹的变化进行量化计算和阈值划分。

4.3 基于多混沌指标的高抗绕组和铁芯机械故障特征识别

为了准确描述和识别高抗振动信号相轨迹的变化程度，本文最大Lyapunov指数、K熵、关联维数这3个混沌指标定量计算和识别相轨迹的形态特征。在电压等级为额定电压时，从各种机械状态下的18 号测点振动信号中随机选取20 组数据（每组数据时长为0.2 s）计算混沌指标，结果如图5所示。

图5 最大Lyapunov指数、K熵、关联维数的计算结果Fig.5 Calculation results of maximum Lyapunov exponent，Kolmogorov entropy and correlation dimension

由图5 可见，高抗绕组和铁芯机械状态的改变会导致相轨迹的最大Lyapunov 指数、K 熵、关联维数发生改变，具体分析如下。

1）由图5中最大Lyapunov指数λmax的曲线可见：正常状态下，最大Lyapunov 指数在［0.006 9，0.011 0］范围内变化；高抗绕组和铁芯轴向松动50%、100%与径向松动30%、60%、100%故障下，最大Lyapunov指数的波动范围分别为［0.003 3，0.007 9］、［0.000 3，0.002 0］与［0.001 3，0.002 9］、［0.001 6，0.003 9］、［0.000 7，0.002 2］。由此可知，最大Lyapunov 指数可以有效识别高抗内部构件的机械状态变化，且在同一机械状态下最大Lyapunov 指数能够保持相对稳定。虽然最大Lyapunov指数在故障程度识别方面能力有限，但其可作为识别机械故障类型的敏感特征指标之一。

2）由图5 中K 熵值K的曲线可知：K 熵值随着高抗绕组和铁芯松动故障程度的增加而增加；正常状态下K 熵值的波动范围为［0.93，3.90］，高抗绕组和铁芯轴向松动50%、100%故障下K熵值的波动范围分别为［12.31，15.42］、［18.37，20.53］，高抗绕组和铁芯径向松动30%、60%、100%故障下，K熵值的波动范围分别为［10.29，14.89］、［23.18，26.04］、［28.46，29.02］。由此可知，额定电压下，不同机械故障类型和同一机械故障类型、不同故障程度下的K 熵值均具有良好的分离性和一致性。因此K 熵可用于识别不同故障程度，能够作为高抗绕组铁芯机械故障类型和故障程度的敏感特征。

3）通过图5 中关联维数D(m)的曲线可知：正常状态下K 熵值的波动范围为［1.082，1.084］，高抗绕组和铁芯轴向松动50%、100%故障下K 熵值的波动范围分别为［1.065，1.070］、［1.138，1.143］，高抗绕组和铁芯径向松动30%、60%、100%故障下，K熵值的波动范围分别为［1.184，1.195］、［1.069，1.072］、［1.110，1.120］。可以看出，同一机械故障类型、不同故障程度下的关联维数波动范围存在一定差异，利用关联维数能够识别不同故障程度，故关联维数也可以作为高抗绕组铁芯机械故障检测和分类的另一新敏感特征指标。

综上可知，通过最大Lyapunov 指数、K 熵、关联维数能够有效识别正常状态和机械故障状态，并且可对同一机械故障类型的不同故障程度进行区分。但是单一的混沌指标对高抗机械状态的识别准确性有待验证。为了更加准确地识别高抗绕组和铁芯的机械状态变化，本文利用最大Lyapunov 指数、K 熵、关联维数构成混沌特征空间对高抗的机械状态进行识别，混沌特征空间如图6所示。

图6 混沌特征空间的高抗机械状态识别结果Fig.6 Mechanical state identification results of highvoltage shunt reactor by chaotic feature space

由图6 可见，在混沌特征空间中，高抗绕组和铁芯轴向松动和径向松动故障被有效地分开，不同的松动程度也得到了清晰的显示，且不同机械状态的集群均未出现混叠交叉的现象。因此，本文构造的混沌特征空间可精确、有效地识别不同的高抗绕组和铁芯机械故障及故障程度。值得说明的是，该混沌特征空间不需要大量的训练样本和深度学习即可准确完成高抗绕组和铁芯机械故障分类识别，有助于解决当前智能学习算法存在的现场故障样本不足的问题。

在实际应用中，需要考虑正常状态下3 个混沌指标的阈值范围。图6 中，高抗正常状态下的最大Lyapunov 指数、K 熵、关联维数的阈值范围分别为［0.007，0.011］、［0.926，3.895］和［1.082，1.084］，3 个混沌指标同时满足上述阈值范围时才可识别为正常状态，如果有一指标值不在相应的范围内则识别为机械故障状态。进一步地，若混沌指标在已知机械故障的簇集阈值范围内，则识别为已知故障，反之，则识别为未知的新故障。

4.4 对比验证

为了验证本文方法的优越性，选取支持向量机（SVM）［18］、K 最近邻（KNN）［19］、决策树（DT）［20］法与本文方法进行对比。利用SVM、KNN 和DT 法分别对本文所研究的各种机械状态下的高抗振动信号的时、频域特征进行识别，其中，时域特征采用振动信号的最大值和最小值，频域特征采用100 Hz 及其倍频（1 000 Hz 以内）的幅值。随机选取高抗箱体表面的53 个测点在6 种机械状态下共计3 180 组数据进行时域和频域特征提取，其中70%的数据用于训练，30%的数据用于测试，计算得到120×53 维的时域特征矩阵和3 180×10 维的频域特征矩阵。不同方法的总体故障识别准确率ra如表2所示，不同方法对不同程度的高抗绕组和铁芯轴向松动、径向松动故障的总体识别准确率分别如附录A 表A1 和A2所示。

表2 不同方法的总体故障识别准确率Table 2 Overall fault identification accuracy of different methods

由表2 可知，与利用频域和时域特征的SVM、KNN、DT 方法相比，本文方法的总体故障识别准确率分别提高了13.8%、13.3%、14.6%和8.83%、13.9%、19.4%。进一步地，由表A1、A2 可知，对不同程度的高抗绕组和铁芯轴向松动、径向松动故障进行识别时，本文方法的总体识别准确率比SVM、KNN、DT方法至少高5%。由此可知，与SVM、KNN、DT 方法相比，本文方法具有一定的故障识别优势。同时，本文方法不需要监督学习和大量数据训练，对微弱故障特征敏感，有利于现场的实际应用。