基于SE-DSCNN的MMC开关管故障诊断方法

2022-05-11曾昭瑢何怡刚

电力自动化设备 2022年5期

曾昭瑢，何怡刚

（武汉大学电气与自动化学院，湖北武汉 430072）

0 引言

模块化多电平变换器MMC（Modular Multilevel Converter）作为变换器中最具吸引力的拓扑结构之一，凭借着模块化、易扩展、设计灵活、效率高及谐波性能好等优点，被应用于中压电机驱动、高压直流输电系统、统一潮流控制器等场景中［1-3］。MMC由多个级联子模块SM（Sub-Module）组成，每个SM 中又包含多个功率半导体器件。一旦发生故障，会产生三相不对称、过电流及电压电流波形畸变等不良影响［4］。因此，对故障部位进行快速、准确的诊断具有重要的实际意义。

MMC 中的开关管可能会发生开路或短路故障，通常短路故障在硬件保护装置执行隔离操作后会转化为开路故障［5］，因此MMC 故障诊断研究主要是针对其开关管的开路故障。多电平变换器的开路故障诊断方法包括基于模型、基于机器学习的方法等。基于模型的方法需要建立系统的数学或物理模型，通过比较测量的输出值和模型的估计值来进行故障诊断。文献［6］借助观测器来检测和定位开关管的开路故障，文献［7］建立SM 分组输出电压的预测模型以判断故障类型，这类方法需要设置故障阈值。如果阈值设置过小，则可能会造成故障误判；如果阈值设置过大，则很难在特征不明显的故障早期实现诊断。此外，该类方法还易受到系统参数变化的影响，具有一定的局限性。传统机器学习的故障诊断方法通常分为人工特征提取、故障分类两步。文献［8］先用主成分分析PCA（Principal Component Analysis）选取输出电压经快速傅里叶变换FFT（Fast Fourier Transform）后的特征，再利用多分类相关向量机mRVM（multiclass Relevance Vector Machine）进行故障分类。文献［9］使用小波包分解WPD（Wavelet Packet Decomposition）和PCA提取电容电压的故障特征，基于遗传算法GA（Genetic Algorithm）优化后的BP 神经网络区分故障的开关管。这类方法中的人工特征提取通常依赖大量的先验知识，需要根据分类结果不断调整所选特征，很难获得数据中的深层特征。而深度学习可以解决这个问题，其将特征提取和故障分类合并成一个模型，模型自动从数据中学习特征信息的表示方法，在实现自动提取特征信息的同时提高模型的分类性能。文献［10］使用深度学习中的栈式稀疏自动编码器SSAE（Stacked Sparse Auto-Encoder）和Softmax 分类器对故障子模块进行定位，但未考虑对故障开关管的定位。

为了快速、准确地定位MMC 故障开关管，识别特征不够明显的早期故障，本文基于深度学习，将故障诊断问题转变成分类问题，采用一种结合挤压-激励SE（Squeeze-and-Excitation）模块的深度可分离卷积神经网络DSCNN（Depthwise Separable Convolu-tional Neural Network）（简记为SE-DSCNN），自动提取深层故障特征，在网络结构参数缩减的情况下仍有较好的诊断效果。

1 MMC的运行原理及故障分析

1.1 MMC的拓扑结构及工作原理

MMC 逆变器的拓扑结构如图1 所示，每相包括上、下2个桥臂，各桥臂分别由N个结构相同的SM和一个桥臂电感L0串联而成，上、下桥臂的中点作为交流出口连接到负载，每个SM 由2 个带反并联二极管的IGBT（S1、S2）和一个电容C构成。图中：Udc为直流侧电压；uSM为SM输出电压；uC为电容两端电压。

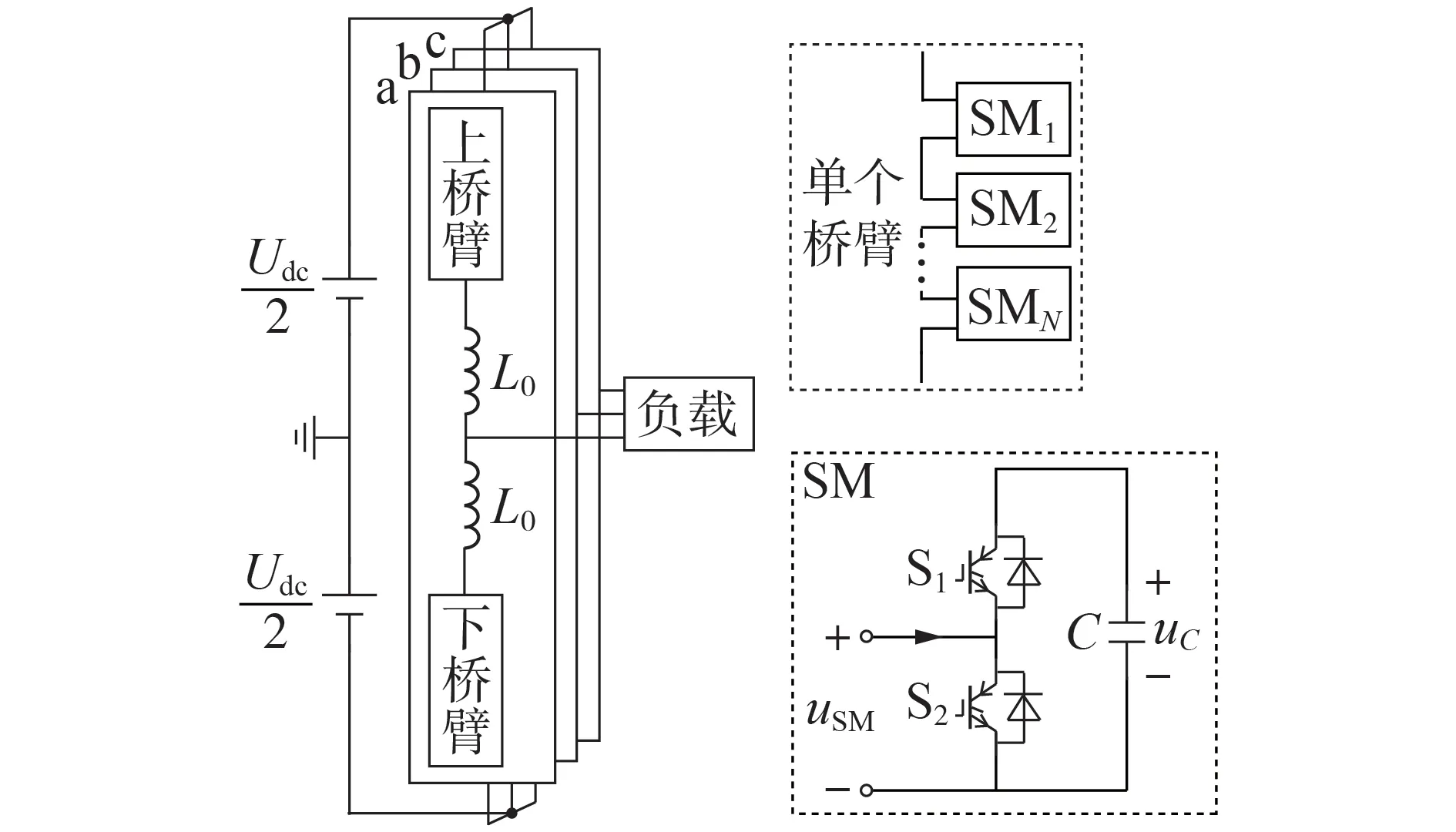
图1 MMC逆变器拓扑结构Fig.1 Topology structure of MMC inverter

SM 正常运行时，S1、S2的驱动信号互补，分为投入和切除2 种运行模式。在投入模式下，S1导通、S2关断，根据电流方向的不同，电容分别进行充、放电，此时uSM≈uC；在切除模式下，S1关断、S2导通，uC几乎保持不变，uSM=0。SM 的运行模式由调制策略和电容电压平衡方法共同决定。对于多电平变换器，目前有空间矢量调制、特定次谐波消除、最近电平逼近和载波移相PSC（Phase-Shifted Carrier）等多种调制方式。相比于其他调制策略，载波移相调制技术具有实现简单、等效开关频率高及谐波特性良好等优点。在基于PSC 的脉宽调制PWM（Pulse Width Modulation）（PSC-PWM）策略中，每个桥臂的N个SM对应1个特定的正弦调制波和N个依次错开2π/N相位角的三角载波，通过调制波与三角载波比较得到的N组PWM 信号来驱动N个SM，各uSM相加便可得到单个桥臂的输出电压。此控制策略下，可以通过调节各SM的参考信号来实现电容电压平衡，具体的实现方式参考文献［11］。

1.2 故障参量信号的选取

由于多个开关管同时故障的概率非常低，通常只考虑单个开关管故障的情况，则开关管故障可分为S1开路故障和S2开路故障2 种。S1开路故障会影响SM 的投入模式，使原本进行充、放电的电容进入旁路状态；S2开路故障会影响SM 的切除模式，使原本处于旁路状态的电容进入充、放电状态。某一SM的S1、S2开路故障会导致该SM 的电容异常充放电、产生不正常的波动，进而偏离预期值。采用PSCPWM 策略时，每一相可以单独控制，其他相的uC不会受故障相的影响，因此可以单独分析各相SM开关管故障，将单相SM 的uC作为区分故障开关管的故障参量信号。

1.3 故障参量信号的耦合性分析

由于MMC 为非线性系统，各控制变量与状态变量之间具有强耦合性，同相其他非故障SM的电容电压也会受到故障SM 的影响而偏离预期值。在一个每相含有6 个SM 的MMC 中，a 相中各SM 电容电压由上至下分别记为uC1、uC2、…、uC6。图2 由上至下3个子图依次为MMC 上桥臂开关管SM1的S1、SM1的S2、SM2的S1在0.6 s 发生开路故障的uC变化曲线。经对比MMC 上桥臂开关管SM1的S1、SM1的S2开路故障的uC变化曲线发现，同一SM 中的不同开关管故障后参量信号的变化趋势不同，故障特征明显；经对比MMC 上桥臂开关管SM1的S1、SM2的S1开路故障的uC变化曲线发现，尽管故障SM 与非故障SM 的电容电压之差会随时间逐渐增大，但在故障刚发生后的几个周期内，不同SM在同一位置的开关管故障参量信号变化趋势相似，故障特征不够明显。此时，由于故障SM 与非故障SM 参量信号之间的差值较小，基于模型的故障诊断方法难以设置合适的故障阈值，需要花费一定的时间才能正确定位故障开关管。基于传统机器学习的方法需要人工提取信号中关键的非耦合性特征，而参数不同的系统其关键特征也会有所不同，整个过程需要经过大量的实验。因此，本文利用SE-DSCNN，在网络学习的过程中自动提取各故障参量信号中具有代表性的特征信息，以减少人工提取特征的工作量，提高故障诊断效率，能够在故障早期准确判断故障类型。

图2 不同开关管故障时各电容电压的对比Fig.2 Comparison of capacitor voltages among different switch faults

2 基于SE-DSCNN的故障诊断方法

为了从具有耦合性的参量信号中提取深层次特征，同时满足计算量小、准确率高的诊断要求，基于卷积神经网络（CNN），用深度可分离卷积（DSC）代替标准卷积以提取信号中的特征信息同时减少计算量，结合SE模块突出具有代表性的特征信息。

2.1 CNN基本理论

CNN 是一种使用卷积运算的前馈神经网络，通常由以下几种类型层组成。

式中：θ为需要学习的模型参数。

2.2 DSC原理

为了减少网络的参数量、提高网络的运行速度，小型高效的神经网络逐渐成为当前的研究热点之一。MobileNet［12］就是轻量卷积神经网络的一个代表，其核心组成部分为DSC。将DSC 应用于多电容电压时间序列分类问题中，不仅可以大幅减少网络参数量，还可以将多电容电压时间序列的时间相关性和跨通道相关性解耦。

DSC 将标准卷积分解成逐通道卷积和逐点卷积2 个部分，如附录A 图A1（a）所示。首先，逐通道卷积给每个输入通道分配一个单独的过滤器，分别映射各通道序列的时间相关性。然后，逐点卷积执行1 × 1 卷积，生成逐通道卷积输出量的线性组合，以映射不同传感器的跨通道相关性。通过以上2 个独立的步骤，时间相关性和跨通道相关性可以被充分解耦。用式（6）、（7）来表示以上2个步骤。

2.3 SE模块原理

CNN 同时提取空间和通道中的特征信息，其卷积层输出的特征映射包含不同程度的代表性信息，越具有代表性的特征所包含的有用信息就越多。为了突出通道中具有代表性的特征，文献［13］提出了一种名为SE 模块的网络结构，通过评估通道特征的信息量来学习特征权重，在增大有用特征权重的同时降低无用特征权重，从而实现通道特征的自适应校准。具体而言，通道特征的自适应校准分为2 步实现，包括挤压操作和激励操作，如附录A图A1（b）所示。

首先，挤压操作通过全局平均池化，将上一卷积层所有输出通道的全局信息xl∈R1×W×Ct压缩成一个通道描述符ul∈RCt，ul中第c个通道的元素为：

2.4 SE-DSCNN的结构框架

本文将SE 模块与DSCNN 相结合，网络结构如图3 所示，输入为各电容电压，输出为状态标签。首先将各电容电压输入第一个DSC 层，以提取全局核心特征；接着利用第二个DSC 层和SE 模块来提取各通道的有效特征，为了同时保留全局特征和局部特征，使用残差连接将上一卷积层的输出与SE 模块的输出相连；将提取到的特征输入第三个DSC 层以提取更多的特征信息；最后展平（Flatten）层将所有的特征展开，再通过全连接（Dense）层与Softmax 分类器相连。其中，每个DSC 层与激活函数ReLU 之间进行了批归一化BN（Batch Normalization）处理，其作用是提高网络的泛化能力以及加快网络的训练速度；丢弃（Dropout）层在训练过程中以一定的概率从神经网络中随机丢弃神经元，是一种防止过拟合的正则化方法；为了实现下采样，需要在DSC层之后使用最大池化（Max Pooling）层及平均池化（Average Pooling）层。

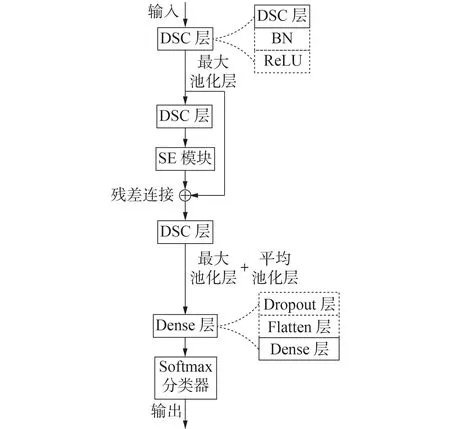
图3 SE-DSCNN的结构Fig.3 Structure of SE-DSCNN

2.5 基于SE-DSCNN的故障诊断流程

基于SE-DSCNN 的MMC 开关管故障诊断流程如图4所示，具体步骤如下。

图4 基于SE-DSCNN的故障诊断流程Fig.4 Flowchart of fault diagnosis based on SE-DSCNN

1）数据采集。改变运行条件，模拟各开关管分别故障的情况，采集各电容电压传感器从正常到故障的数据，将数据分段并归一化后得到样本数据。

2）数据处理。首先通过滑动时间窗口将数据分段，即利用大小一定、步长一定的滑动窗口按时间顺序将每个通道序列的数据划分成各个小片段；接着对分段后的样本做归一化处理，由于故障发生后，电容电压会逐渐偏离正常值，为了消除局部幅值变化的影响、突出样本的主要特征，根据式（11）将各通道的样本数值控制在［0，1］的范围内。

式中：X和X＇分别为原始数据和归一化后的数据；Xmin和Xmax分别为数据X中的最小值和最大值。

3）设置标签。单桥臂含有N个SM 的单相MMC开关管总数为4N，将正常状态的标签设置为0，开关管故障状态的标签从上到下设置为1、2、…、4N。时间窗口在滑动时会经历正常状态过渡到故障状态的阶段，这个阶段称为过渡时期。过渡时期的样本标签通过“大多数原则”来确定，即样本片段中占比最高的状态为样本标签。以大小为2 个自然周期的时间窗口为例，绘出数据分段及标签设置的过程，如附录A 图A2所示。其中，故障点前一个周期和后一个周期分别用“-1”和“+1”表示，其他周期的表示方法依此类推，则滑动时间窗口起点在“-2”和“-1”期间取得的样本处于过渡期间，将起点在“-2”期间内样本标签设置为0、起点在“-1”期间内的样本标签设置为1、2、3、…、4N。

4）训练阶段。训练阶段的数据集包含样本片段及样本标签，随机划分为训练集和验证集，训练集用于训练分类网络，验证集用于评估模型效果，训练得到最优模型。

5）测试阶段。将测试阶段的样本片段输入训练阶段得到的最优模型，该模型自动提取片段特征并输出测试片段的预测标签。

3 数据获取及模型设置

3.1 样本数据获取

为了验证所提方法的可行性，根据图1 的拓扑结构在MATLAB／Simulink 的环境中搭建仿真系统，参数如附录A 表A1所示。为了采集不同运行条件下的故障数据，需要改变故障发生时间。设故障起始时间为2 s，以2 ms 的步长在一个20 ms 的周期内设置10 种时间偏移量，即Δ1=0，Δ2=2 ms，…，Δ10=18 ms，则10种故障发生时间为2 s+Δi（i=1，2，…，10）。额定负载下，改变10 种故障发生时间，得到上桥臂SM1中S1、S2故障后10 个周期的各电容电压波形图分别如附录A 图A3（a）、（b）所示。从图中可以看出，由于故障发生时间的不同，故障点的起始电容电压不同，波形有细微的差别，但都属于同一种故障类型。模拟12 种开关管故障情况，每种情况下设置10 种故障发生时间，重复10 次运行，每次随机改变负载值（波动范围在±20%之内），以50 kHz 的采样频率采集故障点前3 个周期及后10 个周期的6 个电容电压信号，则一共得到1200组数据。

3.2 模型参数设置

基于图3 所示结构，将网络的参数设置如下：卷积核的大小为1×13，移动步长为1，3 个DSC 层中核的数量分别为16、32、64，SE 模块中的缩放参数r为8，最大池化层的大小为1×3，平均池化层的大小为1×8，丢弃率设为0.2，具体的结构及参数见附录A表A2。与其他的深度学习模型相似，该模型也可以通过通过梯度下降和反向传播算法进行训练。训练时，将预测状态标签和真实状态标签之间的交叉熵作为损失函数，并使用Adam 优化算法［14］来最小化损失函数。每次训练的样本数目设为128，训练集与验证集之比为4∶1，最大迭代次数设置为500。同时设置提前结束训练的条件：若连续20 次迭代中验证集的损失函数不下降，则停止训练。

3.3 时间窗口设置

时间窗口的大小和步长会直接影响样本中特征信息的含量、诊断的时间延迟、检测到故障的时间点。通常时间窗口越大，每个样本包含的特征信息越多，诊断的精度越高，但诊断的总时间会相应延长，所需要的内存空间也越大；滑动步长越小，检测到故障的时间点越精准，对数据传输和硬件内存的要求也越高。为了充分提取各电容电压所包含的特征信息，样本应至少包含正常或故障状态下的1 个完整周期。经权衡考虑，将滑动时间窗口的大小和步长分别设置为2 000、100，则3.1 节中每组数据分段后可得到111 个样本，总样本数为133 200。再按4∶1 的比例随机划分数据集，训练阶段有106 560 个样本，测试阶段有26640个样本。

4 结果分析

4.1 模型的评价指标

4.1.1 分类效果的评价指标

由于采集到的每组数据包含3 个周期的正常数据和10 个周期的故障数据，正常类别的样本数量和故障类别的样本数量不完全相等。因此，除了准确率之外，本文还使用了混淆矩阵、宏查准率、宏查全率、宏F1等指标来衡量模型的分类效果。

混淆矩阵M中的元素mi，j表示类型i的样本被预测成类型j的数量。则准确率A1的定义为：

4.2 模型的整体诊断效果

根据第3 节获取的样本数据及设置的模型参数，使用SE-DSCNN重复10次实验，每次实验都重新随机划分训练集、验证集和测试集。将10 次测试集片段分类结果汇总，画出标准化后的混淆矩阵，如附录A 图A4所示。从图中可以看出，大部分的误报率都集中在正常片段与故障片段的分类，这主要是处于过渡时期样本所造成的混淆。此外，故障类型之间的误报率主要集中在处于同一位置上的开关管，从图2 可以看出同一位置上的开关管在故障刚发生的1 个周期内，各电容电压的变化曲线几乎完全重合，这造成了故障类型1、3、5 和故障类型7、9、11 之间的分类出现了极小的偏差。但总体而言，故障与故障之间的区分效果较好，绝大部分的故障都能被模型正确识别。

将基于SE-DSCNN 的诊断方法与其他几种基于机器学习的多电平变换器诊断方法进行对比，包括文献［8-10］的方法。重复10 次实验取平均值，得到各方法在A1、Pmacro、Rmacro、Fmacro这4 个指标上的测试样本结果，如表1 所示，其他4 种诊断方法的相关参数设置和标准化混淆矩阵结果分别见附录A 表A3和图A5。经尝试发现：方法1 无法处理第3 节的样本规模，文献［8］使用mRVM 进行故障诊断的样本只有450 个，此处将样本数量压缩到原来的1/10，方法1 的分类结果不太理想，说明mRVM 无法处理规模较大的样本；方法2 的几个分类指标达到了90%以上，但观察混淆矩阵后发现各类别的查全率差距非常大，说明SVM 只能区分特定的类别；方法3通过PCA提取的主成分数量比文献［9］更多，说明本文的数据特征没有文献［9］的数据特征明显。方法1—3在文献［8-9］中使用的样本都没有经过滑动时间窗口分段，而是将较长时间范围内的数据作为一个样本，包含了特征明显的故障后期数据，所以诊断准确率较高。但本文所采用的数据不仅有特征明显的故障后期样本片段，还有特征不够明显的故障早期样本片段。在这种情况下，这3 种方法都很难区分不同类型的故障，即使是对特征明显的故障分类也会产生混淆。方法4 出现误报率的主要原因来自处于同一位置的开关管，比如故障类型1、3、5 之间和故障类型2、4、6 之间出现混淆，说明SSAE 区分耦合性特征的效果很差。方法4 对处于不同位置的开关管分类并不会出现偏差，而前3 种方法会出现误报，说明自动特征提取在区分明显特征时比人工特征提取的效果更好。经对比发现，本文所提基于SE-DSCNN的诊断方法在包含耦合性特征的总样本上的整体分类效果远好于其他4 种诊断方法，可以实现早期故障诊断。

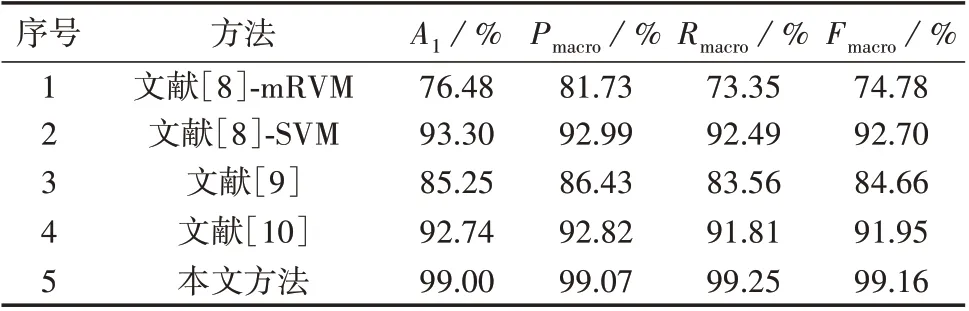
表1 不同诊断方法的结果对比Table 1 Comparison of different diagnostic methods

4.3 故障早期的诊断效果

为了研究所提网络在故障早期的诊断效果，并且验证模型的改进效果，将SE-DSCNN 与其他3 个深度学习分类网络进行对比，分别是DNN、CNN、DSCNN。DNN 是只包含Dense 层的深度学习网络，CNN 和DSCNN 已第2节中介绍。这3种网络的核心层（Dense 层或卷积层）数量与SE-DSCNN 相同，均为3个，具体结构及参数见附录A表A4—A6。

通过模拟12 种故障情况，随机改变故障发生时间及负载50 次，得到600 条运行记录。取每条记录中故障点前10个周期和后10个周期进行分析，以滑动窗口起点所在的1 个周期为单位，计算出各网络在不同时期的准确率，如附录A 表A7所示。从表中可以看出，正常时期的分类准确率为100%，说明几个深度学习网络在正常时都不会出现误诊的情况。

为了进一步分析网络诊断不同故障类型的效果，按照4.1.2 节的定义，计算出各网络在故障发生后不同时期的诊断正确率，其具体数值及网络参数量见表2，表中“-2”、“-1”、“+1”、“+2”、“+3”分别表示滑动时间窗口中的样本分别包含了故障发生后第1—5个周期的数据。从表中可以看出：所提网络的分类性能最好，故障刚发生后的2 个过渡时期的诊断正确率在99%以上，此后的诊断正确率均达100%；其他网络在故障发生后，诊断正确率会先下降再上升，有2～3 个周期的误诊率较高。相比于DNN 和CNN，SE-DSCNN 的参数量大幅减少，这是DSC 发挥的作用。SE-DSCNN 的模型参数量比CNN的参数量减少了70.92%左右，但诊断性能却得到了小幅度提升；DSCNN 在故障发生后第2 个和第3 个周期的诊断正确率均不到90%，诊断性能远不如SE-DSCNN，无法正确识别早期故障。这说明了SE模块对网络性能有较大的提升效果。