部分充填砼钢箱连续组合梁抗裂性能分析

2022-05-11莫时旭邹泽群郑艳

华侨大学学报（自然科学版） 2022年3期

莫时旭，邹泽群，郑艳

(1.桂林理工大学土木与建筑工程学院，广西桂林 541004；2.桂林理工大学广西岩土力学与工程重点实验室，广西桂林 541004)

钢-混凝土组合梁具备质量轻、承载能力高、施工便利等优点，在桥梁工程中应用广泛.但钢-混连续组合梁存在负弯矩区桥面板开裂和钢梁受压失稳等问题.在负弯矩区截面下缘布置混凝土板形成双重组合梁是改善连续组合梁中支座区受力性能的有效措施之一[1].该措施能显著提高组合梁的整体刚度和承载能力，但对负弯矩区桥面板裂缝控制能力的提高作用有限[2-3].

高强度、高性能材料的应用是桥梁结构发展的趋势之一[4].超高性能混凝土(UHPC)具有超高强度、超高塑性及韧性、高裂纹自修复性和良好的施工性.UHPC材料在结构高拉应力区的使用为桥梁裂缝控制提供了一条新的可行途径.目前，许多学者开展了UHPC抗裂性能的研究.Charron等[5]对受拉UHPC棱柱体试件透水性进行研究，表明当拉应变小于0.15%时，试件出现分布裂缝，但不影响试件的耐久性；Hu等[6]开展钢-UHPC、钢-混组合梁的抗弯试验，发现试件的最大裂缝宽度减少59%，开裂荷载和极限承载力分别提高了3.4倍和26%；刘新华等[7]研究3种不同负弯矩区接口形式的钢-UHPC组合梁的受力性能；邵旭东等[8]研究构件参数对钢-UHPC轻型组合桥梁的影响，发现UHPC厚度和栓钉间距对开裂应力影响不大.

综合考虑材料的发挥程度和经济性等因素，本文采用UHPC部分或全部替代连续梁中支座区翼板中的普通混凝土(NC)，形成UHPC翼板-部分充填砼钢箱连续组合梁.利用ABAQUS软件对UHPC翼板-部分充填砼钢箱连续组合梁的受力全过程进行有限元模拟，分析UHPC的本构关系、翼板分布长度、UHPC填充厚度、配筋率等关键参数对该组合梁受力性能的影响.

1 NC翼板-部分充填砼钢箱连续组合梁试验

1.1 试验方案

开展3根两跨NC翼板-部分充填砼钢箱连续组合梁(简称NC翼板连续组合梁)静载试验，试件编号为PFSCB1～PFSCB3.试验梁长6 400 mm，翼板宽1 000 mm，厚120 mm，钢箱高300 mm；栓钉直径13 mm，高100 mm；纵筋直径12 mm，分布筋直径8 mm.3根NC翼板连续组合梁试件的参数，如表1所示.表1中：ρ为翼板配筋率；η为抗剪连接度；n，s分别为负弯矩区栓钉的数量和间距.NC翼板连续组合梁的构造图，如图1所示.

表1 3根NC翼板连续组合梁试件的参数

(a)加载立面图 (b)负弯矩区截面

混凝土和钢材的材料特性，如表2，3所示.表2，3中：fc，Fl，fc，Fi分别为翼板混凝土、钢箱内填混凝土的抗压强度；D为钢筋直径；h为钢板厚度；Es为弹性模量；fy为屈服强度；fu为抗拉强度.

表2 混凝土的材料特性

表3 钢材的材料特性

1.2 试验结果与分析

1.2.1 荷载-跨中挠度曲线 NC翼板连续组合梁的荷载(P)-跨中挠度(w)曲线，如图2所示.由图2可知：在加载初期，组合梁处于整体弹性阶段，荷载-跨中挠度呈线性关系，斜率较大；荷载继续增大，中支座负弯矩区翼板出现横向裂缝，试验梁进入开裂后弹性工作阶段；随着荷载的增大，跨中钢箱底板开始屈服，组合截面中性轴逐渐上移，混凝土翼板底面开始受拉开裂；最后，试验梁进入承载力极限状态，破坏时的承载力则取决于混凝土顶板极限压应力和钢箱底板极限抗拉强度.

图2 NC翼板连续组合梁的P-w曲线图3 NC翼板连续组合梁的P-Wmax曲线

1.2.2 荷载-最大裂缝宽度曲线 NC翼板连续组合梁的荷载-最大裂缝宽度(Wmax)曲线，如图3所示.由图3可知：翼板配筋率对开裂荷载影响不大，对最大裂缝宽度影响较大；当荷载达到300 kN以后，试件PFSCB1的最大裂缝宽度迅速增大，并超过0.20 mm；试件PFSCB2的最大裂缝宽度与试件PFSCB1相比明显减小，但略大于PFSCB3，当荷载达到450 kN后，试件PFSCB2的最大裂缝宽度超过0.20 mm；当荷载达到650 kN后，试件PFSCB3的最大裂缝宽度逐渐超过0.20 mm.

2 UHPC翼板-部分充填砼钢箱连续组合梁

虽然提高NC翼板配筋率对控制最大裂缝宽度的发展有一定的作用，但翼板配筋率为2.0%的试件PCSCB3在弹性工作阶段的裂缝宽度仍超过0.20 mm，不能满足结构耐久性要求.目前，连续组合梁裂缝控制的常用措施有两种：一是通过张拉预应力筋施加预应力，但受钢梁的约束，预应力效率较低；二是通过施工措施形成预压应力，如支座顶升法、跨中配重法等，但该方法形成的预应力有限.

UHPC与普通混凝土间存在良好的粘结力，可以在弯拉下协调变形，使两者交界面较难发生相对滑移[9-10].因此，将UHPC应用于连续组合梁翼板是预应力技术之外的裂缝控制途径.基于此，提出在NC翼板-部分充填砼钢箱连续组合梁中支座区的翼板中部分采用UHPC材料，跨中翼板采用NC材料.基于UHPC材料性能已有的研究成果，通过有限元分析方法初步分析UHPC翼板-部分充填砼钢箱连续组合梁的受力性能.

3 部分充填砼钢箱连续组合梁有限元分析

3.1 单元选取

钢板、混凝土、栓钉、加劲肋均使用线性3维8节点实体单元C3D8R.混凝土、钢梁的网格尺寸均为20 mm×20 mm×20 mm，栓钉的网格尺寸为6.5 mm×6.5 mm×6.5 mm.钢筋采用2节点3维桁架单元T3D2，网格尺寸为20 mm×20 mm×20 mm.组合梁的1/4有限元模型，如图4所示.

图4 组合梁的1/4有限元模型

3.2 材料参数

3.2.1 混凝土 C40混凝土的弹性模量Ec=32.5 GPa，泊松比μ=0.2，选择ABAQUS损伤塑性(CDP)模型进行模拟.相关参数均按推荐取值[11-12]：剪切角为30°，偏心率为0.1，屈服应力比为1.16，屈服常数为0.666 7，黏性系数为0.000 5.混凝土本构采用GB 50010-2010《混凝土结构设计规范》[13]的应力-应变曲线.

根据抗拉强度是否大于弹性抗拉强度，将UHPC分为应变软化、低应变强化、高应变强化3种类型[14].3种类型UHPC的抗压强度上升段基本一致，下降段有一定区别，但区别不大[15].文中主要使用UHPC抵抗开裂，因此，将其简化为受压本构模型.3种类型UHPC对应的弹性模量Ec分别为36.8，36.4，40.6 GPa[16]，泊松比μ=0.2，选择ABAQUS损伤塑性模型，相关参数与普通混凝土一致.

参照瑞士UHPC的设计规范[17]，受拉应力(σt)-应变(ε)关系表达式为

(1)

式(1)中：fct为弹性极限抗拉强度，3种类型UHPC对应的fct分别为7.7，8.4，10.0 MPa[16]；εpc为极限应变；εca为弹性阶段峰值应变，3种类型UHPC对应的εca分别为2.0×10-4，2.3×10-4，2.5×10-4[16].

受压本构关系采用文献[18]提出的UHPC受压应力-应变曲线，无量纲后得

(2)

式(2)中：A=Ecε0/fc，ε0= 3.36×10-3，fc=133.3 MPa[18]，A=1.07；B= 2.41.

由式(1)，(2)可得UHPC本构关系曲线，如图5所示.

(a)应变软化受拉曲线 (b)低应变强化受拉曲线 (c)高应变强化受拉曲线 (d)受压应力-应变曲线

3.2.2 钢材和栓钉钢材的应力-应变采用双折线强化塑性模型，即

(3)

式(3)中：εy，εt，εu分别为钢材的屈服应变、强化应变、极限应变.

栓钉的应力-应变采用三折线模型[19]，即

(4)

3.3 有限元模型的建立

将钢梁-翼板、填充混凝土-钢梁箱室的法向接触面定义为“hard”接触，切向接触面定义为罚函数接触，对应的摩擦系数分别为0.4[20]，0.6[21].栓钉底端与钢梁使用“Tie”固结约束，并以“Embedded”命令嵌入翼板内.

考虑到结构及加载的对称性，沿桥纵、横向建立1/2模型，从而建立1/4有限元分析模型以提高计算效率，对称边界面约束转动和法向位移.支座设置刚性垫块，在垫块支承线上按实际支承情况进行相应位移约束，集中荷载通过弹性模量较大的刚性垫块施加到梁体上.

3.4 有限元模型的验证

3.4.1 裂缝特征试件PFSCB2的负弯矩区翼板裂缝发展，如图6所示.由图6(a)可知：裂缝首先出现在翼板中支座附近，随着荷载的增加，裂缝逐渐向跨中发展，在跨中附近呈现C字型分布.由于ABAQUS塑性损伤模型无法模拟裂缝，故通过应变云图(图6(b))观察裂缝分布规律，可知其与实测裂缝发展分布规律相似.

(a)裂缝分布(裂缝出现顺序为黑、红、蓝) (b)抗拉塑性应变云图

3.4.2 试验值与模拟值的对比对NC翼板连续组合梁进行数值模拟，并与相应的试验结果对比，如图7所示.图7中：Δ为滑移；d为距中支座的距离.

(a)荷载-跨中挠度曲线 (b)纵向滑移曲线

主要参数的试验值与模拟值的对比，如表4所示.表4中：Pcr为开裂荷载；Pu为极限荷载；Δmax为最大纵向滑移；Δmin为最小纵向滑移；δ1，δ2，δ3，δ4分别为开裂荷载、极限荷载、最大纵向滑移、最小纵向滑移的试验值与模拟值的相对误差.

表4 主要参数的试验值与模拟值的对比

综上可知，试验梁的裂缝特征、荷载-跨中挠度曲线、纵向滑移曲线与有限元模拟结果均吻合良好，验证了有限元模型的适用性.由于UHPC翼板-部分充填砼钢箱连续组合梁的建模方法、尺寸与NC翼板-部分充填砼钢箱连续组合梁相同，因而也适用该有限元模型.

4 UHPC翼板连续组合梁结构参数分析

以开裂荷载、极限荷载最大为优化目标，探究UHPC本构关系、负弯矩区UHPC替换长度、填充厚度、配筋率等关键设计参数对组合梁受力性能的影响.

UHPC的开裂荷载可分为初裂荷载和可视开裂荷载.初裂荷载是翼板拉应变达到材料弹性极限应变时的荷载，UHPC翼板的初裂应变为2×10-4[16]，NC翼板的初裂应变为8×10-5.可视开裂荷载定义为最大裂缝宽度达到0.05 mm[22]时的荷载.通过直接拉伸试验得到应变软化、低应变强化、高应变强化UHPC对应的可视开裂应变分别为6.0×10-4，1.1×10-3，2.0×10-3[16，23].NC翼板的可视开裂荷载约等于初裂荷载.有限元分析的标准梁参数如下：中支座区UHPC翼板长3 600 mm，厚120 mm，配筋率为1.5%；UHPC本构为高应变强化型.

4.1 UHPC本构关系

UHPC本构分为应变软化(UO)、低应变强化(UA)、高应变强化(UB)3种类型.不同本构关系对比结果，如图8所示.

(a)荷载-跨中挠度曲线 (b)翼板本构关系变化分析

由图8可知：UO，UA，UB三者的荷载-跨中挠度曲线区别不大，而可视开裂荷载增长显著；当P=0.5Pu时，在相同配筋率下，UB翼板组合梁的割线刚度为150.7 kN·mm-1，比NC翼板组合梁(割线刚度为137.1 kN·mm-1)提高了10%，初裂荷载提高了约2.3倍，极限荷载提高了约12.3%；若考虑UB优异的裂缝宽度控制能力，则其可视开裂荷载较普通混凝土的初裂荷载提升7.6倍.

4.2 UHPC替换长度

由于UHPC造价较高，应在满足结构受力的条件下，尽量减少UHPC的用量.但是仅在部分负弯矩区铺设UHPC会导致交界面普通混凝土先于UHPC拉裂.因此，需要筛选出负弯矩区UHPC达到初裂荷载甚至可视开裂荷载时，交界面普通混凝土尚未开裂的UHPC替换长度.UHPC的几何尺寸，如图9所示.图9中：l为计算跨径，l=3 000 mm；2al为两跨连续梁的UHPC替换长度，a为长度系数.

(a)立面图 (b)负弯矩区截面

不同UHPC替换长度下的P-w曲线，如图10所示.UHPC替换长度变化分析，如图11所示.

图10 不同UHPC替换长度下的P-w曲线图11 UHPC替换长度变化分析

由图11可知：当长度系数a从0.10增加到1.00时，UHPC翼板连续组合梁的刚度、极限承载力均有显著提高；当a<0.25时，交界面普通混凝土会先于负弯矩区UHPC开裂，翼板的可视开裂荷载约等于初裂荷载；当a增加到0.30时，翼板的可视开裂荷载大于屈服荷载；当a继续增加到0.60时，翼板的屈服荷载、极限荷载均有较大提升.综合考虑经济因素和受力性能，选择a=0.30，即UHPC替换长度2al=1 800 mm(0.3倍计算跨径)较为合适.

4.3 UHPC填充厚度

当负弯矩区UHPC翼板长度为1 800 mm时，模拟分析不同UHPC填充厚度(H)下的P-w曲线，如图12所示.UHPC填充厚度变化分析，如图13所示.

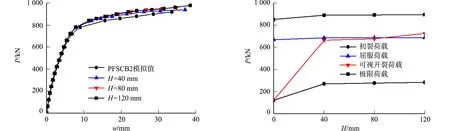
图12 不同UHPC填充厚度下的P-w曲线图13 UHPC填充厚度变化分析

由图13可知：当UHPC填充厚度从40 mm增加到120 mm时，翼板的初裂荷载、极限荷载分别增加了4.9%，0.4%，增长幅度较低.虽然UHPC填充厚度为40 mm时的可视开裂荷载小于屈服荷载，但是仅减少3.2%，能满足负弯矩区翼板裂缝控制的功能.因此，从经济角度考虑，选择UHPC填充厚度为40 mm(1/3翼板厚度)更加合理.

4.4 翼板配筋率

在连续组合梁中，受拉纵筋能有效抑制裂缝的产生和发展，显著提高组合梁的极限承载力和延性.当UHPC翼板长度为1 800 mm，填充厚度为40 mm时，不同翼板配筋率下的P-w曲线，如图14所示.翼板配筋率变化分析，如图15所示

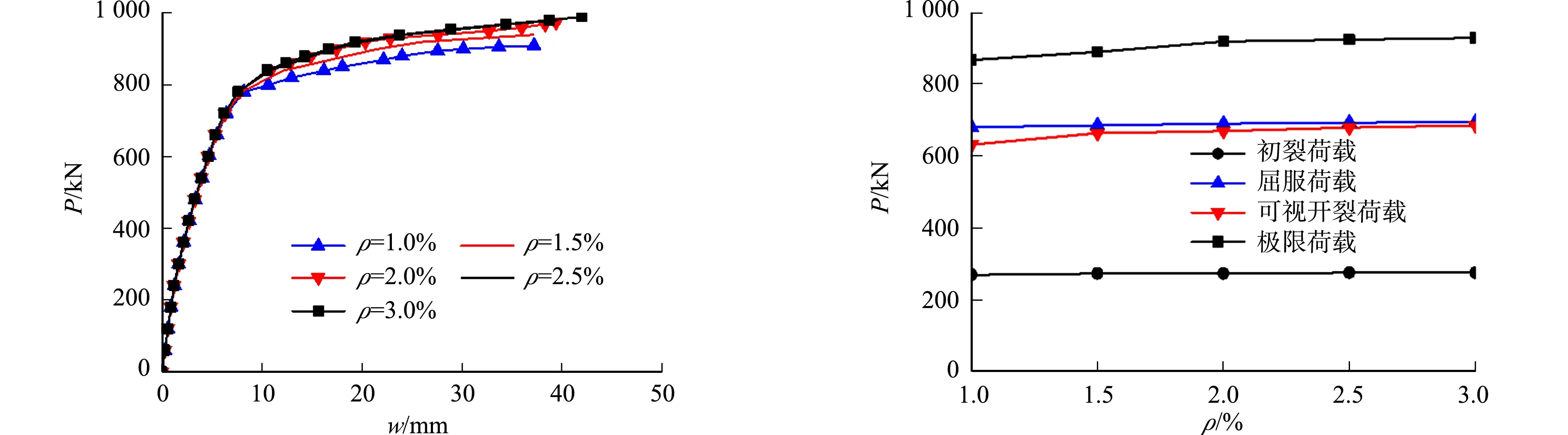
图14 不同翼板配筋率下的P-w曲线图15 翼板配筋率变化分析

由图15可知：当翼板配筋率从1.0%增加到1.5%时，翼板的初裂荷载、屈服荷载、可视开裂荷载、极限荷载分别提高了1.1%，0.6%，5.3%，2.3%，此后，增长幅度逐渐降低；当配筋率从1.5%增加到2.0%时，翼板的初裂荷载、屈服荷载、可视开裂荷载、极限荷载分别提高了0.1%，0.7%，0.9%，3.2%，前3项的增长幅度几乎趋近于零.虽然配筋率为1.5%～2.0%时翼板的可视开裂荷载小于屈服荷载，但都只降低3.0%左右，能够满足抗裂要求.综合考虑，选取翼板配筋率为1.5%～2.0%较经济合适.