采用MEA-AdaBoost-BP模型的工程结构可靠性分析方法

胡启国，李致明

(重庆交通大学 机电与车辆工程学院，重庆 400074)

在实际工程运用中，需要运用可靠性分析来预先评估机械结构的可靠指标.但结构工程实际可靠性分析中结构功能函数隐性表达，传统的分析方法如一次二阶矩[1]、二次二阶矩[2]法、蒙特卡洛(Monte-Carlo)[3]和基于代理模型思想的响应面[4]可靠性分析法，都存在计算时间长，精度受限等缺点，不能更好地进行可靠性指标求解.随着人工神经网络的发展，将神经网络算法应用于结构可靠度计算，有效避免了传统结构隐性功能函数，提高了可靠度计算精度.

随着结构工程可靠性算法的发展，Deng等[5]采用前馈神经网络，以最小的计算量逼近隐性功能函数和函数导数，有效应用于隐性功能函数的极限状态可靠性求解；温凯等[3]采用模拟退火(SA)优化神经网络阈值和权值，再用神经网络逼近隐性功能函数；姜逢源等[6]将AdaBoost算法与BP神经网络算法结合逼近隐性功能函数，进行板桩结构极限状态下的可靠性求解.这些方法为工程结构隐性功能函数可靠性求解提供了有益借鉴，但其对神经网络单一的优化，使构建的功能函数还具有局限性和误差性.

实际工程中结构功能函数无法显性表达，在利用BP神经网络算法时，必须避免算法出现过拟合和预测精度低的缺点.因此，针对此缺点，本文运用思维进化算法(MEA)的群体特性，提出基于MEA-AdaBoost-BP神经网络算法模型的可靠性求解方法.

1 MEA-AdaBoost-BP算法模型

1.1 思维进化算法

思维进化算法(MEA)是基于趋同和异化操作特性和记忆多代信息的特点，得到全局最优个体的一种群体寻优算法.在初始阶段，迭代生成相应大小的个体.根据得分，得到优秀的和临时的得分最高的个体.通过结构的并行性，在几个最优个体周围生成局部最优子群，在临时个体周围生成局部临时子群.然后，通过趋同和异化，构建上一代和优于上一代的子群体，将得分最高的个体视为全局最优个体.思维进化算法(MEA)流程图，如图1所示.

图1 思维进化算法(MEA)流程图

目前，MEA-BP神经网络算法模型优点在于运用思维进化算法(MEA)趋同和异化操作智能搜索全局最优个体，避免BP神经网络的局部搜索的缺点；同时，运用解码规则得到最优权值和阈值，避免BP神经网络局部预测精度差的问题.综上，基于文献[7]搭建了MEA-AdaBoost-BP神经网络算法模型，实现了对BP神经网络的全局优化.

1.2 AdaBoost-BP神经网络

初始时，BP神经网络经过训练得到随机初始权值和阈值，形成T个权重一致的弱预测器函数，再用AdaBoost算法将弱预测器反复迭代t次；每次迭代后预测，若预测结果误差大于设定误差，则赋予该组样本较大权重进行加权学习.最终由AdaBoost算法进行加权组合T组BP神经网络弱预测器，形成AdaBoost-BP强预测函数.AdaBoost-BP算法流程图，如图2所示.

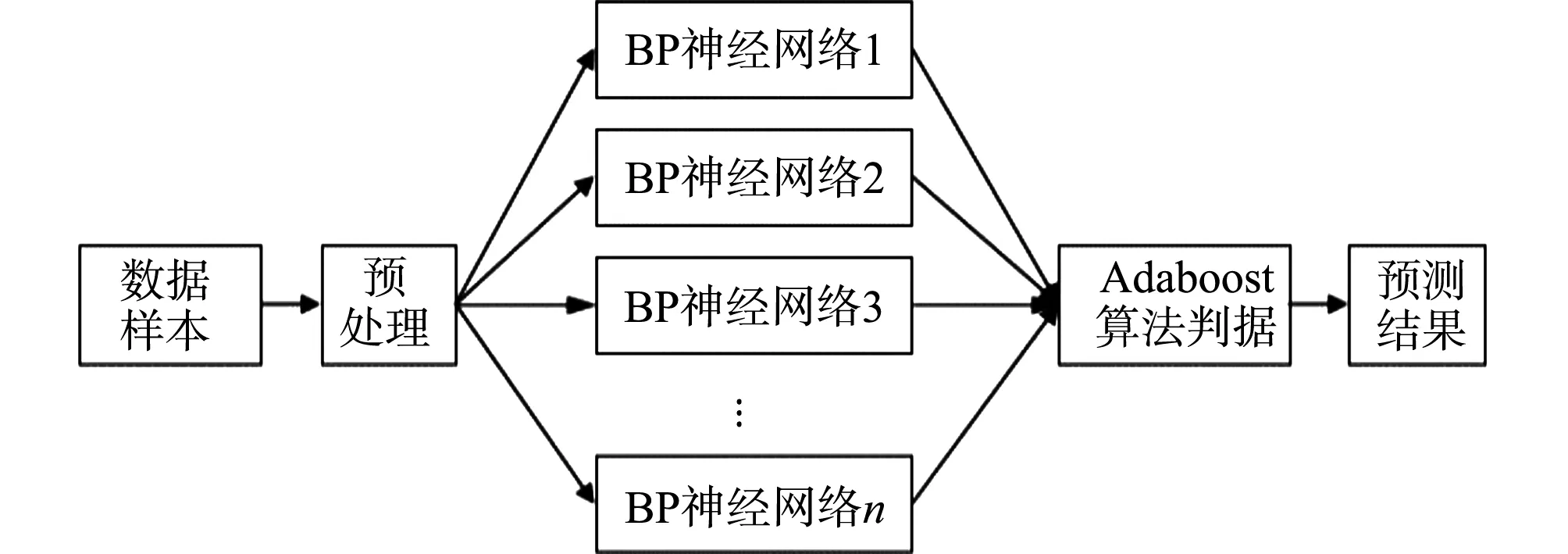
图2 AdaBoost-BP算法流程图

AdaBoost-BP神经网络算法有如下4个具体的操作步骤.

步骤1数据初始化.随机选择M组训练数集，运用已优化权值和阈值的BP神经网络构造T个弱预测器，并赋予相同的初始分布权值，即Dt(i)=1/M，i=1，2，…，M；t=1，2，…，T.

步骤3权重预测与调整.如果预测误差和et大于设定的误差，根据权重Dt(i)计算调整下一个权重Dt+1(i)，即.

上式中：Bt为归一化因子.

1.3 MEA-AdaBoost-BP算法模型

AdaBoost-BP神经网络模型受限于BP神经网络易过度拟合和泛化能力弱的特点，在工程结构可靠性求解中具有局限性.文中提出MEA-AdaBoost-BP算法模型，运用MEA算法全局搜索最优个体并解码，构造T个BP神经网络弱预测器函数；然后，运用AdaBoost加权组合得到MEA-AdaBoost-BP强预测器函数，最终用强预测器函数代替功能函数求解结构可靠性.MEA-AdaBoost-BP算法模型可靠性求解流程图，如图3所示.MEA-AdaBoost-BP算法模型有如下8个主要步骤.

图3 MEA-AdaBoost-BP算法模型可靠性求解流程图

步骤1在MEA-AdaBoost-BP算法模型中用MEA算法初始化输入集，对子种群SG、初始种群r、优胜子种群m、临时子种群n进行种群编码.即SG=r/(m+n).

步骤2筛选最优个体.为得到得分函数中的最优个体，进行多次迭代和执行趋同、异化操作，最终通过均方误差(SE)计算MEA得分(Val).即Val=1/SE.

步骤3根据编码解码规则.将最优个体依照编码解码得到权值和阈值，并将其赋予BP神经网络构造弱预测器.

步骤4数据初始化.随机选择M组训练数集，运用已优化权值和阈值的BP神经网络构造T个弱预测器，并赋予相同的初始分布权值，即Dt(i)=1/M，i=1，2，…，M；t=1，2，…，T.

步骤6权重预测与调整.若预测误差和et大于设定误差，根据权重Dt(i)计算调整下一个权重Dt+1(i).则有

上式中：Bt为归一化因子.

步骤8功能函数的运用.下式功能函数式Z由强预测函数y(x)代替，进行可靠度指标求解.即有

上式中：ωL为权矩阵；fL为传递函数.

2 MEA-AdaBoost-BP算法验证

2.1 理论模型验证

为验证和优化MEA-AdaBoost-BP模型，考虑乘积形式的非线性结构功能函数Z(H，W)，结构功能函数为Z=g(X)=H·W-1 140=0，H和W相互独立，均服从正态分布，均值为μH=38，μW=54，标准差为σH=3.8，σW=2.7，进行可靠指标β和失效概率Pf求解.采用MEA-AdaBoost-BP算法模型生成精确有效的MEA-AdaBoost-BP强预测器函数，运用MEA-AdaBoost-BP算法模型生成2 000个{xi，g(xi)}数据集.MEA参数设定为种群数r=200，优胜子种群数m=5，和临时子种群数n=5，迭代训练参数设置为20次.BP神经网络参数设置迭代次数为100、学习率为0.1、目标误差为1×10-8.

根据MEA-AdaBoost-BP算法模型设置参数，此时误差性能曲线迭代平滑，迭代次数为16次，网络预测精度为2.377 9×10-5，达到预测精度要求.MEA-AdaBoost-BP算法模型的误差性能曲线，如图4所示.图4中：N为迭代数；εMS为均方误差.

图4 理论模型的误差性能曲线图

多算法计算结果对比，如表1所示.表1中：β为可靠度指标；ε为误差；εa为误差绝对值；Pf为失效概率.从表1可知：AdaBoost-BP预测器误差绝对值较大，可靠性指标计算精度较差，通过MEA-AdaBoost-BP对弱预测器进行优化构成强预测器其误差绝对值仅为0.005 7，可靠性指标β=5.282 7，误差值仅为1.59%，精度有大幅提升.

表1 不同算法的计算结果对比

2.2 桁架工程模型验证

2.2.1 参数设定 选用文献[8-9]中的23杆桁架，桁架结构如图5所示.图5的10个随机变量：横杆和斜杆的横截面积和杨氏模量分别为A1，A2，E1，E2，随机荷载P1～P6.假设所有变量独立，其分布、均值、标准差如表2所示.

图5 桁架结构图

表2 桁架结构的随机参数变量分布

该结构在载荷P1～P6作用下，点C位移最大，参考文献[8]结构功能函数为

Z=G(x)=0.14-|Vc(x)|.

根据多次训练比较，BP神经网络参数设置迭代次数为100、学习率为0.1、目标误差为1×10-8，权值为ω1，ω2，阈值为B1，B2.通过MEA-AdaBoost-BP算法模型将10组弱预测器函数迭代训练组合成一个MEA-AdaBoost-BP强预测器函数.根据设置参数，MEA-AdaBoost-BP算法模型桁架结构的误差性能曲线图，如图6所示.从图6可知：此时误差性能曲线迭代平滑，迭代次数46次，网络预测精度为9.773 1×10-7，达到预测精度要求.

图6 桁架结构的误差曲线图

2.2.2 模型预测结果 AdaBoost-BP算法和MEA-AdaBoost-BP算法的预测误差绝对值对比，如图7所示.图7中：εa为误差绝对值；n为预测样本数.

从图7可知：运用传统的AdaBoost-BP预测器函数进行预测其误差绝对值为0.004 7，预测误差绝对值只有50%左右，在0.05以下，且误差绝对值曲线波动幅度相对较大，从而可知预测效果较差；而运用MEA算法进一步优化AdaBoost-BP预测器函数，由于采用多个AdaBoost-BP弱预测器函数构建MEA-AdaBoost-BP强预测器函数进行预测，其预测误差绝对值为0.002 0，且预测误差绝对值90%，也在0.05以下，但误差绝对值曲线波动幅度较小，具有更好的泛化能力和预测性.

为验证MEA-AdaBoost-BP神经网络算法模型的可行性，将两者的预测误差绝对值进行对比，可知MEA-AdaBoost-BP预测器具有更好的预测效果，能够更好的构造功能函数.

将文献[8]的计算结果和Monte-Carlo法计算结果设置为标准解，证明MEA-AdaBoost-BP算法模型的精确性和可行性.采用Monte-Carlo法、AdaBoost-BP神经网络法、MEA-AdaBoost-BP神经网络算法模型，分别对桁架结构功能函数进行可靠性指标求解分析，可靠度计算指标如表3所示.表3中：β为可靠度指标；ε为误差；εa为误差绝对值；Pf为失效概率.

由表3可知，MEA-AdaBoost-BP算法模型求解可靠性指标值较AdaBoost-BP算法模型求解可靠性指标值更为接近文献[8]和Monte-Carlo法解值，可靠性指标β=3.900，误差仅为1.88%.由此可知，文中所提方法能更好地逼近结构功能函数求解可靠性指标，比传统方法具有更优异的精度性和可行性.

3 结论

基于MEA-AdaBoost-BP神经网络算法模型逼近结构功能函数求解可靠性指标，并通过与不同算法比较验证，得到以下3点主要结论.

1)采用MEA-AdaBoost-BP神经网络算法模型，运用思维进化算法(MEA)赋予BP弱预测器最优初始权值和阈值，并用AdaBoost算法加权组合多个BP弱预测器形成MEA-AdaBoost-BP强预测器.与AdaBoost-BP算法相比，有效提升了BP神经网络的预测精准性.

2)在前人可靠性研究中，对运用BP神经网络构造隐性功能函数求解可靠度指标，提出一种基于MEA-AdaBoost优化BP神经网络权值和阈值的新思路，提高构建隐性功能函数的精确度.

3)通过Monte-Carlo法、AdaBoost-BP神经网络算法、MEA-AdaBoost-BP神经网络算法求解可靠性指标β的比较，可知基于MEA-AdaBoost-BP改进一次二阶矩模型可靠性求解中，可靠度指标β值与Monte-Carlo法解值相近，达到求解精度.同时，文中所提方法仅两次分别迭代16次和46次，与Monte-Carlo法相比减少大量的数值计算次数.