一种适用于车载自组网的无证书签名方案
2022-05-10殷新春
朱 栋,殷新春,2
1(扬州大学 信息工程学院,江苏 扬州 225127)
2(扬州大学 广陵学院,江苏 扬州 225128)
1 引 言
随着私家车辆数量的不断增多,许多国家地区的运输系统正日益趋于极限,GROSS[1]预计,到2035年全球使用的车辆数目将达到20亿.汽车保有量的持续增长,一方面给人们的生活带来了很多的便利,另一方面造成了城市交通拥堵、交通事故频发等问题.因此,保障驾驶安全的需求越来越紧迫.正是在这种背景下,车载自组网(Vehicular Ad-Hoc Networks,VANETs)应运而生.车载自组织网络被归类为移动自组织网络(Mobile Ad-Hoc Network,MANET)的一种应用,具有改善道路安全性和为旅行者提供舒适感的潜力.车辆通过蜂窝网-车到万物(Cellular Vehicle to Everything,C-V2X)[2]的通信技术与路边基础设施进行通信进而获得实时的路况、天气等信息.同时,车辆行驶的交通状态信息(速度、路况、行驶路线)也需要实时的被路边基础设施收集和处理,借助无线通信网络和可信中心(Trusted Authority,TA)的信息处理能力分析城市的交通流量、拥堵情况,从而对车辆进行路径规划,实现智能化的交通管理,这样才能实现交通信息的最大化利用.
由于车辆与基础设施(Vehicle to Infrastructure,V2I)之间采用无线通信的方式,数据在传送过程中极易被监控、篡改或伪造[3].面向车载自组网的安全通信方案需要通过签名技术保证通信的基本安全需求,例如消息的认证性、完整性和不可否认性.安全通信方案还需要提供条件隐私保护机制.一方面车辆用户的隐私信息(真实身份标识、位置等)一旦泄露会导致被追踪的风险增加.另一方面当车辆用户发送虚假消息或者肇事逃逸时,可信中心必须能够追查到车辆用户的真实身份.最后,安全通信方案还需要较高的计算效率.随着联网车辆数量的不断增加,路边基础设施需要面对海量的待验证消息,较低的计算效率会导致路边基础设施无法及时完成这些消息的验证;面向VANETs的交通安全相关的消息具有很强的时效性,必须被及时有效地处理,否则可能因处理延误造成交通事故[4].综上所述,在满足通信安全需求的基础上提高方案的匿名认证效率是车载自组网要解决的关键问题.
最近,Thumbur等人[5]提出了一种无双线性配对的无证书签名方案,并在随机预言模型下对其安全性进行了证明,声称该方案可以部署在资源受限的车载自组网中.但是,我们发现该方案并不能抵抗公钥替换攻击,即不具备其所声称的安全性.为了解决上述问题,本文提出了一种可证明安全且匿名的无证书签名方案.该方案满足车载自组网的安全需求,同时具有较低的计算和通信开销.本文的主要贡献如下:
1)分析了Thumbur等人[5]的方案,证明该方案无法抵抗公钥替换攻击,并给出了具体的攻击方法.
2)提出了一种适用于车载自组网的无证书签名方案.本文方案不需要安全信道并且能够满足基本安全需求.
3)在随机预言模型下证明了本文方案基于椭圆曲线离散对数问题具有不可伪造性.
4)性能分析表明,与其他应用于车载自组网的方案相比,本文方案在计算与通信性能上都有优势.
2 相关工作
传统公钥密码体系使用数字证书确认用户公钥的有效性[6],而数字证书由证书管理机构(Certificate Authority,CA)颁发和维护.一些应用于车载自组网的签名方案[7,8]是建立在传统的公钥密码体系上的.尽管基于该体系的签名方案提供了对消息的完整性和认证性的验证,但是,在车载自组网中,每个实体都在高流量、高密度的情况下交互信息,数字证书的管理无疑大大增加了其中的存储和通信负担.为了简化证书管理,Shamir等人[9]提出了基于身份的公钥密码体系.后来,文献[10-13]将基于身份的公钥密码体系引入到车载自组网中,设计了基于身份的公钥密码体系认证方案.在基于身份的公钥密码体系中,公钥是由签名者的公共身份信息(电话号码、电子邮件和身份证号码等)生成的,因而不需要可信机构颁发数字证书认证公钥的有效性.但用户的私钥由第3方私钥生成中心(Private Key Generator,PKG)生成,若第3方私钥生成中心是不诚实或恶意的,其可以伪造任意用户的签名,即存在密钥托管问题.
为了解决密钥托管问题,Al-Riyami等人[14]提出了无证书公钥密码体系.在无证书公钥密码体系中,签名者的私钥由密钥生成中心(Key Generation Center,KGC)生成的部分私钥和签名者选取的秘密值构成.由于KGC无法得知签名者的秘密值,也就无法得知签名者的完整私钥.另外,签名者的公钥是由他自己选取的秘密值计算而来的,所以无需数字证书.因此,无证书密码体系解决了密钥托管问题并且避免了证书管理.Horng等人[15]提出了一种适用于车载自组网的具有条件隐私保护功能的无证书聚合签名方案,并声称该方案在自适应选择消息攻击下具有不可伪造性.但是,Li等人[16]指出Horng等人[15]的方案不能抵抗恶意KGC的攻击.文献[17]提出了一种基于双线性配对的无证书聚合签名方案,并在随机预言模型下证明该方案是安全的.然而,文献[18]指出文献[17]的方案无法抵抗恶意KGC的攻击.Wang等人[19]设计了一种基于双线性配对的无证书聚合签名方案,并声称该方案满足不可伪造性和匿名性.但是,文献[20]指出文献[19]的方案不能抵抗恶意KGC的攻击、无法实现车辆的隐私保护且车辆真实身份的追踪需要花费较大的计算开销和存储空间.在2020年,Mei等人[21]提出了一种基于双线性配对的具有条件隐私保护功能的无证书聚合签名方案,该方案实现了完全聚合并在随机预言模型下被证明是安全的.
上述方案[15-19,21]都是基于双线性配对构造的,由于双线性配对的计算开销较大,会加大路边单元(Road Side Unit,RSU)验证签名的计算开销.为了提高计算效率,Gayathri等人[22]提出了一种无双线性配对的无证书批量认证方案,并在随机预言模型下证明了该方案的安全性.在该方案中,车辆需要向周边的RSU发送身份信息请求为其生成假名,若攻击者通过沿途广播RSU的消息诱使车辆请求假名可能会导致车辆的位置遭到泄露,而方案[19,20]存在同样的问题.文献[23]提出了一种无双线性配对的无证书聚合签名方案,声称该方案实现了条件隐私保护,并在随机预言模型下给出了安全性证明.但是,文献[24]指出文献[23]的方案无法抵抗恶意KGC的攻击.
最近,Thumbur等人[5]提出了一种无双线性配对的无证书签名方案,声称该方案在随机预言模型下基于椭圆曲线离散对数问题具有不可伪造性.但是我们发现该方案无法抵抗公钥替换攻击,所以是不安全的方案.因此,设计适用于车载自组网的安全且高效的无证书签名方案是本文的主要目标.
3 预备知识
首先,本节描述了适用于本文方案的困难性问题.然后,描述了车载自组网的系统模型和安全需求.最后,给出无证书签名方案的定义和安全模型.本文方案的部分符号及说明如表1所示.

表1 本文方案的部分符号及说明Table 1 Symbols used in our scheme
3.1 困难性问题
椭圆曲线离散对数问题(Elliptic Curve Discrete Logarithm Problem,ECDLP):取阶为大素数q的群G,P为群G的任意一个生成元.已知P和aP∈G,ECDLP的目标是计算a∈Zq*.
计算性Diffie-Hellman问题(Computational Diffie-Hellman Problem,CDHP):取阶为大素数q的群G,P为群G的任意一个生成元.已知P和aP∈G,bP∈G,对于任意未知的a,b∈Zq*,CDHP的目标是计算abP∈G.
3.2 车载自组网的系统模型
如图1所示,车载自组网的系统模型包括3个参与者:可信中心(TA),车载单元(On Board Unit,OBU),路边单元(RSU).
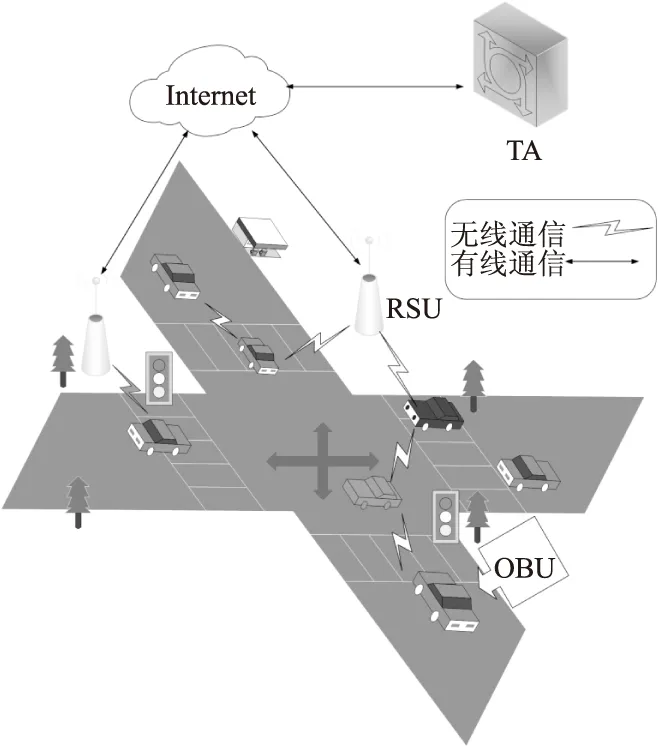
图1 车载自组网的系统模型示例图Fig.1 System model for VANETs
1)TA:通常为交通管理部门.一般来说,TA被认为是完全可信的实体,拥有强大的通信、计算和存储能力.但是,基于零信任架构[25]的思想,我们假设TA是不完全可信的.TA通过有线信道与RSU通信,主要负责车载自组网的系统建立以及为各个OBU生成部分私钥.由于事先存储了车辆的真实身份列表,TA可以根据恶意车辆的假身份恢复出真实身份.
2)OBU:车辆装载的通信模块.车辆通过OBU能够与RSU或其他配备OBU的车辆进行通信,进而获得相应的服务.同时,OBU可以生成假名、公钥和消息的签名.
3)RSU:安装在道路两侧的基础设施.RSU通过无线信道向范围内的车辆广播自己的身份和公钥,验证OBU发送的消息签名对.然后,它会将有效的消息处理或收集起来发送给TA,并将从TA处接收的信息以广播的形式传递给周围的OBU.若RSU周边出现事故,RSU有权向TA举报并协助TA追踪恶意车辆.
3.3 安全需求
1)认证性和完整性:RSU要确保所接收的消息是来自注册过的车辆,即消息来源是可靠且未被篡改的.
2)匿名性:车载自组网的其他车辆或攻击者无法通过车辆的假名识别出车辆的真实身份.
3)可追踪性:当某个OBU发送虚假消息或者肇事逃逸时,相应的RSU能够协助TA追踪违规车辆的真实身份,车辆无法利用匿名性逃脱惩罚.
3.4 无证书签名方案的定义
本小节结合车载自组网的系统模型,给出了本文定义的无证书签名方案的主要算法.无证书签名方案由8个多项式时间算法构成,具体的算法如下所述:
1)系统建立算法(Setup):该算法由TA执行.输入安全参数k,输出系统参数params和系统主密钥s.TA公开params并秘密保存s.
2)车辆注册算法(VehicleRegistration):该算法由OBU执行.输入params、车辆i的真实身份RIDi,输出该车辆的假身份Qi和协商密钥Zi.OBU通过周边的RSU将(Qi,Zi)发送给TA.
3)提取部分私钥算法(ExtractPPK):该算法由TA执行.输入params、s、Qi和Zi,输出车辆i的部分私钥的转换值ki以及部分公钥Ri.TA通过RSU将(ki,Ri)发送给相应的OBU.
4)设置秘密值算法(SetSecretValue):该算法由OBU执行.输入params,输出车辆i的秘密值xi.
5)设置公/私钥算法(SetPublic/PrivateKey):该算法由OBU执行.输入params、ki和xi,输出车辆i的公钥PKi和私钥SKi.
6)假名生成算法(PseudonymGen):该算法由OBU执行.输入params、xi、Qi、OBU的当前时间戳Ti、车辆周边RSU的身份Pj和公钥Yj,输出车辆i的假名IDi.
7)签名算法(Sign):该算法由OBU执行.输入params、IDi、SKi和消息m,输出签名σi.OBU将请求消息Req=(IDi,m,σi,PKi)发送给周边的RSU.
8)验证算法(Verify):该算法由RSU执行.输入params、IDi、PKi、m和σi,RSU验证σi是否有效,若签名有效,输出VALID;否则,输出INVALID.
3.5 无证书签名的安全模型
在Huang等人[26]的安全模型中有两类攻击者:类型I攻击者AⅠ,类型II攻击者AⅡ.AⅠ为恶意的车载单元,可以替换合法车辆的公钥,但是无法获取系统主密钥;AⅡ为恶意但被动的TA,可以自己生成系统参数,但是不能替换车辆的公钥.下面分别在游戏Ⅰ和游戏Ⅱ中刻画这两类的攻击者.
游戏Ⅰ.该游戏是由挑战者CⅠ和攻击者AⅠ进行如下交互完成的,CⅠ维护用户列表Luser.
阶段1.输入安全参数k,CⅠ运行系统建立算法生成系统参数params和系统主密钥s.CⅠ发送params给AⅠ,并秘密保存s.
阶段2.在该阶段,AⅠ向CⅠ进行以下询问:
1)创建用户询问:该询问会产生车辆IDi生成签名所需要的所有参数.AⅠ选择一个身份IDi提交给CⅠ,CⅠ查询列表Luser,检验该用户是否已被创建.若已创建,则CⅠ返回公钥PKi给AⅠ;否则,CⅠ运行提取部分私钥算法,设置秘密值算法,设置公/私钥算法,从而获得(di,xi,PKi).然后,CⅠ返回公钥PKi给AⅠ并将(IDi,di,xi,PKi,flag)加入列表Luser,其中flag默认为False.
2)替换公钥询问:AⅠ选择一个身份IDi和(x′i,PK′i)提交给CⅠ,当接收到AⅠ提交的替换公钥询问时,CⅠ从列表Luser中获取(IDi,di,xi,PKi,flag),用(x′i,PK′i)替换列表Luser中的(xi,PKi),CⅠ会记录这一替换并令flag=True.
3)秘密值询问:AⅠ选择一个身份IDi提交给CⅠ,当接收到AⅠ提交的秘密值询问时,CⅠ从列表Luser中获取(IDi,di,xi,PKi,flag)并返回Luser中的xi给AⅠ.如果flag=True,返回的xi为⊥.
4)部分私钥询问:AⅠ选择一个身份IDi提交给CⅠ,当接收到AⅠ提交的部分私钥询问时,C1从列表Luser中获取(IDi,di,xi,PKi,flag)并返回Luser中的di给AⅠ.
5)签名询问:AⅠ选择一个身份IDi和消息m提交给CⅠ,当接收到AⅠ提交的签名询问时,CⅠ运行签名算法生成消息m的签名σi,并把σi返回给AⅠ.这里的σi满足VALID←Verify(params,m,σi,PK′i,IDi),其中,PK′i是目前的公钥,这个公钥可以是AⅠ替换后的公钥.
阶段3.该阶段是伪造阶段,AⅠ输出(IDi*,m*,σi*),IDi*是AⅠ选择伪造签名的目标用户,m*是伪造消息,σi*是关于(IDi*,m*)的伪造签名.若同时满足下面的条件,我们称AⅠ赢得了这个游戏.
1)VALID←Verify(params,m*,σi*,PKi*,IDi*);
2)AⅠ不能提交关于目标用户IDi*对m*的签名询问;
3)AⅠ不能提交关于目标用户IDi*的部分私钥询问.
游戏Ⅱ.该游戏是由挑战者CⅡ和攻击者AⅡ进行如下交互完成的.
阶段1. 输入安全参数k,AⅡ运行系统建立算法生成系统参数params和系统主密钥s.AⅡ发送params和s给CⅡ.
阶段2. 在该阶段,AⅡ自适应性的向CⅡ提交创建用户询问,部分私钥询问,签名询问,步骤与游戏Ⅰ的询问一致.
阶段3. 该阶段是输出阶段,AⅡ输出(IDi*,m*,σi*),IDi*是AⅡ选择伪造签名的目标用户,m*是伪造消息,σi*是关于(IDi*,m*)的伪造签名.若同时满足下面的条件,我们称AⅡ赢得了这个游戏.
1)VALID←Verify(params,m*,σi*,PKi*,IDi*);
2)AⅡ不能提交关于目标用户IDi*对m*的签名询问.
4 Thumbur等人方案的安全性分析
在本节中,我们简单回顾Thumbur等人[5]的无证书签名方案,并分析该方案存在的安全性问题.
4.1 方案的回顾[5]

2)提取部分私钥算法(ExtractPPK):输入params、签名者的身份IDi,KGC随机选取ri∈Zq*,计算部分公钥Ri=riP,h1=H1(IDi‖Ri‖Ppub),部分私钥di=(ri+sh1)modq.KGC通过安全信道将Di=(di,Ri)发送给签名者.签名者验证等式diP=Ri+h1Ppub是否成立,若成立则接受,否则拒绝.
3)设置秘密值算法(SetSecretValue):签名者随机选取xi∈Zq*作为秘密值.
4)设置公/私钥算法(SetPublic/PrivateKey):输入params、IDi、xi和di,签名者计算Xi=xiP,h2=H2(IDi‖Xi),部分公钥Qi=Ri+h2Xi.然后,签名者设置公钥PKi=(Qi,Ri),设置私钥SKi=(di,xi).
5)签名算法(Sign):输入params、待签名的消息m、SKi和PKi,签名者随机选取ui∈Zq*,计算Ui=uiP,h2=H2(IDi‖Xi),h3=H3(IDi‖m‖PKi‖Ui),vi=ui+h3(di+h2xi)modq.然后,签名者设置签名σi=(Ui,vi),并发送σi给验证者.
6)验证算法(Verify):输入params、IDi、m、PKi和σi,验证者计算h1=H1(IDi‖Ri‖Ppub),h3=H3(IDi‖m‖PKi‖Ui),验证等式viP=Ui+h3(Qi+h1Ppub)是否成立.若成立,输出VALID;否则,输出INVALID.
4.2 公钥替换攻击
伪造攻击方法:正常情况下,类型I攻击者伪造有效的签名需要计算出部分私钥,而部分私钥是由主密钥s计算而来的.虽然攻击者可以窃听到系统公钥,但是攻击者试图从系统公钥进一步计算出s可归约为椭圆曲线离散对数问题.因此,攻击者无法计算出部分私钥,也就无法伪造签名.另一种办法就是消除部分私钥的影响,寻找线性式[27](公钥或部分公钥与系统公钥的简单线性组合),利用替换公钥的方法消除主密钥对应的系统公钥,伪造签名就不再需要合法用户持有的部分私钥了.
验证等式中存在线性式Qi+h1Ppub,因此类型I攻击者可以利用替换公钥的能力消除h1Ppub,其中Ppub=sP.攻击者将执行以下操作.
伪造:恶意的用户攻击步骤如下.
1)随机选取x′i,r′i∈Zq*,计算X′i=x′iP,R′i=r′iP,h1=H1(IDi‖R′i‖Ppub),h2=H2(IDi‖X′i),Q′i=R′i+h2X′i-h1Ppub;
2)替换公钥为PK′i=(Q′i,R′i);
3)随机选取u′i∈Zq*,计算U′i=u′iP;
4)选择一个消息m*≠m,计算h3=H3(IDi‖m*‖PK′i‖U′i),v′i=u′i+h3(r′i+h2x′i)modq;
5)设置签名σ′i=(U′i,v′i);
6)通过安全信道将
验证:验证者接收到
1)计算h1=H1(IDi‖R′i‖Ppub),h3=H3(IDi‖m*‖PK′i‖U′i);
2)验证等式v′iP=U′i+h3(Q′i+h1Ppub)是否成立,若成立,输出VALID;否则,输出INVALID.
正确性:伪造签名的正确性由下式保证.
v′iP=[u′i+h3(r′i+h2x′i)]P
=U′i+h3(R′i+h2X′i-h1Ppub+h1Ppub)
=U′i+h3(Q′i+h1Ppub).
5 本文方案及正确性分析
5.1 本文方案
为了抵抗文献[5]存在的公钥替换攻击,同时实现车辆身份的条件隐私保护,本文提出了一种适用于车载自组网的无安全信道的无证书签名方案,主要计算和信息传输如图2所示.假设:TA已经保存了系统内所有车辆的真实身份,并将其存储至车辆身份列表;每个RSU设定身份为Pj,随机选取yj∈Zq*作为其私钥,计算公钥Yj=yjP并将(Pj,Yj)发送给TA.

图2 本文方案的流程图Fig.2 Flow chart of the proposed scheme
1)系统建立算法(Setup):该算法由TA执行.输入安全参数k,TA运行该算法生成q阶加法循环群G,P为群G的生成元.TA随机选取并保存s∈Zq*为系统主密钥,计算系统公钥Ppub=sP,选取安全的Hash函数H:G→{0,1}*,H′:G×{0,1}*→Zq*,H1:{0,1}*→Zq*,H2:{0,1}*×{0,1}*×G×G→Zq*,H3:{0,1}*×{0,1}*×G×G→Zq*,并审核RSU发送的(Pj,Yj),审核通过则接收.最后,TA输出系统公共参数params={q,G,P,Ppub,H1,H2,H3,H,H′,(Pj,Yj)}.
2)车辆注册算法(VehicleRegistration):该算法由OBU执行.OBU随机选取zi∈Zq*,计算协商密钥Zi=ziP,假身份Qi=RIDi⊕H(ziPpub),并通过周边的RSU将(Zi,Qi)发送给TA.
4)设置秘密值算法(SetSecretValue):该算法由OBU执行.OBU接收到ki后,计算部分私钥di=ki+H(ziPpub)modq,h1=H1(Qi‖Ri‖Ppub),验证等式diP=h1Ppub+Ri是否成立.若等式不成立,则重新请求部分私钥;若等式成立,则接收,OBU随机选取xi∈Zq*作为秘密值,计算Xi=xiP.
5)设置公私/钥算法(SetPublic/PrivateKey):该算法由OBU执行.OBU设置公钥PKi=(Xi,Ri),设置私钥SKi=(di,xi).
6)假名生成算法(PseudonymGen):该算法由OBU执行.当车辆进入RSU负责的区域内会接收到RSU广播的身份和公钥信息,若OBU根据系统参数检查出RSU的身份与公钥信息不匹配,则不执行该算法;否则,OBU获取当前的时间戳Ti以及RSU的公钥Yj,计算IDi1=Qi⊕H′(xiYj‖Ti),IDi2=Pj(Pj为RSU的身份),设置车辆的假名IDi=(IDi1,IDi2,Ti).
7)签名算法(Sign):该算法由OBU执行.OBU随机选取ui∈Zq*,计算Ui=uiP,h2=H2(IDi‖m‖PKi‖Ui),h3=H3(IDi‖m‖Ppub‖Ui),vi=ui+h2xi+h3dimodq,OBU生成签名σi=(Ui,vi).OBU将请求消息Req=(σi,m,IDi,PKi)发送给RSU.
5.2 正确性分析
正确性分析:本文方案的正确性由以下方程式保证.
viP=(ui+h2xi+h3di)P
=Ui+h2Xi+h3(ri+sh1)P
=Ui+h2Xi+h3(Ri+h1Ppub).
6 安全性分析
6.1 可证明安全
定理1. 在随机预言模型中,若存在一个类型I攻击者AⅠ能在概率多项式时间内以ε的优势成功伪造一个签名,那么存在一个挑战者CⅠ能够在概率多项式时间内以ε1的优势解决椭圆曲线离散对数问题.
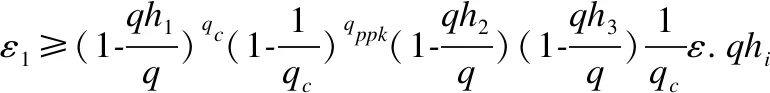
证明:假设CⅠ是一个椭圆曲线离散对数问题的解决者,困难问题的输入(G,P,Ppub=sP),其中s∈Zq*,CⅠ的目标是计算s.
C1维护列表L1,L2,L3,Luser分别用于跟踪AⅠ对预言机H1,H2,H3的Hash询问以及创建用户询问.初始时各列表均为空,AⅠ和CⅠ之间的交互如下.
阶段1.C1运行系统建立算法,将系统参数params={q,G,P,Q,H1,H2,H3,H,H′,(Pj,Yj)}发送给AⅠ.然后,AⅠ挑选车辆IDi*作为目标用户.
阶段2.AⅠ适应性地向CⅠ提交最多多项式有界次的询问如下:
1)H1询问:当CⅠ收到AⅠ的H1(Qi‖Ri‖Ppub)询问时,若列表L1中包含(Qi,Ri,Ppub,h1),则CⅠ返回h1给AⅠ;否则,CⅠ随机选取h1∈Zq*,将(Qi,Ri,Ppub,h1)加入列表L1,并返回h1给AⅠ.
2)H2询问:当CⅠ收到AⅠ的H2(IDi‖m‖PKi‖Ui)询问时,若列表L2中包含(IDi,m,PKi,Ui,h2),则CⅠ返回h2给AⅠ;否则,CⅠ随机选取h2∈Zq*,将(IDi,m,PKi,Ui,h2)加入列表L2,并返回h2给AⅠ.
3)H3询问:当CⅠ收到AⅠ的H3(IDi‖m‖Ppub‖Ui)询问时,若列表L3中包含(IDi,m,Ppub,Ui,h3),则CⅠ返回h3给AⅠ;否则,CⅠ随机选取h3∈Zq*,将(IDi,m,Ppub,Ui,h3)加入列表L3,并返回h3给AⅠ.
4)创建用户询问:当CⅠ收到AⅠ的创建用户询问时,CⅠ查询列表Luser,若列表Luser中包含(IDi,di,xi,Xi,Ri,flag),则CⅠ返回PKi=(Xi,Ri)给AⅠ;否则,CⅠ执行以下操作:①如果IDi≠IDi*,CⅠ随机选取di,h1,xi∈Zq*,计算Xi=xiP,Ri=diP-h1Ppub,令flag=Flase.②如果IDi=IDi*,CⅠ随机选取h1,ri,xi∈Zq*,计算Xi=xiP,Ri=riP,令di=⊥,flag=Flase.最后,CⅠ检查列表L1,若列表L1中包含(Qi,Ri,Ppub,H1(Qi,Ri,Ppub))且h1≠H1(Qi,Ri,Ppub),则CⅠ终止程序;否则,CⅠ返回PKi=(Xi,Ri)给AⅠ,将(IDi,di,xi,Xi,Ri,flag),(Qi,Ri,Ppub,h1)分别加入列表Luser,L1.
5)替换公钥询问:当AⅠ想用新公钥PK′i替换IDi的旧公钥PKi时,我们这里假设AⅠ已经提交过关于IDi的创建用户询问,CⅠ从列表Luser中获取(IDi,di,xi,Xi,Ri,flag),更新列表中的(xi,Xi,Ri)为(x′i,X′i,R′i)并令flag=True.
6)秘密值询问:当CⅠ收到AⅠ的秘密值询问时,CⅠ检查列表Luser,若列表Luser中包含(IDi,di,xi,Xi,Ri,flag),CⅠ返回xi给AⅠ;否则,CⅠ先提交关于IDi的创建用户询问再返回xi给AⅠ.如果flag=True,返回的xi为⊥.
7)部分私钥询问:当CⅠ收到AⅠ的部分私钥询问时,我们这里假设AⅠ已经提交过关于IDi的创建用户询问,CⅠ执行以下操作:当IDi=IDi*时,CⅠ终止程序;当IDi≠IDi*时,CⅠ查询列表Luser,返回di给AⅠ.
8)签名询问:当AⅠ对(IDi,m)提交签名询问时,CⅠ查询列表Luser和L1,当IDi≠IDi*时,CⅠ从Luser,L1中获取(IDi,di,xi,Xi,Ri,flag),(Qi,Ri,Ppub,h1),这种情况下di,xi不为⊥,CⅠ随机选取ui,h2,h3∈Zq*,计算Ui=uiP,vi=(ui+h3di+h2xi)modq,其中H2(IDi‖m‖PKi‖Ui)=h2,H3(IDi‖m‖Ppub‖Ui)=h3,CⅠ返回签名σi=(Ui,vi)给AⅠ,将(IDi,m,PKi,Ui,h2),(IDi,m,Ppub,Ui,h3)分别加入列表L2,L3.当IDi=IDi*时,CⅠ从Luser,L1获取(IDi,di,xi,Xi,Ri,flag),(Qi,Ri,Ppub,h1),其中di=⊥,xi=⊥(AⅠ提交过替换公钥询问并且没有提供与之对应的xi).CⅠ随机选取vi,h2,h3∈Zq*,计算Ui=viP-h3(Ri+h1Ppub)-h2Xi,CⅠ返回签名σi=(Ui,vi)给AⅠ,将(IDi,m,PKi,Ui,h2),(IDi,m*,Ppub,Ui,h3)分别加入列表L2,L3.
阶段3.AⅠ停止上述询问,输出关于(IDi*,m*)的伪造签名σi*=(Ui*,vi*).当IDi*≠IDi时,CⅠ终止游戏;否则,CⅠ查询列表Luser,L1,L2,L3并从中获取出(IDi*,di*,xi*,Xi*,Ri*),(Qi*,Ri*,Ppub,h1*),(IDi*,m*,PKi*,Ui*,h2*),(IDi*,m*,Ppub,Ui*,h3*),如果h2*,h3*不在列表L2,L3中,CⅠ终止游戏.
vi*=ui*+h3*di*+h2*xi*modq
(1)
由于di*=sh1*+ri*,其中h1*=h1,ri*=ri,所以式(1)可以改写为:
vi*=ui*+h3*(ri+sh1)+h2*xi*modq
(2)
要注意的是xi*不一定是起初CⅠ挑选的xi,因为AⅠ有可能提交过关于IDi的替换公钥询问,所以对于CⅠ来说ui*,s,ri,xi*都是未知的,根据分叉引理[28],AⅠ会获得关于消息m*的另外3个有效的签名:
通过解4个线性无关方程,CⅠ会计算出s作为椭圆曲线离散对数问题的有效解,从而解决椭圆曲线离散对数问题.
接下来,我们评估CⅠ解决椭圆曲线离散对数问题的优势.
事件1(E1):表示CⅠ没有终止过游戏Ⅰ.
事件2(E2):vi*是一个关于(IDi*,m*)的有效签名.
CⅠ解决椭圆曲线离散对数问题的优势为:ε1=Pr[E1∧E2]=Pr[E1]Pr[E2/E1],其中,Pr[E2/E1]=ε.依据游戏分析,可以得到:




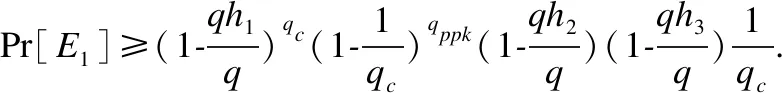
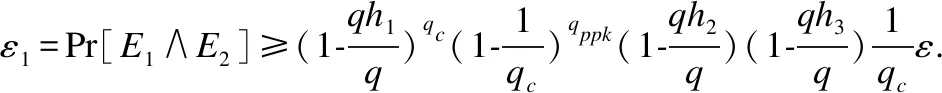
显然,若AⅠ具有成功伪造一个签名的优势ε,那么CⅠ就具有解决椭圆曲线离散对数问题的能力,但这与椭圆曲线离散对数问题无法解决矛盾,即可证明攻击者AⅠ成功伪造一个签名的优势可忽略.所以,本文方案能够抵抗类型I攻击者.
定理2. 在随机预言模型中,若存在一个类型II攻击者AⅡ能在概率多项式时间内以ε′的优势在游戏Ⅱ中获胜,那么存在一个挑战者CⅡ能够在概率多项式时间内以ε2的优势解决椭圆曲线离散对数问题.

证明:假设CⅡ是一个椭圆曲线离散对数问题的解决者,其困难问题的输入(G,P,Q=xP),其中x∈Zq*,CⅡ的目标是计算x.
CⅡ维护列表L1,L2,L3,Luser分别用于跟踪AⅡ对预言机H1,H2,H3的Hash询问和创建用户询问.初始时各列表均为空,AⅡ和CⅡ之间的交互如下.
阶段1.AⅡ运行系统建立算法,并将系统参数params={q,G,P,Ppub,H1,H2,H3,H,H′,(Pj,Yj)}和系统主密钥s发送给CⅡ.AⅡ挑选车辆IDi*作为目标用户.
阶段2.AⅡ适应性地向CⅡ提交最多多项式有界次的询问如下:
1)Hash询问:AⅡ适应性地向CⅡ提交Hash询问,步骤与定理1证明中的Hash询问一致.
2)创建用户询问:当CⅡ收到AⅡ的创建用户询问时,CⅡ查询列表Luser,如果该列表包含对应的公钥,则返回PKi=(Xi,Ri)给AⅡ;否则,CⅡ执行以下操作:①如果IDi≠IDi*,CⅡ随机选取ri,h1,xi∈Zq*,计算Ri=riP,di=sh1+rimodq,Xi=xiP,令flag=False.②如果IDi=IDi*时,CⅡ随机选取ri,h1∈Zq*,计算Ri=riP,di=sh1+rimodq,令flag=False,Xi=Q,xi=⊥.最后,CⅡ查询列表L1,若列表L1中包含(Qi,Ri,Ppub,H1(Qi,Ri,Ppub))并且h1≠H1(Qi‖Ri‖Ppub),则CⅡ终止程序;否则,CⅡ返回PKi=(Xi,Ri)给AⅡ,将(IDi,di,xi,Xi,Ri,flag),(Qi,Ri,Ppub,h1)加入列表Luser,L1.
3)替换公钥询问:当AⅡ想用新公钥PK′i替换IDi的旧公钥PKi时,CⅡ验证AⅡ提交的身份,若IDi=IDi*,则CⅡ拒绝回应AⅡ并终止游戏;否则,CⅡ从列表Luser中获取(IDi,di,xi,Xi,Ri,flag),更新列表中的(xi,Xi,Ri)为(x′i,X′i,R′i)并令flag=True.
4)秘密值询问:当CⅡ收到AⅡ的秘密值询问时,CⅡ验证AⅡ提交的身份,若IDi=IDi*,则CⅡ拒绝回应AⅡ并终止游戏;否则,CⅡ查询列表Luser,返回xi给AⅡ.如果flag=True,返回的xi为⊥.
5)部分私钥询问:我们假设CⅡ收到AⅡ的部分私钥询问时,AⅡ已经提交了创建用户询问,CⅡ查询列表Luser,从中获取(IDi,di,xi,Xi,Ri)并返回di给AⅡ.
6)签名询问:当AⅡ对(IDi,m)提交签名询问时,CⅡ查询列表Luser和L1,当IDi≠IDi*时,CⅡ从Luser,L1获取(IDi,di,xi,Xi,Ri,flag),(Qi,Ri,Ppub,h1),其中xi不为⊥,CⅡ随机选取ui,h2,h3∈Zq*,计算Ui=uiP,vi=(ui+h3di+h2xi)modq,其中H2(IDi‖m‖PKi‖Ui)=h2,H3(IDi‖m‖Ppub‖Ui)=h3,CⅡ返回签名σi=(Ui,vi)给AⅡ,将(IDi,m,PKi,Ui),(IDi,m,Ppub,Ui)分别加入列表L2,L3.当IDi=IDi*时,CⅡ从Luser,L1中获取(IDi,di,xi,Xi,Ri,flag),(Qi,Ri,Ppub,h1),其中xi=⊥.CⅡ随机选取vi,h2,h3∈Zq*,计算Ui=viP-h3(Ri+h1Ppub)-h2Q,CⅡ返回签名σi=(Ui,vi)给AⅡ,将(IDi,m,PKi,Ui,h2),(IDi,m,Ppub,Ui,h3)分别加入列表L2,L3.
阶段3.AⅡ停止上述询问,输出关于(IDi*,m*)的伪造签名σi*=(Ui*,vi*).当IDi*≠IDi时,CⅡ终止游戏;否则,CⅡ查询列表Luser,L1,L2,L3并从中获取(IDi*,di*,xi*,Xi*,Ri*),(Qi*,Ri*,Ppub,h1*),(IDi*,m*,PKi*,Ui*,h2*),(IDi*,m*,Ppub,Ui*,h3*),如果h2*,h3*不在列表L2,L3中,CⅡ终止游戏.
vi*=ui*+h3*di*+h2*xmodq
(3)
由于di*=di,所以式(3)可以改写为:
vi*=ui*+h3*di+h2*xmodq
(4)

(5)
根据式(4)和式(5),CⅡ可计算出x作为椭圆曲线离散对数问题的有效解,从而解决椭圆曲线离散对数问题.
接下来,我们评估CⅡ解决椭圆曲线离散对数问题的优势.
事件1(E1):CⅡ没有终止过游戏Ⅱ.
事件2(E2):vi*是一个关于消息(IDi*,m*)的有效签名.
CⅡ解决椭圆曲线离散对数问题的优势为:ε2=Pr[E1∧E2]=Pr[E1]Pr [E2/E1],其中,Pr [E2/E1]=ε′.依据游戏分析,可以得到:

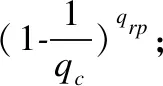
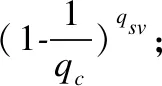




显然,若AⅡ具有成功伪造一个签名的优势ε′,那么CⅡ就具有解决椭圆曲线离散对数问题的能力,但这与椭圆曲线离散对数问题无法解决相矛盾,即可证明攻击者AⅡ成功伪造一个签名的优势可忽略.所以,本文方案能够抵抗类型II攻击者.
6.2 安全需求分析
6.2.1 认证性和完整性
认证性和完整性的证明可以从定理1和定理2证明中获得,即不存在类型I和类型II攻击者能够成功伪造一个签名,只有合法车载单元发送的签名可以通过验证等式.因此,本文方案满足消息的认证性与完整性.
6.2.2 匿名性
匿名性是指OBU在通信过程中,除了OBU本身和TA,其他实体都无法得知车辆的真实身份.车辆的匿名性主要体现在以下两个方面.
1)车辆的假名IDi由OBU计算.车辆的秘密值和RSU的公钥作为输入参数(xiYj=yjXi),其中xi、yj分别为车辆、RSU所私有,基于CDHP,攻击者无法计算出xiyjP.由于TA公布了合法RSU的信息,即使攻击者伪装成RSU也只能广播正确的身份Pj及对应的公钥Yj(Yj=yjP),基于ECDLP,攻击者无法计算出yj,也无法得到车辆实质性的身份信息.这样很好的保证了车辆身份的匿名性.
6.2.3 可追踪性
7 性能分析
本节将从计算开销,通信开销和安全性3个方面对本文方案进行性能分析,并将本文方案与现有的相关方案[5,13,15,19,21,22]进行比较.计算开销主要取决于签名和验证算法的计算量,通过统计椭圆曲线标量乘运算,椭圆曲线标量加运算,双线性配对运算,Hash映射到点运算的执行次数来衡量.对于通信开销,我们根据车辆的签名、假名、当前时间戳和公钥的长度来评估.在安全性方面,我们主要检查方案是否保证消息具有认证性,方案是否提供条件隐私保护以及能否抵挡类型I、类型II的攻击者.
在计算开销方面,我们采用文献[12]中的实验统计结果,各种基础操作的计算开销如表2所示.

表2 基础操作的计算开销Table 2 Computational overhead of operations
由于文献[13,15,19,21]涉及到双线性配对和Hash映射到点运算,而文献[22]中签名和验证算法的点乘运算次数较多,导致上述方案的计算效率较低.如表3所示,相比于其他方案[13,15,19,21,22],本文方案的总开销分别减少了81.3%、87.5%、91.0%、93.8%和28.5%.本文方案的签名开销和验证开销都具有优势.

表3 计算开销的比较Table 3 Comparison of computational cost


表4 通信开销的比较Table 4 Comparison of transmission overhead
如表4所示,在文献[13]的方案中,请求消息由(AIDi,Mi,Si,Ti)组成,签名Si∈G1,假名AIDi=(AIDi,1,AIDi,2),其中AIDi,1,AIDi,2∈G1,Ti是当前时间戳,通信开销为3|G1|+|T|=3104 bits.由于该方案是基于身份的公钥密码体系的认证方案,公钥即为消息发送者的身份,因此,不需要另外统计公钥的长度.在文献[15]的方案中,请求消息由(IDi,vpki,Mi,ti,σi)组成,签名σi=(Ri,Si),其中Ri,Si∈G1,假名IDi=(IDi,1,IDi,2,Ti),其中IDi,1∈G1,IDi,2∈Zq*,Ti和ti是当前时间戳,公钥vpki∈G1,通信开销为4|G1|+|Zq*|+2|T|=4320 bits.在文献[19]的方案中,请求消息由(Fi,Pi,mi,σi)组成,签名σi=(Ui,Vi),其中Ui,Vi∈G1,假名Fi=(F1i,F2i),其中F1i∈G1,F2i∈Zq*,公钥Pi∈G1,通信开销为4|G1|+|Zq*|=4256 bits.在文献[21]的方案中,请求消息由(PSUIDi,vepki,msgi,ti,sigi,IDRs)组成.签名sigi=(Ui,Ti)∈G1,假名PSUIDi=(PIDi,1,j,PIDi,2,j,TPi,j),其中PIDi,1,j,PIDi,2,j∈G1,TPi,j和ti是当前时间戳,公钥vepki∈G1,RSU身份IDRs∈G1,通信开销为6|G1|+2|T|=6208 bits.在文献[22]的方案中,请求消息由(IDi,PKi,mi,σi)组成,签名σi=(Ri,Y1i,ui,wi),其中Ri,Y1i∈G,ui,wi∈Zq*,假名IDi=(ID1i,ID2i,Ti),其中ID1i∈G1,ID2i∈Zq*,Ti是当前时间戳,公钥PKi=(Xi,Ri)∈G,通信开销为4|G|+3|Zq*|+|T|=1792 bits.在本文方案中,签名σi=(Ui,vi),其中Ui∈G,vi∈Zq*,假名IDi=(IDi1,IDi2,Ti),其中IDi1,IDi2∈Zq*,Ti是当前时间戳,公钥Xi∈G,所以通信开销为3|G|+3|Zq*|+|T|=1472 bits.
在安全性方面,如表5所示,文献[5]中的方案无法抵抗类型I攻击者,文献[15,19]中的方案无法抵抗类型II攻击者,文献[5,19]中的方案无法保证车辆匿名性,文献[5,19]在可追踪性方面存在问题,而本文可以满足所有安全需求.

表5 安全性的比较Table 5 Comparison of security
由表2-表4可知,与现有的方案[13,15,19,21,22]相比,我们的方案的计算开销和通信开销表现更优.另外,相对于文献[5]提出的方案,我们不仅保证了本文方案的安全性,而且本文方案与文献[5]提出方案的计算开销基本持平.
8 结 语
针对车载自组网匿名认证效率较低以及条件隐私保护难以实现的问题,本文在Thumbur等人[5]方案的基础上提出了一种无双线性配对的无证书签名方案.本文方案不需要安全信道,解决了OBU和TA之间通信依赖安全信道的问题.在随机预言模型下,基于椭圆曲线离散对数问题证明本文方案具有不可伪造性.此外,本文方案还满足匿名性、可追踪性和不可否认性.性能分析表明,本文方案在计算开销、通信开销和安全性方面都具有一定的优势,适用于车载自组网中数据的安全共享.
在未来工作中,我们将会通过引入聚合技术来进一步降低RSU的计算代价,设计更高效地车载自组网认证方案.
