融合显隐式反馈的协同过滤推荐算法研究

张亚明，高忠萍，高祎晴，刘海鸥

1(燕山大学 经济管理学院，河北 秦皇岛 066004)

2(燕山大学 互联网+与产业发展研究中心，河北 秦皇岛 066004)

3(北京京东世纪贸易有限公司，北京 102600)

1 引 言

随着互联网中的信息数量呈指数增长，海量的信息与海量用户的匹配问题就显得至关重要，以推荐算法为核心的个性化推荐系统应运而生[1]，其致力于从海量数据中挖掘出用户真正感兴趣的信息，以解决当前信息爆炸带来的信息筛选难和推荐难的问题.在个性化推荐系统发展的过程中出现过很多推荐算法，包括协同过滤、混合推荐、基于内容、基于规则、基于人口统计的推荐算法.其中协同过滤是目前推荐算法中主流的种类之一，其优点是可以通过一些以统计学为基础的机器学习方面的算法来得到比较好的推荐效果，不需要掌握一些复杂的专业领域的知识，工程上容易实现，可以方便应用到产品中.目前协同过滤推荐算法已经成为大多数实际应用中的基础算法.

协同过滤推荐算法利用用户历史行为信息，对数据进行分析，得到用户与物品之间的关系，从而给出满足用户个性化需求的推荐列表.通常协同过滤的模型为m个推荐对象，n个用户的数据形成的评分矩阵，在该矩阵中一些用户并未对一些推荐对象进行评价，所以相对应的评分矩阵中有一些位置没有评分数据，此时需要利用已有的部分数据进行某种运算，尽量去预测那些空白的位置的用户和推荐对象之间的评分关系，为用户生成评分最高的前N个推荐对象并形成推荐列表.近年来，虽然针对协同过滤推荐算法中单独利用显式反馈或者隐式反馈的研究层出不穷，但并没有真正发挥出的推荐系统中的显隐式反馈数据所包含的全部价值，所以近年来一些学者一直在融合显隐式反馈的协同过滤算法上做出努力，但仍然存在一些问题和全新的方向等待进一步研究.

一般来说，协同过滤推荐主要包括以用户为基础、以推荐对象项目为基础、和基于模型的协同过滤.其中基于模型的协同过滤作为目前主流的协同过滤推荐的类型，在机器学习与数据挖掘方法的基础上，利用用户的历史行为数据构建出用户-推荐对象关系模型，并据此预测待推荐对象的用户评分，最后根据预测评分生成该用户的个性化推荐列表.矩阵分解方法由于容易用代码实现，并且实现时算法复杂度低，预测效果较好，从包括关联算法、聚类算法、回归算法等目前主流的基于模型的协同过滤算法中脱颖而出，受到了许多系统与应用开发公司的青睐.矩阵分解在推荐系统中表现在将用户-推荐对象反馈矩阵分解成用户特征矩阵和推荐对象特征矩阵，由于这些分解后的特征矩阵能更明显的反映出原矩阵的一些特征，所以矩阵分解方法在推荐算法中发挥出了巨大作用.由此可知，在矩阵分解方向上的基于模型的协同过滤算法在目前的个性化推荐系统中具有很大优势.但是之前的多数研究都是针对于单独显式反馈或者单独隐式反馈的算法模型，并且在显式反馈和隐式反馈数据利用上一直存在数据利用不合理、采样策略不科学等问题，所以对于融合用户显隐式反馈的算法还处于等待进一步研究的阶段.

目前最为常用的推荐算法为基于显式反馈的SVD推荐算法、基于正负反馈的PSVD推荐算法、基于显隐式反馈的SVD++推荐算法等，但是这几种推荐算法都存在一定的弊端.对于SVD算法来讲，SVD作为一个基本算法，原理不难，实现也很简单，但是其算法数据类型不全面，算法仅利用了用户反馈中的显式反馈数据，浪费了隐式反馈的数据资源.并且在显式反馈数据利用上面，没有把握住用户与推荐对象产生数据偏置的根本原因；对于PSVD算法来讲，PSVD是基于SVD算法进行的正负反馈层面的重新构建，所以PSVD同样具有SVD算法存在的缺陷；对于SVD++算法来讲，SVD++作为一种融合了显隐式反馈的基于评分预测和矩阵分解的协同过滤推荐算法，在数据利用方面添加了用户隐式反馈数据，弥补了在SVD算法存在的仅利用显式反馈数据的一大缺陷.但由于隐式反馈数据即用户-推荐对象操作数据的特殊性质，所以隐式反馈中缺失了负样本.总结来说，目前存在的推荐算法存在以下3点问题：

1)隐式反馈样本可信度低.未能考虑到隐式反馈中缺失值的价值，即忽略在隐式反馈数据处理上缺少负反馈样本的问题，因此未能充分发挥隐式反馈的作用.

2)显式反馈数据利用不科学，针对显式反馈的利用中，没有考虑到个体对于打分机制的宽容度差异，比如一些用户评分整体偏高应该针对为每个用户采用基线评估，如果将评分不加处理直接利用的话，显式反馈一定程度上反而会造成数据误差，失去了反映用户偏好的作用.

3)缺少正负反馈维度的区分与利用.忽略了用户自身偏好以及推荐对象自身特征的正负属性对于显隐式反馈的影响作用，缺少对于推荐对象态度(正负反馈)的区分和利用.即除了用户喜好不同外，商品所包含不同属性会也影响到评分的高低.

本研究通过建立显隐式反馈数据的利用规则，在用户喜好不同与推荐对象主属性不同会影响用户评分的认知基础上，将用户反馈在正负反馈的维度上进行矩阵分解，重新设计算法模型，努力解决现存算法在模型和实验中存在的数据利用不充分和采样策略不科学等问题，并且验证新算法的可行性与数据效果，从而在融合显隐式反馈的协同过滤算法模型中提供新的研究思路.希望将其应用于实际的推荐系统中，能够提高推荐平台对与用户进行个性化投放时的精准度，提升用户对推荐对象的满意度，为推荐平台实现个性化推荐与精准营销做出一定贡献.

2 相关工作

随着科技进步推荐系统的不断优化与创新，显式反馈与隐式反馈的互补关系对推荐效果的改善作用日益凸显[2].Yue Liu等为了解决传统算法的数据稀疏性，提出了一种基于多关系网络的的协同过滤推荐算法，该算法该算法在传统矩阵分解模型的基础上，通过综合多关系社交网络的用户偏好来获得信任度和信任度特征矩阵，然后通过社交特征矩阵、商品特征矩阵和用户评级偏好的相似性来预测商品等级[3].Robert M.Bell和Koren将用户是否评过分这个行为作为隐式反馈，并利用用户评过分的所有物品的隐因子来代表用户，利用奇异值分解和基于邻域的模型对显式与隐式反馈数据进行数据融合并且同时用于推荐任务，提出了非对称SVD和SVD++算法[4].Weike Pan将用户集和推荐对象集通过聚类算法中的最常用的K-means方法进行聚类操作，构建融合显隐式反馈的基于迁移学习的分解机模型，有效解决异构反馈的问题[5].Nathan N.Liu将显隐式反馈数据本身的差异加入模型中，从而构建出一种将显隐式反馈数据设置了不同的比例参数的协同训练的矩阵分解模型[6].Wook-Yeon Hwang发现有效的有效的变量选择可以提高预测准确性，并在协同过滤中以及目标市场中有重要作用.因此提出了两种变量选择的方式去提高协同过滤的精确度，能够有效地在目标市场中识别重要项目和用户[7].Sarwar等人为解决实际的用户评分矩阵存在稀疏性问题，将SVD 算法(即奇异值分解算法)引入了协同过滤系统并得到了比较满意的结果[8].

以上研究考虑到协同过滤推荐算法中矩阵评分稀疏性的问题、用户评分矩阵稀疏问题、显隐式反馈数据等的问题，通过引入SVD算法、SVD++算法、相对于较为紧凑的关系网络去解决算法中的稀疏性的问题，通过个人设定隐式反馈、考虑显隐式数据差异来解决算法数据的问题等.这些研究成果为之后的研究打下了坚实的基础.

国内很多学者针对于融合显隐式反馈的协同过滤推荐算法进行了不同方向的研究，其中包括解决算法本身缺陷问题、针对推荐列表排序问题、考虑用户相似度的角度、优化显隐式反馈数据利用规则等方向.在侧重于解决这个算法本身的缺陷问题方面：Guo等人通过融合显隐式反馈，利用奇异值分解的方式补充拓展了SVD++算法，并且通过实验数据表明该方法在解决数据稀疏和冷启动问题上相较于其他方法有更好表现[9].在侧重于推荐对象个性化排序方面：李改[10]进一步将xCLiMF[11]和SVD++算法进行结合，通过对预期倒数排名指标进行最优化，构建了一个融合显隐式反馈的个性化排序模型MERR_SVD++.张阳[12]结合显隐式反馈数据，在SVD++算法和成对排序算法的基础上，根据当前预测出物品对的相对顺序来动态调整惩罚权重，加大对一些排序错误的物品对的惩罚力度，通过优化损失函数来训练相关参数，构建了自适应的成对排序推荐算法adapt AUC.在侧重于用户相似度以及信任关系方面：王东等人综合考虑了显隐式反馈信息，利用概率分解方法对商品评分矩阵和用户信任关系矩阵进行分解，然后加入用户操作记录，不断对模型参数进行优化训练，提高了模型预测能力[13].刘宏等人考虑到用户之间相似度存在差异，并且用户对推荐对象的评分时间或一些其他因素对用户评分会产生的影响，提出了一种基于加权相似度的整合显隐式反馈的协同过滤算法[14].在侧重于提高显隐式反馈数据利用方面：陈碧毅等人[15]首先利用加权低秩近似处理隐式反馈数据，训练出隐式用户与物品向量.然后引入了基线评估，同时将隐式用户与物品向量作为补充，通过显隐式用户与物品向量结合，训练得出用户对物品的预测偏好程度，提出了融合显隐式反馈的协同过滤推荐算法新方向.

当前对于协同过滤推荐算法的应用在各个方面都有涉及，徐建鹏，徐祥等就农户一般采用匿名网页直接浏览的方式查看农业新闻，显式反馈数据十分稀少，传统协同过滤推荐算法需要面临冷启动等问题，提出一种基于用户行为和新闻时效性的协同过滤推荐算法，通过对真实访问数据进行验证，结果表明提出的算法能有效提升农业信息推荐准确率[16].沙静，曾巩俐等就显式反馈数据不易获取、质量不好且易引起用户反感，使推荐结果不能满足用户需求等问题，提出一种基于隐式反馈数据的个性化游戏推荐方法，通过隐语义推荐算法实现了游戏的个性化推荐，并证明了该方法的精确率和召回率均优于其他方法[17].可见，生活中各个方面因为大数据的存在，都有可能应用到协同过滤推荐算法.

以上算法虽然从不同角度对融合显隐式的协同过滤推荐算法进行优化研究，但是多数都是在协同过滤推荐算法中运用矩阵分解方向上做出的一些改进与优化.无论是侧重于推荐对象之间的排序，还是用户之间的相似度，都是致力于从用户的隐式反馈信息中挖掘出更加准确的用户偏好特征信息，所以以上多数算法都在最基础的源数据利用层面存在一系列问题：显式反馈数据利用不科学、隐式反馈样本可信度较低等.因此，本研究基于SVD++算法模型，利用基准预测思想[18]在显隐式反馈中建立正负反馈的区分标准，得到基于正负反馈的用户和推荐对象特征矩阵，并且利用PSVD核心思想，构建一种新的融合显式反馈与隐式反馈的协同过滤推荐算法PNF_SVD++.并且获取真实数据对新算法进行试验，通过与其他算法(包括SVD++、PSVD)对比一些指标(包括MAE、RMSE)对实验模型进行验证.

3 相关理论基础

3.1 相关概念介绍

1)用户反馈：推荐系统的主要功能是从海量的待推荐对象中发现用户真正感兴趣的内容并进行推荐.而要对每位用户进行兴趣挖掘，就需要预先获取用户的历史行为进行数据分析与挖掘.用户反馈是最容易获取并且能够真实表达用户主观意愿的一部分用户历史行为数据，在推荐系统中，用户反馈根据判定方式和数据包含内容的不同，包括显式反馈与隐式反馈两类.而根据用户反馈时的主观意愿与情绪表达的不同，可以将用户反馈分为正反馈与负反馈两类.

2)显式反馈：显式反馈是指用户主动或者在一定的提示和指引下，根据自身偏好对某个推荐对象或者某种服务的主观使用或者体验感受进行打分、评级或是进行语言评价等行为，以此来很明显地表达用户体验感受和偏好程度.虽然显式反馈的种类比较有局限性，但由于显式反馈是由用户根据主观意愿自行填写，反映出的用户兴趣偏好的可信度较高，所以能够相对减轻数据预处理给推荐系统带来的压力.但是也正是因为这种显式反馈数据的收集完全依赖于用户的主动配合，所以想要在现实生活中获取大量保证数据的真实性与准确性的用户显示反馈也较为困难.并且这种数据的敏感性也逐渐导致了一些用户对于隐私安全的担忧，由此可能恰恰会破坏显示数据的真实性.

3)隐式反馈：与显式反馈不同，隐式反馈是在用户并不知情的情况下，系统记录的用户在系统中的所有操作行为数据[19].这些行为包括观察用户对一些推荐对象是否进行点击、点击次数、点击深度、浏览时长、是否进行收藏等.隐式反馈收集简便并且收集成本较低，但是收集到的信息通常包含很多关联性小甚至完全冗余的信息，比如误触操作，这种数据噪音在隐式反馈数据中是较难进行准确识别的，这样都会增加推荐算法完成推荐任务的难度.除此之外，显式反馈可以从数据中区分出正负样本，但这在隐式反馈中只能分辨出正样本，所以缺少负样本是目前针对于隐式反馈的利用中一个很普遍的问题.并且这些用户行为数据都是用户在某一个状态或者某段时间内的兴趣表现，在进行操作的时候也是一些推荐对象之间的相对比较，用户表达出的含义并不明确，所以从这些数据中很难推断用户的短期兴趣和长期兴趣，适应性较差也是隐式反馈利用的一个较大的问题.

4)正反馈：正反馈是经典控制论中的术语，当反馈信号与输入信号同属于相同方法时，称这种反馈信息为正反馈.对于推荐系统的用户反馈中的正反馈，它是通过制定一定的用户标准来划分出用户喜欢的推荐对象.通过不断找到用户的正反馈推荐对象，从中提炼出用户真正的兴趣特征，利用这些兴趣特征进一步为用户推荐真正喜欢的推荐对象，提高用户的个性化推荐体验.

5)负反馈：负反馈与正反馈为相对概念，前者目的在于通过信息进行一定操作，促使某功能输出与该功能目标的误差减小，使得该功能的真实作用稳定发挥；后者致力于使偏差不断增大，从而放大某些功能中的控制作用.对于推荐系统的用户反馈中的负反馈，它是通过制定一定的用户标准来划分出用户不喜欢的推荐对象.通过不断找到用户的负反馈推荐对象，从中提炼出用户不感兴趣的推荐对象特征，利用这些用户的厌恶特征进一步为用户筛选屏蔽掉包含这些厌恶特征的推荐对象，保证推荐系统给用户推荐的推荐对象不会引起用户反感，促进推荐算法不断补充与优化.

3.2 相关算法介绍

3.2.1 基于显式反馈的SVD推荐算法

协同过滤的评分预测问题视为矩阵填充问题，但是由于实际的用户评分矩阵存在稀疏性问题，研究人员将SVD 算法(即奇异值分解算法)引入了协同过滤系统并得到了比较满意的结果.该模型是把初始的评分矩阵分解为两个特征矩阵，但是仍然缺少对用户和推荐对象的偏置处理.所以目前的SVD算法是结合了基准预测模型和隐因子模型，所以SVD算法的评分预测函数定义为公式(1)：

rui′=μ+bu+bi+Pu×QTi

(1)

其中μ表示预测基准，该预测基准一般取评分矩阵的平均值，bu和bi分别表示第 u个用户和第i个推荐对象的评分偏置，Pu表示用户特征矩阵的第u行，Qi表示推荐对象特征矩阵的第i行.

此时最优化目标函数为公式(2)：

(2)

通过基准预测模型计算出用户偏置bu和推荐对象偏置bi，将其视为已知项，可以不为其引入正则项，因此目标函数可以改写为公式(3)：

(3)

与隐因子模型中求解算法相同，利用随机梯度下降法优化目标函数，可得到Pu和Qi，进而可以针对用户的待推荐对象进行评分预测，将评分较高的前N个推荐对象作为该用户的推荐列表.

3.2.2 基于正负反馈的PSVD推荐算法

在SVD算法的基础上，虽然在评分预测函数中在评分预测公式中加入了用户偏置和物品偏置，但是这种添加作用只是在函数中添加了两个待训练的参数，并没有利用好预测结果会发生偏倚的主要原因.并且在现实生活中，商品所包含的不同属性会影响用户对其评分的高低.如果物品的主属性是用户喜欢的，则会得到用户较高评分，物品的主属性是用户不喜欢的，则会得到用户较低评分.PSVD算法是在SVD算法的基础上，利用矩阵分解方法，通过建立标准，区分出用户喜欢与不喜欢的推荐对象评分矩阵，对应称为正反馈评分矩阵和负反馈评分矩阵.通过区分用户的喜好来提高评分预测的准确度，取得了理想的效果.

PSVD算法具体求解过程为：首先制定标准划分正负反馈划分标准，为每一个评分rui找到一个基准值μui，当rui>μui时，该物品进入正反馈评分矩阵；否则，被分入负反馈评分矩阵.然后将得到的正负评分矩阵进行预处理，令Rp′=Rp-U×Ip，Rn′=Rn-U×In.其中Rp表示正反馈矩阵，Rn表示负反馈矩阵，U表示基准值μui组成的矩阵，Ip和In表示正负反馈矩阵的标示矩阵.所以PSVD算法的评分预测函数定义为公式(4)：

rui′=μ+bu1+bi1+Pu1×QTi1+bu2+bi2+Pu2×QTi2

(4)

其中bu1+bi1+Pu1×QTi1=Rp′，bu2+bi2+Pu2×QTi2=Rn′.

此时目标函数为公式(5)：

min∑(u，i)∈T(rui-μ-bu1-bi1-Pu1×QTi1-bu2-bi2-
Pu2×QTi2)2+λ(b2u1+b2i1+P2u1+Q2i1+b2u2+b2i2+P2u2+Q2i2)

(5)

继而利用随机梯度下降法求解目标函数得到最优解bu1、bi1、bu2、bi2、Pu1、Qi1、Pu2、Qi1，则可以通过评分预测公式针对用户的待推荐对象进行评分预测，将评分较高的前N个推荐对象作为该用户的推荐列表.

3.2.3 基于显隐式反馈的SVD++推荐算法

相比于显式反馈数据，隐式反馈数据存在无法准确表达用户偏好程度、数据处理缺少负反馈样本、数据噪声处理困难等缺陷，但是相对应的隐式反馈数据量大并且更稠密、更稳定，并且由用户自然产生的数据，通常更会真实地反映用户态度.所以对于隐式反馈数据的利用对协同过滤推荐算法的研究来说非常有必要的.经典的 SVD 算法以及SVD算法的一些变形都是基于显式反馈做出的研究，一种同时考虑用户显式反馈与隐式反馈的SVD++算法模型随之产生.对用户评分预测函数定义见公式(6)：

(6)

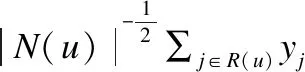
如公式(7)考虑利用目标函数进行优化：

min∑(u，i)∈T(rui-μ-bu-bi-(Pu+

(7)

(8)

首先求出预测基准值μ，按照基准预测模型求出bu和bi值，然后利用随机梯度下降法优化目标函数，最后得到Pu、Qi和yj，则可以针对用户的待推荐对象进行评分预测，将评分较高的前N个推荐对象作为该用户的推荐列表.

通过对于现存协同过滤推荐算法的研究，显式反馈数据利用不合理的根本问题在于对于基准预测思想并未充分利用，改进思路还是从基准预测思想入手，主要是在显式反馈数据利用上，重新构建基准预测计算方法.在添加用户偏置和推荐对象偏置的基础上，设置用户偏好参数来衡量用户喜好；隐式反馈数据缺少负反馈样本的根本问题在于对于缺失值的利用上不够合理，既不能直接全部否定缺失值的利用价值，又不能全部直接利用.应构建一个区分方法，利用用户既存在对某个推荐对象不感兴趣所以并未点击的可能性，加之存在用户并没有看到某个推荐对象的可能性的概念，在缺失值的利用中添加权重的概念，更加科学的从缺失值中得到用户负反馈样本.

4 问题的形式化定义

4.1 符号定义

表1为本文算法会用到符号所代表的含义.

表1 PNF_SVD++算法中相关符号定义Table 1 Definition of related symbols in PNF_SVD++algorithm

4.2 问题定义

融合显隐式反馈的协同推荐算法结合了基准预测模型、隐因子模型，融合显示反馈与隐式反馈数据，将用户-推荐对象评分矩阵R其划分为正反馈与负反馈用户评分矩阵，构建新的评分预测模型.该算法的目标是，给定一个用户u，从用户u的待推荐对象集合中选择一个推荐对象i，帮助系统根据已知用户历史行为数据信息来预测出用户u对推荐对象i的评分rui，即偏好程度.进而根据每个用户的预测评分由高到低对推荐对象进行排序，将预测评分较高的前N个推荐对象形成用户u的推荐列表.

显式反馈数据中，用户对推荐对象的评分信息用矩阵R=[rui]m×n表示，rui代表用户u对推荐对象i的评分信息，评分越高代表用户对该推荐对象越满意.例如，在5分制的电影评分系统中，rui={1，2，3，4，5}，评分越接近5代表用户越喜欢该电影，评分越接近1，代表用户对该电影越不感兴趣.显式正反馈用户特征矩阵用Pu1表示，显式负反馈用户特征矩阵用Pu2表示，显隐式正反馈推荐对象特征矩阵用Qi1表示，显隐式负反馈推荐对象特征矩阵用Qi2表示，实际的用户-推荐对象评分矩阵R可由Pu1×QTi1+Pu2×QTi2近似表示.评分rui已知的用户-推荐对象对(u，i)存储于集合T={(u，i)|rui≠0}中.

用户u对推荐对象i的评分特异性用评分基线bui表示，其由所有物品的评分基线μui、用户u评分的正反馈偏置bu1、用户u评分的负反馈偏置bu2和推荐对象i评分的正反馈偏置bi1、推荐对象i评分的负反馈偏置bi2之和构成，即bui=μui+bu1+bi1+bu2+bi2.

5 融合显隐式反馈的协同过滤推荐算法

PNF_SVD++算法主要设计思路为：已知SVD++算法是一种利用评分预测和矩阵分解方法的融合了显隐式反馈数据的协同过滤算法.其思想是利用用户特征矩阵与推荐对象特征矩阵算出用户评分矩阵，从而算出某个用户对某个推荐对象的预测评分值.其中用户特征和推荐对象特征需要从用户的显隐式反馈中进行挖掘.在挖掘用户特征和推荐对象特征的过程中，区分为正反馈矩阵(用户喜欢)和负反馈矩阵(用户不喜欢).所以需要利用基准预测思想，找到每个用户显式反馈评分基准值与隐式反馈中的行为信息区分标准，对用户正负反馈矩阵进行区分.进而设计出一种在SVD++算法基础上的利用用户正负反馈特征的新型协同过滤推荐算法称为PNF_SVD++.

具体PNF_SVD++算法的技术路线如图1所示，基于上文设计思路，将本文主要先从解决目前算法缺陷出发，制定在全反馈层面区分用户偏好即用户-推荐对象正负反馈矩阵的标准，分为显式反馈基准计算方法和隐式反馈区分用户偏好标准，然后利用该标准从显隐式反馈数据中计算出显式正负反馈用户-推荐对象评分矩阵与隐式正负反馈用户-推荐对象操作矩阵，进而求出显隐式正负反馈用户特征矩阵与推荐对象特征矩阵，由此将以上得到的特征矩阵进行参数优化计算出显隐式正负反馈中的用户偏置与推荐对象偏置，最终得到评分预测公式，并利用公式进行计算即可得到用户对于推荐对象的预测评分，进而生成个性化推荐列表.

图1 技术路线图Fig.1 Technology roadmap

5.1 区分用户偏好标准

(9)

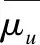
(10)

其中Zui表示用户u对推荐对象i的满意概率，rui表示用户u对推荐对象i的评分，rmax用户u给出过的最高评分.Iui为指示函数，如果rui≠0，则Iui>0，否则Iui=0.

同样，隐式反馈数据也需要区分出正、负反馈用户评分矩阵.即A=Aui1+Aui2，其中A为用户-推荐对象操作矩阵，Aui1为隐式正反馈用户-推荐对象操作矩阵，Aui2为隐式负反馈用户-推荐对象操作矩阵.如公式(11)考虑利用目标函数进行优化：

(11)

为了解决隐式反馈数据缺少负反馈样本的问题.利用WALS算法[21]思想，从缺失值中区分正负反馈样本.设置Aui=1为正样本，即用户u对该推荐对象i进行了点击.根据用户对推荐对象进行过评分恰好可以反映出一定的用户偏好的基本设定，用户对其进行过评分那就意味着一定进行过点击，说明用户对该推荐对象有一定的偏好，此时该种推断具有很强的可信度，设其权重Wui=1.而对于缺失值来说，设置Aui=0，即用户u对该推荐对象i没有进行过点击，其代表负反馈样本的可信度较低，只能够定义这些推荐对象可能为负反馈样本，设置其权重Wui=δ∈[0，1]，如公式(12)所示：

(12)

其中，当δ=0，说明所有缺失值都无法进行判断，则无法区分出负反馈样本，即所有样本都为正反馈样本.当δ=1，说明所有缺失值可以确定为负反馈样本.得到权重矩阵所以更新目标函数为公式(13)：

(13)

由于A与W皆为稠密矩阵，采用GALs算法[22]分解加权矩阵W，用两个低秩矩阵的乘积XYT近似加权矩阵W，已知其中正样本的权重为1.所以再次更新目标函数，如公式(14)所示：

(14)

利用随机梯度下降法进行求解Au1和Au2.步骤如下：

1)初始化Au1和Au2，并且设定合适的学习速率α2和正则化参数λ2.

3)更新Aui1←Aui1-α2∇Aui1和Aui2←Aui2-α2∇Aui2.

4)一直重复计算Aui1和Aui2下降梯度并更新Aui1和Aui2，直到Aui1和Aui2的变化小于某个设定阈值.

5.2 计算反馈特征矩阵

预测基准值同时也作为显式反馈区分用户偏好的用户评分基准值μui，即当rui>μui时，该评分表示用户喜欢该推荐对象，将其归入正反馈评分矩阵；否则，将其加入负反馈评分矩阵.所以可以初步得到显式正、负反馈用户-推荐对象评分矩阵Rui1与Rui2，即R=Rui1+Rui2，其中R为显式用户-推荐对象评分矩阵.然后需要对得到的Rui1与Rui2进行预处理.Rui1′=Rui1-U×Iui1，Rui2′=Rui2-U×Iui2.其中U表示预测基准μui的标示矩阵，即当Rui1对应值不为空时，Iui1对应位置标示为1.并且运用SVD模型思想，设Rui1′与Rui2′为公式(15)与公式(16)：

Rui1′=bu1+bi1+Pu1×QTi1

(15)

Rui2′=bu2+bi2+Pu2×QTi2

(16)

其中Pu1为显式正反馈用户特征矩阵，Pu2为显式负反馈用户特征矩阵，Qi1表示显式正反馈推荐对象特征矩阵，Qi1表示显式负反馈推荐对象特征矩阵.此时由于Rui1′与Rui2′可视为已知量，所以可有最优化目标函数为公式(17)与公式(18)：

(17)

(18)

同理利用随机梯度下降法可以分别求出Pu1、Qi1、Pu2、Qi2.同样通过计算可以得到隐式正负反馈用户-推荐对象操作矩阵，运用SVD++算法中关于隐式反馈的模型思想，设Aui1与Aui2如公式(19)与公式(20)所示：

(19)

(20)

则设最优化目标函数如公式(21)与公式(22)所示：

(21)

(22)

利用随机梯度下降法可以分别求出Yj1、Yj2，计算过程同上.

5.3 建立评分预测模型

基于以上算法基本定义与重点用户偏好区分方法介绍，并从显式正负反馈用户-推荐对象评分矩阵和隐式正负反馈用户-推荐对象操作矩阵中求出显隐式正负反馈用户、推荐对象特征矩阵，由此建立评分预测排序模型为用户进行推荐.得到评分预测模型，如公式(23)所示：

(23)

对应其目标函数为公式(24)：

(24)

利用随机梯度下降法优化目标函数，一直重复计算bu1、bi1、bu2、bi2、Pu1、Qi1、Yj1、Pu2、Qi1、Yj2，直到参数变化小于某个设定阈值.最后使用评分预测公式针对用户的待推荐对象进行评分预测，返回预测评分较高的前N个待推荐对象作为该用户的推荐列表.

5.4 PNF_SVD++算法具体步骤

PNF_SVD++算法的具体步骤如下：

PNF_SVD++算法：

输入：显式反馈用户-推荐对象评分矩阵R=[rui]m×n，隐式反馈用户-推荐对象操作矩阵A=[Aui]m×n.

3.ReturnRui1′，Rui2′

5.L=∑u，iWui(Aui-Aui1-Aui2)2+λ2(Aui12+Aui22)

6.InitializeAu1，Au2

7.repeat

8.Draw(uid，iid，rating)randomlyforA

9.Aui1←Aui1-α1∇Aui1

10.Aui2←Aui2-α1∇Aui2

11.untilconvergence

12.ReturnAu1，Au2

13.InitializePu1，Qi1，Pu2，Qi2，bu1，bi1，bu2，bi2，Yj1，Yj2

14.repeat

15.Draw(uid，iid，rating)randomlyforRui1′+Au1

16.Pu1←Pu1-α1∇Pu1

17.Qi1←Qi1-α1∇Qi1

18.Yj1←Yj1-α1∇Yj1

19.bu1←bu1-α1∇bu1

20.bi1←bi1-α1∇bi1

21.Draw(uid，iid，rating)randomlyforRui2′+Au2

22.Pu2←Pu2-α2∇Pu2

23.Qi2←Qi2-α2∇Qi2

24.Yj2←Yj2-α2∇Yj2

25.bu2←bu2-α2∇bu2

26.bi2←bi2-α2∇bi2

28.eui=γui-γui′

29.untilconvergence

30.ReturnPu1，Qi1，Pu2，Qi2，bu1，bi1，bu2，bi2，Yj1，Yj2

31.end

6 实验分析

本研究的实验数据均从开源的MovieLens数据集中获取.该数据集由Grouplens小组在不同时期从MovieLens网站中收集而来，并广泛应用于推荐系统算法实验中.由于实验条件限制，本次实验选择MoviLens数据集中大小为1M的数据包ml-lastest-small进行算法验证，该数据集更新时间为2018年9月.该数据集中包含了600个用户将100000个收视率和3600个标签应用于9000部电影，共计100837条评分记录.并且每位用户都有至少20条评分记录，评分的范围是0-5分，这其中评分越高则说明用户对电影的喜爱程度越高.

本实验中数据抽取方法为抽取80%作为训练集数据，剩下的20%的数据作为测试数据.本实验将评分行为视为一种隐性偏好的表现，即不论用户为推荐对象i评分的高低，本实验都将视为用户对该推荐对象存在隐性的偏好，将其视为用户对推荐对象的点击操作行为.

6.1 实验设计

本次实验利用可扩展开发平台Eclipse 2020-03版本，使用python作为开发语言，基于PNF_SVD++算法思路，设计如下试验方案：

首先，对数据集进行数据清洗、数据存储形式转换为评分矩阵形式、训练集和测试集的数据划分等预处理操作.其次，加载处理后的训练集，确定所需参数，按照算法步骤分别利用训练集中数据，求出所需正负反馈用户-推荐对象矩阵，并进一步求出所需相关特征矩阵，并建立PNF_SVD++算法核心评分预测模型，计算MAE、RMSE两个评价指标.最后，利用同样测试集对PSVD、SVD++等相关算法进行实现，并且修改相关参数与PNF_SVD++算法实验中保持一致，分别对MAE、RMSE两个评价指标进行数据验证，将数据结果与PNF_SVD++算法进行对比验证.在协同过滤算法中，验证评分预测准确性的指标一般有MAE和RMSE.MAE(Mean Absolute Error)即平均绝对误差，用于计算测试集中所有预测评分误差之和的平均值.当MAE值越小，表示预测评分误差越小，则说明算法预测的准确度越高.RMSE(Root Mean Squared Error)即均方根误差，用于计算测试集中预测误差平方和均值的平方根.与MAE类似，RMSE值越小，说明预测评分与真实评分越接近，则说明算法预测的准确度越高.MAE与RMSE计算公式如下：

(25)

其中Test为测试集，γui为测试集中的任意一项评分，γui′为算法预测得到的评分.

(26)

其中Test为测试集，γui为测试集中的任意一项评分，γui′为算法预测得到的评分.

6.2 结果分析

本次实验中，将PNF_SVD++算法与PSVD算法和SVD++算法进行对比，统一参数为：正负反馈学习速率l1=l2=0.01、学习速率迭代参数0.93、正则化系数λ=0.15、以及影响实验的关键指标为矩阵分解降维参数K与优化损失函数的随机梯度下降的迭代次数T，分别设置当T=5时，K为10、20、30、50，当K=30时，T为5、10、20、30.

由表2可知，在T取5时，在一定范围内，随着K逐渐的增大，PNF_SVD++算法、SVD++算法和PSVD算法平均绝对误差和均方根误差的值均逐渐减小，说明实验结果与实际结果吻合度逐渐增加，算法发挥出真实的价值.同时，在T取5，K取定值5、10、20或30时，PNF_SVD++算法的平均绝对误差和均方根误差均小于SVD++算法和PSVD算法，说明PNF_SVD++算法的精确度更高，表现力更加优秀.

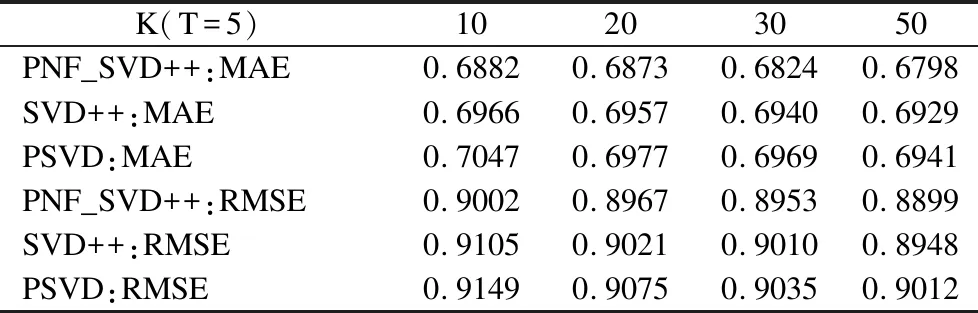
表2 矩阵分解降维参数K对实验结果的影响Table 2 Influence of matrix factorization dimensionality reduction parameter K on experimental results

由表3可知，在K取30时，T取不同的值时，PNF_SVD++算法、SVD++算法和PSVD算法的表现力是不同的.在一定的范围内，随着迭代次数的增加即T越来越大时，各个算法的误差都是逐渐减小的.当K取定值30，T取5、10、20或30时，PNF_SVD++算法的平均绝对误差和均方根误差均小于SVD++算法和PSVD算法，说明在降维参数K不变时，在相同的迭代次数T下，PNF_SVD++算法的效果优于SVD++算法和PSVD算法.

表3 随机梯度下降的迭代次数T对实验结果的影响Table 3 Effect of stochastic gradient descent iteration number T on experimental results

得到上述结论之后，为了避免数据量过小带来的实验误差，本研究再次使用Movielens 1M Datasets数据集中大小为6M的数据包ml-1m进行二次算法验证，其中包含由2000年加入MovieLens的6，040个MovieLens用户对约3，900部电影的1000209条匿名分级评价.

从图2和图3显示的实验结果可知，在T取定值时，随着K值的变化，PNF_SVD++算法的平均绝对误差和均方根误差均小于SVD++算法和PSVD算法.在K取定值时，随着T值的变化，PNF_SVD++算法的平均绝对误差和均方根误差也均小于SVD++算法和PSVD算法.由此可知，PNF_SVD++算法实验结果表现依然优于SVD++算法及PSVD算法，但是可以发现整体数据误差较MovieLens Latest Datasets数据集数值偏大，是因为Movielens 1M Datasets数据集中分级评价结果精确到个位，MovieLens Latest Datasets数据集中的分级评价精确到十分位，从而导致3种算法误差较之前数据集稍微增大，但不影响PNF_SVD++算法优越性的验证.另外可以发现在该数据集表现中，K=10-K=30时误差逐渐减小，K=50时误差增大，更加验证了用户反馈矩阵的矩阵分解降维参数K对于算法精准度的贡献需要限制在一定范围内.

图2 矩阵分解降维参数K对实验结果的影响Fig.2 Influence of matrix factorization dimensionality reduction parameter K on experimental results

图3 随机梯度下降的迭代次数T对实验结果的影响Fig.3 Effect of stochastic gradient descent iteration number T on experimental results

综上，在相关参数统一时，PNF_SVD++算法与PSVD和SVD++算法相比，预测评分的误差更小，即推荐精准度更高.这在算法实现层面上，证明了PNF_SVD++算法确实可以为用户形成一个误差更小的排序敏感推荐列表(比如top-N推荐列表)，其具有更好的预测效果和实践效果，也说明PNF_SVD++算法具有真实可行性与有效性.在算法设计层面上，一是证明了针对显式和隐式数据制定不同的数据处理以及挖掘规则，能够有效提高数据利用效率，使得数据利用更加科学，减少数据冗余浪费以及噪声数据污染实验的情况；二是证明了在融合显式和隐式反馈数据的基础上进行正负反馈的区分与处理，关注显隐式反馈数据中隐含的偏好关系，挖掘出更加符合实际推荐场景的偏好关系，都能够有效降低评分预测误差，使得预测结果更加贴近真实数据.

以上分析都表明围绕正负反馈思想的PNF_SVD++算法降低了预测误差，提高了推荐精度，并且符合实际推荐场景，为融合显隐式反馈的协同过滤推荐算法提供了一种在正负反馈层面上的新的研究方向.

7 结 论

个性化推荐系统合理利用显隐式反馈可以有效提升推荐系统的性能，但是目前融合显隐式反馈的推荐算法发展仍存在显式反馈数据利用不合理、隐式反馈缺乏负反馈样本等问题，并且没有在全反馈层面上进行正负反馈层面上的尝试.为解决以上问题，本研究主要是通过完善基准预测公式，解决当前PSVD算法以及SVD++算法中显式反馈数据利用不合理的问题；以及通过制定隐式反馈数据偏好区分标准，在隐式反馈数据的缺失值的处理上进行优化.并且在解决当前算法存在的问题的基础上，融合显隐式反馈数据后充分利用′将用户整体偏好分为正负反馈再分别进行评分预测′的思想，重新优化基于显隐式反馈的协同过滤算法模型，构建了一种融合显隐式反馈的基于正负反馈的协同过滤推荐算法PNF_SVD++，解决了当前算法模型中显式反馈数据利用不合理以及隐式反馈数据缺少负样本的问题.同时通过具体的实验验证了PNF_SVD++算法对比PSVD算法与SVD++算法评分预测误差较小，说明PNF_SVD++算法具有可行性与有效性，为融合显隐式反馈的协同过滤推荐算法提供了一种在正负反馈层面上的研究方向.

由于实验设备和时间限制，对算法参数验证范围较小，同时针对于隐式反馈数据在正负反馈层面的区分，由于开源数据集中得到的都是显式数据，在实验中将分数抹去后作为隐式反馈数据，实验数据有过于理想之处，所以日后希望用真实企业数据，将算法真正应用到实际场景中.