基于贝叶斯博弈的防御资源调配模型研究

黎忠凯，齐向伟，王 鑫，霍程程

（1.新疆师范大学 计算机科学技术学院，新疆 乌鲁木齐 830054；2.新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830054）

0 引 言

一个城市内如何优化有限的防守资源来抵御潜在的攻击对公共安全部门来说是一个巨大的挑战。一些研究学者已经使用贝叶斯博弈模型来解决攻击者的问题。文献[2]提出了一系列贝叶斯斯坦伯格博弈模型，并将其应用于洛杉矶国际机场和联邦空管局，优化了其安全资源配置；文献[3]构造了一个静态贝叶斯博弈模型来模拟网络信息系统的主动防守策略，但是该方法仅考虑了静态环境下的博弈，忽略了现实情况下可能存在的状况；文献[4]提出了一种基于完整信息博弈论的有限防御资源分配优化方法。该方法充分考虑了防御者和攻击者之间的战略互动，可以确定防御资源的最佳全局分配。但是，此方法仅考虑游戏模型中的一种攻击者。借鉴相关研究的经验，本文在原有的贝叶斯博弈模型的基础上进行改进，将一种攻击者类型的研究扩展为针对多种攻击者类型的研究，保护加油站免受多种类型攻击。据了解，在一个城市范围内，研究使用博弈论优化加油站防御资源配置的报道比较少。

综上所述，本文基于贝叶斯博弈模型提出了一种考虑多种类型攻击者的优化有限防御资源调配的博弈论方法，该方法引进先验概率，通过优化防御资源调配最小化预期损失。以4 个贮存汽油、柴油的加油站为例，本文验证了该方法的可靠性以及适用性，比较了不同防守策略的效果，并说明了该方法的优越性。

1 模型构建与分析

1.1 符号及定义

为了方便分析，本文出现的数学符号定义见表1。

表1 有关符号及定义

1.2 参与者的策略集与收益

针对潜在攻击的情况，本文为保护多个加油站设施研究了防御资源的分配方法，并将其作为博弈的双方参与者：攻击者和防守者。攻击者通过选择一个合适的目标最大化他的预期收益，而防守者的目标就是通过优化防守资源配置最小化预期损失。

一般来说，攻击者假定认为在一个时间段只能攻击一个目标。对于个加油站，攻击者的策略可以用一个概率集描述：

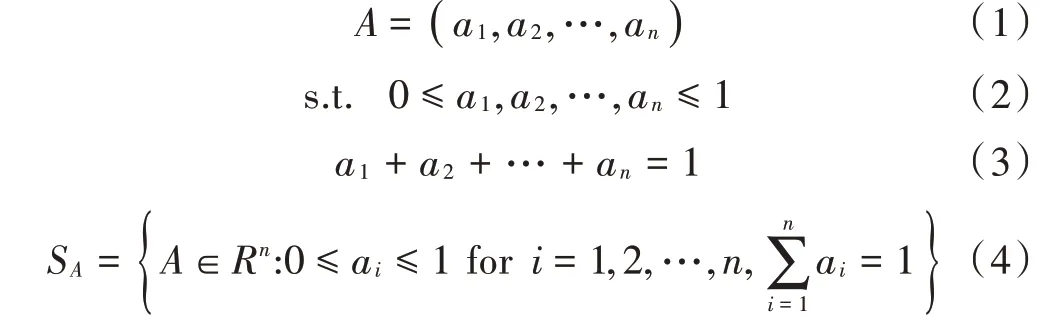
对于防守者来说，这个策略可以表示为可用资源的调配模式：

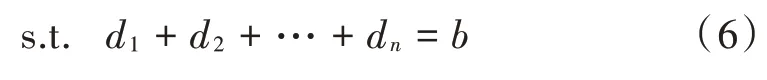
防守者的策略集描述如下：

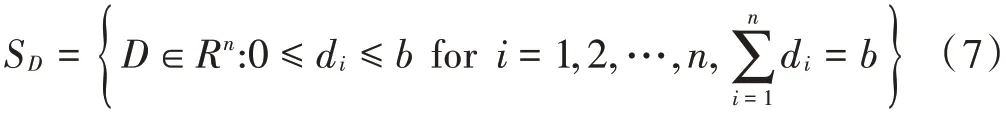
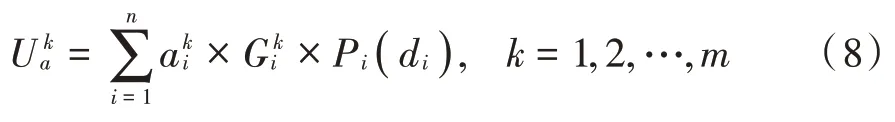
防守者的预期损失和收益可以表示为：

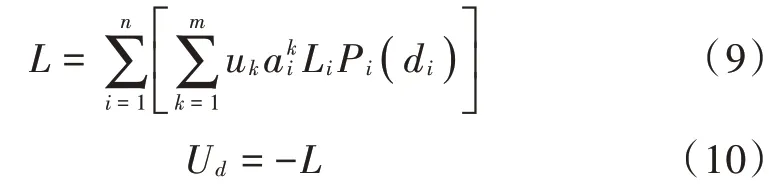
1.3 模型构建

目前的贝叶斯博弈模型中，攻击者通过选择一个合适的攻击目标来最大化自己的预期收益，本文将攻击者A的优化问题表示为：

与此相反，防守者的目标就是通过优化有限的防御资源配置来抵御各种类型的攻击者，从而最小化他们的预期损失：

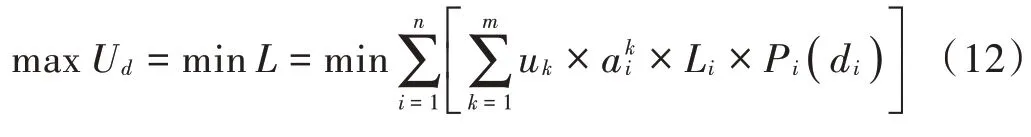
目前的贝叶斯博弈模型是指参与者们彼此都无法观察到对方的策略，从而根据观察到的信息决定自己的策略。将这种静态贝叶斯博弈模型用海萨尼将其转换为一个完全信息博弈求解，可以表示为(,,,…,a)。当纳什均衡实现时，防守者是无法通过改变自己的防守策略从而进一步减少自己的预期损失，攻击者也无法通过改变自己的攻击策略从而进一步扩大自己的预期收益。因此，此时贝叶斯纳什均衡需要满足下面两个公式：

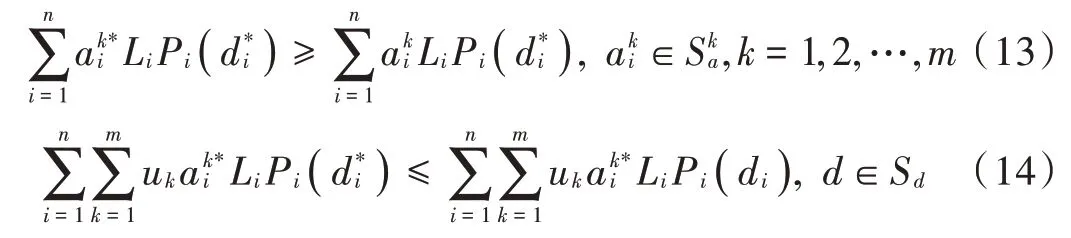
本文根据上述已有的贝叶斯博弈方法，考虑多种攻击类型情况，通过引进先验概率以及脆弱性函数对其进行优化，构建博弈方法如图1 所示。

图1 博弈论方法

该方法最显著的特点就是它考虑了现实中多种类型攻击者的存在，主要步骤如下：

1）结果估算：基于收集好的加油站和潜在攻击者的信息。

2）确定攻击者的类型和先验概率：随着信息的收集，防守者能够确定攻击者的类型并且推测出他们的先验概率。

3）评估攻击者眼中每个加油站的价值收益：防守者从攻击者的角度出发，评估每个加油站在不同攻击者眼中的价值。

4）建立防守者策略集：随着信息的收集，防守者们可以构建一个策略集（见式（7）），另外通过分析防御投入对脆弱性的影响，防守者可以确定各个加油站防御资源的脆弱性函数。

5）建立攻击者策略集：防守者推测每个加油站受到不同类型攻击者发动攻击的概率并且进一步为不同类型攻击者构造一个策略集（见式（4）和式（13））。

6）开发一个贝叶斯博弈模型：贝叶斯博弈模型的输入（见式（11）和式（12））包括攻防双方的策略集、结果、脆弱性、攻击者眼中加油站的价值以及不同类型攻击者的先验概率。

7）获取防御资源的最优配置：通过求解贝叶斯博弈模型，防守者可以得到一个贝叶斯纳什均衡解，也就是一个最优策略集。根据均衡解，防守者最后可以得到有限防御资源的最优配置。

2 实验设计

2.1 场景仿真

为了证明提出方法的可靠性和适用性，本文以4 个贮存汽油、柴油的加油站作为仿真案例进行研究。基本信息如表2 所示。

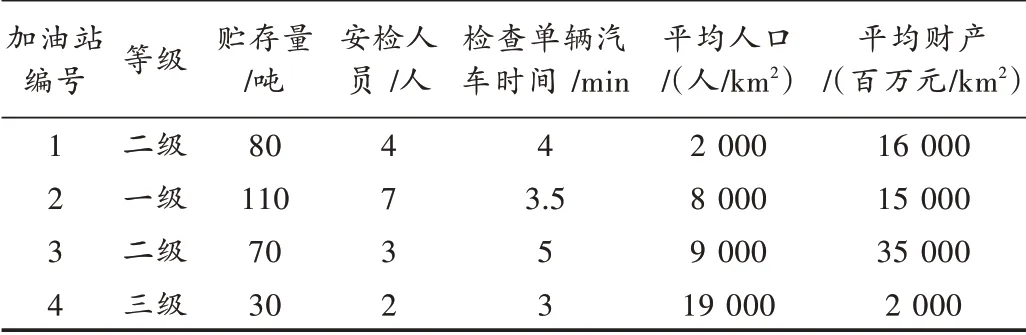
表2 加油站基本信息

与其他加油站相比，仿真场景中加油站拥有其独特之处。在进入加油站之前设有拦卡，车上人员需要下车接受检查后才能进站加油，这个过程中需要一定时间；根据加油站的大小不同，检查人员数量也不尽相同，工作效率也是相互不一的。但本文研究的主要目的是分析多种类型攻击者对防御资源分配的影响，因此假定加油站安检人员不具备抵御攻击者的防御能力，4 个加油站特点和安保措施大致相同，认为保护4 个加油站的困难水平是相同的；也就是意味着在给任何一个加油站增加防御资源时，加油站的脆弱性变化无异。根据上面的假设，可以引进脆弱性函数，将其描述为：

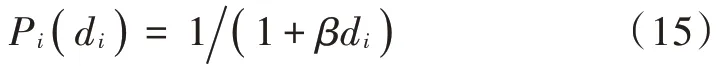
假设无论攻击者存在一种类型还是多种类型，防守者都知道每个加油站对于不同类型攻击者的价值，但是防守者不清楚哪种类型攻击者将会发动攻击，因此通过设置不同类型攻击者的先验概率确定每种类型攻击者将会发动攻击的可能性。在本文案例研究中，设置了三种类型攻击者、和，不同加油站在不同类型攻击者眼中的价值如图2 所示。

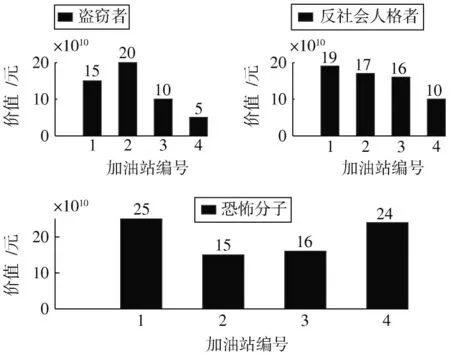
图2 攻击者眼中加油站的价值

图2 中：攻击者对4 个加油站的估值存在很大差异，相比攻击者和，他更倾向于对贮存油量更多的加油站发起进攻；而攻击者与攻击者恰恰相反，攻击者倾向于周边人口密度大的加油站，他的目的在于尽可能造成大的人员伤亡、人群恐慌和财产损失；相比之下，攻击者与攻击者对4 个加油站的估值基本相似，但是其行为难以猜测。

根据上述提到的多种类型攻击者，设置了3 个完整信息博弈和4 个贝叶斯博弈场景，对比两种博弈在优化前后防御资源配置上的差异，如表3 所示。在本文案例研究中，出于对安全的考虑，虚构了攻击者目标的价值和先验概率，虽然这些数据不满足实际应用的情况，但是已经满足了贝叶斯博弈模型的要求。

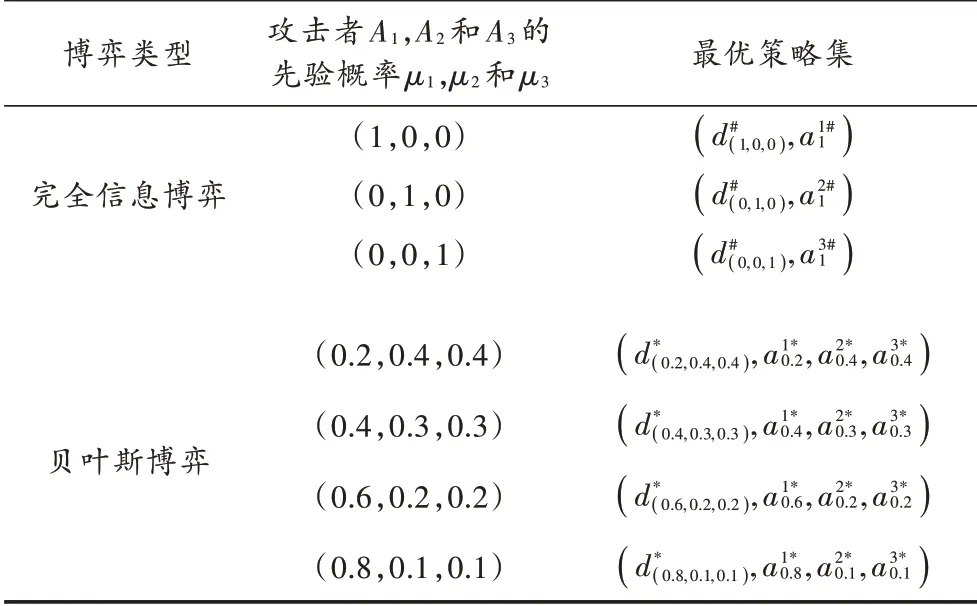
表3 两种博弈场景和最优策略集

2.2 损失评估

潜在攻击的结果可以从下面两个方面来考虑：人员伤亡和财产损失。简单来讲就是可以用人民币将人员伤亡转换为财产损失进行评估，因此其结果可以表示为：

式中：L是指第个加油站被成功攻击后的财产损失；L是指第个加油站被成功攻击后的人员伤亡，可以将其转换为财产损失。

综合当地政府安全部门和专家意见，本实验的计算方法中死亡、重伤和轻伤人员分别一一对应300 万元、100 万元和4 万元，这些价值与当地的经济条件、风俗有关，每个地方都不相同并且随着时间而变化。

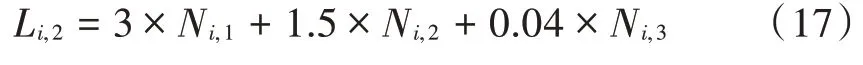
式中：N，N和N分别表示死亡、重伤和轻伤人员的数量。

模拟4 个加油站场景，平均人口密度和财产密度如表1 所示，任意一个加油站被成功袭击后的损失根据式（16）和式（17）计算，如图3 所示。

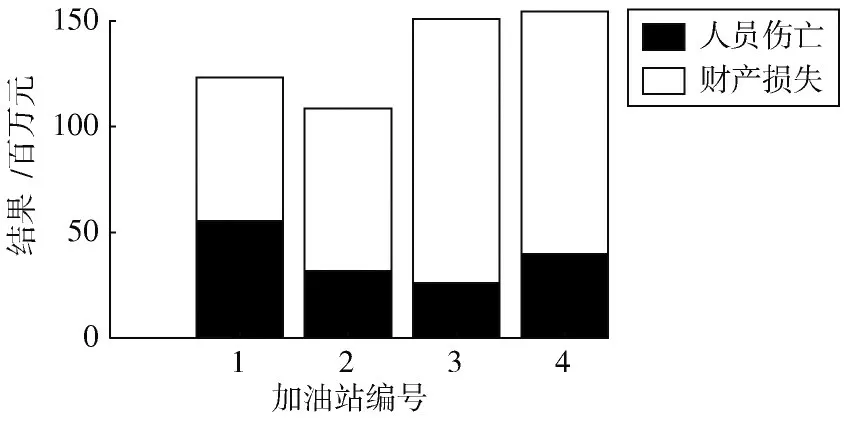
图3 加油站被成功攻击后的损失

3 实验结果及分析

3.1 完全信息博弈场景

图4 完全信息博弈模型获取的最优策略集

从图4a）可以看出，第4个加油站拥有最大的损失却没有防御资源，而第2 个加油站拥有最小的损失却几乎拥有所有防御资源。这就表明在完全信息博弈场景下，防守者不一定会向产生巨大后果的加油站调配额外的防御资源。另外，从攻击者角度考虑目标加油站的价值见图4，从攻击者类型为（图2）的角度来看，第1个加油站和第2 个加油站拥有更高的价值，因此分配了更多的防御资源；从攻击者角度来看，具有很低价值的第3 个和第4 个加油站分配一点防御资源、不分配防御资源。这就表明，在完全信息博弈场景下，从攻击者的角度来看，通常具有较高价值的加油站优先获得更多的防御资源。

3.2 贝叶斯博弈场景

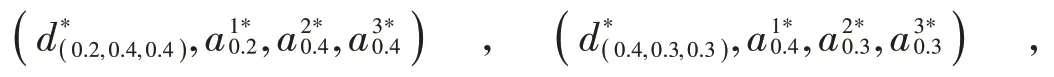
3.3 两种博弈场景对比分析

通过图4 和图5 的对比，实验表明处于贝叶斯博弈场景下的最优安全资源配置与在完全信息博弈场景下的最优安全资源配置有着极大的不同。以第4 个加油站为例，完全信息博弈场景下只有一种攻击类型的防御资源为0 单位，而贝叶斯博弈场景下有三种攻击者类型、和（0.2，0.4，0.4）的防御资源为42 单位。进一步对实验结果进行分析，当某一种类型攻击者的先验概率增加时，目前的方法能够帮助防守者修改防御资源配置来抵御该类型攻击者的攻击。

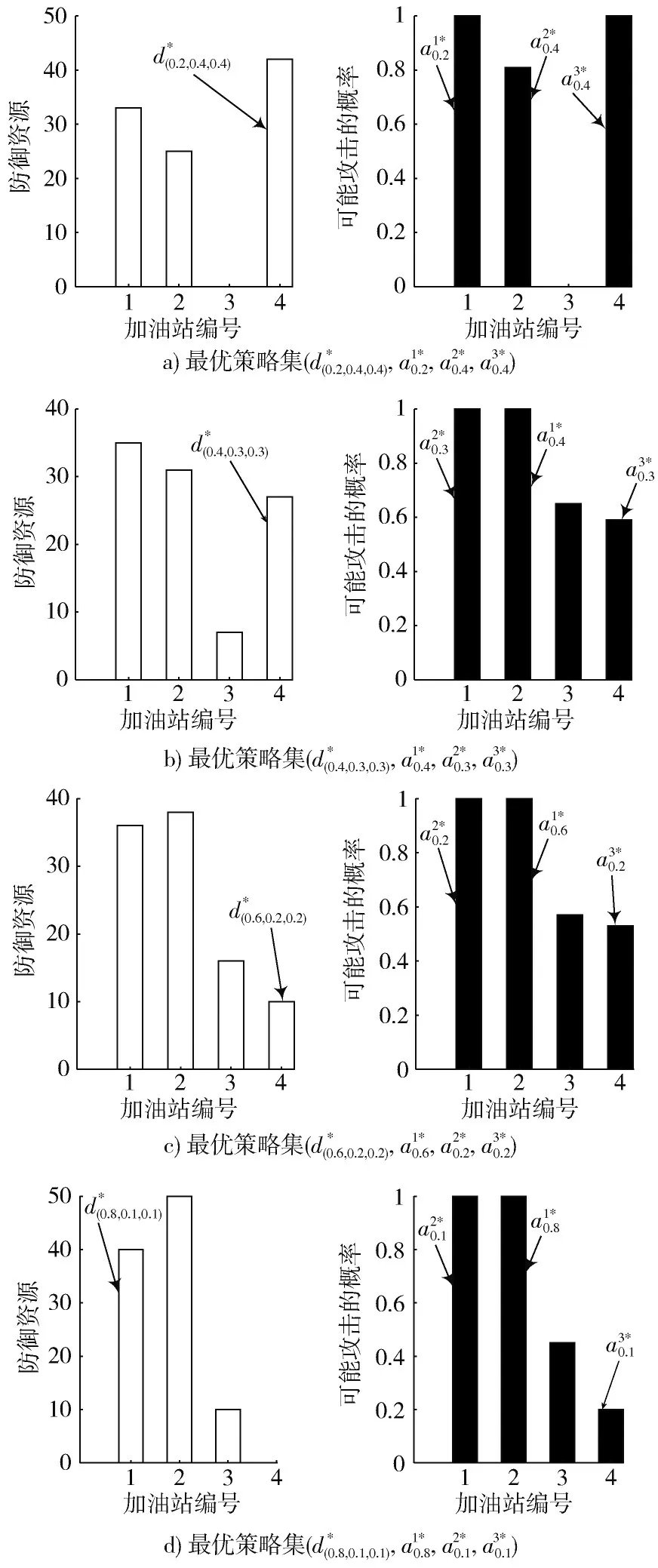
图5 贝叶斯博弈模型获取的最优策略集

如图6 所示，当存在多种类型的攻击者时，处于贝叶斯均衡下防守者的预期损失随着攻击者A的先验概率的增加而接近于纳什均衡（仅攻击者A），其中=100 单位，=0.015。

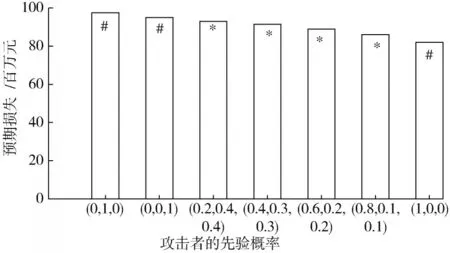
图6 纳什均衡（#）和贝叶斯均衡（*）下的预期损失

随着关键参数防御系数从0.005 增加到0.025，可用的防御资源被重新分配给更多的加油站，同时这也进一步降低了防守者的预期损失，如图7 所示。图7 中，=100 单位。在防御资源总量不变的情况下，通过增加贝叶斯博弈模型中的防御系数，防守者可以重新分配可用的防御资源，进一步降低预期损失。

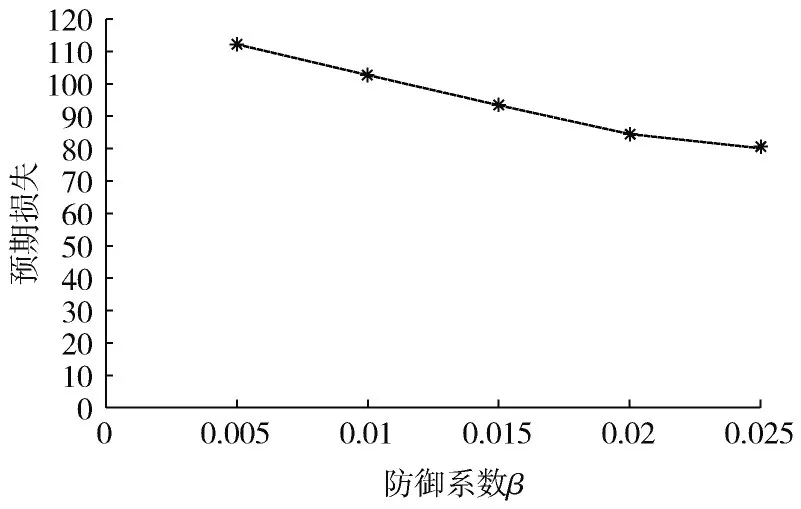
图7 不同防御系数下的预期损失

4 结 语

本文提出了一种基于贝叶斯博弈论方法的防御资源的分配策略，以保护加油站设施免受多种类型的攻击。通常情况下，对防守者而言，攻击者的类型无法确定，这使得防守资源的优化配置更加复杂和困难。为此本文引入了“先验概率”来量化特定类型的攻击者发起攻击的概率，使用先验概率分布来描述每种类型的攻击者发起攻击的可能性，并假设防守者知道每个加油站对不同类型攻击者的价值。对比分析实验结果得出，与完全信息博弈相比，贝叶斯博弈模型场景不仅能够更加合理地调配有限的防御资源，最大化减小预期损失，同时当某一种类型攻击者的先验概率增加时，目前的方法也能够帮助防守者修改防御资源配置来抵御该类型攻击者的攻击。当前本市公共安全部门十分重视基础公共安全设施的安保防护措施，投入了大量的人力、物力和财力，本文提供的模型以及方法可以在一定程度上更好地保护公共基础设施，为安全部门提供一些新的技术和策略参考。