融合分数阶和蝴蝶优化的改进粒子滤波算法
2022-05-10姜雨汐
刘 慧,姜雨汐
(北京建筑大学 电气与信息工程学院,北京 102612)
1 引 言
1999年Carpenter[1]等人首次提出粒子滤波器的概念.粒子滤波算法(Particle Filter,PF)是一种基于蒙特卡罗思想的非线性非高斯状态估计滤波方法[2],具有处理非线性、非高斯分布和多模态问题的能力[3],适用于移动机器人的定位滤波.PF算法是通过一组粒子来表示后验概率,但存在粒子退化和多样性丧失问题,严重影响粒子滤波的精度.为解决这一问题,Wang等人[4]提出一种最大似然粒子滤波算法(Maximum Likelihood Particle Filtering,MLPF),将传统粒子滤波器的预测和更新步合并为一步.与传统粒子滤波算法相比,MLPF算法以更少的粒子数量实现了更高的室内定位精度.也有一些学者将自然启发式算法与粒子滤波算法相融合,来解决滤波精度和运算效率的问题.崔昊杨等[5]提出一种改进粒子滤波方法,结合改进萤火虫算法(Firefly Algorithm,FA)提高了滤波精度和算法收敛速度.滕飞[6]等人针对计算效率低和计算精度下降的问题,提出一种基于KLD(Kullback Leibler distance,KLD)和蝙蝠算法的改进粒子滤波算法,能很好地提高计算精度和运算效率.Arora S和Singh S[7]提出一种蝴蝶优化算法(Butterfly Optimization Algorithm,BOA),这是一种基于蝴蝶觅食行为的全局优化算法,该算法具有更高的收敛性,优于其他自然启发式算法,如萤火虫算法[8]、蚁群算法[9]、人工蜂群[10]、蝙蝠算法等[11].刘云涛[12]提出基于蝴蝶优化的粒子滤波算法,在采样过程中引入蝴蝶优化算法,有效的改善了粒子退化问题.
分数阶(Fractional Order,FO)微积分有着300多年的历史,但是仅作为纯粹的数学概念被提出[13].分数阶模型与整数阶模型相比能表现出更好的性能,而且可以解决生活中整数阶系统无法解决的物理问题[14].近几十年来,越来越多的学者对分数阶的进行了深入研究,在系统的状态估计取得了很多成果.Mousavi等人[13]提出一种分数阶萤火虫算法(FO-FFA).采用FO微积分来解决萤火虫行为的记忆问题,提高了萤火虫算法的效率和鲁棒性.孙永辉等人[14]提出一种改进分数阶卡尔曼滤波,与传统的卡尔曼滤波相比,改进的算法对非高斯Lévy噪声滤波效果更好.赵亚亚等人[15]提出一种基于蚁群算法的分数阶随机状态最优估计,与经典蚁群算法状态估计相比,分数阶系统状态估计的精度更高.
本文针传统粒子滤波算法存在的粒子退化和多样性丧失问题,提出一种融合分数阶和蝴蝶优化算法的改进粒子滤波算法(BOA-FPF).引入蝴蝶优化算法,对粒子进行迭代寻优,不对其进行舍弃,能很好地解决粒子退化问题;在粒子更新过程引入分数阶,根据分数阶的历史记忆特性增加粒子多样性,从而解决粒子多样性丧失问题;在全局搜索和局部搜索时引入Lévy飞行,避免出现局部最优.最后,将改进算法与经典粒子滤波算法(PF)、融合蝴蝶优化的粒子滤波算法(BOA-PF)在不同的粒子数下进行仿真对比研究,说明改进算法的正确性和有效性.
2 算法原理
2.1 粒子滤波算法
粒子滤波算法(Particle Filter,PF)的基本思想基于蒙特卡罗方法,可用于移动机器人定位滤波.具体用于移动机器人定位的粒子滤波算法有:常规粒子滤波算法[16],自然启发式粒子滤波算法[17,18].自然启发式粒子滤波算法解决了粒子退化和多样性匮乏问题,这里主要针对融合蝴蝶优化的粒子滤波算法进行研究.
粒子滤波的核心思想是通过一组带有权重的随机样本对概率密度函数进行近似,通过不断调整粒子的权重和位置,从而估计系统状态,这些样本即称为“粒子”.
非线性系统的状态模型和观测模型的一般形式如下:
(1)
其中,f(·)和h(·)分别表示状态方程和观测方程,xt表示t粒子状态,ut表示控制量,wt和vt为噪声.
1)预测过程.
(2)
其中p(xt|z1:t-1)为t-1时刻观测值的t时刻的先验概率密度;p(xt|xt-1)为状态转移概率密度;p(xt-1|z1:t-1)为t-1时刻系统的概率密度.
2)状态更新.利用t时刻观测值zt更新p(xt|z1:t-1),t时刻系统后验概率密度为p(xt|z1:t).
(3)
其中:
(4)
粒子滤波基于序贯蒙特卡洛采样的思想,从后验概率密度p(xt|z1:t)采样近似后验分布.
(5)

3)计算各粒子权重.
(6)

4)归一化权重.
(7)
5)滤波.计算t时刻系统后验概率密度为p(xt|z1:t).
(8)
2.2 蝴蝶优化算法
蝴蝶优化算法(Butterfly Optimization Algorithm,BOA)[7,19]是以蝴蝶种群觅食行为作为启发的全局寻找最优解算法.在自然界中,蝴蝶群体内部的每一只蝴蝶在觅食时,自身既可以分泌一定强度的气味,也可以感受其它蝴蝶分泌的气味,并飞向那些散发更强气味的蝴蝶.蝴蝶分泌气味的强度由感知形态、刺激强度以及幂指数决定.用方程表示为[20]:
F=cIa
(9)
其中,F表示气味强度大小,c表示感知形态,I表示刺激强度,a表示幂指数.
BOA的基本步骤如下:
1)蝴蝶种群初始化.设定种群由n只蝴蝶组成,每只蝴蝶xi对应的刺激强度Ii由目标函数f(xi)决定;
2)寻找位置最优的蝴蝶.适应值Yi中的最大值决定了最优位置.计算蝴蝶的适应值Yi方程定义为:
(10)
式中R为观测噪声的方差;Znew为最新观测值;Zpred为预测的观测值;
3)确定搜索方式.首先根据式(9)计算蝴蝶散发的气味强度F.考虑到外界环境噪声的干扰,由随机数r决定使用局部搜索或全局搜索,以更新蝴蝶位置.全局搜索可以表示为:

(11)
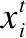
(12)
局部搜索可以表示为:

(13)
其中xi,xj,xk分别是第i,第j,第k个蝴蝶的空间位置.
为避免蝴蝶移动陷入局部最优,在算法中常常引入随机游走.随机游走是指式(13)中xj和xk从同一子群中随机选取.Lévy飞行是一种常用的随机游走方式,能够提高局部搜索效率,其游走公式如下[21]:
Lévy(λ)~u=t-λ,(1<λ≤3)
(14)
2.3 分数阶
2.3.1 分数阶系统
分数阶微积分是整数阶微积分的推广[13].基于分数阶微积分,分数阶系统具有历史记忆特性.历史记忆特性是非马尔可夫性的,从时域的角度描述了分数阶系统对历史过程的记忆能力.因为分数阶系统包含处理过的无限个项,因此分数阶系统对之前的所有事件有记忆[22].
定义1[14].Grunwald-Letnikov(GL)分数阶微积分定义为:
(15)
(16)

(17)
其中Dα[x(t)]是GL的α阶导数,Γ(·)是Gamma函数.α>0时为分数阶微分;α<0时为分数阶积分.h为步长,j为采样时刻.
在离散时间中,x(t)的分数阶微积分(GL)可定义为:
(18)
(19)
其中T为采样周期,r为采样时刻,也被称为截断阶次.
定义2[23]. 分数阶的差分方程为:
(20)
由式(20)可以看出,xk与之前的状态都相关,故离散分数阶系统是非马尔科夫性的,这也就是分数阶系统的历史记忆性.
2.3.2 分数阶粒子滤波算法
离散非线性分数阶系统可表示为:
(21)
其中∇是微分算子,k为采样时刻,xk为系统状态,α为差分阶次,zk为实际测量,xk∈n,α∈n,zk∈m,ωk∈n为系统噪声,vk∈m为测量噪声;

(22)
综上所述,FPF与经典PF不同之处在于,FPF是非马尔可夫性的,而经典PF是假设系统的状态转移服从一阶马尔可夫性的.即经典PF当前粒子状态仅与前一时刻粒子状态有关,而FPF当前粒子状态与之前所有的粒子状态有关.
通过式(16)、式(19)和式(20)可以看出,历史粒子状态随着时间的推移,对当前粒子状态影响逐渐减小,但却占用着很大的运算量,因此截断阶次r的选取影响着运算效率.
3 算法改进
3.1 融合蝴蝶优化的粒子滤波算法


(23)
3.2 改进粒子滤波算法
文结合分数阶和蝴蝶优化算法的思想,提出一种改进的粒子滤波算法.改进算法的实现过程如下:
2)预测.引入分数阶根据式(1)计算t+1时刻粒子预测值.
3)寻找最优值.根据PF和BOA的相似之处,PF中的一个粒子可以类比成BOA中的一只蝴蝶.每一个粒子的适应值由式(10)计算获得,全局最优的粒子g*由式(12)计算获得.
4)确定搜索方式.首先利用式(9)计算每一个粒子的气味Fi,然后利用切换值p和产生的随机数,来对粒子进行全局搜索(依据式(23))或局部搜索(依据式(13))加以判断.
5)粒子的重要性权重更新,并进行归一化操作.
6)重采样及状态输出.
图1为改进算法的流程图.
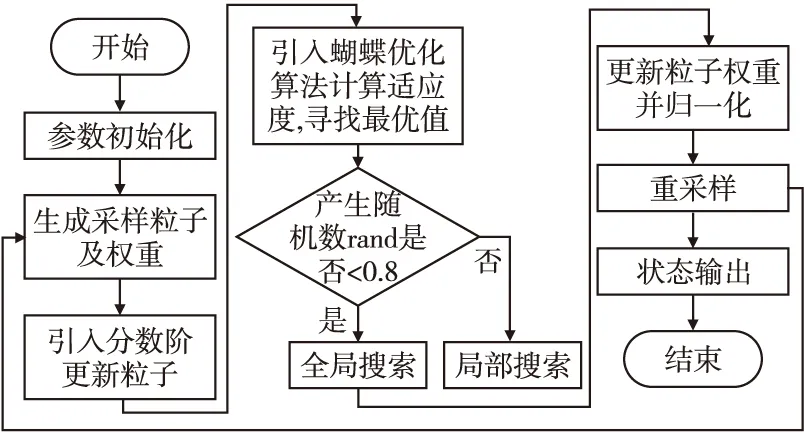
图1 改进算法流程图Fig.1 Improved algorithm flow chart
融合分数阶与蝴蝶优化的改进粒子滤波算法伪代码如算法1所示.
算法1.融合分数阶与蝴蝶优化粒子滤波
1.初始化参数:N、T、Q、R、c、a、p
2.更新:
Fork=1:T
生成采样粒子及权重
Fori=1:N
计算I(i)、F(i)、Y(i)
end
寻找最优值g*
Fori=1:N
产生随机数,判断全局搜索还是局部搜索
end
3.更新权重并归一化
4.重采样
End
4 实验结果及分析
4.1 仿真结果计分析
实验硬件环境采用CPU为Intel Core i7 处理器,内存16GB;软件环境为MATLAB 2014a.将经典粒子滤波算法(PF)、融合蝴蝶优化的粒子滤波算法(BOA-PF)以及融合分数阶与蝴蝶优化的改进粒子滤波算法(BOA-FPF),在粒子数目为50、100、150时进行对比和分析.系统状态方程和观测方程为[8]:
(24)
式(24)为典型的非线性、非高斯系统模型.算法中w(t)和v(t)为均匀分布的高斯白噪声.在比较研究中采用均方根误差ERMSE作为衡量各滤波算法的性能指标.均方根误差ERMSE为:
(25)
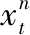
关于截断阶次r的选取,根据式(16)和式(18)可以看出,r越大分母j越大,历史粒子对整体的影响越小,但运算时间越长.表1统计了当粒子数N=50,截断阶次分别为r=3,4,8,12时运行时间和估计误差的结果.通过表1数据可以得出这样的结论:r取值越小运行时间越短,误差越大;r取值越大运行时间越长,但误差越小.因此,根据运行时间和误差的折中,在后续实验中截断阶次确定为r=4,也就是前4项微分即可.
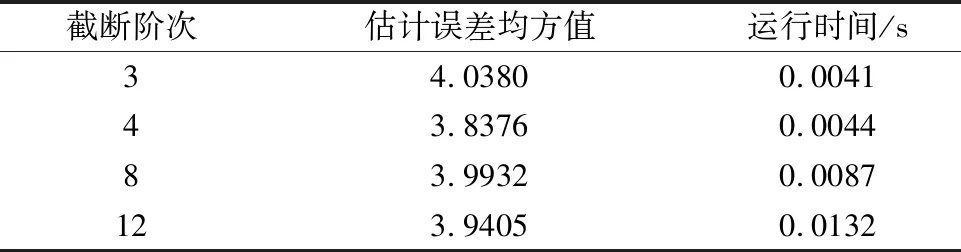
表1 不同截断阶次均方根误差和运行时间比较Table 1 Comparison of root-mean-square error and running time for different truncation orders
图2给出了粒子数为150时,上述算法的一阶状态估计仿真结果;图3给出了粒子数为150时,上述算法的一阶系统状态估计误差;表2给出了上述算法在粒子数为50、100、150时的均方根误差统计结果及其运行时间.

图2 一阶系统状态估计(N=150)Fig.2 First-order system state estimation(N=150)
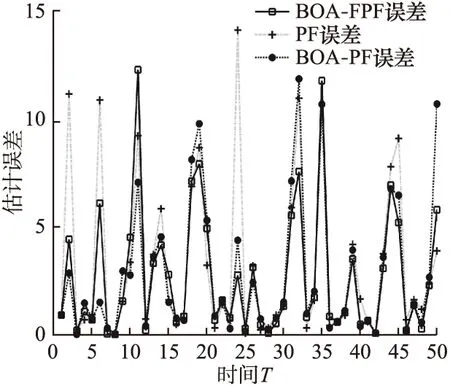
图3 一阶系统估计误差(N=150)Fig.3 First-order system estimation error(N=150)
从仿真结果可以看出,在粒子数为150的情况下,整体来看BOA-FPF的滤波误差相对较小,滤波表现相对稳定,很少出现偏差较大的情况.而PF和BOA-PF的滤波误差比BOA-FPF都大.通过表2的误差均方值可以看出,当粒子数较少,即N=50时,BOA-FPF的滤波误差保持在很小的状态,PF与BOA-PF均有出现误差较差的情况.随着粒子数的增多,当N=100时,PF的滤波误差有着明显的增大,BOA-PF与BOA-FPF的滤波误差都比较小.当N=150时,也就是在粒子数较多的情况下,3种算法均出现不同程度的波动,但BOA-FPF表现最为稳定,滤波效果最好.

表2 一阶均方根误差和运行时间比较Table 2 Comparison of first-order root mean square error and running time
通过表2的运算时间可以看出,PF的运算时间最短,BOA-FPF在3种算法里运算时间较长,这是由于BOA-PF与BOA-FPF是在经典PF基础上发展而来,为了提高精度而增加了计算量,因此时间成本比PF略高,根据仿真数据可以看出,BOA-FPF以牺牲时间代价获取高精度,该时间代价仍然可以满足系统要求.
4.2 仿真应用
本文还针对二阶非线性系统进行仿真应用研究,采用的二阶非线性状态方程和观测方程为:
(26)

图4给出了PF、BOA-PF以及BOA-FPF算法的轨迹仿真结果,图5给出了这几种算法所对应的误差,表3给出了它们的均方根误差统计结果及其运行时间.

图4 二阶系统状态估计(N=20)Fig.4 Second-order system state estimation(N=20)
从图5以及表3可以看出,虽然PF算法运行时间最短但是误差在3种算法里最大.从图4可以看出BOA-PF出现局部与真实轨迹偏差较大的情况.上述结果表明,相较于PF与BOA-PF,BOA-FPF与真实轨迹偏差最小,误差最小,虽然运行时间较长,但是在系统响应时间内,具有一定的实用价值.

图5 二阶系统估计误差(N=20)Fig.5 Second-order system estimation error(N=20)
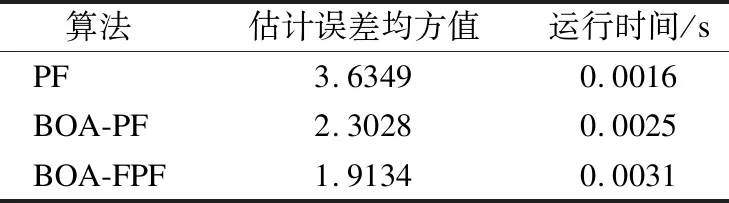
表3 二阶均方根误差和运行时间比较Table 3 Comparison of second-order root mean square error and running time
5 结 论
本文针对传统粒子滤波算法造成的粒子退化和多样性丧失问题,提出一种融合分数阶和蝴蝶优化的改进粒子滤波算法.该算法引入分数阶保留了粒子多样性,结合Lévy飞行的蝴蝶优化算法,避免局部最优.通过对本文提出的算法BOA-FPF与融合蝴蝶优化的粒子滤波算法BOA-PF、经典粒子滤波算法PF进行仿真对比研究,得到以下结论:改进算法BOA-FPF发挥了粒子多样性的优势,减少粒子退化,避免了局部最优,与PF、BOA-PF相比,滤波精度提高.由于算法以提高精度为主要目标,计算时间略长,经过系统仿真和测试,该时间代价仍然可以满足系统要求.因此,该算法对实际室内移动机器人的定位系统应用具有一定的指导意义.
