离散属性的朴素贝叶斯分类算法的优化
2022-05-10李福祥王建敏梁建创
李福祥,王建敏,梁建创,2,王 雪
1(哈尔滨理工大学 理学院,哈尔滨 150080)
2(钜泉光电科技(上海)股份有限公司 技术研发部,上海 200000)
1 引 言
当今社会高速发展,高新技术遍地开花,万物之间的联系使得信息量急剧增加,各领域对海量数据的分类处理的需求也增多,因此对分类技术的研究也一直是众多学者关注的重点.贝叶斯分类器其核心就是贝叶斯定理,在其分类过程中运用了概率统计的知识而塑造的一类算法.其中,朴素贝叶斯分类器(Naive Bayes Classifier,NBC)对贝叶斯分类器进行了理想化和简化,成为最经典的分类算法,与其他分类算法相比,具有很大的优势,NBC之所以简单是因为它引入了一个很强的限制条件:属性条件独立性假设,凡事有利就有弊,虽然降低了计算开销,但却损失了算法分类精度,现实生活中数据是复杂的,真正的独立是很少的,所以这个条件在实际生活中是很难成立的.为了提高算法分类性能,人们自然会想到探索属性之间的依赖关系,借助其他算法改进朴素贝叶斯分类器,降低不切实际的独立性假设带来的影响.FRIEDMAN选择从结构上改进朴素贝叶斯分类器,构造了TAN算法[1],以最大带权生成树算法[2]为基础,将无序分类变为有序分类.金哲将遗传算法引入到了NBC中,在此基础之上提出了GBAN分类器[3].眭俊明等人利用高阶频繁项集的原理,充分考虑了数据属性间的相关性,从而提出了新的贝叶斯分类算法:FISC算法[4].王中锋等人通过对TAN分类器结构的分析,提出一种不考虑边重定向的TAN分类器[5].ZHOU通过分析贝叶斯分类原理和改进方法,利用粗糙集对属性进行约简,提出了一种同时改进属性约简和权重的朴素贝叶斯算法[6].宁可等人为了对高维连续数据离散化,采用了高斯分割的方法,提出了基于属性关联的朴素贝叶斯分类算法[7],属性数量越多,算法分类效果提升越明显.张坤等人提出了一种利用可分解的评分函数构建TAN分类器的算法[8].余良俊等人用MI衡量不同属性对分类的贡献度,利用ODE模型分类器进行判别,提出MI-ODE算法[9].
对于分类算法而言,数据的属性一般划分为两种:连续型和离散型,连续属性也称为定量属性,例如:人的身高体重、西瓜的含糖率和密度等.离散属性也称为定性属性,例如:颜色、性别等.对于连续属性的取值允许被排序,也能进行各种算术运算,几乎都可以被学习器所用,如有必要,可以视具体问题而定,进行对应的预处理分析.离散属性具有有序和无序之分,有序离散属性是指各类别之间有程度的差别,例如:成绩属性的取值可以分为优、良、中、及格、不及格,无序离散属性是指所分类别或属性之间无程度和顺序的差别,例如:性别属性的取值可以是男、女,离散属性虽然可以很好的描述属性的性质,但是无法进行算术运算.
大部分的分类模型都是基于数学运算,所以字串资料是无法运算的.基于此,本文对朴素贝叶斯分类器的离散属性进行数据预处理,采用数值标记[10]的方法将离散属性转换成连续的数值,即用指定的数来代表离散属性的取值,比如:对于头发颜色,我们规定1代表黑,2代表白,往后推.对离散属性做数据预处理之后,这样就可以对离散属性进行数值计算.
朴素贝叶斯分类器的假设在现实中往往不能满足,使得分类精度降低.针对这个问题,本文通过正交矩阵对连续属性和数值标记的离散属性做正交变换,变换之后的属性特征消除了属性之间线性关系的影响,增强了属性的条件独立性,贴近了NBC的假设条件,从而提高算法分类精度.将改进后的算法用典型数据测试、分析,与朴素贝叶斯(NBC)、贝叶斯网(BN)相比,改进的算法(INB)分类性能提高.
2 朴素贝叶斯分类器简介
朴素贝叶斯分类器[11]是基于贝叶斯定理和属性条件独立性的一种分类算法.设样本数据集D={x1,x2,…,xm},每个样本xi=(xi1,xi2,…,xin)是一个n维属性向量,类别标记为y={c1,c2,…,cN},即D可以分为N个类别.
基于贝叶斯定理,后验概率P(c|x)可表示为:
(1)
其中,P(c)是类“先验”概率;P(x|c)是样本x相对于标记c的类条件概率;P(x)是证据因子.
朴素贝叶斯基于属性条件独立性假设,对已知类别,上式可表示为:
(2)
其中n为属性数目,xi为x在第i个属性上的取值.
由于对所有类别来说P(x)相同,因此由贝叶斯判定准则有:
(3)
这就是朴素贝叶斯分类器的表达式.
3 相关定理
定理1.[12]分布函数序列{Fn(x)}弱收敛于分布函数F(x)的充要条件是{Fn(x)}的特征函数序列{φn(t)}收敛于F(x)的特征函数φ(t).
通常以上定理称为特征函数的连续性定理,因为它表明分布函数与特征函数的一一对应关系有连续性.
定理2.[12]设{Xn}是独立同分布的随机变量序列,且E(Xi)=μ,Var(Xi)=σ2>0存在,若记
则对任意实数y,有:

(4)

又因为E(Xn-μ)=0,Var(Xn-μ)=σ2,所以有:
φ′(0)=0,φ″(0)=-σ2
于是特征函数φ(t)有展开式:
从而有:
而e-t2/2正是N(0,1)分布的特征函数,定理得证.
上述定理只假设n独立同分布、方差存在,不管原来的分布是什么,只要n充分大,就可以用正态分布去逼近随机变量和的分布.
定理3.[13]实对称矩阵M的属于不同特征值的特征向量是正交的.
定理4.[13]实对称矩阵一定可以正交相似于对角矩阵.
4 数据预处理
4.1 缺失数据的处理
在现实生活中,由于多方面的原因,我们很难遇到完美的数据,要么无法直接获取想要的数据,要么就是获取到的数据不尽如人意,一旦拥有了高价值的数据,就能进行高效的数据挖掘,而在数据分析过程中,经常会遇到数据值缺失的问题,这也是难以避免的.对缺失值的处理方法有很多,主要是从删除元组、数据补齐、不处理这3个角度来处理缺失值[14].由于本文所采用的数据集缺失值比较少,所以对缺失数据的处理就根据统计学中的众数原理,用该属性在其他所有对象的取值次数最多的值(即出现频率最高的值)来补齐该缺失的属性值[15].
4.2 离散属性连续化处理
一般而言,数据的属性一般分为两种类型:一种是连续(定量)属性,通过连续的数值来刻画被研究对象的某些属性,如人的身高、体重等;另一种是离散(定性)属性,通过文字语言或少量离散数值来描述被研究对象的某些属性,如颜色、性别等.现实世界中,绝大多数的数据库中,既包含了连续属性,又包含了离散属性.
朴素贝叶斯分类器的思想基础就是对于给出的未分类对象,也就是测试集,计算在该测试集出现的条件下每个类别出现的概率,比较这些概率大小,将测试集判给概率最大的一类.也就是说,在类先验概率的基础上将数据集归为n个标签中后验概率最大的标签(基于最小错误率贝叶斯决策原则),NBC对于连续型样本属性的类条件概率计算公式使用概率密度函数估计,对于离散型样本属性的类条件概率计算公式根据频率估计概率得到.本文将离散型样本属性通过数值标记的方法将其连续化[16],处理之后的离散型样本属性的类条件概率计算公式也通过概率密度函数来估计.
设样本数据集D={x1,x2,…,xm},每个样本xi=(xi1,xi2,…,xin)是一个n维属性向量,属性Ak有nk个取值,先对数据集的属性值进行数值化预处理,把属性Ak的nk个可能的取值按1到nk进行数值标记[17],例如:将西瓜数据集中色泽:青绿、乌黑、浅白转化为1,2,3.类别标记为y={c1,c2,…,cN},即D可以分为N个类别.
通过数值标记就可以将离散型样本属性进行了数值化处理[18],这样就可以计算各类样本在各个属性上取值的均值和方差,就可以使用概率密度函数来估计离散型样本属性的类条件概率.
5 改进的朴素贝叶斯分类器(INB)
5.1 训练过程
设样本数据集D={x1,x2,…,xm},每个样本xi=(xi1,xi2,…,xin)是一个n维属性向量,属性Ak有nk个取值,类别标记为y={c1,c2,…,cN},即D可以分为N个类别,训练步骤如下:
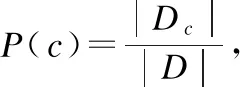
步骤2.补齐缺失值,根据统计学中的众数原理,用该属性在其他所有对象的取值次数最多的值(即出现频率最高的值)来补齐该缺失的属性值.
步骤3.对离散属性进行数值标记,把属性Ak的nk个可能的取值按1到nk进行数值标记,例如:将西瓜数据集中色泽:青绿、乌黑、浅白转化为1,2,3.

步骤5.计算正交矩阵P,使得PTMP=Λ,其中Λ为对角矩阵.计算M的全部特征值,并求出相应的特征向量,构造正交矩阵P.如果M的特征值有重根,可以通过施密特正交化过程,然后经过单位化,得到一个标准正交基,也就是正交矩阵P;如果M的全部特征值无重根,那么直接将特征向量单位化即可,同样得到正交矩阵P.

(5)
矩阵P可以将矩阵M相似对角化,乘积矩阵P-1MP的主对角元素是矩阵M的特征值:
通过上述方法所求的P是正交矩阵,可知P-1=PT,所以正交矩阵P可以将实对称矩阵M合同对角化,使得PTMP=Λ,其中Λ为对角矩阵.


步骤8.基于最小化分类错误率的贝叶斯判定准则对测试集进行分类.
5.2 实验结果及分析
首先对实验数据集进行描述,然后根据算法步骤设计实验,在对比试验中,从UCI数据库中选取9个数据集,用十折交叉的方法,检测本文提出的改进的朴素贝叶斯分类器(INB)、标准的朴素贝叶斯分类器(NBC)、贝叶斯网(BN)这3个分类器的分类性能.
将本文的改进的朴素贝叶斯分类器(INB)与朴素贝叶斯(NBC)、贝叶斯网(BN)进行比较.
5.2.1 数据描述
本文从UCI机器学习数据库中选取了9个数据集分别为balance、breast-cancer、car evaluation、German credit、hayes-roth、hepatitis、liver-disease、mushroom、tic-tac-toe,如表1所示.

表1 数据集描述
5.2.2 实验设计
为了验证本章提出的改进的朴素贝叶斯分类算法的有效性,对算法进行测试.实验环境如下:
1)硬件环境:1.5GHz CPU,内存为4GB,硬盘100GB以上的个人计算机.
2)软件环境:Windows 10 Professional 操作系统,用Python3.8编程实现.
本文采用十折交叉验证估计算法的准确性.十折交叉验证的步骤:先将数据集划分成10个大小相似的互斥子集,每个子集尽可能保持数据分布的一致性,轮流将其中9个子集的并集作为训练集,剩余的1个子集作为测试集,进行试验.每次试验都会得到相应的正确率,10次结果的正确率的平均值作为对算法精度的估计.原理如图1所示.
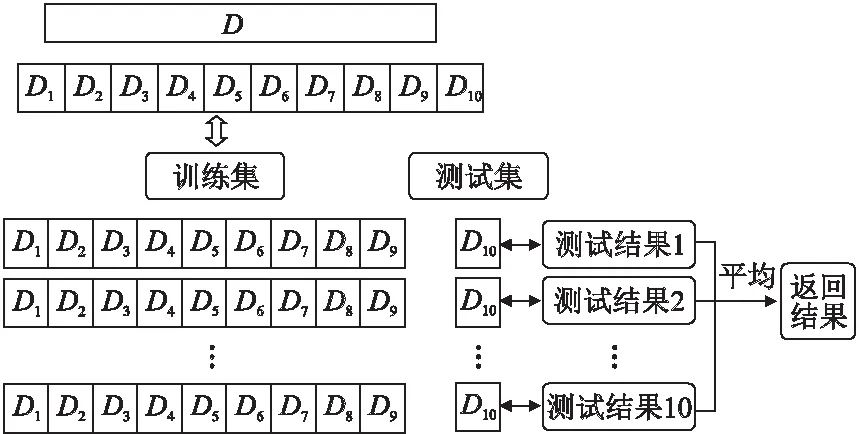
图1 十折交叉验证法原理图
分类任务中最常用的性能度量就是错误率和正确率.把分类错误的样本数占样本总数的比例称为错误率,即如果在m个样本中有a个样本分类错误,则错误率为:
则分类正确率为:
一般用百分比形式表示.本文采用正确率对分类算法进行性能评估.
5.2.3 实验结果
对所有数据集,采用十折交叉验证,分别记录标准朴素贝叶斯(NBC)、贝叶斯网(BN)和改进的朴素贝叶斯(INB)的分类正确率,最后将得到的结果进行比较,如表2、图2所示.

表2 各种算法的分类正确率

图2 NBC、BN和INB分类正确率对比
从表2、图2中可看出,改进的朴素贝叶斯分类器(INB)在本文中所使用的9个数据集分类准确率都优于朴素贝叶斯(NBC)、贝叶斯网(BN),运行时间和朴素贝叶斯分类器差别不明显,说明了改进的算法分类(INB)的有效性和准确性.
6 结 论
本文在朴素贝叶斯分类器的基础上,提出一种改进算法,详细介绍了改进算法的训练过程,对离散属性数值标记,之后用正交矩阵对连续属性和处理之后的离散属性做正交变换,增强了属性之间相互独立性,贴近了朴素贝叶斯分类器的属性条件独立性假设,从而提高了算法的分类准确率.最后通过UCI数据集对比改进的朴素贝叶斯分类(INB)、朴素贝叶斯(NBC)、贝叶斯网(BN)的分类正确率,实验结果表明,改进的朴素贝叶斯分类器(INB)的分类性能有较大的提高.
