一种适用于中压直流系统的电平多级倍增MMC拓扑及其调制策略
2022-05-09许同王琛陶建业王毅刘飞王世斌田旭刘联涛
许同,王琛,陶建业,王毅,刘飞,王世斌,田旭,刘联涛
(1. 新能源电力系统国家重点实验室(华北电力大学),河北省保定市 071003;2. 国网青海省电力公司经济技术研究院,西宁市 810008)
0 引 言
凭借高传输效率、高可控性以及便于接纳可再生能源等优势,中压直流系统已应用于贵州城市配电网、杭州江东新城智能柔性直流配电网、吴江中低压直流配电网等多项实际工程中[1-4]。模块化多电平换流器(modular multilevel converter,MMC)具备拓展性强、模块化设计、控制简单等优点,已成为中压柔性直流输电系统的优选换流器拓扑,并展现出良好的运行效果[5-6]。
相比于传统两电平和三电平换流器,MMC将电容分散在子模块内部,通过提高电平数目改善电压质量,同时降低器件开关频率[7-8]。调制策略是换流器正常工作的基础,直接影响换流器的运行性能[9-10]。最近电平逼近调制(nearest level modulation,NLM)采用多电平阶梯波逼近正弦参考波,应用于中压直流系统时,输出电压的低次谐波含量较高[11];采用载波移相脉宽调制(carrier phase shifted pulse width modulation,CPS-PWM)策略能够降低输出电压的低次谐波含量,但控制系统复杂,换流器运行损耗较高[12-13]。因此,亟需研究适用于中压直流系统的MMC拓扑及其调制策略,以改善换流器的运行性能。
通过改善传统NLM和CPS-PWM调制策略,国内外学者相继提出了多种适用于中压直流系统的新型MMC调制策略。文献[14]提出了载波重叠脉宽调制(phase disposition PWM,PD-PWM)策略,但该策略加剧了子模块电容电压不均衡度,且换流器控制系统复杂,运行损耗较高。文献[15-16]研究了特定谐波消除脉宽调制(selective harmonic elimination PWM,SHE-PWM)策略,通过傅里叶分解计算触发角,但计算方法过于复杂。文献[17]提出了等效电平调制策略(equivalent level modulation,ELM),该策略通过等效方波提高输出电平数目,简化了控制方法,但是低次谐波含量较高。文献[18-19]通过改进取整函数,将输出电压扩展至2N+1电平,改善输出电压波形质量,但也产生了较大的循环电流,换流器运行损耗较高。文献[20]提出了最近电平脉宽调制(nearest level PWM,NL-PWM)策略,该策略结合了阶梯波和PWM波,改善了输出电压的波形质量,电压均衡控制简单,但换流器的运行损耗较高。
针对应用于中压直流系统的MMC,已有调制策略虽然可以提高输出电压的波形质量,但是仍存在循环电流大、换流器运行损耗高、控制系统复杂等限制条件。为了提高应用于中压直流系统中MMC的运行性能,本文提出一种输出电平多级倍增MMC(level multiplication-MMC,LM-MMC)拓扑,并且设计相应的电平多级倍增调制(level multiplication modulation,LMM)策略。所提拓扑及其调制策略具有循环电流小、运行损耗低等优点,可多级倍增输出电平数目,从而改善输出波形质量。
本文首先介绍半桥MMC的拓扑结构,概述传统MMC调制策略的工作原理。其次,给出所提LM-MMC的拓扑结构,并且介绍B型子模块的工作原理。接着,设计LMM的调制原理以及子模块工作模式确定流程图。最终,分别搭建仿真和实验系统,验证所提拓扑及调制策略的运行特性,并与其他几种典型调制策略对比运行性能。
1 MMC运行原理及传统调制策略
1.1 MMC运行原理
图1为传统三相MMC的拓扑结构,每相单元包括上下2个桥臂,每个桥臂由N个半桥子模块(half bridge submodule,HBSM)和一个桥臂电感串联组成。
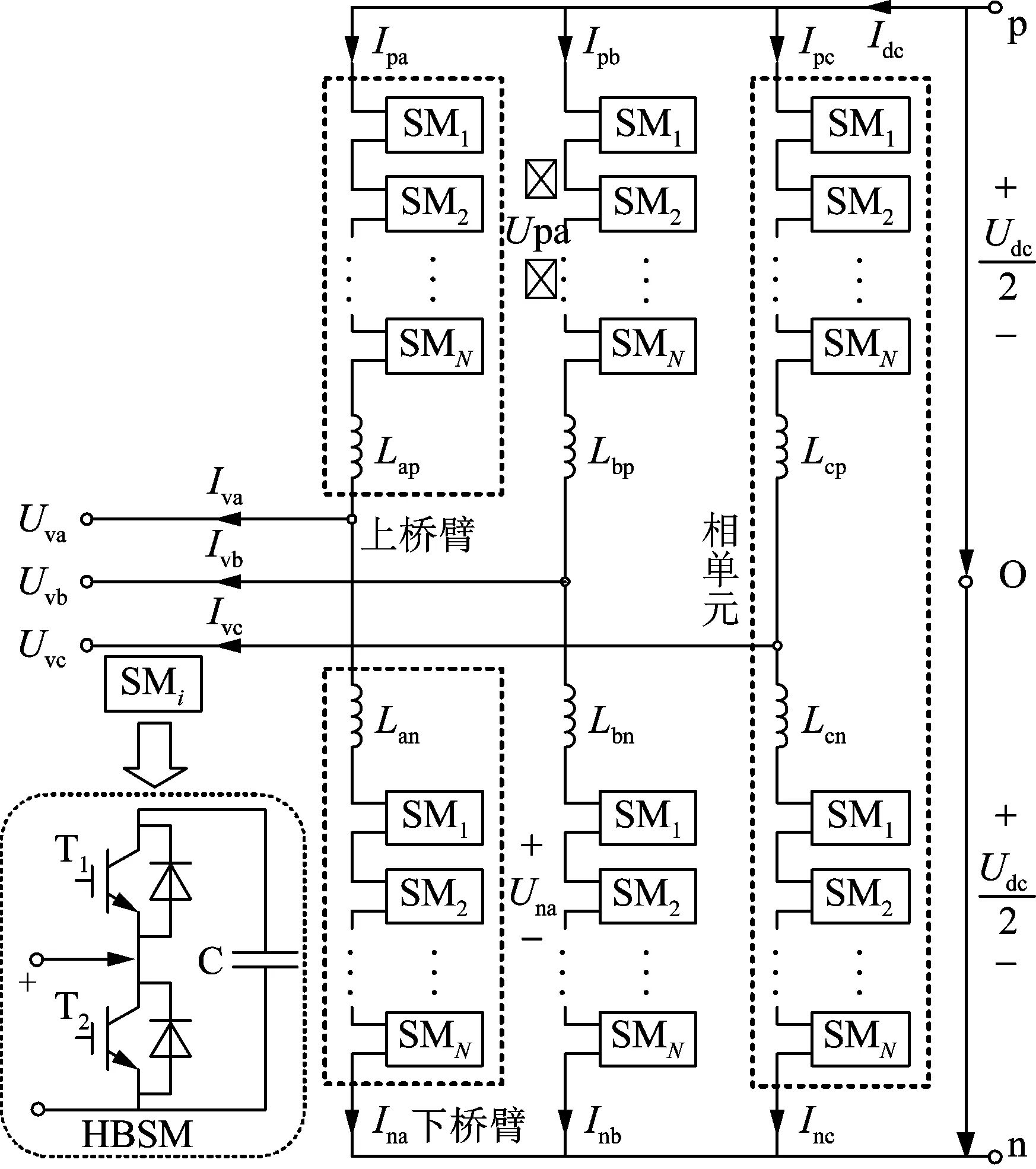
图1 传统三相MMC拓扑结构Fig.1 Topology of traditional three-phase MMC
如图1所示,Uvj和Ivj(j=a,b,c)分别为MMC交流电压和电流,Upj和Unj分别为上下桥臂的输出电压,Ipj和Inj分别为上下桥臂电流,Idc和Udc分别为直流电流与电压。在正常运行状态下,相单元上下桥臂投入子模块数目之和恒定,保证相单元输出电压稳定以减小循环电流。
(1)
1.2 传统调制策略
本节将简要概述实际工程中采用的NLM和CPS-PWM策略。
1.2.1 NLM策略
假设MMC各桥臂N个子模块电容电压额定值为Uc,换流器桥臂单元可输出N+1电平。图2为传统NLM原理,采用多电平阶梯波逼近正弦参考波,通过提高子模块数目改善输出波形质量。
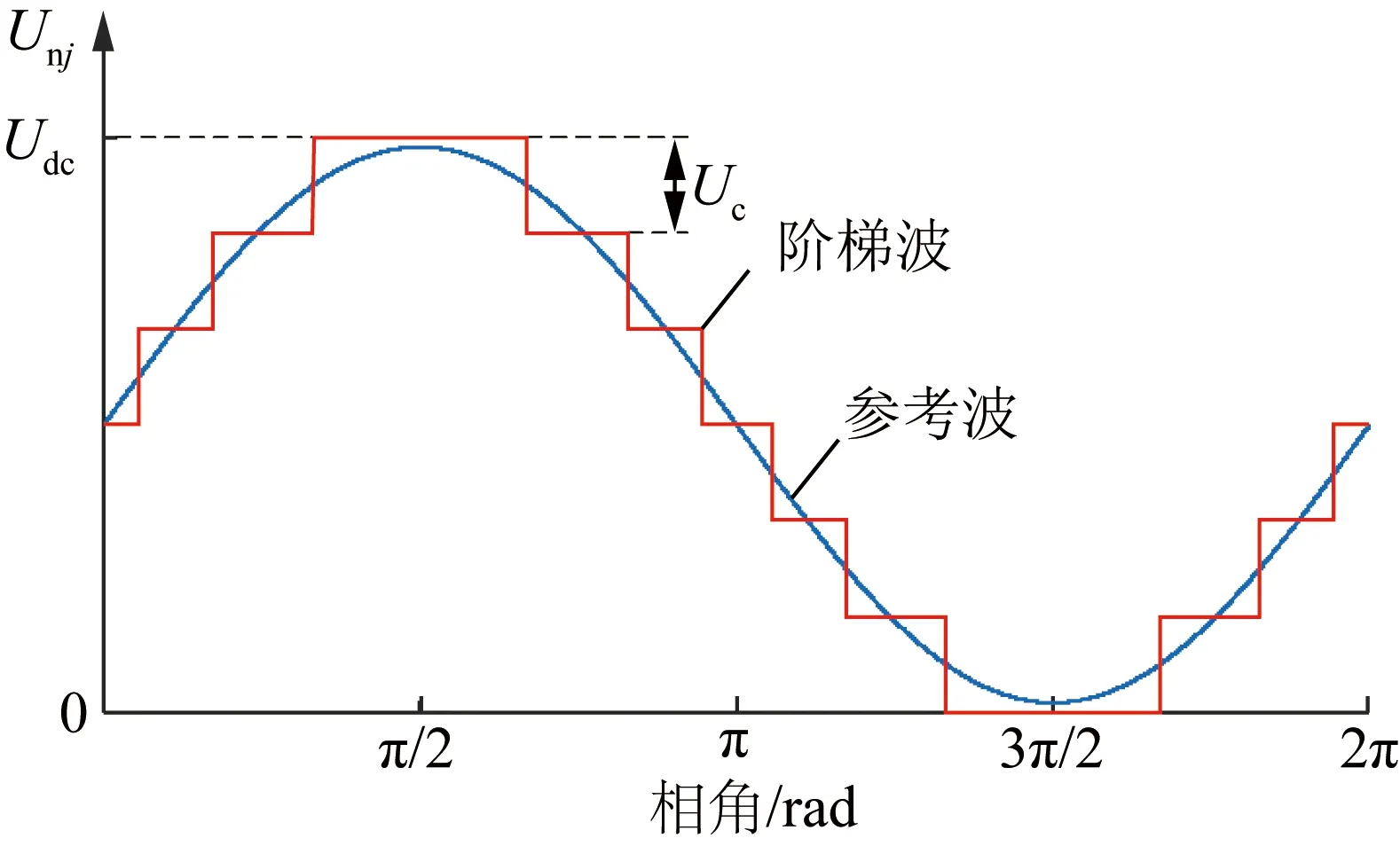
图2 传统NLM原理Fig.2 Schematic diagram of traditional NLM
由于感性器件可以滤除高次谐波,因此本文主要统计总谐波畸变度(total harmonic distortion,THD)和低次谐波畸变度(<1 000 Hz)(THDL)。在传统NLM调制下,相单元投入子模块数为N,输出N+1电平阶梯波。通过修改取整函数,可将相电压阶梯波电平数目扩展至2N+1[21]。然而,此时相单元投入子模块数目变化,引起较大的循环电流,换流器的运行损耗显著提高。此外,NLM一般在输出电平变化时排序电容电压以降低功率器件的开关频率,但是电压不均衡度也会因子模块数较少而增加。
1.2.2 CPS-PWM策略
图3所示为适用于中压系统中MMC的CPS-PWM原理。每个子模块分别对应一个三角载波,各三角载波互相差2π/N,将N个两电平PWM波叠加即可得到N+1电平PWM波。
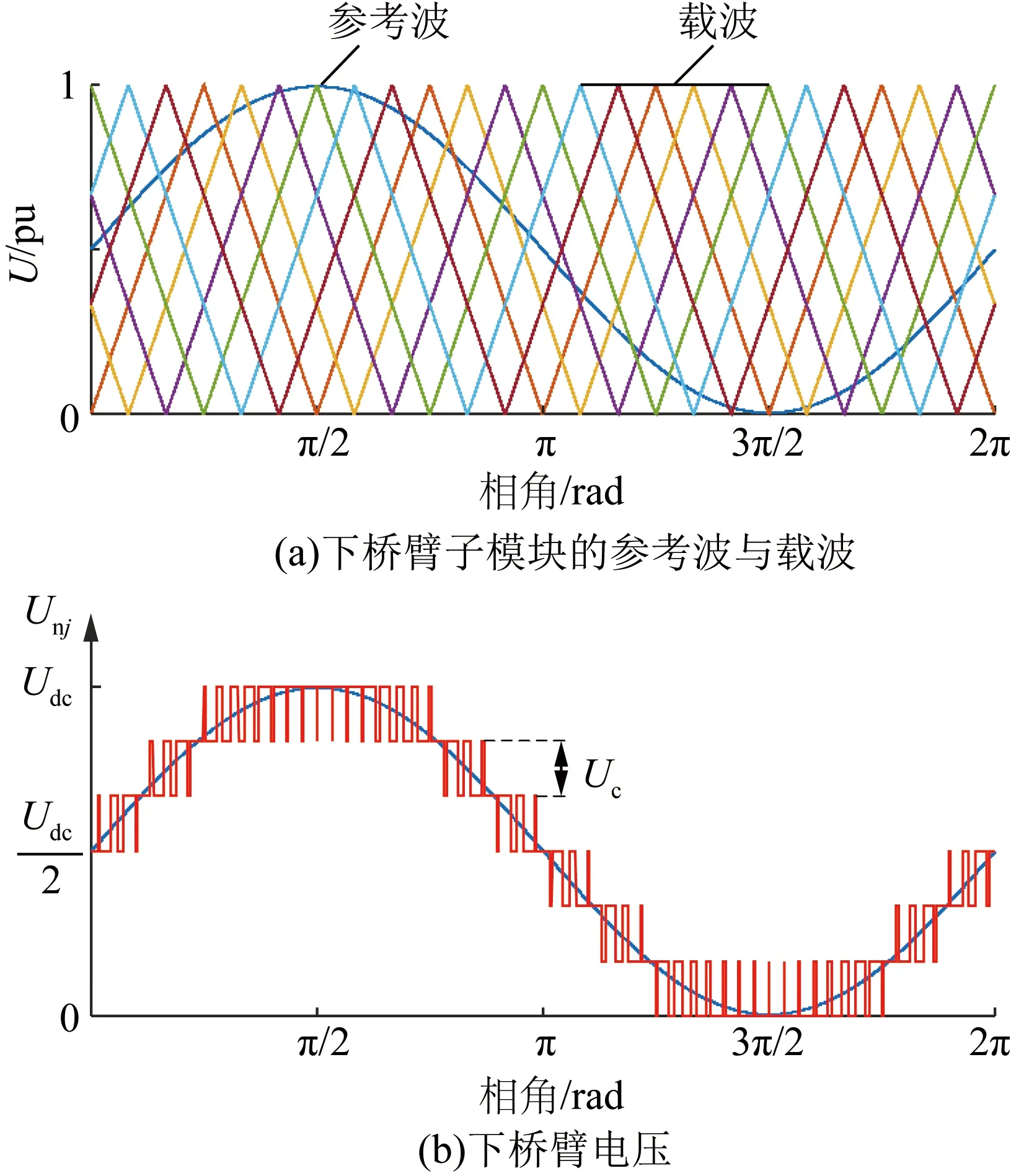
图3 CPS-PWM原理图Fig.3 Schematic diagram of CPS-PWM
在传统CPS-PWM方法下,上下桥臂对应子模块的三角载波相同,相单元投入的子模块数量之和为N,输出N+1电平。为了将输出电压扩展至2N+1电平,可将上下桥臂对应子模块的三角载波偏移半个周期,此时相单元投入子模块数变化,大幅增加换流器的循环电流和运行损耗[21]。为了提高输出电压的波形质量,三角载波的运行频率较高,导致换流器的运行损耗增加。此外,电容电压均衡则是通过在参考波上注入均衡信号,增加了控制系统的复杂度,降低了输出波形质量。
2 电平多级倍增MMC拓扑结构
2.1 MMC拓扑结构
为了提高输出电平数量,改善输出波形质量,本文设计了LM-MMC拓扑,如图4所示。LM-MMC拓扑中,各桥臂由p个A型子模块与d个B型子模块串联组成。A型子模块为HBSM,电容值为C,电容电压为Uc,可输出0或Uc。B型子模块包括d个电容,每个电容值为dC,电容电压为Uc/d,可输出0、Uc/d或Uc。当d个B型子模块配合时,即可将输出电压的电平数目近似扩大d倍。
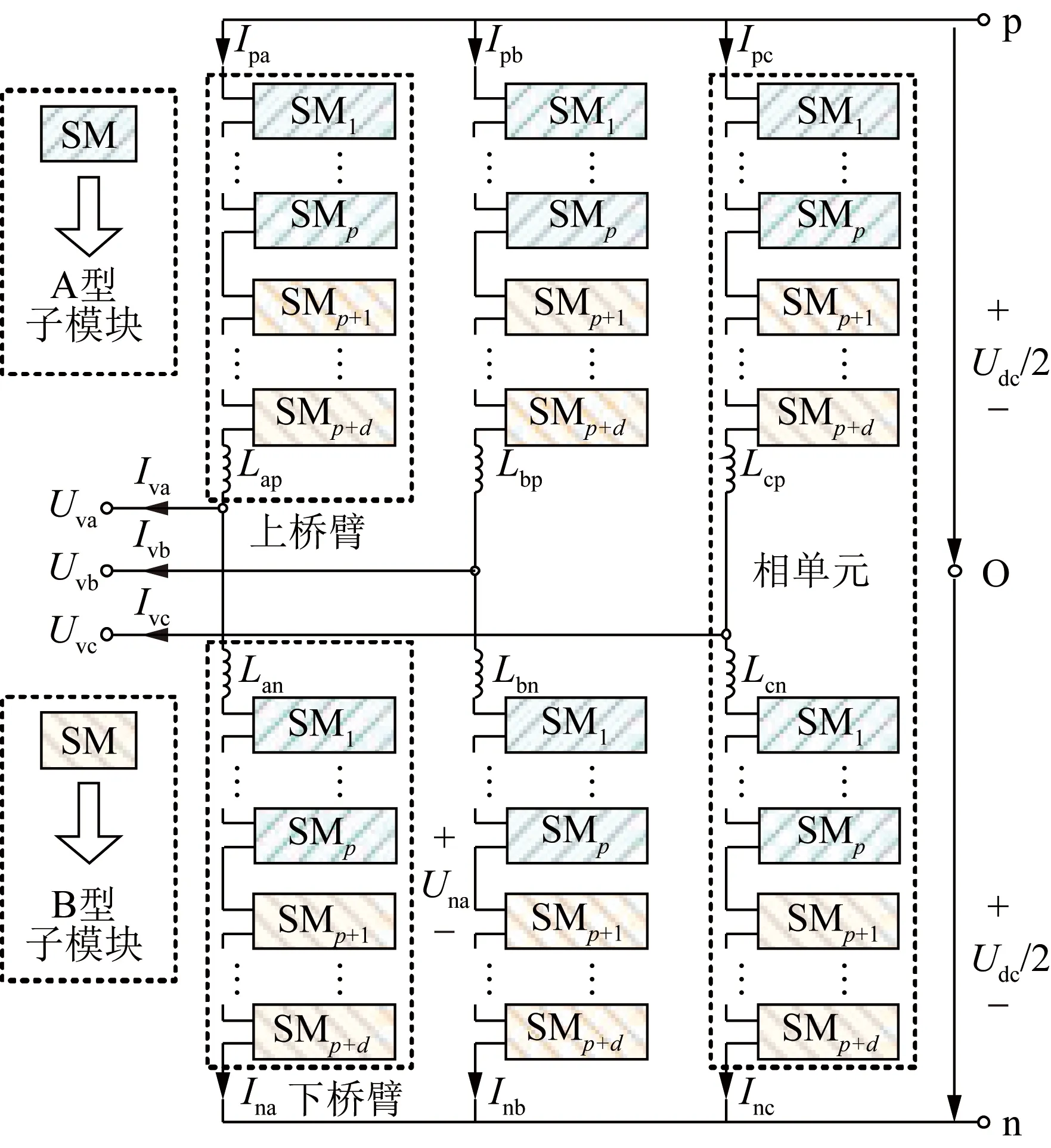
图4 电平多级倍增MMC拓扑结构Fig.4 Topology of LM-MMC
在本文所提LM-MMC中,通过引入B型子模块输出非整数电平,增加输出电平数。当桥臂单元输出电平为Uc的整数倍时,此时不需要输出非整数电平,经排序后确定A型与B型子模块工作模式,子模块输出电压为0或Uc;当桥臂单元输出电平为Uc的非整数倍时,此时需要输出非整数电平,因此优先确定B型子模块以提供非整数电平,将剩余子模块经排序后确定工作模式,子模块输出电压为0或Uc。
2.2 B型子模块的拓扑结构
根据上述分析可知,B型子模块提供非整数电平实现交流输出电平倍增,改善波形质量。为了减小B型子模块内部电容之间的电压偏差,电容的工作状态相同,子模块输出电压为0、Uc/d、Uc。由d个电压为Uc/d的电容旁路输出0,并联输出Uc/d,串联输出Uc,电容电压偏差较小,并联输出时所产生的暂态电流得以降低。由于B型子模块需要具备并联输出能力,通过查阅文献发现,可采用双半桥子模块(double half bridge submodule,D-HBSM)构成[22]。当d为2时,一个D-HBSM即可构成B型子模块,如图5所示;当d为3时,则需要2个D-HBSM以并联方式构成B型子模块,如图6所示。
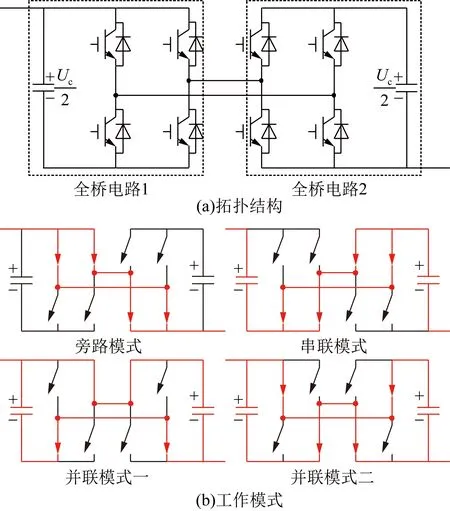
图5 B型子模块的拓扑结构及工作模式(d=2)Fig.5 Topology and working model of B-SM(d=2)
图5(a)为d取2时B型子模块的拓扑结构,图5(b)为B型子模块的工作模式。分析图5(a)可知,D-HBSM可由全桥电路改进而来,而全桥电路的实际应用已经相对成熟,因此B型子模块的应用难度降低。为了简化电路,采用带箭头的线表示开关器件,其中红色箭头代表该器件开通,此时可以流过电流;黑色箭头代表该器件关断,此时不能流过电流,图6(b)也采用类似表示方法。对于B型子模块而言,在旁路模式下,子模块内2个电容被切除,B型子模块输出电压为0;在串联模式下,子模块内2个电容串联连接,B型子模块输出电压为Uc;在并联模式下,子模块内2个电容并联连接,B型子模块输出电压为0.5Uc。B型子模块中各电容值为2C,并联时B型子模块的等效电容为4C,而串联模式下的等效电容仍为C。
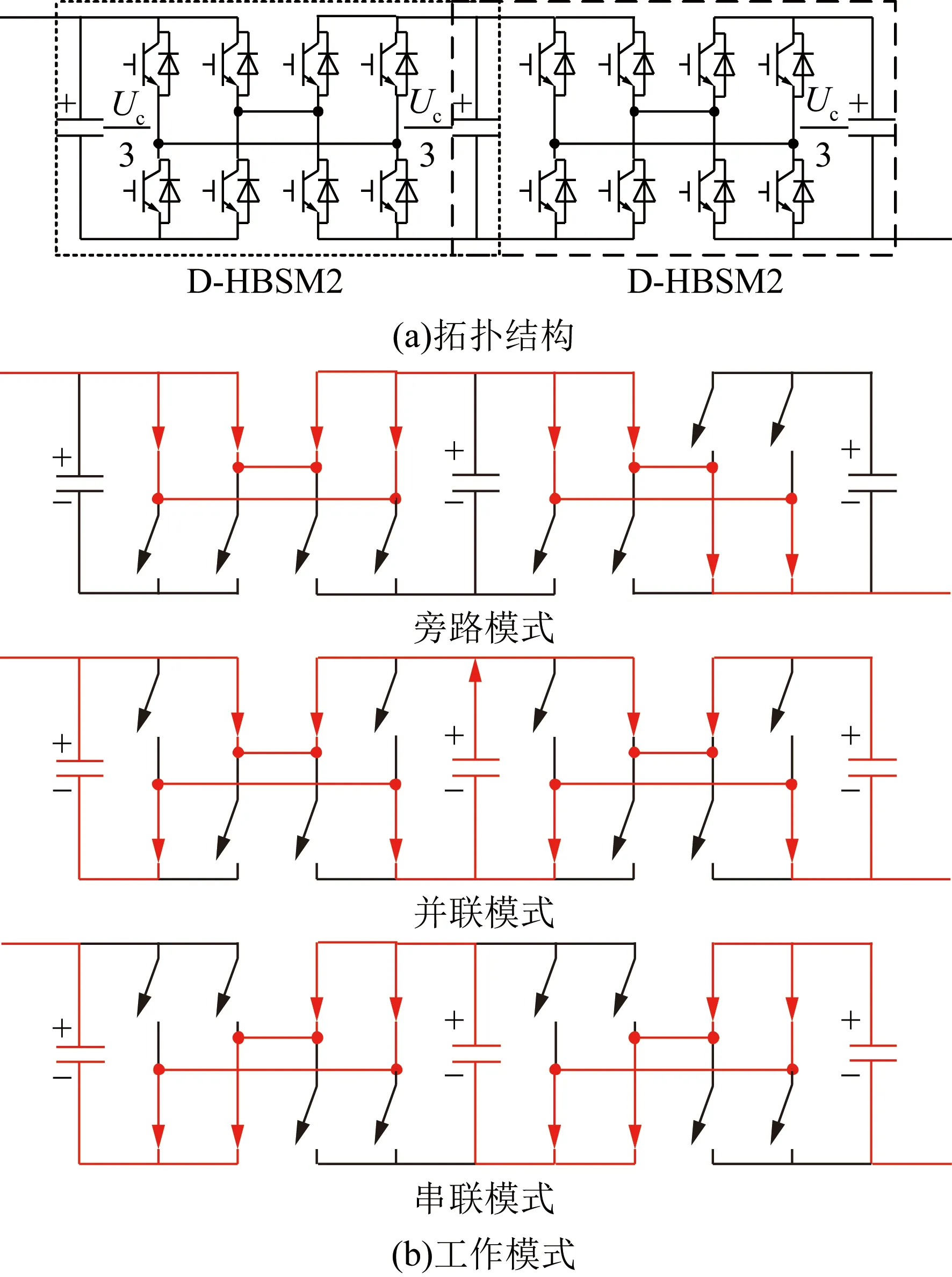
图6 B型子模块的拓扑结构及工作模式(d=3)Fig.6 Topology and working model of B-SM(d=3)
在LM-MMC中,A型子模块功率器件的耐受电压和通流能力分别为Uc和iarm。根据图5(b)可以看出,正常工作时B型子模块内部2条电流通路共同分担桥臂电流iarm,功率器件的耐受电压和通流能力分别为0.5Uc和0.5iarm,其性能指标要求仅为A型子模块功率器件的一半。通过查阅器件手册可知,耐受电压和通流能力分别为0.5Uc和0.5iarm的器件成本远低于耐受电压和通流能力分别为Uc和iarm的器件,因此B型子模块的器件成本不会大幅增加[23]。
当d取2时,相邻整数电平之间增加了0.5Uc电平,理论上仅需要1个B型子模块即可将输出电平数目近似扩大2倍。然而,只配置1个B型子模块则无法通过轮换均衡电容电压,因此d取2时,LM-MMC各桥臂至少需要配置2个B型子模块。
图6(a)为d取3时B型子模块的拓扑结构,可由2个D-HBSM构成,其工作模式如图6(b)所示。图6(b)包括并联、串联和旁路3种模式,在旁路模式下,子模块内3个电容被切除,B型子模块输出电压为0;在串联模式下,子模块内3个电容串联连接,B型子模块输出电压为Uc;在并联模式下子模块内3个电容并联连接,B型子模块输出电压为0.33Uc,如果相单元非整数电平为0.66Uc,则由2个B型子模块同时并联输出非整数电平。B型子模块中电容值为3C,并联时子模块的等效电容为6C,串联时等效电容仍为C。当d取3时,相邻整数电平之间增加了0.33Uc和0.66Uc电平,如果采用轮换均衡电容电压,桥臂单元至少需要配置3个B型子模块。
对比图5(a)和图6(a)可知,每个B型子模块包含d-1个D-HBSM,因此B型子模块的拓扑结构随着d的增加而复杂。此外,随着d的增加,桥臂中需要配置的B型子模块数也增加,因此d取2或3较为合适。
当不考虑子模块的电能损耗时,电容电压的变化量由桥臂电流决定,A和B型子模块输出电压为Uc时的电容电压变化量ΔUc_s为:
(2)
式中:C为电容值;ic(t)为电容电流;Ts为充放电周期。
B型子模块输出电压为Uc/d时的等效电容为d2C,等效电容电压变化量ΔUc_p为:
(3)
因此,B型子模块总的电容电压变化量为dΔUc_p,即ΔUc_s/d,小于输出电压为Uc的子模块,因此所有投入电路的子模块电容电压变化量不同。
由于电容之间存在容差,流过相同电流时B型子模块内电容电压不同,并联输出时便会产生冲击电流。针对该问题,可在D-HBSM内引入缓冲电感L1和L2构成RLC电路,如图7所示。在缓冲电感的限流下,冲击电流大幅衰减,由于缓冲电感远小于桥臂电感,因此不会影响换流器的正常运行。
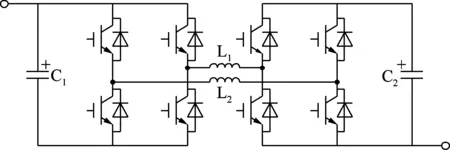
图7 冲击电流抑制策略Fig.7 Inrush current suppression strategy
3 电平多级倍增调制策略
3.1 调制原理
在传统MMC拓扑结构的基础上,通过引入B型子模块提供非整数电平,本文提出了一种电平多级倍增调制策略。以p=1、d=2为例,所提调制策略的原理如图8所示。此时阶梯电平的高度为Uc/2,Usm1为A型子模块的输出电压,Usm2和Usm3为B型子模块的输出电压。
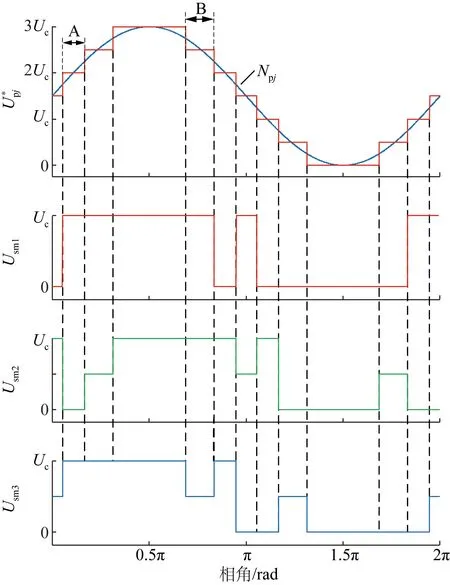
图8 电平多级倍增调制原理Fig.8 Principle of LMM
图8中,在A类排序区间输出整数电平,此时Upj=2Uc,经排序后Usm1输出值为Uc,Usm2旁路输出值为0,Usm3串联输出值为Uc;在B类排序区间输出非整数电平,此时Upj=2.5Uc,经排序后Usm1输出值为Uc,Usm2串联输出值为Uc,Usm3并联输出值为0.5Uc。
在电平多级倍增调制策略下,上下桥臂需要输出电平数Npj和Nnj分别为:
(4)
式中:round(·)为四舍五入取整函数。
以上桥臂为例,输出整数电平Npj_i为:
Npj_i=round(Npj)
(5)
非整数电平Npj_n为:
Npj_n=Npj-Npj_i
(6)
上桥臂投入子模块数Npj_in为:
Npj_in=Npj_i+dNpj_n
(7)
在LM-MMC中,输出电平数No与A、B型子模块的个数p、d的关系为:
No=d(p+2)+1
(8)
当桥臂单元输出电压为Uc(p+2-1/d)时,桥臂中p+1个子模块输出电压为Uc,d-1个子模块输出电压为Uc/d,桥臂中所有子模块均投入。当桥臂单元输出电压为Uc(p+2)时,桥臂中有p+2个子模块输出电压为Uc,此时桥臂中有d-2个子模块处于旁路状态,当d为2时,所有B型子模块都能够得到充分利用。
3.2 子模块工作模式流程
根据3.1节分析,B型子模块内各电容的工作状态相同,因此电容之间的电压偏差较小,B型子模块内各电容电压之和可以精确反映任意电容电压,可将B型子模块随A型子模块共同参与排序,通过子模块轮换实现电容电压均衡。以p=4、d=2为例,所设计方法原理如图9所示,A和B类排序区间分别代表输出整数和非整数电平。在A类排序区间,不需要输出非整数电平,经排序后确定子模块的工作模式;在B类排序区间,需要输出非整数电平,因此优先确定B型子模块的工作模式以提供非整数电平,然后再确定剩余子模块的工作模式。
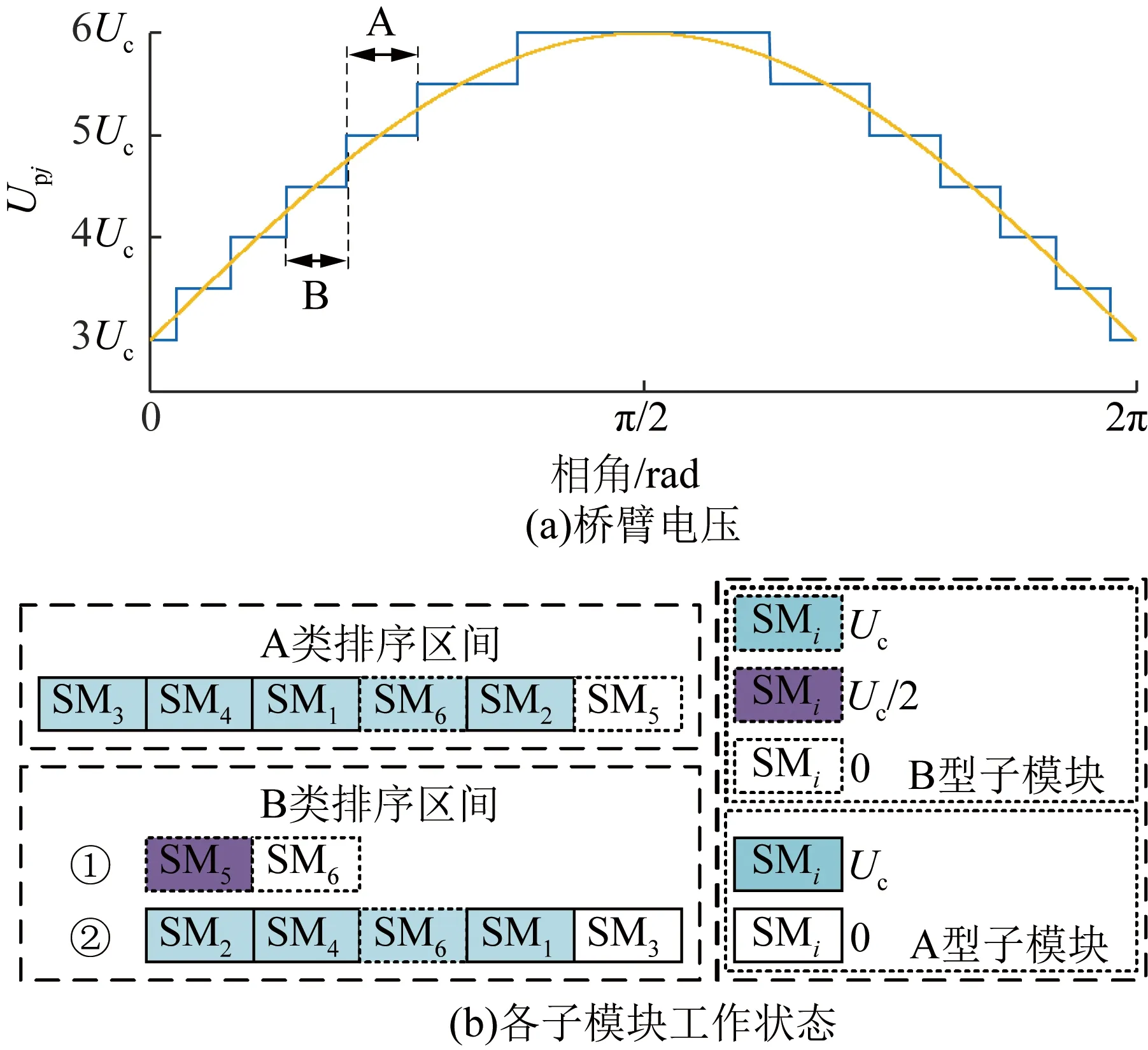
图9 电容电压排序原理Fig.9 Principle of capacitor voltage ranking
在所提电平倍增调制策略下,各子模块工作模式的确定流程如图10所示。当桥臂输出电平变化时轮换子模块,然后根据桥臂电流选择合适的子模块投入,均衡电容电压。首先分析上桥臂电流Ipj>0的情况,当输出整数电平时,优先投入A型和B型子模块中电压低的Npj_i个子模块,输出电容电压为Uc,其余子模块处于切除模式;当输出非整数电平时,首先投入Npj_n个电压低的B型子模块,并联输出电容电压为Uc/d,然后将剩余的B型子模块和A型子模块重新排序,投入电压低的Npj_i个子模块,其余子模块处于切除状态。类似地,可分析Ipj<0时子模块的工作模式,此处不再赘述。
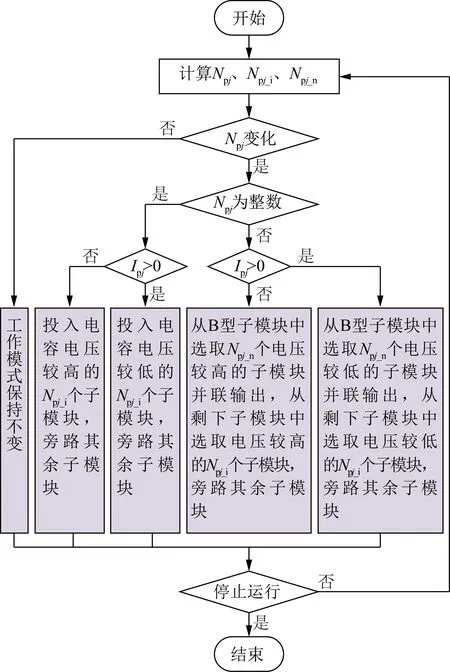
图10 工作模式确定流程Fig.10 Process of working mode determination
4 仿真验证与分析
本文在Matlab/Simulink平台中搭建仿真模型,验证所提LMM策略应用于LM-MMC拓扑的运行性能,并与NLM、CPS-PWM以及ELM[17]策略进行对比,仿真模型和参数分别如图11和表1所示。交流电压电平数目均为25,LM-MMC桥臂的A型和B型子模块数分别为10和2;传统MMC换流器的桥臂子模块数为12,并且采用文献[21]所提方法将NLM和CPS-PWM策略扩展至25电平,而ELM仍输出13电平,其中CPS-PWM的载波频率为500 Hz。采用文献[24]所示的分析方法计算4种调制策略的运行损耗。
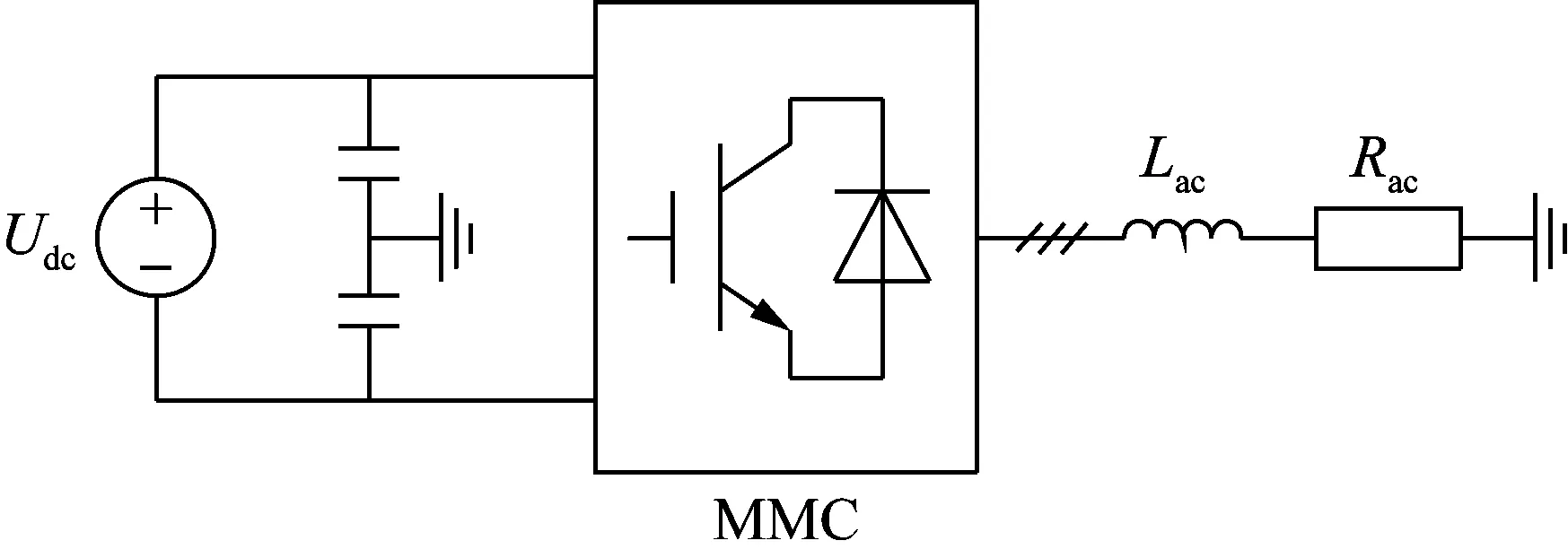
图11 仿真模型Fig.11 Simulation model

表1 仿真参数Table 1 Simulation parameters
4.1 调制策略对比
图12所示为适用于传统MMC的典型调制策略以及适用于LM-MMC的LMM调制策略的仿真结果。根据输出电压的波形和谐波畸变度可知,CPS-PWM在参考电压上叠加电压均衡信号,导致输出电压波形产生明显畸变。由于NLM和LMM的电压包括25个电平,而ELM只包含13个电平,因此ELM交流电压的低次谐波畸变度较高,而NLM的循环电流高于LMM,导致NLM的电压谐波含量也略微高于LMM。分析循环电流Icir的波形可知,NLM和CPS-PWM包含25个电平,其相单元输出电平数量变化,且CPS-PWM采用的复杂控制方法会大幅增加循环电流。而LMM和ELM的相单元投入子模块数量恒定,因此循环电流中的倍频含量明显低于NLM和CPS-PWM。对比子模块电容电压可知,NLM、ELM和LLM依靠排序算法实现电压均衡,电容电压波动趋势较为一致,而CPS-PWM依赖复杂的控制算法均衡电容电压,电容电压均衡程度较高,但是也会增加控制系统的负担。
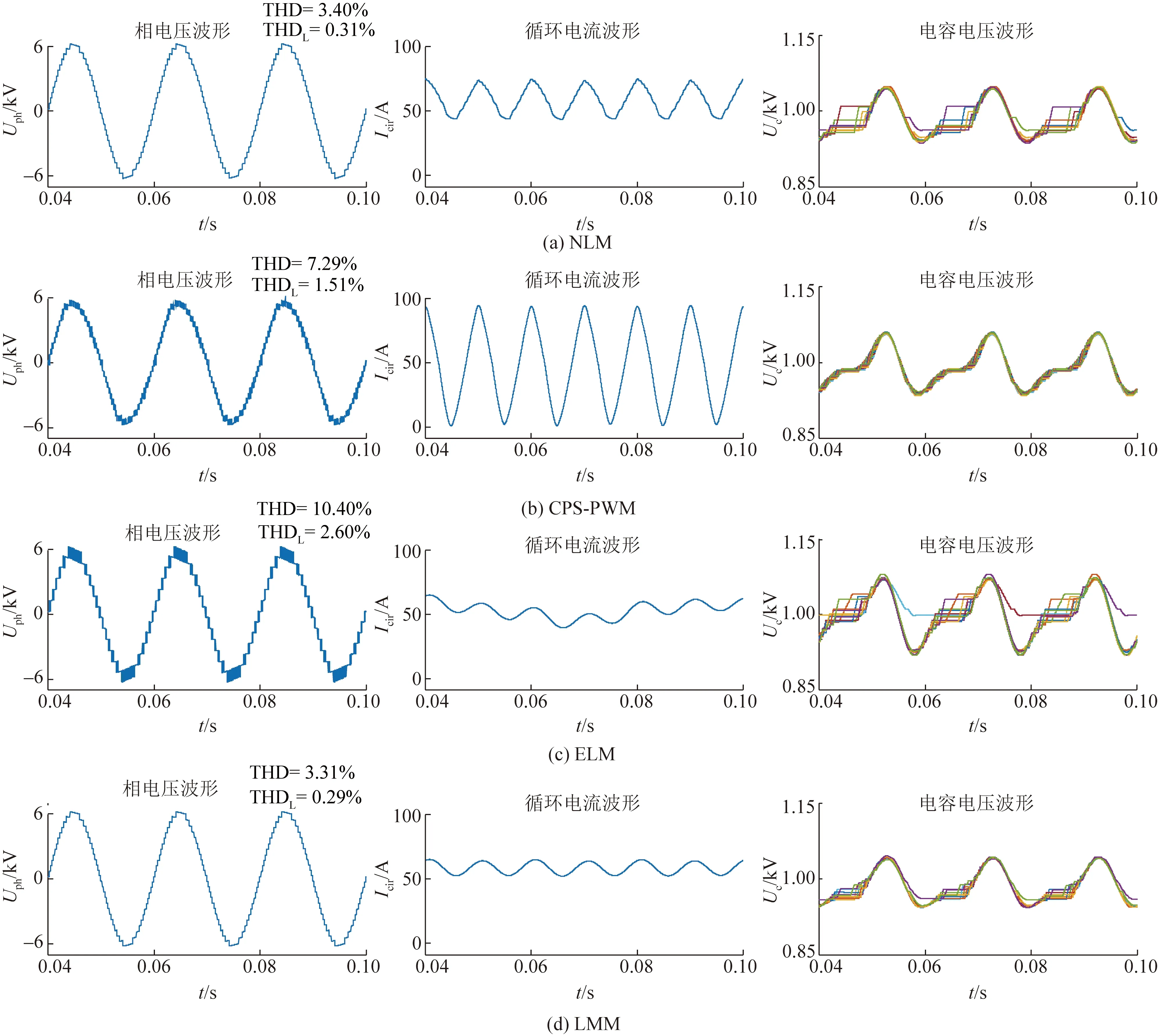
图12 四种调制策略的仿真结果对比Fig.12 Simulation results comparison of four modulation strategies
4.2 运行损耗对比
图13为4种调制策略的功率损耗对比结果。根据图13可知,当输出电平倍增时,CPS-PWM和NLM的循环电流大于LMM,这导致CPS-PWM和NLM的通态损耗均较高;由于CPS-PWM的开关频率较高,开关损耗也最高;而ELM中引入了方波脉冲,开关损耗也高于LMM,因此,LMM的运行损耗也最低,ELM则略微高于NLM,CPS-PWM最高。
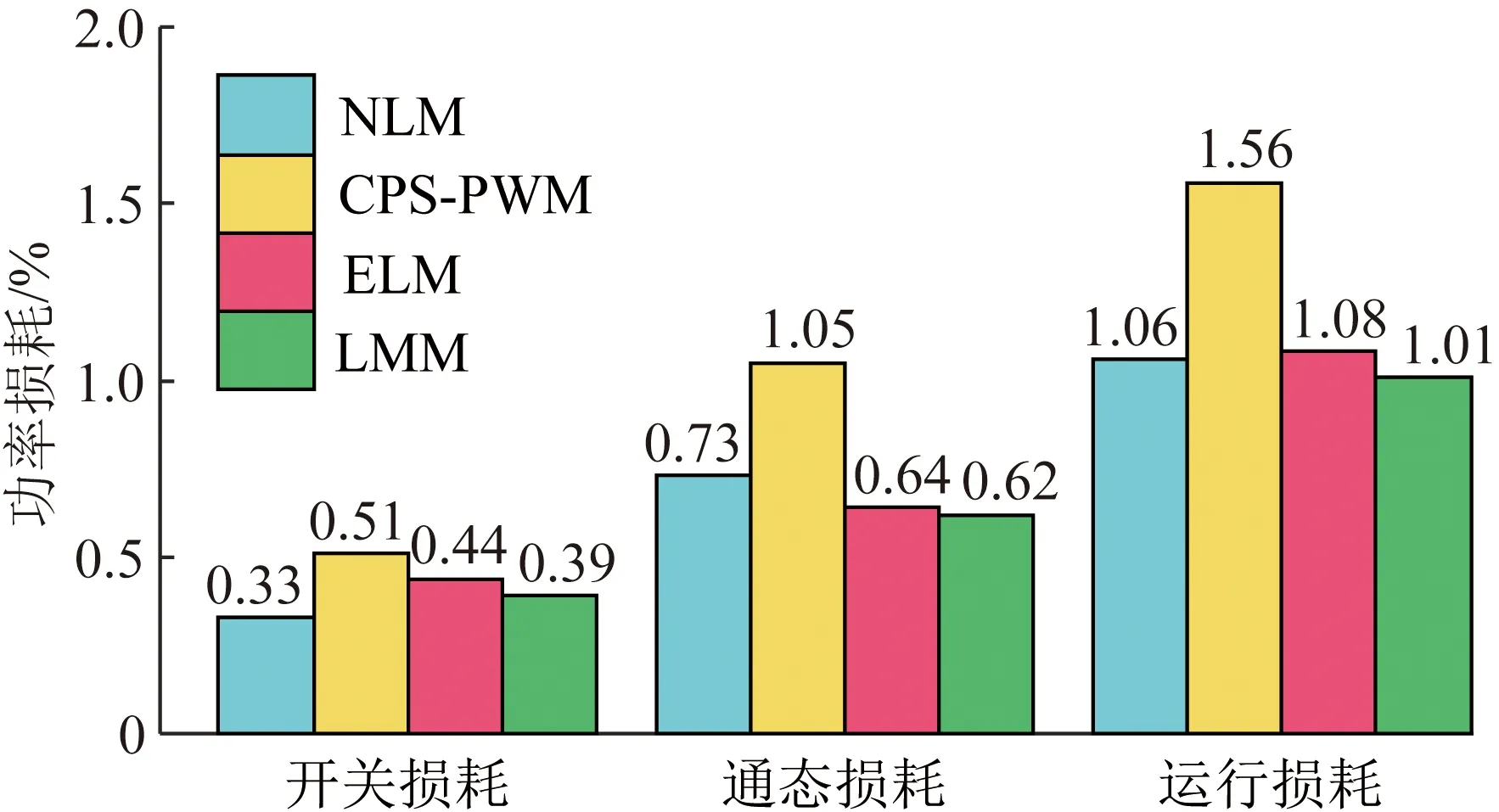
图13 四种调制策略的运行损耗Fig.13 Power loss of four modulation strategies
4.3 d=3的运行特性
如图12(d)所示,当p=10,d=2时LM-MMC的交流电压近似倍增,相邻整数电平之间只增加了一个1/2电平。图14为p=10,d=3时LM-MMC的交流电压、交流电流和电容电压的仿真结果。当d=3时,交流输出电压包含37个电平,相邻整数电平之间增加了1/3电平和2/3电平。对比图12(d)和图14可知,由于输出电平数目的增加,输出电压的谐波畸变度进一步降低,经过感性负载滤波后,电流波形质量得到进一步改善。
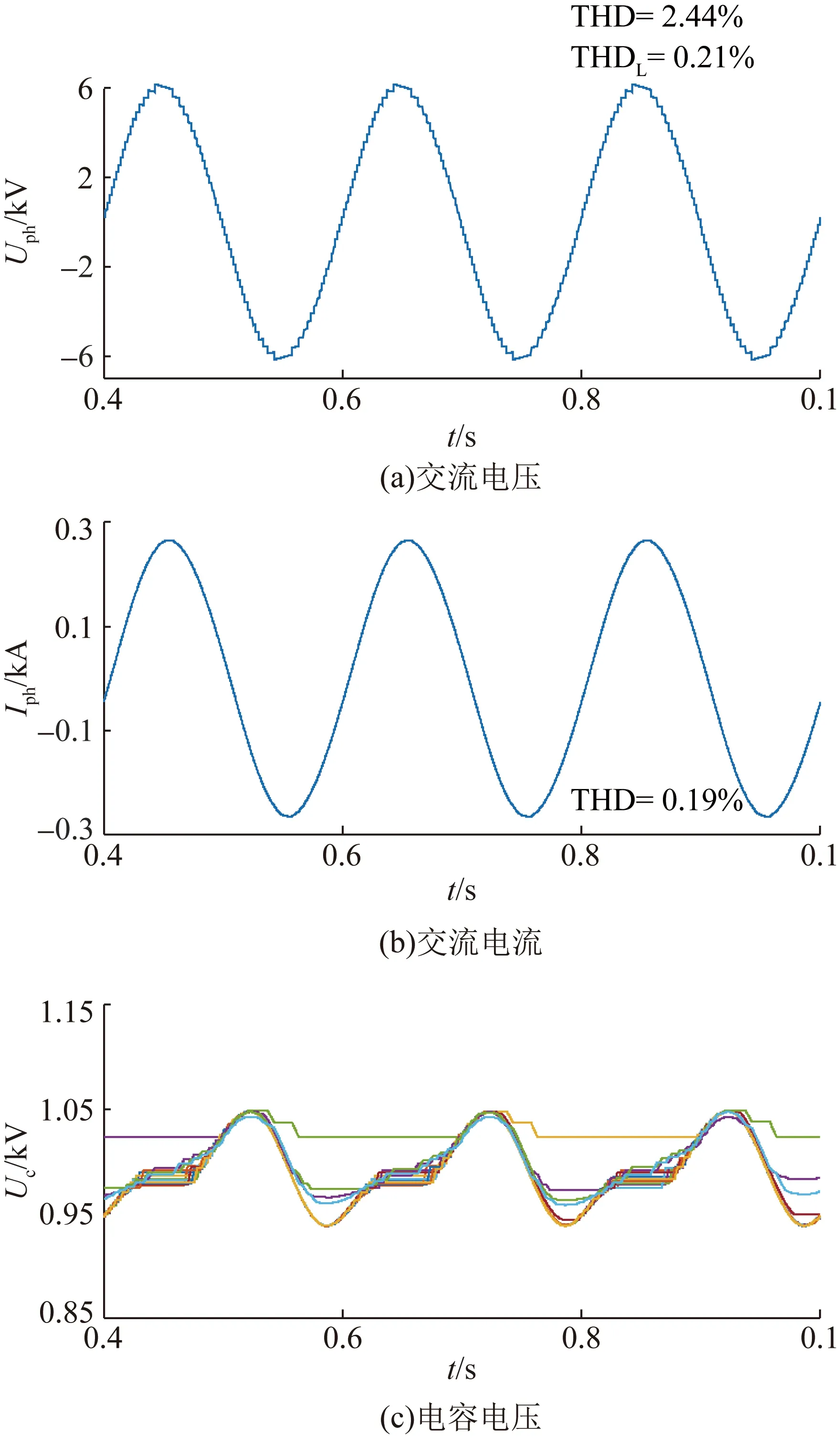
图14 d=3时的仿真结果Fig.14 Simulation results when d=3
LM-MMC通过引入d个具有非整数电平输出能力的B型子模块,输出电平近似扩展d倍,进而大幅提高输出电压和电流的波形质量。而且LMM策略通过轮换子模块的工作模式均衡电容电压,不需要采用复杂的电压均衡控制策略,功率器件的开关频率和换流站的运行损耗大幅减小,换流站正常运行时经济性较高。虽然B型子模块所采用功率器件数目较多,但是功率器件性能指标的要求较低,而且B型子模块数目较少,因此对于换流站成本影响较小。此外,B型子模块所采用的D-HBSM可由全桥电路改进而来,而全桥电路的实际应用已经较为成熟,因此B型子模块的应用难度得以降低。综上所述,当本文所提LMM策略应用于LM-MMC时,功率损耗较低,且输出波形质量较高。
5 实验验证
为进一步验证所提LM-MMC拓扑结构以及LMM策略的可行性,本文搭建了如图15所示的LM-MMC物理实验模型,具体参数如表2所示。直流电源的交流端口连接交流系统,直流端口连接LM-MMC直流侧,MMC交流侧连接星型感性负载,LM-MMC中d为2。
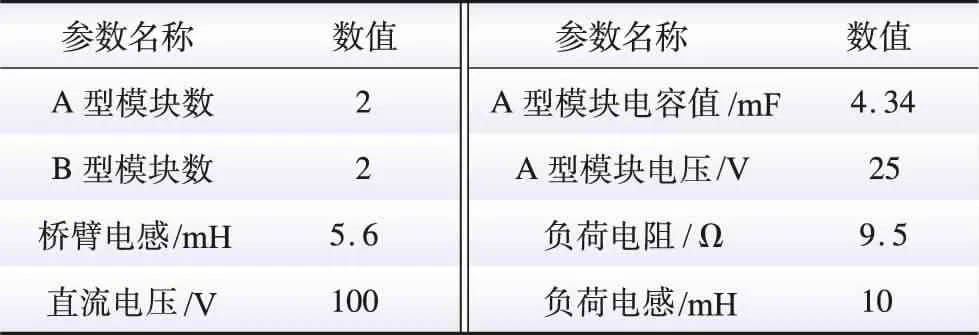
表2 实验参数Table 2 Experiment parameters
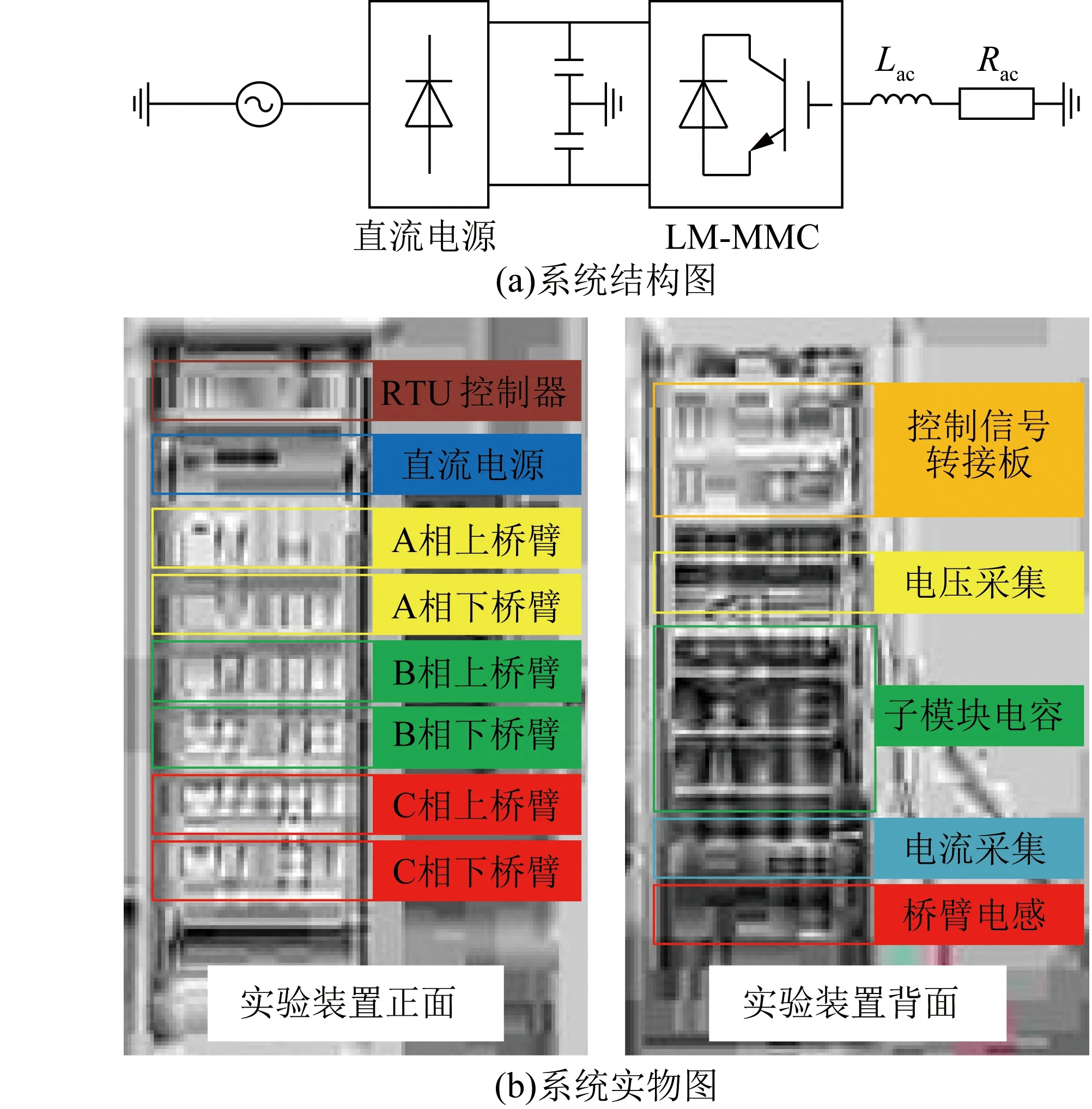
图15 实验系统Fig.15 Experiment system
图16为所提LM-MMC拓扑以及LMM策略的物理实验结果。图16(a)给出了桥臂单元4个子模块的输出电压波形(示波器电压范围为-10~40 V),Usm1和Usm2为A型子模块输出电压,其值为0或Uc;Usm3和Usm4为B型子模块输出电压,其值为0、Uc/2、Uc,任意时刻最多只有一个子模块输出电压为Uc/2。图16(b)所示为MMC交流侧输出电压和电流(示波器电压范围为-60~60 V,电流范围为-6~6 A),由于B型子模块的并联输出电压为Uc/2,可将交流电压扩展至9电平,减小了交流电压的低次谐波,经感性负载的滤波作用,交流电流波形质量较高。根据图16可知,实验结果和上文所述的理论分析以及图12所示的仿真结果相吻合,这证明LMM策略及其LM-MMC拓扑在实际工程中的可行性。
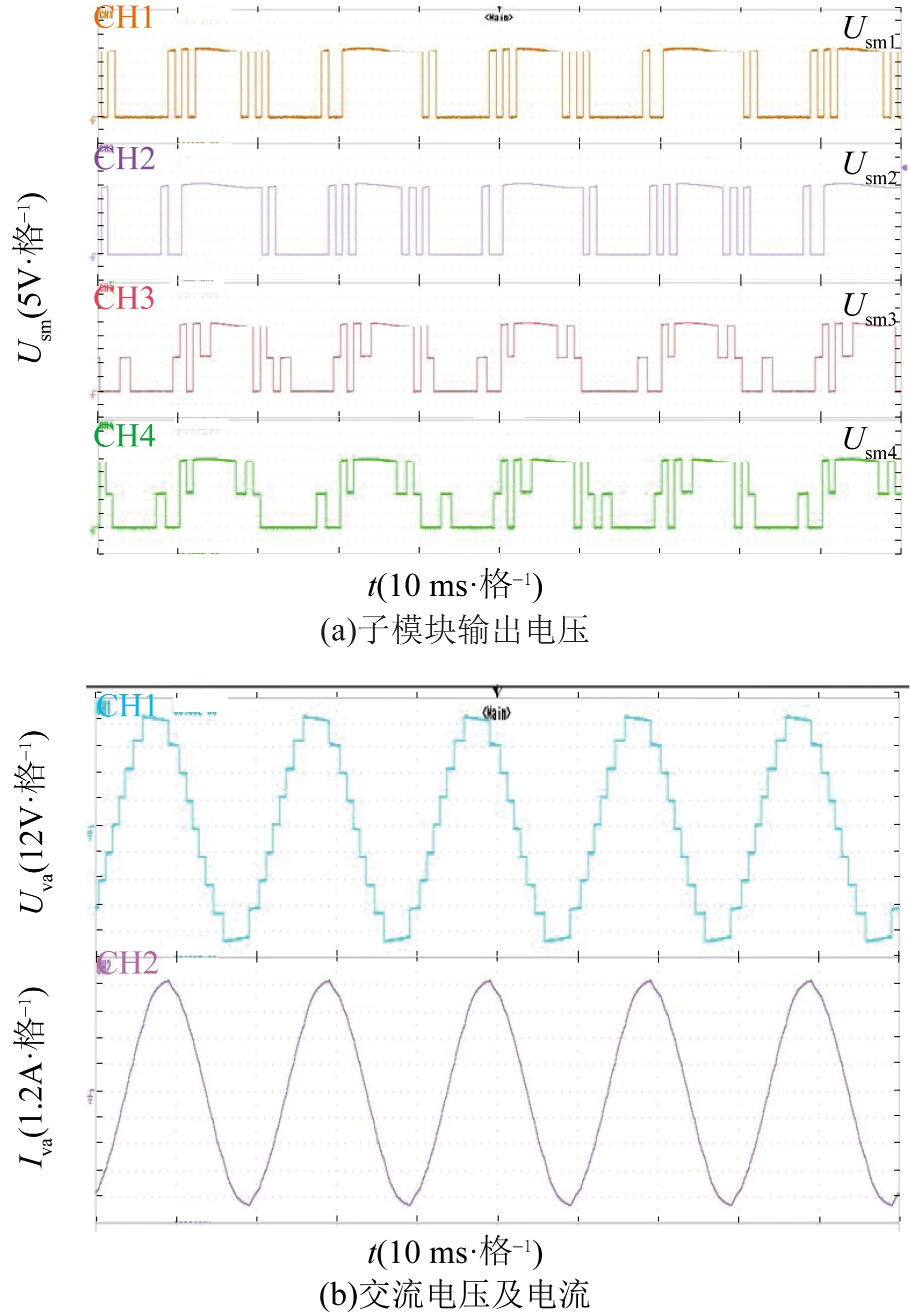
图16 实验结果Fig.16 Experiment results
6 结 论
本文设计了一种适用于中压直流系统的LM-MMC拓扑及其LMM策略,阐述了该拓扑及其调制策略的运行原理,设计了基于轮换的电容电压均衡策略,并且搭建Matlab/Simulink仿真模型和物理实验系统验证其可行性,得到以下结论:
1)采用具备并联输出非整数电平的B型子模块,所提LMM的交流电平多级倍增,减小了电压谐波畸变,改善了换流器的运行性能。
2)在所提LMM策略下,A型子模块输出整数电平,B型子模块主要输出非整数电平,根据电容电压排序结果确定子模块工作模式,可以有效均衡电容电压。
3)当所提LM-MMC拓扑应用LMM策略时,上下桥臂输出电平数量之和恒定,相单元电压均衡度较高,循环电流较低。此外,运行损耗低于相同条件下的NLM、ELM、CPS-PWM。
4)本文通过引入缓冲电感构成RLC电路,在电感的限流作用下,冲击电流被大幅衰减。然而目前实际工程中缺乏相关应用,其工程可行性有待进一步研究。
