考虑温度效应的风电增速箱动力学特性研究

赵荣珍, 花志锋

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

在风电产业中,受随机风载驱动的增速箱是决定整个风电机组安全可靠运行的关键部件.因其结构复杂故该部件在整个传动链中最易发生故障.因此对风电机组增速箱的动力学特性及其故障发生与演化机理进行更进一步的深入探讨,这对于提高整个风电机组的设计技术水平都具有积极的科学意义和工程应用参考价值.

近年来,为能够揭示风电增速箱的动力学特性及其故障发生机理,国内外对与之相关的动力学建模问题都在进行着深入的理论探讨.针对这种特定结构型式的齿轮传动系统,建立的动力学模型主要包括仅考虑齿轮扭转振动的纯扭转模型[1-4]和同时考虑齿轮径向振动与扭转振动耦合作用的平移-扭转模型[5].然而，随着在建模期间考虑的影响因素逐步增多,尽管如支撑刚度[6]、时变风载及齿轮裂纹故障[7-10]等干扰因素的影响被纳入增速箱动力学模型中,但根据集中质量法得到的建模结果在性能模拟计算中,但普遍存在着分析过程过于繁琐、难以实现模块化编程计算等缺点.目前，这方面的缺陷已经成为了严重阻碍风电增速箱动态设计理论向前发展的不利因素.对于如何改变当前这种困局,参考文献[11-14]提出的行星轮系耦合建模方法不仅简化风电增速箱动力学模型的建模过程,而且在降低其动态性能仿真计算模块化编程的难度方面,非常具有参考价值.

在提高风电增速箱的动力学建模精度方面,一个新的值得重视的问题便是齿面接触温度及其引起的齿廓热变形对啮合刚度的影响.针对该问题,目前已经建立了包括直齿轮[15]、斜齿轮[16]在内的2类考虑温度影响作用的刚度计算模型.并在此基础上分析摩擦与热变形[17]对齿轮动力学响应的影响.此外,在齿面胶合故障的研究过程中,齿面闪温参数被确定为目标参数,用来建立抗胶合齿轮修型优化模型[18].实际上，在考虑温度效应及其引起齿面胶合故障的问题中,以上文献已经取得了一些极具参考价值的研究进展.但对于在随机风载作用下的风电增速箱,关于齿面温度效应对其动力学性能影响的研究却鲜少报道.

鉴于此,本研究对在随机风载作用下齿轮齿面接触温度的变化规律进行分析，同时探讨齿轮齿面接触温度对风电增速齿轮箱动态特性的影响，这将为进一步解决好风电增速齿轮箱的温升异常现象提供理论参考依据.

1 基本问题简介

本研究以广泛使用的1.5 MW水平轴式风电机组作为研究对象,针对温度效应对其动力学特性的影响进行分析.该类风电机组增速箱传动系统的结构如图1所示,它由一级行星轮系与两级平行轴斜齿轮传动串联组成.其中,输入扭矩由行星架H带动行星轮Z2-4,经与太阳轮Z5和内齿圈Z6啮合，再由两级平行轴齿轮Z7、Z8、Z9传动增速,最终由高速级斜齿轮Z10输出，Tin与Tout分别为风电增速箱的输入与输出转矩.

图1 风电增速齿轮箱传动系统结构图Fig.1 Structure diagram of the transmission system of wind power increasing gearbox

针对图1所示的模型,本研究通过建立考虑时变温度刚度作用下的风电齿轮传动系统动力学方程,分析了随机风载作用下齿面接触温度对复合轮系动态特性的影响规律.为此建立的广义方程为

(1)

根据式(1),在第2节中将为图1所示的风电齿轮传动系统建立动力学方程.

2 考虑齿面接触温度作用的增速箱动力学模型

2.1 多体系统的拓扑结构

在多体系统的研究过程中,由于拓扑结构可以高度地凝炼和概括整个系统的本质,所以使用拓扑结构对多体系统进行描述成为多体动力学理论的基础问题.参照图1所示的风电增速齿轮箱传动系统,根据多体系统动力学理论,采用刚体B0代表机架,刚体B1代表行星架,其余每个齿轮都看作独立的刚体并依次编号,分别用Bi(i=2,…,10)表示,得到如图2所示的拓扑结构.其中，用实线箭头表示系统中各个齿轮与机架之间的旋转铰,即Hi(i=1,2,3,4,11,12,14,16,18,20)；虚线箭头表示各个齿轮之间的啮合力,即Hi(i=5,…,10,13,15,17,19).为了进一步研究该系统的连接关系,根据多体动力学原理,将图2所示拓扑结构中的齿轮副时变啮合力按照力元进行处理,即将图中虚线箭头全部切断,则得到该传动系统的树系统拓扑结构如图3所示.

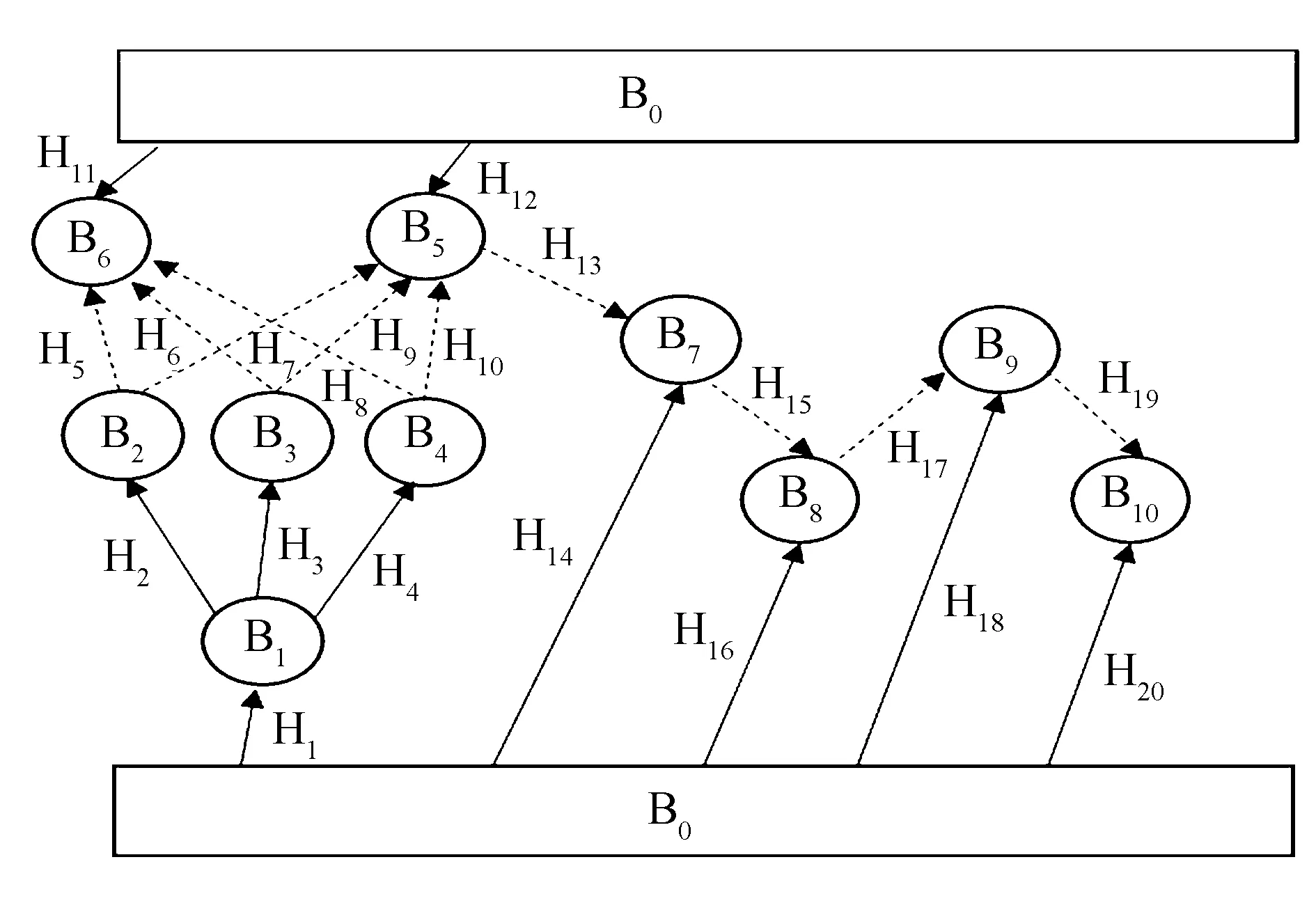
图2 风电齿轮箱拓扑结构Fig.2 Topological structure of wind power gearbox

图3 等效树系统拓扑结构Fig.3 Topological structure of equivalent tree system

根据图3所示的树系统,建立系统质量矩阵M.由图3可知，B2～B10是末端刚体, 其标号在内接物体数组中不会出现,则内接数组L=[0,1,1, 1].系统中3条最长的路分别是L1=[2,1],L2=[3,1],L3=[4, 1].根据多体动力学原理,可知M为

(2)

其中,

ML1(1)L1(1)=ML2(1)L2(1)=ML3(1)L3(1)

ML1(2)L1(2)=ML2(3)L2(3)=ML3(4)L3(4)

ML2(1)L2(1)=ML1(1)L1(2)=ML2(1)L2(3)=

ML3(1)L3(4)=ML1(2)L1(1)=

ML2(3)L2(1)=ML3(4)L3(1)

式中：mc为行星架的质量;mp为行星轮的质量;ms为太阳轮的质量;mr为内齿圈的质量；斜齿轮Z7～Z10的质量采用mi(i=7,…,10)表示；各齿轮的转动惯量采用Ii(i=c,s,p,r,7,…,10)表示；行星轮的基圆半径采用rbp表示.

2.2 齿轮副的啮合模型

在齿轮啮合模型中,沿齿轮副啮合线上的相对位移直接决定了齿轮副之间啮合力的大小.故采用式(3)表示考虑啮合误差的第i对行星轮-太阳轮和行星轮-内齿圈沿啮合线上的相对位移及平行轮系齿轮副Z7～Z8和齿轮副Z9～Z10沿啮合线上的相对位移，即

(i=sp,rp;j=7-8,9-10)

(3)

式中:Wsp、Wrp、W7-8、W9-10分别为行星轮-太阳轮、行星轮-内齿圈、齿轮Z7-Z8及齿轮Z9-Z10在广义坐标沿啮合线方向上的投影矢量；Xsp、Xrp、X7-8、X9-10分别为行星轮-太阳轮、行星轮-内齿圈、齿轮Z7-Z8及齿轮Z9-Z10啮合副的位移矢量；esp(t)、erp(t)、e7-8(t)、e9-10(t)分别为为行星轮-太阳轮、行星轮-内齿圈、齿轮Z7-Z8及齿轮Z9-Z10啮合副的综合啮合误差[2].

其中，

(4)

(5)

式中：ψsp=φi-αsp，ψrp=φi-αrp，φ=wct+φi分别为行星轮i的位置角；wc为行星轮角速度；φi=2π(i-1)/3为行星轮的初相位；αsp为行星轮-太阳轮的压力角;αrp为行星轮-内齿圈的压力角;α7-8、α9-10分别为齿轮Z7-Z8和齿轮Z9-Z10的压力角;rbs、rbp、rbr分别为太阳轮、内齿圈、行星轮的基圆半径;rb7、rb8、rb9、rb10分别为齿轮Z7～Z10的基圆半径;各构件在x、y、θ方向的振动位移用xk、yk、θk(k=s,pi,r,7,…,10)表示.

根据图4所示的力学分析模型和式(3)中沿啮合线的相对位移可知,齿轮副的时变啮合力为

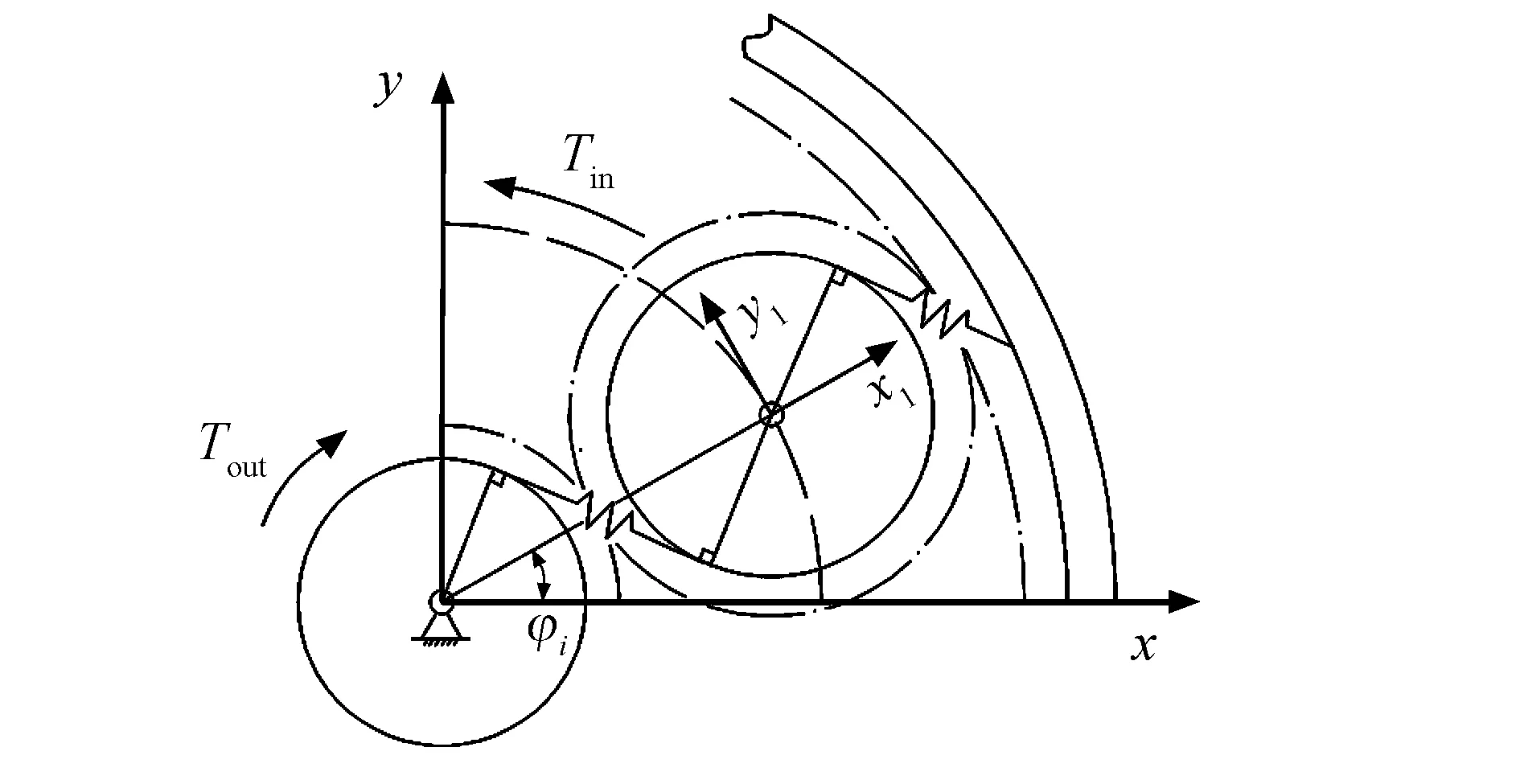
图4 行星轮系的力学分析模型Fig.4 Mechanical analysis model of planetary gear train

(6)

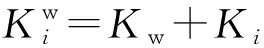
同时，将式(6)中的时变啮合力进行组装可得系统的时变啮合力矩阵：

(7)

2.3 轴承支撑刚度与阻尼模型计算矩阵

在图1所示的风电增速箱传动系统中,考虑到各齿轮轴与机架采用轴承连接,故将轴承的支撑力等效为阻尼力与弹簧力的合力.因此，行星轮-行星架轴承支撑刚度矩阵为

(8)

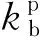
根据材料力学假设各轴承-轴组件均具有各向同性特性,则该传动系统中其余各轴承的支撑刚度矩阵为

(9)

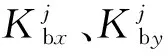
由于行星轮与行星架之间存在相对运动,所以在行星轮系建模过程中,行星轮的陀螺矩阵与离心矩阵被考虑，即

(10)

式中：wc为行星架的转动角速度；mp为行星轮的质量.

2.4 齿轮与齿轮轴的扭转模型

设太阳轮与齿轮Z7及齿轮Z8-Z9沿连接轴方向上的相对位移为

(11)

式中：Ws-7、W8-9分别是太阳轮-齿轮Z7与齿轮Z8-Z9在广义坐标下沿连接轴方向的投影矢量；Xs-7、X8-9,分别是太阳轮-齿轮Z7与齿轮Z8-Z9在广义坐标的位移矢量.即

(12)

其中，rbs为太阳轮的基圆半径.

则齿轮轴传递的扭矩在广义坐标下的投影为

(13)

式中:Ki(i=s-7,8-9)为齿轮轴的扭转刚度;Ci(i=s-7,8-9)为齿轮轴的等效扭转阻尼[5].

齿轮轴传递扭矩的广义力矩阵为

Ft=[0,0,…,0,Fs,0,F7,F8,F9,0]T

(14)

2.5 风电增速齿轮箱传动系统的动力学方程

根据式(1)，建立的风电增速齿轮箱动力学方程的矩阵形式为

(15)

式中：刚度矩阵Kcp为行星架与行星轮之间的轴承刚度；Kb为各构件与齿轮箱体之间的轴承刚度.即

式(15)中的广义外力矩阵为

Fc=[0,-mcg,Tin]

Fpi=[-mpgsinφi,-mpgcosφi,0]

(i=1,2,3)

Fj=[0,-mjg,0](j=s,r,7,8,9)

F10=[0,-m10g,-Tout]

F=[Fc,Fp1,Fp2,Fp3,Fs,Fr,F7,F8,F9,F10]T

(16)

3 齿轮齿面接触的温度刚度模型

基于Block闪温与Hertz接触理论并引用文献[15]所建立的温度刚度模型,本节将推导随机风载对温度刚度影响的计算模型.

3.1 齿面接触温度计算模型

齿面接触温度Tc主要包含齿轮本体温度Tb与齿面瞬时闪温Ts，即

Tc=Tb+Ts

(17)

在齿轮副啮合过程中,相互接触的2个轮齿齿面产生相对滑动,将齿轮副所传递的部分机械能通过齿面摩擦的形式转化成热能,进而引起齿轮副啮合区域的温度升高,该温度被称为齿面瞬时闪温[15], 即

(18)

式中:u为摩擦系数;Fe为单元齿面上的法向载荷；gi为齿面热传导系数,i=1,2；ci为比热容；ρi为齿面材料密度；vi为主、从动齿轮在啮合点处随时间t变化的切向速度,表达式为

vi(t)=wirci(t)sin(arccosαpi)

(19)

式中:wi为主、从动齿轮的角速度；αpi为齿轮啮合点处压力角；rci(t)为主、从动齿轮旋转中心到啮合点处的距离,表达式[15]为

(20)

式中:rbi为齿轮基圆半径;ra2为从动齿轮齿顶圆半径;w1为主动轮角速度;α为齿轮压力角.

假设主、从动齿轮的材料相同,根据Hertz接触理论可知,主、从动齿轮的接触半带宽Bh为

(21)

式中:η=1.128;μ为泊松比;Ri(t)为啮合点处主、从动齿轮的曲率半径[15],即

Ri(t)=rci(t)sinαpi(t)

(22)

3.2 齿面接触温度引起的齿廓变形计算模型

在3.1节中讨论了由于齿面摩擦使部分机械能转化成齿面瞬时闪温,导致齿面接触温度发生变化,进而造成齿轮的实际齿廓曲线与理论齿廓曲线不重合,并引起齿廓热变形.若忽略其他因素的影响,那么仅考虑齿面接触温度变化引起的主、从动齿轮齿廓变形为

(24)

式中：齿面闪温TΔ为系统进入稳态后,齿面接触温度Tc与初始齿面温度T0之差;b为齿轮的分度圆齿厚;λ为线膨胀系数;αpi=arccos(rbi/rai)为齿轮齿顶压力角;ubi为稳态时齿轮的基圆形变量[15]，即

(25)

式中：Troi为稳态时主、从动齿轮轴的温度；Trbi为稳态时主、从动齿轮基圆上的温度；roi为主、从动齿轮的分度圆半径.

3.3 齿面接触温度变化引起的时变温度刚度

根据Hertz接触理论,假设作用于齿面的法向载荷为FN,齿面接触温度引起的齿廓变形为εi,则单个齿轮的时变温度刚度为

Kwi(t)=FN/(bεi)

(26)

分别代入主、从动齿轮的齿廓变形ε1、ε2.假设啮合时两齿面接触温度引起的齿面变形在同一条直线上,则等效时变温度刚度[15]为

Kw(t)=Kw1(t)Kw2(t)/[Kw1(t)+Kw2(t)]

(27)

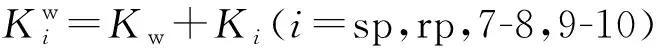
4 双参数威布尔随机风速模型

本节引用文献[4]所述的双参数Weibull模型对风速进行模拟,并根据风轮捕获功率模型推导输入风电增速齿轮箱的时变转速和时变扭矩.大量研究表明,双参数Weibull分布曲线可以有效表示某地区的风速特性,其概率密度函数为

(28)

式中:k为形状参数；c为尺寸参数；v为随机风速.

由统计学原理可推导出风速的数学期望和方差，即

(29)

通过求解E(v)和D(v)可以求得形状参数k和尺寸参数c,得到的近似表达式为

(30)

采用风能捕获功率的数学计算模型可得出输入增速齿轮箱的时变扭矩和时变转速的表达式[4]分别为

式中：Te为额定转矩；Ve为额定风速；ne为额定转速；Vcutoff、Vcutin为风轮的切入风速、切出风速.

5 算例分析

针对图1所示的1.5 MW水平轴式风电机组增速箱结构模型,在随机风载作用时对其进行动力学性能仿真.用于模拟计算的风电机组参数包括额定功率1.5 MW、风轮直径65 m、风轮额定转速19.8 r/m.关于增速箱的基础参数如表1所列.

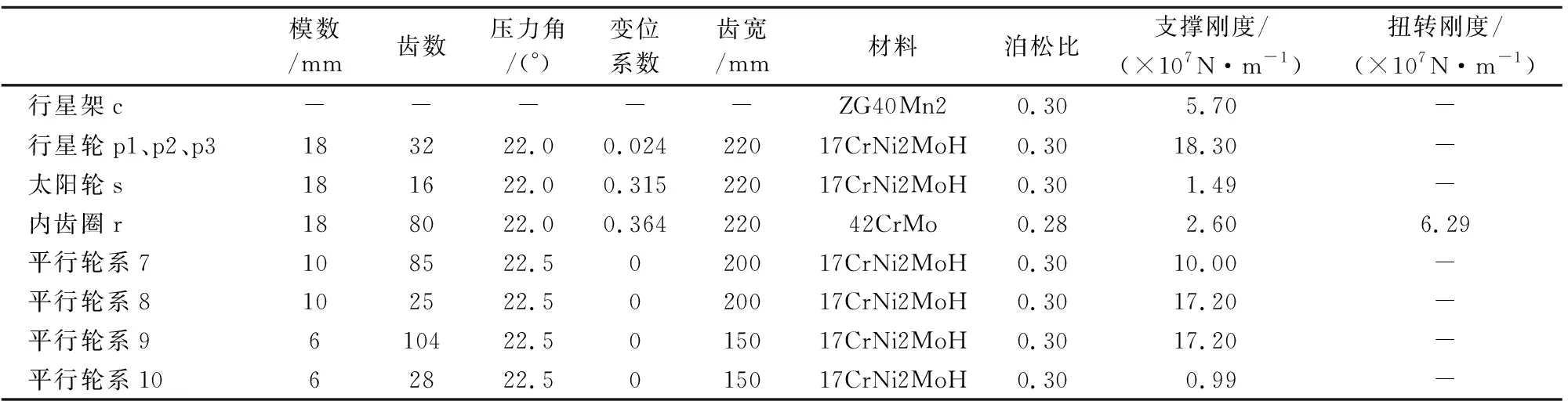
表1 齿轮传动系统基础参数

5.1 随机风速载荷对齿面接触温度的影响

为了进一步研究输入转矩对齿面闪温的影响,将15 s内的输入转矩作为时变温度刚度的输入参数,仿真计算齿轮啮合过程中齿面闪温和时变温度刚度.齿轮传动系统各齿轮的相关参数如表2所列.

由Weibull分布函数建立的随机风速模型模拟得到的15 s内输入转矩曲线如图5所示.可以看出，在初始时刻至15 s时,由于风速发生改变,所以输入增速齿轮箱的扭矩也发生改变,同时两者变化规律相同.

图5 仿真15 s内系统输入转矩曲线Fig.5 System input torque curve within 15s of simulation

使用表2中的参数,对时变温度刚度模型进行仿真计算,结果如图6和图7所示.图6为齿轮传动系统受随机风载影响在摩擦系数fm=0.06时,太阳轮-行星轮齿面闪温TΔ随时间变化的趋势.可以看出：当t=0.74 s时,TΔ=55.27 ℃，达到整个区间最大值；当t=11.0 s时,TΔ=2.55 ℃，达到整个区间最小值.齿面闪温数值在整个时间区域内部反复波动，这是由于齿轮在啮合过程中,当主动齿轮从齿根处啮合时,齿轮的齿面闪温达到极大值,随着齿轮的转动,在接近齿轮的节点时齿面相对滑动速度最小,齿面闪温达到极小值,之后随着啮合过程的继续齿面闪温逐渐升高,当到达下一个轮齿的齿顶时,闪温出现极大值.该结果与文献[16]结论一致.将闪温曲线与输入扭矩曲线对比,不难看出齿面闪温曲线的低频部分主要受到输入转矩的影响.

表2 齿轮参数

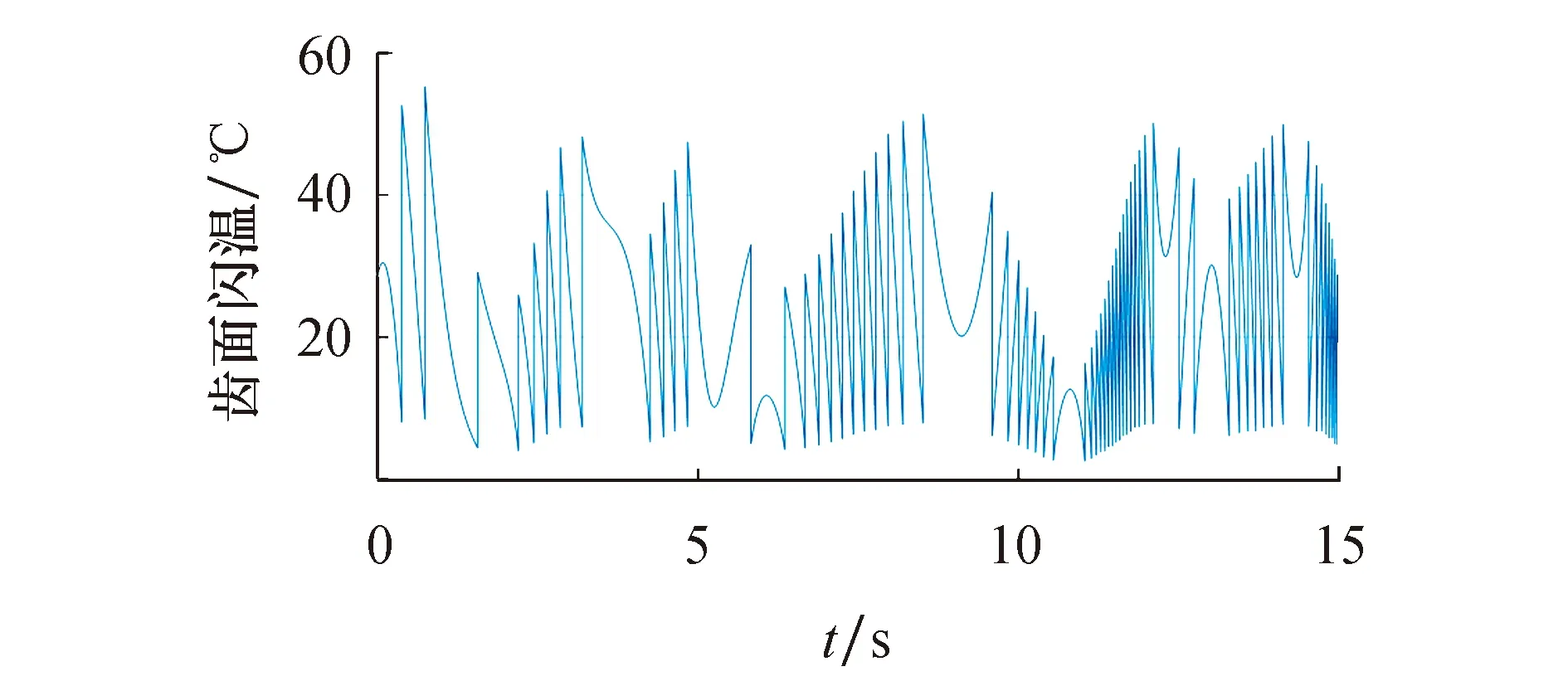
图6 齿面闪温变化趋势图Fig.6 Trend of flash temperature change of tooth surface

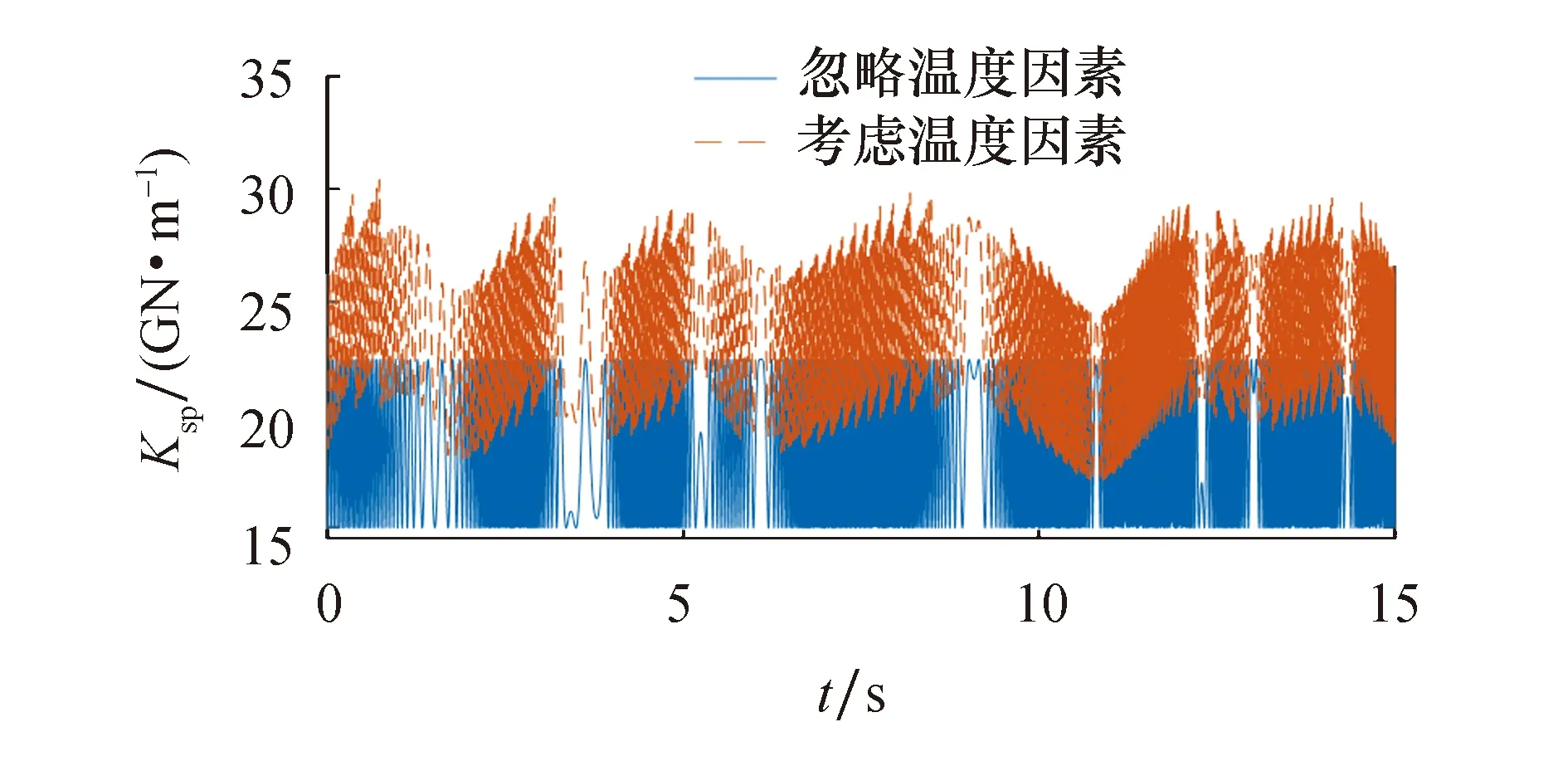
图7 温度因素对时变啮合刚度的影响

图7为考虑温度因素和忽略温度因素的太阳轮-行星轮时变啮合刚度随时间变化的趋势.由考虑齿面接触温度因素影响的时变啮合刚度可知,因两齿面接触温度的变化导致齿廓产生热变形,而齿轮齿廓的热变形会直接引起齿轮产生时变温度刚度.

根据文献[16],在计算齿轮刚度时,需要将齿轮的时变啮合刚度与时变温度刚度进行叠加,结果如图7所示.可以看出，在考虑温度因素的时变啮合刚度时,低频部分主要受到温度因素的影响，而高频部分主要受到齿轮啮合频率的影响.因此，齿轮齿面接触温度改变了太阳轮-行星轮的时变啮合刚度变化幅值.

5.2 考虑温度刚度对传动系统动态特性的影响

通过对比齿轮传动系统的时域响应和频域频谱,进一步研究温度效应对风电增速齿轮箱传动系统的影响.在Matlab软件中采用Runger-Kutta法，对第2节推导的风电增速箱齿轮传动系统动力学模型进行求解.通过对比时域和频域特征,分析温度因素对风电增速齿轮箱动态响应的影响.

图8为考虑温度作用下太阳轮的振动位移响应.由于行星轮系具有均载特性,故太阳轮的径向振动受随机载荷的影响较小,且其变化规律与风载的变化规律不一致.而太阳轮的扭转振动位移低频部分与输入转矩的变化规律基本一致,其高频部分的振动响应则主要受到行星轮-太阳轮的啮合频率影响.这表明,当输入转矩增大时,太阳轮扭转振动响应幅值会随之增大.

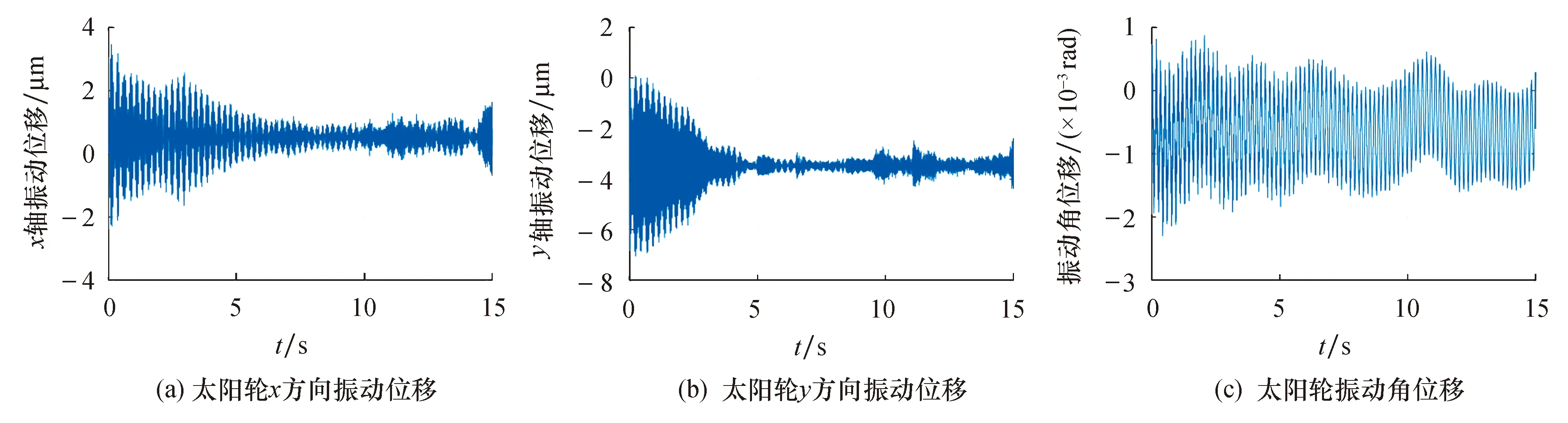
图8 太阳轮的振动位移响应Fig.8 Vibration displacement response of sun gear

图9为考虑温度作用下行星轮的振动位移响应.可以看出，当该系统输入转矩发生变化时,行星轮在3个广义坐标上的位移响应均受到了不同程度的影响.将行星轮平移方向和扭转方向上的振动位移与输入转矩进行对比可知,振动位移响应的低频部分主要受到输入扭矩的影响,而对高频部分影响较大的是太阳轮-行星轮的啮合频率.

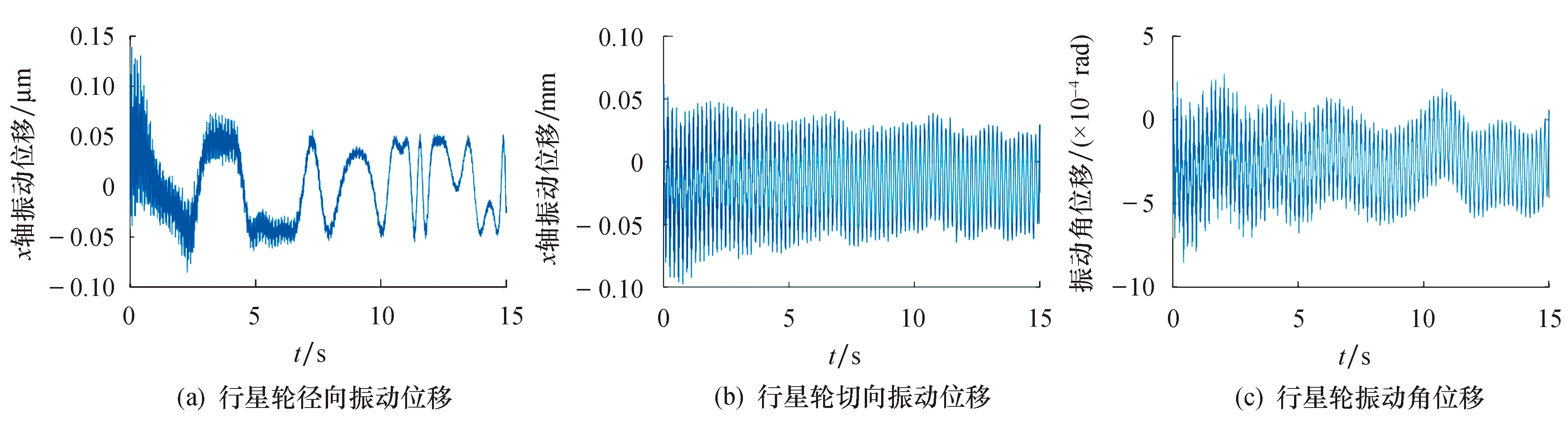
图9 行星轮的振动位移响应

为了研究温度效应对混合轮系动态特性的影响,使用图10所示的行星架相平面图进行对比分析.由于图10b所示的行星架相平面图考虑了温度效应对齿轮时变啮合刚度的影响,所以其振动位移与振动速度均相对较小.不仅如此，相比图10a，图10b所示曲线的外围更加散乱无序.因此，考虑温度因素会导致系统的振动位移和振动速度降低,同时系统动态响应更加复杂.

图10 行星架的相平面图

图11为行星架的振动角位移频谱图.可以看出：温度效应确实会降低行星架的振动位移幅值；因考虑温度效应的影响而导致行星架的频谱中不仅出现了行星轮系的啮合频率,同时还出现了温度变化产生的新激振频率.该结论与振动位移的分析结论一致.这说明，在仿真分析风电增速齿轮箱动力学响应时,齿面接触温度对该系统的影响不应忽略.

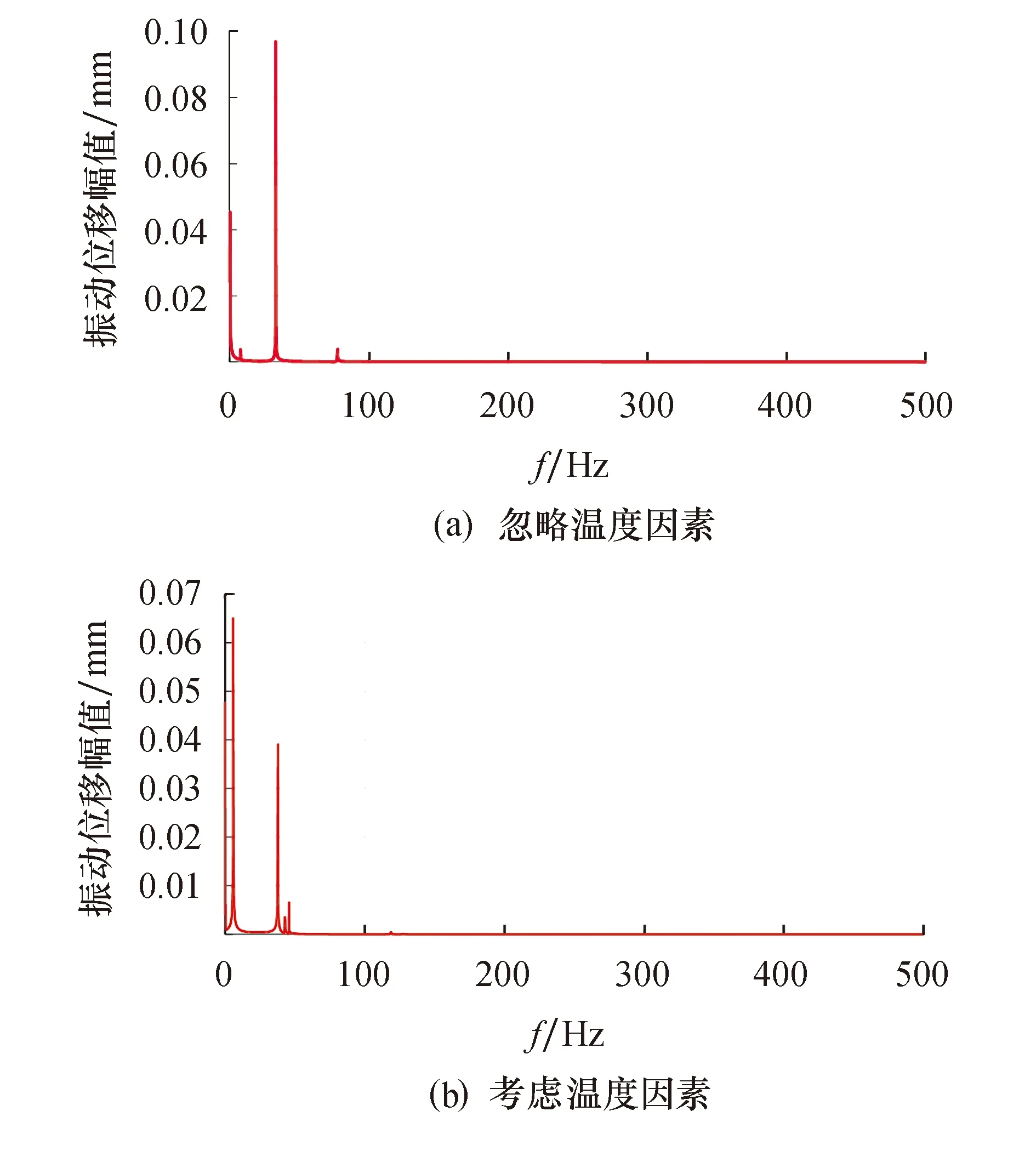
图11 行星架振动位移频域分析Fig.11 Frequency domain analysis of planetary carrier vibration displacement

6 结论

以风电增速箱为研究对象,分析了齿面接触温度对风电增速箱动态响应的影响.首先将行星齿轮耦合分析方法引入增速箱混合轮系的建模过程中,采用将混合轮系划分为行星轮系、平行轮系等结构单元的方式,建立了一种多级混合轮系的动力学模型.然后,通过该模型分析了随机风载对齿面接触温度及齿面接触温度对时变啮合刚度的影响；研究表明,在输入载荷发生随机动态变化时,齿面的接触温度会发生波动；通过分析温度效应对时变啮合刚度的影响，发现温度效应会影响时变啮合刚度的低频区域,而啮合频率会影响时变啮合刚度的高频区域.最后，将考虑温度效应的时变啮合刚度输入所建立的动力学模型中,通过分析齿轮啮合刚度和行星轮系的时频域信号,发现考虑齿面接触温度会导致齿轮传动系统的时域信号幅值降低,频域中出现因齿面接触温度产生的激励频率.研究表明，风电增速箱动力学分析过程中必须考虑温度效应的影响.