基于转子-轴承-干气密封系统静环振动分析
2022-05-08张伟政赵志宏洪海民
张伟政, 赵志宏, 姜 娥, 洪海民
(兰州理工大学 石油化工学院, 甘肃 兰州 730050)
干气密封作为旋转机械最常用的轴封形式,近年来在超临界二氧化碳机组及火箭发动机等领域得到广泛使用,在高速、高温、高压等特殊工况下干气密封的稳定性问题一直是国内外学者研究的难点.干气密封系统在使用过程中不仅受气膜激振力的影响,还受到来自叶轮转子系统、轴承系统的影响,为了保证机械设备的可靠运行,研究轴系振动、轴承油膜力等因素对干气密封系统的稳定性显得尤为重要.李松涛等[1]以迷宫密封-滑动轴承-转子系统为研究对象,采用Muszynska非线性力学模型对迷宫密封在不平衡量激励下的非线性动力稳定性进行分析,并利用Floquet理论分析了系统失稳后的非线性动力学行为.徐华等[2]以机械密封转子轴承系统为研究对象,建立了考虑机械密封影响的转子轴承系统动力学理论模型,分析不平衡激励下考虑机械密封系统时转子轴承系统的强迫振动响应规律以及密封结构参数对系统稳定性的影响.李永[3]以迷宫密封转子系统为研究对象,综合分析了轴承油膜力、流体激振力、碰撞、干摩擦等因素对转子系统运动特性的影响.沈小要[4]以超超临界大型汽轮发电机组为研究对象,分析由转子质量不平衡和油膜涡动和油膜振荡等因素对转子系统发生弯扭耦合振动问题,研究表明随着气体压力的升高系统的失稳转速减小,增加了转子系统失稳的可能性.王晓艳[5]以转子-轴承-密封系统为研究对象,建立多齿Muszynska密封力和非线性油膜力共同作用下的转子-轴承-迷宫密封系统的动力学模型,探寻在多齿密封力和非线性轴承油膜力共同作用下密封系统内部流场变化规律及其非线性动力学特性.刘焰明等[6]以转子-轴承-密封耦合系统为研究对象,采用数值积分方法分析了系统的非线性动力学特性.崔颖等[7]以大型汽轮机转子-密封-轴承系统为研究对象,综合分析了密封的非线性激振力、可倾瓦轴承的弹性支承力、转子阻尼力、不平衡质量力和重力等因素以及系统结构参数对转子不平衡响应和稳定性的影响.张万福等[8]以转子-轴承-密封系统为研究对象,建立轴承-密封耦合作用下的系统有限元模型,并对轴承、密封动力特性系数进行分析求解,研究表明密封流体激振力的存在促进轴承内油膜失稳故障发生,影响转子-轴承-密封系统的稳定性.丁雪兴等[9]以气膜-干气密封环为研究对象,在双自由度系统轴向振动理论基础上推导干气密封动、静环振动振幅的解析式,探寻系统的轴向振动响应规律.张伟政等[10]以叶轮转子-轴承-干气密封系统为研究对象,利用ANSYS软件建立有限元模型,对比分析满载和空载下系统的各阶固有频率和振型的变化规律,通过谐响应分析得到以系统不平衡量为体载荷系统的稳态不平衡响应曲线.张伟政等[11]以转子-轴承-干气密封系统为研究对象,建立转子-轴承-干气密封系统轴向振动动力学模型,定性分析干气密封螺旋角及槽深等结构参数对系统稳定性的影响.薛建雄[12]以转子-轴承-干气密封系统为研究对象,建立系统振动力学模型以及双自由度系统振动方程,推导得出干气密封气膜轴向刚度和阻尼及角向刚度和阻尼的解析式,并通过搭建转子-轴承-干气密封系统实验台,对不同槽深下干气密封静环振动与阻尼进行了测试分析.吴传扬[13]以转子-轴承-干气密封为研究对象,探寻干气密封静环振动最优的螺旋槽角度并分析失稳临界点角度下的混沌现象.目前,国内外学者对转子-轴承-干气密封系统非线性动力学研究已取得丰硕成果,其非线性动力学理论基础也日益完善,但对特殊工况和不同密封槽型结构参数下转子-轴承-干气密封系统稳定性的影响仍有待进一步研究.
本文以转子-轴承-干气密封系统为研究对象,综合考虑轴承油膜力及外界瞬时激振力对干气密封系统稳定性的影响,建立转子-轴承-干气密封系统轴向振动模型,对密封系统添加轴向瞬时扰动,并利用近似解析法求解微尺度下的非线性雷诺方程,利用复函数和迭代法对干气密封气膜边值问题进行推导得出气膜轴向刚度及轴向阻尼的表达式,将系统工况参数及干气密封槽型结构参数代入解析式进行拟合,推导干气密封不同槽数下的气膜刚度及气膜阻尼表达式并编程计算.通过分析时间历程图和相轨图探寻系统轴向振动特性最优螺旋槽数范围,对比分析不考虑外界扰动的干气密封静环-气膜系统和转子-轴承-干气密封系统在实际工况下干气密封槽型参数的稳定范围,探寻受油膜振动等任意单向扰动对干气密封系统轴向稳定性的影响规律,为干气密封非线性稳定性研究及设计提供理论指导.
1 静环-气膜系统轴向振动研究
依据干气密封非线性动力学构建静环-气膜系统理论模型,建立静环-气膜轴向振动模型,通过耦合求解静环-气膜振动方程分析在不同槽数响应下干气密封系统的稳定性,确定干气密封稳定性最优的槽数范围,为进一步分析转子-轴承-干气密封系统非线性动力稳定性提供理论基础.
1.1 静环-气膜系统轴向振动模型
为简化静环-气膜系统轴向振动模型,需做以下假设条件:
1) 干气密封动环和静环只沿轴向做振动运动,不受角向扰动;
2) 干气密封气膜轴向振动模型简化为单自由度受迫振动;
3) 干气密封系统气膜简化为具有非线性阻尼和刚度的弹簧;
4) 假设外部瞬时扰动力为简谐激振力,静环轴向振动简化为简谐运动.
假定干气密封系统密封压力相对稳定,动静环端面间不存在接触,气膜-静环系统轴向振动基本方程:
m2x″+C2x′+K2x+K3x=F(t)
(1)
式中:K3为弹簧刚度;K2为气膜刚度;C2为气膜阻尼;m2静环质量;x为静环振动位移;F(t)表示作用在离散质量上的力,其大小为
Fi(t)=Pisin(ΩT+τ)
以干气密封静环作为振子,建立气膜-静环系统轴向振动模型如图1所示.
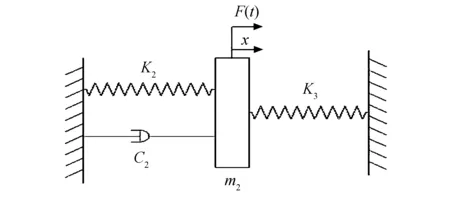
图1 气膜-静环系统轴向振动模型Fig.1 Axial vibration model of gas-static ring system
1.2 气膜刚度和阻尼表达式推导
利用近似解析法求解微尺度下的非线性雷诺方程,利用复函数和迭代法对干气密封气膜边值问题进行推导[14]得到气体压力函数表达式.给静环-气膜系统添加轴向扰动,得到干气密封气膜轴向反作用力的压力增量;利用复数和迭代法对气膜边值问题进行求解,推导出气膜轴向刚度以及轴向阻尼的解析解.
气膜推力表达式:
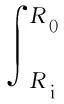
(2)
无量纲化
(3)
定义轴向刚度:
由微扰动态压力下复数实部Re{K}=η(η1cosω+η2sinω)推导无量纲轴向气膜刚度:
(6)
系统的轴向气膜刚度:
(7)
由压力的复数虚部:Im{K}=η(-η1sinω+η2cosω)推导无量纲轴向气膜阻尼系数表达式:
(8)
轴向气膜阻尼表达式:
(9)
1.3 特例计算
特殊工况下(转速为16 500 r/min)静环-气膜密封系统的几何运行参数见表1所列.

表1 静环-气膜密封系统运行参数
将工况参数及干气密封槽型结构参数代入轴向气膜刚度及气膜阻尼表达式进行拟合,并通过编程计算获得了静环-气膜系统气膜刚度、振动位移与槽数的三维关系曲面如图2所示.
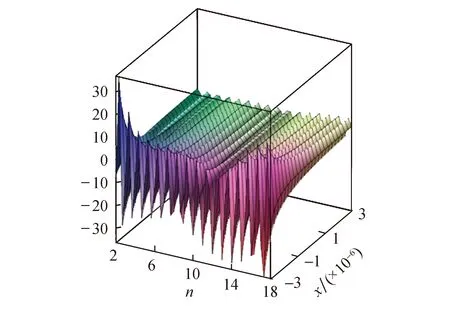
图2 Kg随n、x的变化曲面Fig.2 Surface of Kg varying with n and x
通过分析图2得出:随着螺旋槽槽数的增加,气膜刚度也随之增大,且干气密封螺旋槽槽数为12、13、14时干气密封气膜刚度最大.为验证该特殊工况下最大气膜刚度在槽数为12到14处,将气膜-静环系统数据带入式(7),步长为0.000 01拟合出不同螺旋槽槽数下气膜刚度和气膜阻尼表达式.
螺旋槽数n=8,系统气膜刚度与气膜阻尼拟合表达式(10,11),在x=0处的气膜刚度为Kg=-1.54 N/μm,气膜阻尼为Cg=0.97 N·s/μm.
Kg=(2.305 010 000×1016n-
1.883 346 101×1017)x3+
(5.162 465 000×1011n-
4.216 255 252×1012)x2+
(3.854 070 000×106n-
3.146 310 136×107)x+
9.590 950 000n-78.262 801 65
(10)
Cg=(1.274 425 000×1016n-
9.917 839 712×1016)x3+
(2.859 455 000×1011n-
2.228 758 336×1012)x2+
(2.138 590 000×106n-
1.669 480 679×107)x+
5.331 580 000n-41.685 155 21
(11)
螺旋槽数n=12,系统气膜刚度与气膜阻尼拟合表达式(12,13),x=0处气膜刚度为Kg=-2.80 N/μm,气膜阻尼为Cg=-1.19 N·s/μm.
Kg=(-1.870 050 000×1015n+
1.484 719 123×1016)x3+
(-8.147 000 000×1010n+
8.248 165 806×1011)x2+
(-609 050.0n+
6.176 246 184×106)x-
1.517 950 000n+15.418 839 45
(12)
Cg=(3.166 185 000×1016n-
3.825 022 572×1017)x3+
(7.097 590 000×1011n-
8.576 720 152×1012)x2+
(5.303 520 000×106n-
6.410 428 508×107)x+
13.209 800 00n-159.709 780 6
(13)
通过推导拟合得出不同螺旋槽槽数下的气膜刚度和气膜阻尼表达式,与气膜-静环系统的轴向振动方程(1)联立求解,利用四阶Runge-Kutta法对气膜-静环系统轴向振动方程进行编程求解,获得干气密封气膜-静环系统不同螺旋槽数响应下的时间历程图和相轨图,如图3所示.

图3 不同螺旋槽槽数下的时间历程图和相轨图
为探究不同螺旋槽槽数下静环-气膜系统静环的最大振幅变化规律,选取螺旋槽槽数从6到16的范围进行参数化分析,分析不同螺旋槽数响应下时间历程图和相轨图得出静环振动的最大振幅,在特殊工况下静环的最大振幅随着螺旋槽槽数的变化曲线如图4所示.

图4 静环最大振动振幅随螺旋槽槽数变化曲线Fig.4 Variation curve of maximum vibration amplitude of static ring with the number of spiral grooves
在特殊工况下,螺旋槽槽数对静环-气膜系统静环振动的最大振幅影响不大,振幅最大差值约3 μm.在槽数变化范围从6到10和从14到16内,槽数的变化引起最大振幅较大的变化,在槽数为10~14范围内,静环最大振幅基本在1.5 μm左右.实际工况下,因为螺旋槽槽数的变化,干气密封系统形成的动、静压效应不同.当螺旋槽数较少时密封环槽宽比小,升力垫作用不够;随着槽数增多干气密封系统静环最大振动振幅急剧升高,此时动静环追随性变差,干气密封系统稳定性较差,导致密封坝工作面密封性能变差.对比分析各槽数响应下时间历程图和相轨图可知,螺旋槽槽数范围为10到14时,单自由度静环-气膜系统中干气密封气膜刚度较大且动静环追随性较好,此时干气密封系统稳定性最优.
2 转子-轴承-干气密封系统轴向振动研究
转子-轴承-干气密封系统中轴承与轴之间为油膜润滑,当系统受到外界任意单向干扰时,油膜振动产生的瞬时激振力会影响干气密封气膜稳定性,当外界干扰引起密封端面气膜的变化很大时会导致干气密封动静环发生碰撞从而导致密封失效.故以转子-轴承-干气密封系统为研究对象,将转子轴承简化成一个带有阻尼的弹簧建立系统轴向振动模型,分析转子-轴承-干气密封系统下螺旋槽槽数对于干气密封静环振动幅值的影响,为干气密封系统稳定性分析提供理论依据.
2.1 转子-轴承-干气密封系统轴向振动模型
转子-轴承-干气密封系统轴向振动模型假设:
1) 干气密封端面平行,气膜流动截面不变;
2) 忽略旋转效应,不计气体质量力;
3) 将转子-轴承系统简化为非线性阻尼弹簧;
4) 将干气密封系统气膜视为具有非线性阻尼和刚度的弹簧;
5) 将转子-轴承-干气密封系统视为双自由度受迫振动系统;
6) 轴系瞬态激振力假定为简谐激振力,其轴向位移假定为简谐运动.
建立转子-轴承-干气密封系统轴向振动模型如图5所示.
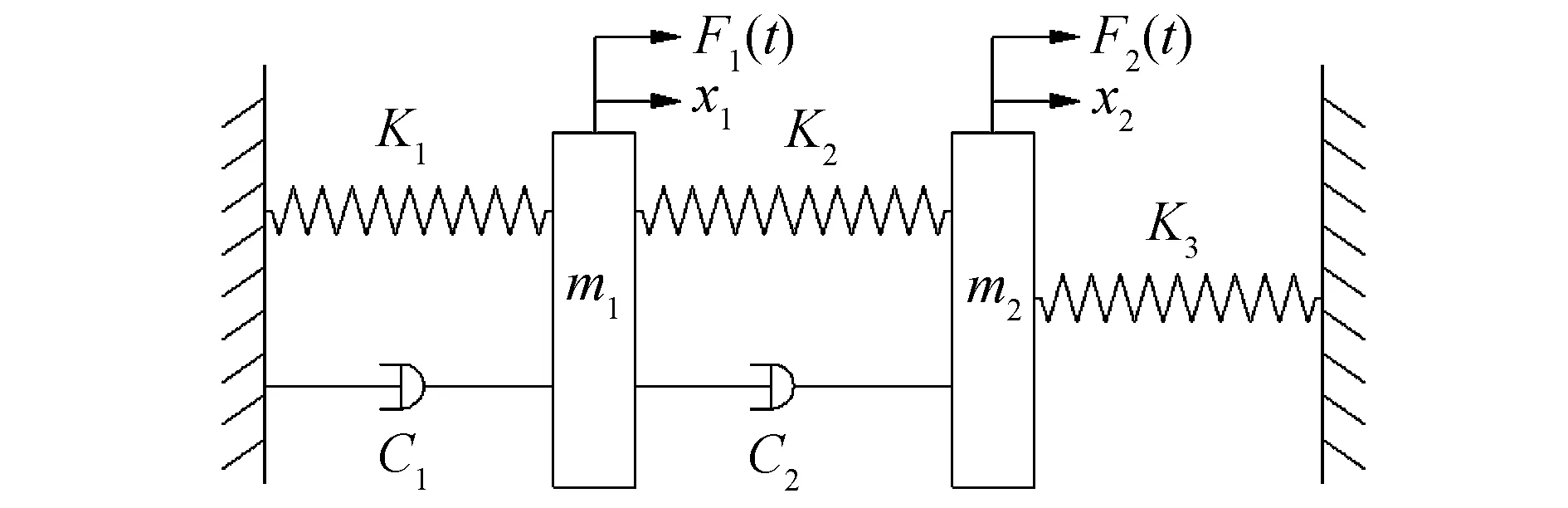
图5 转子-轴承-干气密封系统轴向振动模型Fig.5 Axial vibration model of rotor-bearing-dry gas seal system
其中:m1为轴系和干气密封动环的总质量;K1为轴承刚度;C1轴承阻尼;x1为动环的振动位移;m2为干气密封静环的质量;K2为气膜刚度;C2为气膜阻尼;x2为静环的振动位移;K3为弹簧刚度;F1(t)和F2(t)为简谐激振力,其大小为Fi(t)=Pisin(ΩT+τ)
2.2 转子-轴承-干气密封系统轴向振动分析
根据转子-轴承-干气密封系统轴向振动模型列出系统离散质量运动方程:
(14)
引入无量纲变量:
代入式(15),整理得
(15)
令Y1=X′1,则Y′1=X″1;Y2=X′2,则Y′2=X″2,降阶化处理式(16):
(16)
为探究干气密封不同槽数下转子-轴承-干气密封系统稳定性,选取螺旋槽槽数从8到16的范围进行参数化分析,分析不同螺旋槽数响应下时间历程图和相轨图得出静环振动的最大振幅,将干气密封不同螺旋槽槽数下的参数μk,2,μc分别代入到式(16),利用四阶Runge-Kutta法对双自由度振动方程进行推导求解,利用Maple软件编程求解得出不同螺旋槽槽数响应下的时间历程图和相轨图如图6和图7所示.

图6 不同螺旋槽槽数下的时间历程图

图7 不同螺旋槽槽数下的相轨图Fig.7 Time phase orbit diagram of different spiral groove number
分析特定工况下不同螺旋槽槽数响应下的时间历程图和相轨图可知,当转子-轴承-干气密封系统受到外部瞬时扰动及油膜激振力的影响,双自由度振动系统静环振动的最大振幅均为20μm左右,且最大振幅明显大于不考虑转子-轴承系统振动的单自由度气膜-静环系统静环的振动幅值,进一步说明转子-轴承对干气密封稳定性的影响不可忽略.通过分析不同螺旋槽数响应下时间历程图和相轨图可知,随着干气密封螺旋槽槽数的变化,尽管双自由度振动系统静环振动的最大振幅远远大于干气密封气膜厚度,但由于干气密封动静环追随性较好,干气密封并未失效.
3 结论
1) 单自由度静环-气膜系统中,随着螺旋槽槽数的增加干气密封气膜刚度不断增强.在螺旋槽槽数为12时气膜刚度最大,静环-气膜系统静环最大振幅最小,干气密封稳定性最优.
2) 对比单自由度静环-气膜系统可知,在双自由度模型系统中,由于静环振动不仅受到静环本身以及气膜刚度的影响,还受到转子-轴承的振动影响,转子-轴承-干气密封系统在相同工况条件及槽型参数下静环振动位移大于单自由度静环-气膜系统静环振动位移,特定工况下,螺旋槽槽数的变化对于转子-轴承-干气密封系统中的静环振动最大振幅影响较小,静环最大振幅均为20 μm.
3) 转子-轴承-干气密封系统在实际工况下干气密封槽数的稳定范围为10到14,该槽数范围内气膜刚度较大,动、静环追随性较好,密封性能好,对干气密封槽型参数优化设计及稳定性分析提供理论指导.
