线性代数知识点的可视化教学设计探索与实践

李清华， 王宝娟

(烟台大学 数学与信息科学学院，山东 烟台264005)

1 引 言

“新工科(Emerging Engineering Education)”以培养多元化、创新性卓越工程人才为主要目标，对教学方式提出了新要求.工科的线性代数教学不仅要紧密结合产业背景和专业特点，更重要的是激发学生学习和探究的兴趣，强化教师的引导，体现学生学习的主体地位，实现以产出为导向的OBE(Outcomes-based Education)教学改革[1].传统课堂教学面临多重挑战：一方面多数线性代数教学方式难以充分调动学习兴趣，教学方式难以跳出理论抽象性的掣肘，对于产业应用案例引入较少，授课内容缺乏生动性，信息化辅助教学方式单一，使得讲授内容没有完全激发学生的学习兴趣；另一方面，教学内容不能有效结合产业实际情景，例如囿于人工演算局限性，出现矩阵等运算往往不能超过4阶运算的问题，使得学生难以完全理解教学知识点，更难以培养学生线性代数的应用能力.因此，改进传统线性代数教学以适应“新工科”要求成为一个亟待探究的问题.

线性代数的教学内容和教学形式的改革是国内近年研究的重要主题，主要围绕信息技术的运用展开，特别随着互联网技术的加持，混合式课堂环境的支撑，线性代数教学改革探索不断丰富.在教学模式方面，将翻转课堂应用到线性代数的课堂教学中，改变教师角色，组织和引导学生自主学习，促进OBE(Outcomes-based Education)和教学质量的提高[2]；在教学内容方面，针对计算机学院代表的信息类专业对线性代数课堂的教学内容进行改革，突出理论与实践相结合，强化线性代数的学科应用以及加强对编程语言的训练[3-4].其中，研究线性代数教学中的概念可视化处理，可以促进学生具象化学习和提升结合案例的实践能力，成为教学改革研究中有价值的探索领域.目前已有文献中多使用MATLAB等专用软件来处理线性代数中的概念可视化问题，应用领域多集中在矩阵的运算部分.但是学界对计算机编程语言Python编程开发知识点可视化的实践研究较少.本研究聚焦线性代数抽象概念具象化的教学课程改革，引入Python编程语言设计，探究一种促进学生学习主动性与应用能力提升和符合“新工科”要求的教学设计.

2 可视化教学设计的探索与实践

大学生具象思维特征显著，他们更喜欢接受和理解具体形象的知识，而线性代数理论较为抽象，难以充分激发学生的学习兴趣.因此，本研究以“新工科”教学要求，对线性代数的传统课堂模式进行改革，用实例引入理论，以问题为驱动，将线性代数理论进行形象化，使得理性的知识化为感性的实例，调动学生学习的积极性.

Python作为目前人工智能领域中的一门重要编程语言，应用于科学计算、云计算、数据分析、自动化运维等多工业领域，特别在图形界面开发上具有明显优势.同时，Python语言具有简单灵活、扩展性强、开源、免费等特点，只要学生具备计算机应用基础能力，就容易激发兴趣.本研究使用Python语言，将线性代数教学中部分应用非常广泛的内容可视化处理，以当今热议的人脸识别和图像处理应用领域为例，将矩阵的基本运算、特征值与特征向量、奇异值分解三个知识主题相关理论结合，激发学生的兴趣，增强知识应用意识.

教学应用过程分为三个阶段，以适应不同知识需求的学生.课前老师通过混合课堂线上发布课件和Python主要源码；课上老师主要现场演示可视化程序，也可以引导学生分享操作；课后老师布置挑战性的进阶题目，学生修改代码来探索和创新，从而加深知识的理解和应用.

2.1 矩阵的基本操作与图像处理

图像中的每个像素值就是矩阵的每个元素值，可以说，图像可以用矩阵来表示，所以对数字图像的处理实际就是对矩阵的处理.一张彩色图像可以是一个矩阵，只不过此矩阵的每一个点不是单个数值，而是一个3元素的数组，这3个元素是RGB值，R(RED)为红色，G(GREEN)为绿色，B(BLUE)为蓝色，范围为0～255，所以一张彩色图像可以视为3矩阵叠加形成，如图1，其中1个矩阵就是1个通道.灰度图属于单通道图像，像素的灰度值范围为0～255，用来可视化矩阵，如图2是一张512×512的灰度图像，对应一个512×512的矩阵，元素值就是灰度值0～255.

图1

图2

在课堂实际操作中，用数字图像来可视化矩阵，可以帮助学生很好的理解矩阵的基本操作，如加法、减法和数乘等操作[5].学生们可以通过对这些图像矩阵的基本运算，得出最直观的运算结果，从而去巩固和加深矩阵知识.

在python 3.0及以上版本中调用下表中函数时，需要先在python中安装OpenCV模块来使用其中的库函数.具体操作：运行命令提示符(即cmd)，使用‘cd’命令进入python安装路径下的scripts目录中，如C:Program FilesPython35Scripts，然后输入命令：pip3 install opencv-python，加载成功之后，在IDLE中输入import cv2.

2.1.1 矩阵的加法

通过改变图像的亮度可以帮助理解矩阵的加法.在工业情景的实际操作中，改变图像亮度是一种使图像更加符合规范的修复手段，对于图像矩阵图3(a)的每一个元素，加上一样的增量，若增量为正，如100，则亮度提升，如图3(b)所示；反之，增量为负，如-100，则亮度降低，如图3(c)所示.

图3 (a)—(c)原图与加上增量之后对比图

安装OpenCV模块，在Python IDLE中调用函数add_demo实现图像矩阵的加法，格式和说明见表1.

表1 函数add_demo调用和说明表

以上矩阵的加法是在一张图像矩阵的基础上加上一个所有元素都一样的矩阵，可用来调节图片的亮度.两个图像矩阵相加的结果，运行如图3(d)所示.

2.1.2 矩阵的数乘

矩阵的数乘也可以改变图像的对比度：将原图像矩阵乘以一个大于1的数，如1.5，就可以提升图像的对比度；反之，矩阵乘以一个小于1的数，如0.5，就可以降低对比度.如图4所示.

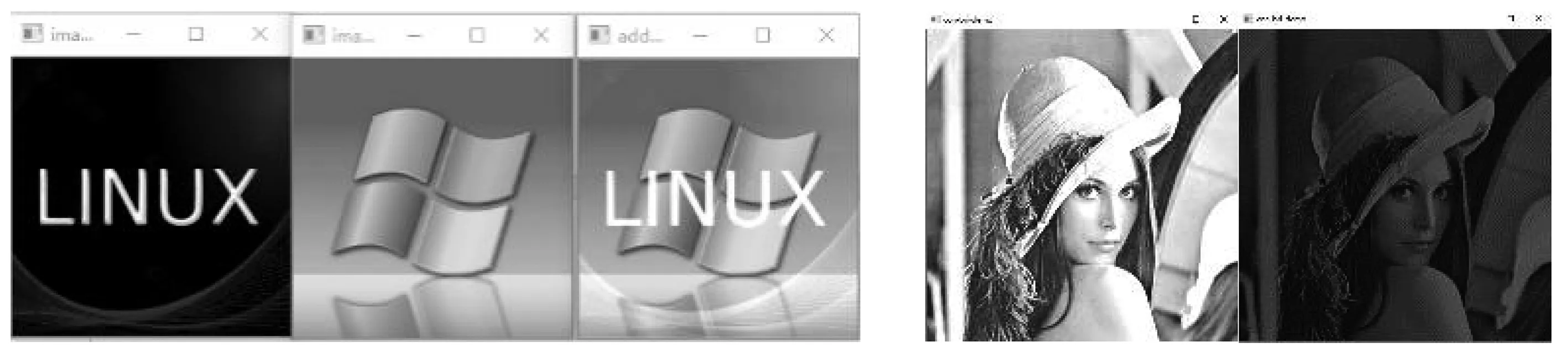
图3(d)两张图像相加的图示 图4 图像对比度改变的图示

调用如下函数实现图像矩阵的对比度的改变，格式见表2.

表2 函数contrast_brightness _demo调用和说明表

在此函数中，改变其中的c值就可以改变图像矩阵的数乘大小从而改变图像对比度；改变其中的b值即相当于给图像矩阵作加法，改变图像亮度.

2.1.3 矩阵的减法

矩阵作差，会收获到图片反转的效果，图5(a)是原矩阵与纯白图像作差.白色图像的矩阵所有元素都为255.部分矩阵的计算演示以及结果如下：

调用函数subtract _demo实现图像矩阵的加法，格式和说明如表3所示.

表3 函数subtract _demo调用和说明表

以上矩阵的减法是元素都一样的矩阵减去一个图像矩阵，可以得到图片反转的效果.下面是两个不一样的图像矩阵相减的结果，如图5(b)所示.

(a) (b)

2.1.4 矩阵的乘法

卷积在信号处理中应用广泛.在人工智能领域中，由卷积层组成的卷积神经网络(Convolutional Neural Network，CNN)是一种非常重要的深度学习研究方法.在图像处理领域中，卷积运算(也称为滤波运算)主要用到了矩阵的乘积和线性运算，具体公式如下：

其中，G是原图像，F是滤波器矩阵(Filter，也称卷积核)，H为滤波之后的图像.直白了说，卷积和加减乘除一样，也是一种运算，其根本操作是将两个矩阵的其中一个先平移，然后再与另一个矩阵相乘后的累加和.

在实际应用中，锐化、模糊和边缘的滤波器卷积矩阵最常用[6]，具体分别是

调用OpenCV库函数cv2.filter2D，格式与说明见表4.

(1)绞车由1台功率300 kW的交流变频电机驱动，减速箱设有两挡，手动换挡，可实现挡内无级调速，并通过换挡实现较大扭矩或较大转速。可以实现在高速挡时绞车输出较高转速和较大的提升力，满足快速提下钻要求，节约辅助作业时间，提高效率；在处理孔内事故或超深孔钻进时，可选择低速挡，绞车输出大扭矩和较低转速，实现以较小功率满足不同工况各种作业要求。绞车变速范围大，提升能力强。

表4 函数cv2.filter2D调用和说明表

三种滤波器其对应的处理效果见图6.在教学中，老师可以引导学生独立设计多个滤波器矩阵，改变kernel的值，输出原图像的卷积后的结果图，加强对矩阵乘法的理解.

图6 滤波器的锐化、模糊以及浮雕效果图示

图像的旋转也可以理解为矩阵的乘法或者线性变换，其原理见图7，把点A移动到点B，可以用如下公式表示这个旋转过程：

图7 坐标旋转示意图 图8 图像旋转图示

调用函数srotate实现简单的图像旋转，运行效果如图8所示，调用函数格式和说明见表5.

表5 函数srotate调用和说明表

在教学中，可以让学生课下尝试改变其中旋转角度angle，计算矩阵乘法，然后运行程序，深刻地理解旋转中的矩阵乘法原理.

2.2 特征值与特征向量和人脸识别

特征值和特征向量是线性代数中的重要概念，有着很强的应用背景，广泛应用于计算机视觉和图像处理、数据挖掘等研究领域中.特征脸法是一种比较典型的人脸识别算法，其核心是PCA，也就是主成分分析方法.众所周知，图像、文本等非结构化数据都是很高维度的，直接对这些高维数据操作将非常困难，也很难提取典型特征.PCA是一种线性降维算法，基本原则是将高维矩阵特征通过投影矩阵线性变换得到低维矩阵特征，是人脸识别和图像重构常用技术之一[7].一个矩阵A的特征向量就是经过线性变换y=Ax之后，向量方向保持不变，只发生了伸缩和变形，其伸缩的比例就是特征值[8].

在特征脸法中，将输入的人脸图像向量经过一系列处理和计算得到一个协方差矩阵，计算这个矩阵的特征值和特征向量，得到的这些特征向量就可以看作一个图像，即特征脸，实际就是一些脸部的特征.这些特征脸是特征子空间的一组基，对训练集的每一张人脸来说，都是这些特征脸的线性组合[9]，如图9所示.通过特征脸将输入图片向量化，得到特征向量，然后对比此向量与样本库中人脸向量的欧氏距离，依据给定阈值判断是否属于同一个人.

图9 通过特征脸权重来代表人脸图片的特征

通过10轮交叉验证特征脸法在ORL人脸库上的识别精度.此库包含40个不同人的400张图像，所有图像都是灰度图并且以BMP格式存储.将数据集的部分人脸用来训练模型，选取小部分用来测试，以此验证此方法的精度.

表6 函数调用格式和说明表

部分人脸数据集和运行效果如图10所示.

图10 从左到右依次为：ORL部分人脸数据集、平均脸、识别结果

通过这10次的交叉验证，最后得到的验证准确度为96.5%，为较好水平，即通过少量的样本可以得到不错的结果，说明此法能较好地保留主要特征，在图像降维上有不错的结果.

在教学中，教师推送相关资料，学生自己建一个人脸数据库或者使用已建好的人脸数据集，调整image的数据或者验证次数，查看平均特征脸以及识别结果.学生根据运行结果试验此方法的准确度，感受识别过程中的数学原理，从而更好地理解特征值和特征向量的实际作用与意义.

2.3 奇异值分解与图像压缩

为了高效存储和传输图像数据，工业上常用图像压缩技术来减少图像的多余信息.数字图像压缩是通过减少图像矩阵的数据量，用较少的量来还原原来图像的一门技术.使用矩阵的分解获得图像矩阵的前k个特征值进行恢复该图像，在k值取的得当的情况下，图像的品质不会受太大损失，却大大节省了存储空间.

在实际中，图像矩阵一般都不是方阵，所以相比特征值分解，奇异值分解有着更广泛的应用.奇异值分解可以把矩阵分解为多个秩为1的矩阵之和[10]，形如：

其中的σ就是奇异值，u和v分别表示列向量.等式右边的每一项uvT都是秩为1的矩阵.

把奇异值按照σ1≥σ2≥…≥σr排列，留下相对大的奇异值，去除小的奇异值，来近似描述图像矩阵.在实际操作中，前10%甚至1%的奇异值之和可以占全部的99%.因此矩阵可以用最大的k个奇异值与对应向量来近似代表，即：

调用Numpy库函数和svd_restore函数，可以将一张灰度图进行奇异值分解，然后输出保留不同奇异值个数的图像，对比所占存储空间大小和输出效果，如图11所示，第一张为原图，其余为分别保留1，5，10，20，50，100，150个奇异值之后复原的图像.

图11 原图与复原后的图像对比示意图

调用函数格式和说明见表7.

表7 函数调用格式和说明表

由输出的图像信息可得，原图尺寸为512×512，保存这张图需要存储512*512=262144个像素点，有26万之多，在计算机中实际占空间为160KB.这张图有512个奇异值，将他们从小到大排序之后，排在最后的较小的奇异值对整张图片贡献不大，故可以舍去.由输出图可以明显看出，仅保留前20个奇异值就可以清晰看到人脸特征，但是显然不够清楚.如果选择保留前50个奇异值，图片占用存储空间会稍微大一点但清晰度会上升.此时图片有50*(1+512+512)=51250个像素点，仅为原来图片像素点个数的19.6%，在实际文件保存中，所占存储空间为120KB，为原图的75%.因此可以看出，奇异值分解可以在保留原图主要特征的基础上对图像压缩，节省了很多存储空间.

在教学中，教师引导学生课下在实际演练中更换自己的图片和奇异值个数，对自己的图像进行压缩，充分理解奇异值分解的过程和意义，加深知识的理解.

3 教学效果

本研究在部分班级采用了知识点的可视化教学，内容包括但不限于矩阵的基本运算、特征值与特征向量、奇异值分解.教学效果显示，相比于其他并行的传统教学课堂，实施教学改革的课堂学生学习效率更高，学生平均成绩最高，如图12所示.其中高分段学生显著更多，不及格人数是最少的.此外，在学习体验方面，学生们对教师课堂评价的百分位，从2017年的30.14%(改革前)增长到2019年的59.33%(改革后)，也说明改革后的课堂能更受欢迎，学生参与度更高，从而课堂效率更高.

图12 三种教学模式下的学生成绩对比(灰度等级最高的为改革后的教学课堂)

囿于研究投入和部分理论抽象的天然性，Python等语言和软件的应用无法展示全部的线性代数内容，也不能完全取代理论讲解的主导地位，但是这种可视化的教学设计一定程度上可以帮助学生在课中或者课后更好地理解知识内容.

4 结 论

本研究利用Python实现对线性代数部分理论概念的可视化，将抽象的知识具象为感性的应用实例，激发学生的学习兴趣，提高课堂的教学效率.可视化突出了线性代数在人脸识别以及图像处理领域中的实际应用，课堂中引入概念可视化能够适应学生们的不同学习基础，尊重他们不同的学习动机，满足学生及时反馈和课堂讨论的需求.学生在实际操作中，不仅能够掌握理论上的知识，也能更深入地接触社会中的实际应用，有利于提高他们的科学素养，提高社会责任感.知识点可视化是线性代数教学改革中具有价值和意义的探索和实践.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.