无色散p-约化KP系列的弦方程

2022-05-07虎蓉，易戈

大学数学 2022年2期

虎蓉，易戈

(合肥工业大学数学学院，合肥230601)

1 引言

在可积系统领域中，Kadomtsev-Petviashvili(KP)系列是非常重要的一个研究课题，它具有许多良好的结构.弦方程的研究在KP系列的理论发展中起着重要的作用.Orlov和Schulman通过定义一个拟微分算子M得到附加对称流的具体形式，这些附加对称流构成一个无中心的W1+∞代数[1].特别地，Dickey研究了 KP系列的附加对称、弦方程和Virasoro约束等物理问题之间的联系，并且，利用Lax算子L和附加对称算子M给出了附加对称对KP系列τ函数的作用[2-3].约束离散KP系列及量子化推广KP系列也已被研究[4-6].Panda和Roy研究了p-约化KP系列τ函数的Virasoro代数约束[7].

无色散可积系列在数学物理的许多领域具有重要的意义，在数学物理的诸多方面都有应用.Krichever给出了的无色散Lax方程[8]，这为无色散KP系列的后续研究奠定了基础.后来，Takasaki和Takabe对无色散KP系列的研究做出了较大贡献，他们讨论了该系列的Lax表示、无穷多对称、无穷多守恒量、附加对称和twistor结构等[9-10].虽然无色散KP系列已经进行过许多研究，但其弦方程一直未被明确给出，这便是本文的研究动机.论文给出了无色散KP系列的弦方程，并在此基础上又给出无色散p-约化KP系列的弦方程.

2 预备知识

无色散KP系列[9]的Lax函数L定义为关于k的形式劳伦级数

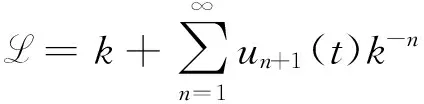
满足下面的Lax方程

(1)

其中，Bn=(Ln)≥0，n=1，2，….泊松括号的定义为

引理1[9]存在dressing算子eadφ使得无色散KP系列的Lax函数可表示为dressing形式

L=eadφ(k)，

且满足等式

∇tn，φφ=-(eadφ(kn))≤-1，n=1，2，….

(2)

其中

定义1[9]无色散KP系列的Orlov函数M由dressing算子eadφ定义

(3)

(4)

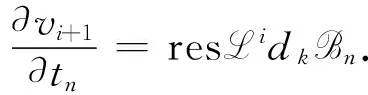
引理2[9]无色散KP系列的Orlov函数M满足Lax方程

(5)

且满足正交关系式

{L，M}=1.

(6)

3 无色散p-约化KP系列的弦方程

命题1由无色散KP系列的两个函数L和M满足正交关系(6)可以推出以下等式成立：

{Ln，ML1-n}=n.

(7)

证由等式{L，M}=1，结合泊松括号的运算性质，易得下式成立：{Ln，M}=nLn-1.接着，由莱布尼兹规则可得

{Ln，ML-n+1}={Ln，M}L-n+1+{Ln，L-n+1}M={Ln，M}L-n+1=n.

(8)

称等式(8)为无色散KP系列的弦方程.

至此，无色散KP系列的弦方程已被给出，下面考虑约化情形下的弦方程.对无色散KP系列的Lax算子增加约化条件：(Lp)≤-1=0，p≥2，称之为无色散p-约化KP系列，其Lax函数Lp=kp+up-2kp-2+…+u0满足：

定理2对于无色散p-约化KP系列有下列等式成立：

且满足弦方程

(9)

证根据函数M的表达式(4)可得

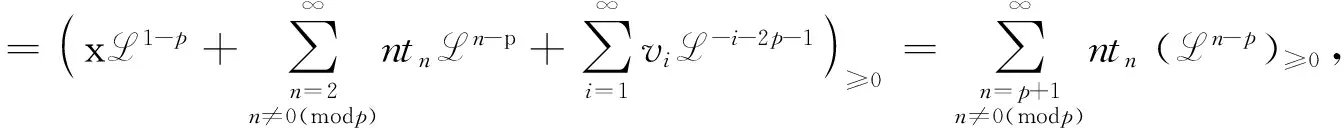
则由等式(8)可得

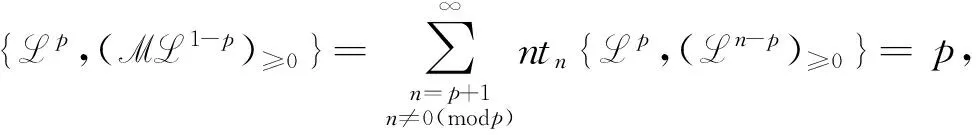
即弦方程(9)成立.

上述定理表明，对于无色散KP系列的Lax函数L及其对应的M，若满足弦方程(8)，则该系列一定是无色散p-约化KP系列；反之，无色散p-约化KP系列的Lax函数L及其对应的函数M一定满足弦方程(9).

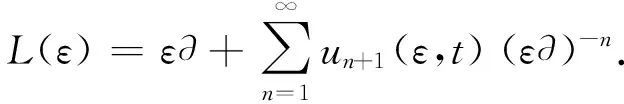
定义3拟微分算子的“order”为

由此定义拟微分算子的“principal symbol”为

基于上述定义，可知无色散KP系列的解与KP系列的解有如下关系[9]：L=σε(L(ε))，且M=σε(M(ε))就是与之对应的Orlov函数.给出的无色散p-约化KP系列的弦方程(9)与p-约化KP系列的弦方程也保持着这样的对应关系，即原来关于∂的拟微分算子对应着关于k的形式劳伦级数，原来的李括号就对应着无色散情形下的泊松括号.