一类丢番图方程与有限域上对角方程的解

肖义丽， 曹 炜， 胡双年

(1.宁波大学 数学与统计学院，浙江 宁波315211； 2.闽南师范大学 数学与统计学院，福建 漳州363000；3.南阳理工学院 数理学院，河南 南阳473004)

1 引 言

(1)

wi=gcd(wi，lcm[wj:j≠i])， 1≤i≤n，

即w不可能再被压缩.

1949年，华罗庚、Vandiver[5]和Weil[6]分别独立地得到了Nq(f)用特征和表示的公式:

并且得到了下面的定理.

定理1[5-6]设f是形如(1)的多项式，则

|Nq(f)-qn-1|≤I(d1，…，dn)(q-1)q(n-2)/2，

其中I(d1，…，dn)表示下列丢番图方程(u1，…，un)的个数

1986年，孙琦、万大庆和马德刚[7]利用容斥原理给出I(d1，…，dn)的复杂表达式

1987年，孙琦和万大庆[8]得到了I(d1，…，dn)=0的充分必要条件.

1988年，万大庆[9]利用高斯和的Stickelberger定理，推广了Ax[10]和Joly[11]的结论，得到了下面的定理.

定理2[9]设f是形如(1)的多项式，则

Nq(f)≡0(modqL(d1，…，dn)-1)，

其中I(d1，…，dn)>0时，

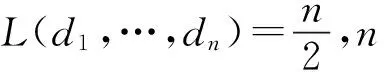
1996年，孙琦[13]证明了以下结论:

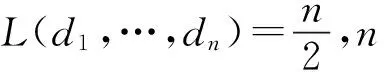
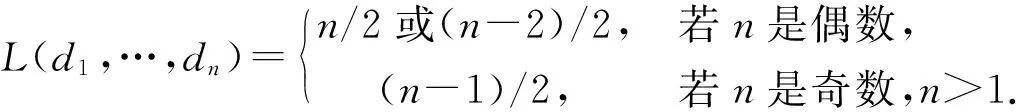
1996年，孙琦[14]证明了以下结论:

(i)I(d1，…，dn)=5，6，7或9时，L(d1，…，dn)=[n/2]，其中[x]表示不超过x的最大整数;

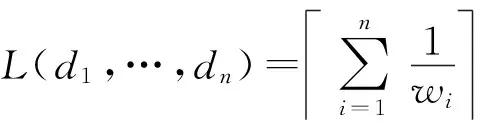
L(d1,…,dn)=∑ni=11wi

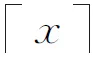
2007年，曹炜和孙琦[16]利用GCD-连通集简化了I(d1，…，dn)，L(d1，…，dn)与Nq(f)的计算.

将给出当I(d1，…，dn)=11，…，18时，L(d1，…，dn)的值，并推广得到当I(d1，…，dn)=p时，其中p为素数，L(d1，…，dn)的值. 还将补充参考文献[11]中当I(d1，…，dn)=6，8，10时，w1，…，wn的具体值.

2 引 理

首先，叙述关于I(d1，…，dn)和L(d1，…，dn)的缩减公式.

引理1[4]设wi=gcd(di，lcm[dj:j≠i])，i=1，…，n，则有

I(d1，…，dn)=I(w1，…，wn)，wi=gcd(wi，lcm[wj:j≠i]).

引理2[13]设wi=gcd(di，lcm[dj:j≠i])，i=1，…，n，则有

L(d1，…，dn)=L(w1，…，wn).

令w表示集合{w1，…，wn}，若w中出现偶数个2，将略去不写出来. 关于下面引理的证明，可以用参考文献[17]的方法来证.

引理3(i)I(d1，…，dn)=6当且仅当w={7，7}，{2，7，14}，{2，8，8}，{2，8，16}，{3，4，12}，{4，4，4}，{4，4，16}，{2，3，4，12}，{2，3，4，24}，{2，3，8，12}，{3，3，3，3}，{3，3，4，4}，{3，3，3，4，4}，{3，3，4，4，9};

(ii)I(d1，…，dn)=8当且仅当w={9，9}，{2，9，18}，{2，10，10}，{2，10，20}，{3，5，15}，{3，6，6}，{2，3，5，30}，{2，3，6，6}，{2，3，9，12}，{3，3，5，5}，{2，3，3，3，6}，{2，3，3，5，10}，{2，3，5，5，6}，{2，4，4，5，5}，{2，4，5，5，8}，{3，3，3，5，5}，{3，3，5，5，9}，{2，3，3，3，5，10};

(iii)I(d1，…，dn)=10当且仅当w={11，11}，{2，11，22}，{2，12，12}，{2，3，10，15}，{3，4，4，6}，{3，4，6，8}，{2，3，3，4，12}，{2，3，4，4，6}，{2，3，4，6，8}，{2，3，4，6，16}，{2，3，3，4，24}，{3，3，3，3，3};

(iv)I(d1，…，dn)=11当且仅当w={12，12};

(v)I(d1，…，dn)=12当且仅当w={13，13}，{2，13，26}，{2，14，14}，{3，7，21}，{4，5，20}，{5，5，25}，{2，4，5，20}，{2，5，6，15}，{3，4，9，12}，{2，4，7，7，8}，{3，3，7，7，9}，{2，3，3，7，9，14}，{2，3，3，8，9，16};

(vi)I(d1，…，dn)=13当且仅当w={14，14};

(vii)I(d1，…，dn)=14当且仅当w={15，15}，{2，15，30}，{2，16，16}，{2，16，32}，{3，8，24}，{4，6，12}，{4，6，24}，{2，3，8，24}，{3，3，4，4，18};

(viii)I(d1，…，dn)=15当且仅当w={16，16}，{2，4，6，12}，{2，4，6，24}，{2，6，12，16};

(ix)I(d1，…，dn)=16当且仅当w={17，17}，{2，18，18}，{2，5，5，10}，{2，5，10，25}，{3，5，6，10}，{3，5，9，15}，{2，3，5，6，10}，{2，3，5，6，20}，{2，3，5，9，30}，{2，3，5，10，12}，{3，4，5，9，30}，{2，3，3，5，5，18}，{2，3，4，5，9，30};

(x)I(d1，…，dn)=17当且仅当w={18，18};

(xi)I(d1，…，dn)=18当且仅当w={19，19}，{2，20，20}，{3，10，30}，{4，7，28}，{4，8，32}，{2，3，10，30}，{2，3，20，30}，{2，4，7，28}，{3，4，4，24}，{3，4，12，16}，{3，5，6，10}，{2，3，4，4，24}.

3 主要结论及其证明

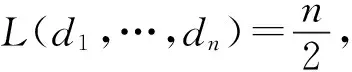
(iii)当I(d1，…，dn)=12,14,16或18时，

证设I(d1，…，dn)=11，由引理3(iv)可知w={12,12}，写成一般形式，即

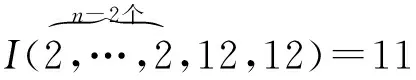
有

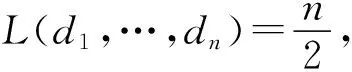
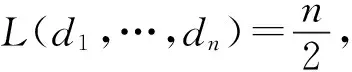
设I(d1，…，dn)=15，由引理3(viii)知当且仅当w为{16,16}，{2,4,6,12},{2,4,6,24},{2，6，12，16}之一，写成一般形式，即

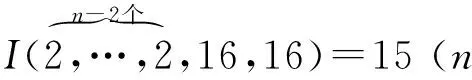
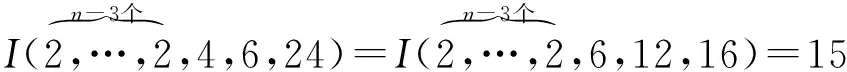
有

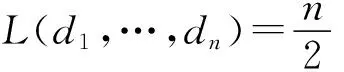
设I(d1，…，dn)=12，由引理3(v)知当且仅当w为{13，13}，{2，13，26}，{2，14，14}，{3，7，21}，{4，5，20}，{5，5，25}，{2，4，5，20}，{2，5，6，15}，{3，4，9，12}，{2，4，7，7，8}，{3，3，7，7，9}，{2，3，3，7，9，14}，{2，3，3，8，9，16}之一时，有

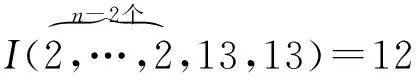
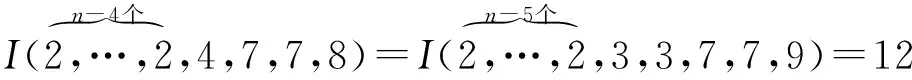
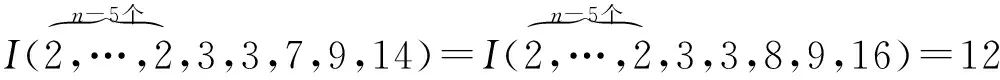
有

再由引理2知，当I(d1，…，dn)=12时，

同理，可证当I(d1，…，dn)=14，16或18时，

这便证明了(iii).

由定理3容易得到下面的推论.

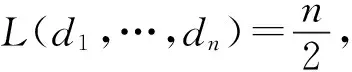
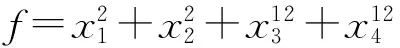
d1=2，d2=2，d3=12，d4=12，n=4，q=13，1≤di|q-1，1≤i≤4.

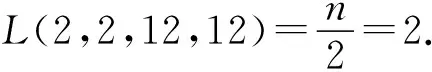
481≤N13(f)≤3913，

(2)

N13(f)≡0(mod13).

(3)

最后，由Maple计算得N13(f)=2041，刚好满足(2)和(3).

4 结 论

通过对一类丢番图方程与有限域上对角方程解的研究，给出了该类丢番图方程的解数当I(d1，…，dn)=11，…，18时，其最小整数解L(d1，…，dn)的值，并推广得到当I(d1，…，dn)=p时，p为素数，L(d1，…，dn)的值.还补充了参考文献[11]中I(d1，…，dn)=6，8，10时，w1，…，wn的具体值，其中wi=gcd(di，lcm[dj:j≠i])，1≤i≤n.

致谢作者非常感谢相关参考文献对本文的启发以及审稿专家提出的宝贵意见.