分数阶非线性薄膜方程的不变子空间和精确解

周碧蓉， 屈改珠

(1.宁波大学 数学与统计学院，浙江 宁波315211； 2.渭南师范学院 数学与统计学院，陕西 渭南714099)

1 引 言

自从1695年在Leibniz和L’Hospital的信件来往中提到非整数阶导数以来，分数阶微积分理论的发展历史已经有三百多年，引起了许多学者的研究兴趣.在二十世纪中后期，分数阶微积分理论的研究更是有了较快的发展.分数阶导数相比较于整数阶导数而言具有全局性，更能帮助从整体上去了解一个函数的一些相关性质.目前分数阶导数的定义方法有许多种[1-2]，其中包括Riemann-Liouville型导数，Caputo型导数以及Grunwald-Letnikov型导数.本文中用到的Caputo导数是在Grunwald-Letnikov型导数的基础上的一种改进，并且当导数的阶数为整数时与Riemann-Liouville型导数的定义是等价的.但含有Caputo导数的方程可以更容易的借助拉普拉斯变换来进行求解.

分数阶偏微分方程有着更为广泛的应用，尤其是在流体动力学等方面，分数阶方程能更清晰的表达其中所蕴含的实际物理意义.对方程精确解的研究也是分数阶偏微分方程发展过程中的热门话题之一.构造整数阶偏微分方程的精确解的方法有很多，比如，首次积分法、李群对称法[3]、Jacobi椭圆函数展开法、试探函数法[4]和不变子空间法[5-6]等.经过学者们的不断研究探讨，发现这些方法也可以同样的应用于分数阶偏微分方程[7-8].

不变子空间法最初是由Galaktionov和Svirshchevski[9]提出并对其进行了进一步的研究发展，而后Gazizov和Kasatkin[10]等人将这一方法推广到了分数阶偏微分方程中，构造求解得到了它们的精确解.不变子空间法是利用偏微分方程的不变子空间构造出方程解的一般形式，将求偏微分方程的精确解问题转化成了求解常微分方程组的问题，大大简化了构造精确解的难题.

文章的第二节和第三节分别回顾了分数阶微积分算子的一些计算性质以及不变子空间方法，第四节则是求解了几类非线性薄膜方程的精确解，最后得到了结论.

2 分数阶微积分计算基本性质

本节将回顾分数阶微积分理论中的一些基本定义性质和运算法则.

定义1[11]函数f(t)的分数阶Riemann-Liouville积分可表示为

其中t>0，α>0，且

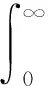
定义2[11]函数f(t)的Caputo型分数阶导数可表示为

其中t>0，α>0，n为正整数.

Caputo型导数相较于其他的定义方法而言更有利于方程的求解.

性质1[11]上述的Caputo型微分算子满足以下的一些性质：

特别地，当0<α<1时，有

3 不变子空间法

在求解整数阶微分方程的精确解时，不变子空间是一个强而有力的计算工具.而在经过Gazizov和Kasatkin等人的研究计算后，不难发现，仍可以相应的使用不变子空间法来构造并解得分数阶微分方程的精确解.

对于方程

定义3[9]若对算子F，一个n维线性组合的子空间Wn满足F(Wn)⊆Wn，则称Wn为F的不变子空间.

假设Wn=L{f1(x)，f2(x)，…，fn(x)}为F[u]的不变子空间，那么方程有形如

u(x,t)=C1(t)f1(t)+C2(t)f2(t)+…+Cn(t)fn(t)⊆Wn

的解.其中Ci(t)为关于t的任意函数.

将解代入原方程则能得到一个n维的常微分方程组

其中Ψi满足：

F[u]=Ψ1(C1，…，Cn)f1+…+Ψn(C1，…，Cn)fn.

求解该常微分方程组后便能得到精确解的具体形式.

性质2[11]对于一个n阶线性常微分方程

L[y]=y(n)+a1y(n-1)+…+any=0，

其中ai为任意常数，并且n≤2k+1.若满足:

u(x,t)=C1(t)f1(t)+C2(t)f2(t)+…+Cn(t)fn(t)，L[F[u]]|L[u]=0=0，

那么Wn=L{f1(x)，f2(x)，…fn(x)}在算子F下保持不变.

4 分数阶薄膜方程的精确解

这一部分将用不变子空间法构造一类分数阶非线性薄膜方程

的一些精确解，其中β1，β2，β3都为常数.

(i)取β3=a1(1-β1-β2)，则方程变为

(1)

由性质2可得该算子F在子空间W2=L{1，e-a1x}下保持不变，即该方程有以下形式的指数型解

u(x,t)=C1+C2e-a1x，

其中C1，C2为关于t的函数，将该形式的解代入方程可得

则相对应的分数阶常微分方程组为

情形1: 当β1+β2=1时，有

(2)

易得C1=const=c，那么有

(3)

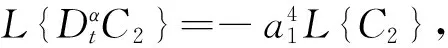
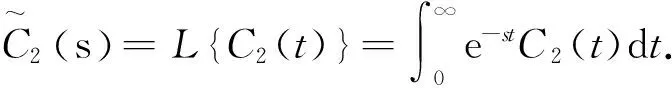
其中Eα，β(z)为Mittag-Leffler函数:

因此，通过求解不变子空间所对应的分数阶常微分方程组(2)得到了该方程的一类精确解

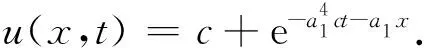
情形2: 当β1+β2=0时，有

(4)

由方程组(4)中的第一个方程可解得

将其代入第二个方程得:C2=t-α，因此，分数阶薄膜方程的精确解为

(ii)取β1=β3=0，β2=1，则方程变为

(5)

可以求得该方程有不变子空间W3=L{1，sinx，cosx}.所以方程有(5)如下形式的解

u(x,t)=C1+C2sinx+C3cosx，

(6)

C1，C2，C3为关于t的函数，将形如(6)的解代入方程(5)可得

F[u]=-C1C2sinx-C1C3cosx.

相应的分数阶常微分方程组为

(7)

不妨设C2(0)=C3(0)=1，则对方程组(7)求解可得

所以方程(5)有精确解

u(x,t)=c+Eα，1(-ctα)sinx+Eα，1(-ctα)cosx.

(iii)取β3=0，那么方程变为

(8)

通过性质2可知该算子F在子空间W5={1，x，x2，x3，x4}下保持不变，即方程具有如下形式的解

u(x,t)=C1+C2x+C3x2+C4x3+C5x4，

C1，C2，C3，C4，C5为关于t的函数，将其代入方程(8)可得

所以在该不变子空间下的分数阶常微分方程组为

首先可解得

则依次可解得

由此可以得知该类分数阶薄膜方程具有精确解

其中

5 结 论

借助不变子空间法，拉普拉斯变换以及Mittag-Leffler函数的一些基本性质，得到了分数阶非线性薄膜方程的指数型、三角函数型和多项式型的解.当然，通过不同类型的子空间，就可以解得不同类型的精确解.这样一来，可以根据实际问题的需求来构造相应的不变子空间，使得不变子空间的应用范围有了大幅度的扩展.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.