向量组的极小生成组

2022-05-07严质彬

大学数学 2022年2期

严质彬

(哈尔滨工业大学(深圳)理学院，广东深圳518055)

1 引言

线性相关、线性无关、秩等概念，是线性代数教学的一个重点.用消元法求解具体的线性方程组，中学生完全理解并能熟练运用.用行列式解线性方程组，虽然推导和总结出公式的过程有些冗长，但是从思想和概念的层面来说，学生也容易理解，无非是用字母表示数来得到一个解的公式.正是线性相关性一系列概念的引入，才使得对线性方程组这个具体数学对象的研究，注入了现代抽象数学的观点，也就是不变量的观点.解线性方程组的消元过程受人为选择的影响，随不同的选择而千变万化，但结果不随这些不同的选择而变化.捕捉变化过程中不变的东西，正是驱动数学发展的一个不竭的动力.利用秩的概念，人们把线性方程组是否有解，以及解集合描述成了方程组本身内蕴的性质.

线性代数教学中，可以借助于几何向量(有向线段)是否共面的几何直观及代数刻画来引入线性相关等概念[1-2].本文引入向量组的生成组和极小生成组的概念，并用它们刻画线性相关和极大线性无关组，为线性相关性理论的教学提供一些参考.关于线性相关性理论的教学，近年来文献中还有一些有趣的研究[3-5].

下文所说的数，都是属于一个指定的数域；所说的向量，都是属于该数域上的一个指定的向量空间.

2 线性相关概念的教学难点

向量组α1，…，αm称为线性相关，如果存在不全为零的m个数k1，…，km，使得

k1α1+…+kmαm=0.

下面指出，正是系数不全为零这个特殊要求，导致了学生在理解和逻辑方面的双重困难.理解方面的困难在于，初学者一时难以琢磨出要求系数不全为零的动机是什么. 一些教材会引导学生观察有向线段共面的几何现象及其代数刻画[1-2]，再引出线性相关的上述定义. 然而，好奇心驱使人们进一步追问，为什么要在向量空间中模仿共面的概念呢？本文后面三节的内容，可以看作是按这个问题驱动，来实施线性相关概念的教学.

至于逻辑方面的困难，则在于系数不全为零这个条件，使得线性相关的逻辑否定，也就是线性无关的刻画有一定的难度. 具体来说就是双重否定以及必要条件等有关的逻辑技巧，初学者一般不能熟练运用. 多年的教学实践表明，在讲解线性相关概念时，作一些逻辑上的铺垫是非常有益的. 要引导学生体会“A仅当B”，或者说必要条件的逻辑含义:A仅当B，也就是自然语言中所说的“只有B，才有A”，指的是从A可以推出B.于是有

向量组α1，…，αm线性无关

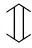
向量组α1，…，αm线性相关的否定

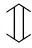
不存在不全为零的m个数k1，…，km，使得k1α1+…+kmαm=0.

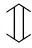
只有全为零的m个数k1，…，km，才使得k1α1+…+kmαm=0.

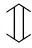
如果k1α1+…+kmαm=0，则m个数k1，…，km必须全为零.

注意上述第三个等价关系还用到下面这个关于双重否定的事实:

不存在不全为零的m个数k1，…，km

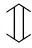
只有全为零的m个数k1，…，km.

3 在线性相关之前引入线性表示

向量β可由向量组α1，…，αm线性表示是指: 存在m个数k1，…，km，使得

β=k1α1+…+kmαm，

(1)

称向量组β1，…，βt可由向量组α1，…，αm线性表示，如果每个βk，1≤k≤t都可由向量组α1，…，αm线性表示.

向量概念引入之后，可以直接讲线性表示[2，6，7]. 由于(1)式中对m个系数没有特殊要求，也就没有上节指出的逻辑上的难点. 从理解上说，学生在中学数学和物理中，已经学习了向量的合成与分解，并用这种观点来理解坐标系. 在此基础上引入线性表示是自然的. 另一方面，利用线性表示的语言，可以立即给出线性方程组有解的一个等价表述: 右端项作为列向量可由系数矩阵的列向量组线性表示. 教材[2，P80]对此给出了有启发意义的评论，“这个结论开辟了直接从线性方程组的系数和常数项判断方程组有没有解的新途径.” 这样学生很快能体会到引入线性表示概念的一种合理的动机了.

线性表示的概念动机明确容易理解，逻辑上又没有上节分析线性相关概念时指出的难点，因此建议在线性相关性理论的教学及线性代数教材的编写中，不要把线性表示概念的陈述，推迟到线性相关之后.

4 向量组的生成组

设{j1，…，jt}是{1，…，m}的一个子集合. 向量组αj1，…，αjt称为向量组α1，…，αm的一个部分组. 注意按集合论规定，一个集合是它自己的一个子集合.

定义1向量组α1，…，αm如果可由它的一个部分组αj1，…，αjt线性表示，则称这个部分组αj1，…，αjt是α1，…，αm的一个生成组.

定理1向量组α1，…，αm线性相关，当且仅当存在α1，…，αm的生成组αj1，…，αjt满足t

证充分性. 令

{jt+1，…，jm}={1，…，m}{j1，…，jt}，

也就是{j1，…，jt}在{1，…，m}中的余集. 由t

αjt+1=k1αj1+…+ktαjt.

它可以写成

k1αj1+…+ktαjt+(-1)αjt+1+0αjt+2+…+0αm=0，

这里k1，…，kt，-1，0，…，0是不全为零的m个数，所以α1，…，αm线性相关.

必要性. 已知有不全为零的m个数k1，…，km，使得

k1α1+…+kmαm=0.

不妨设km≠0. 则有

于是α1，…，αm-1即是α1，…，αm的一个生成组，且m-1

设αj1，…，αjt是α1，…，αm的一个生成组，如果t

推论1向量组线性无关，当且仅当不存在比它小的生成组.

如果一个向量组有比它小的生成组，可以解释说，这个向量组可以利用线性运算，也就是加法和数乘法进行简约. 至于这种简约有什么意义，可以从下面这个容易观察和理解的现象来引导学生体会[3，8]. 从线性方程组中去掉一些多余的方程后，所得到的方程组与原来方程组同解. 对不可简约及可简约进行逻辑刻画，就解释了为什么要引入线性无关及线性相关的概念了.

5 极小生成组

定义2设αj1，…，αjt是向量组α1，…，αm一个部分组. 称αj1，…，αjt是α1，…，αm的一个极小生成组，如果

(i)(生成性)αj1，…，αjt是α1，…，αm的一个生成组；

(ii)(极小性)α1，…，αm没有比αj1，…，αjt更小的生成组，即对{j1，…，jt}的任何真子集{k1，…，ks}，αk1，…，αks不是α1，…，αm的生成组.

定理2设向量组αj1，…，αjt是向量组α1，…，αm的一个部分组. 则αj1，…，αjt是α1，…，αm的一个极小生成组，当且仅当，αj1，…，αjt是α1，…，αm的一个极大线性无关组.

证若t=m，则由定理1可知结论成立. 下面假定t

充分性. 为证明定义2中要求的生成性，任取p∈{1，…，m}{j1，…，jt}. 由极大线性无关组定义，部分组αj1，…，αjt，αp线性相关. 再由αj1，…，αjt本身线性无关，易知αp可由αj1，…，αjt线性表示. 定义2中要求的极小性可由αj1，…，αjt线性无关及定理1可得.

必要性. 由定义2中的极小性知αj1，…，αjt本身也没有更小的生成组. 因此由推论1知αj1，…，αjt线性无关. 任取p∈{1，…，m}{j1，…，jt}. 由定义2中的生成性知αp可由αj1，…，αjt线性表示，从而部分组αj1，…，αjt，αp不是线性无关的. 证毕.

从线性方程组中去掉多余的方程，直到再没有多余的方程可去掉为止，就能自然地引出极小生成组的概念. 极小生成组等价于极大线性无关组，实在是数学之美的又一次展示. 可以顺便开阔一下视野. 假如系数不是取自一个域，而是取自一个环，这种等价不再成立，线性相关性的理论就没有这么简单优美了; “环上的线性方程组”是许多表面上相去甚远的问题共同的数学实质; 在环上研究这类问题，是一些前沿研究领域所关心的，如代数K理论.