升弓和降弓状态下高速列车受电弓非定常气动特性的研究
2022-05-07贾丽荣
贾丽荣, 王 聪, 周 丹
(1.中车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.中车青岛四方车辆研究所有限公司,山东 青岛 266031;3.中南大学 交通运输工程学院,湖南 长沙 410075)
在高速运行状态下,高速气流产生的空气动力对列车运行的影响越来越大,而在影响列车空气动力学性能的众多因素中,大风是一个非常重要的因素[1-2]。其中受电弓由于其整体非流线型外形构造,受到的影响更为剧烈,因此,分析横风下高速列车受电弓的气动性能是非常重要的。由于列车风和环境风的耦合导致受电弓后部产生强烈的气流激扰,使得受电弓的受力有明显的非定常特性,而采用定常方法会把流动中的一些非定常特性过滤掉,往往不能得出受电弓的振动频率等。因此,为保证高速列车性能可靠,必须研究横风下受电弓的非定常气动特性。然而,气流扰动不仅影响升弓状态下受电弓非定常气动特性,还可能对降弓状态的受电弓产生明显影响,比如加剧受电弓振动强度,甚至产生被动升弓现象[3]。由此可见,研究大风作用下升弓和降弓状态下高速列车受电弓非定常气动特性是非常有必要的。
日本和韩国的学者对受电弓气动性能的研究较多。韩国研究人员Lee等人对矩形和流线型的1/4缩比弓头模型进行了风洞试验和数值模拟,对比分析了2种外形下的受电弓气动性能及其构件对总阻力和总升力的贡献[4]。日本学者Ikeda和Suzuki等通过风洞试验和数值模拟对不同截面形状弓头模型进行了一系列的优化[5-6]。
从2006年开始,国内学者对受电弓气动特性的研究增多。风洞试验方面,蔡国华和张永升等采用风洞试验研究了开口和闭口条件下受电弓气动阻力和动态接触压力[7-8]。张冰等研究了气动力作用对弓网受流的影响,得出调整受电弓气动力特性能有效改善弓网受流性能的结论[9]。张雷等采用风洞试验研究了受电弓及其附件的形状对高速列车气动特性的影响[10]。
在数值模拟方面,李田等对比分析了高速受电弓在开口和闭口2种运行状态下的流场特性和气动力特性[11]。郭迪龙等采用受电弓模型,运用分离涡方法分析了受电弓在不同车速、不同风速下气动特性[12]。赵萌等对比分析了受电弓-接触网和受电弓-接触网-列车在不同横风条件下的气动特性,得出车体的存在对受电弓的气动阻力、升力和俯仰力矩产生了显著影响[13]。姚远等人研究了开口和闭口运行条件下的受电弓非定常升、阻力特性,得出运行方式对受电弓及其滑板的升力波动影响明显[14]。牛纪强等采用延迟分离涡模型研究了不同导流装置下受电弓及各构件非定常气动力及波动特性[15]。李晓芳等采用延迟分离涡方法研究了不同侧偏角下受电弓及各构件非定常气动力及波动特性。目前国内外对于受电弓的受力特性研究主要是定常状态时的升、阻力研究,研究对象也是简化的受电弓模型,对降弓状态受电弓的非定常气动特性鲜有涉及。
本文采用延迟分离涡(DDES)方法,以车体-受电弓精细化模型为对象,对大风作用下升弓和降弓状态受电弓周围非定常流场和气动特性进行探讨。
1 数值计算模型
1.1 数值计算方法
文中计算采用DDES方法求解整个流场,DDES方法可视为非稳态RANS(雷诺平均纳维-斯托克斯)方法与LES(大涡模拟)方法的结合。相较于LES方法,DDES方法在整个边界层区域采用非稳态RANS方法求解,其消耗的计算资源较少。用LES方法对其余部分进行模拟,大尺度的分离涡可得到较好地模拟[16-17]。RANS方法中采用SSTκ-ω两方程模型,在该模型中,模型长度尺寸dDDES被用作特征尺寸,计算公式如下:
dDDES=d-fdmax(0,d-CDESΔ)
(1)
fd=1-tanh([8rd]3)
(2)
(3)
式中:d——壁面和第一层网格之间的距离;
Δ——(Δx,Δy,Δz)最大网格;
CDES——该模型中默认常数,取CDES=0.65;
fd——开关函数,fd在LES区域为1, 在边界层区域为0;
rd——当地湍流尺度与距离壁面距离的比值;
νt——运动黏度;
ν——涡流黏度;
ui,j——速度张量;
κ——卡门常数;
y——距离壁面距离。
1.2 计算模型
以列车高度H为特征长度,文中计算模型为头车(6.88H)+中车(6.6H)+尾车(6.88H)的1∶8缩比模型。列车模型包含转向架、风挡以及受电弓的精细结构,受电弓位于中车后部,如图1(a)所示。受电弓主要结构从上到下依次为弓头、上框架、下臂杆、拉杆和基座,如图1(b)所示。

图1 列车及受电弓模型
1.3 计算网格
采用OpenFOAM2.3.1软件中的SnappyHexa程序生成模型网格,网格以六面体为主。网格采用逐层加密的方式进行4层加密,在列车附近网格最密,对受电弓等重点关心部位进行单独加密。在车体及受电弓表面分别设置6层和4层边界层网格,受电弓表面第一层网格厚度为0.097 mm,网格总数为4 468万,计算网格如图2所示。

图2 计算网格
1.4 计算域及边界条件
为保证横风下列车周围流场的充分发展以及减小边界条件的影响,计算域的长度设为70H,列车前部的距离为14H,列车后部的距离为35.35H,列车距离横风入口为10H,距离横风出口为20H,计算域的高度为10H。计算域尺寸及边界条件如图3所示。将面ABFE、面BCGF设为速度入口,面ADHE、面CDHG设为压力出口(相对压强P=0),列车表面给定无滑移壁面边界条件,地面给定滑移壁面边界条件(与列车运行速度相同)。
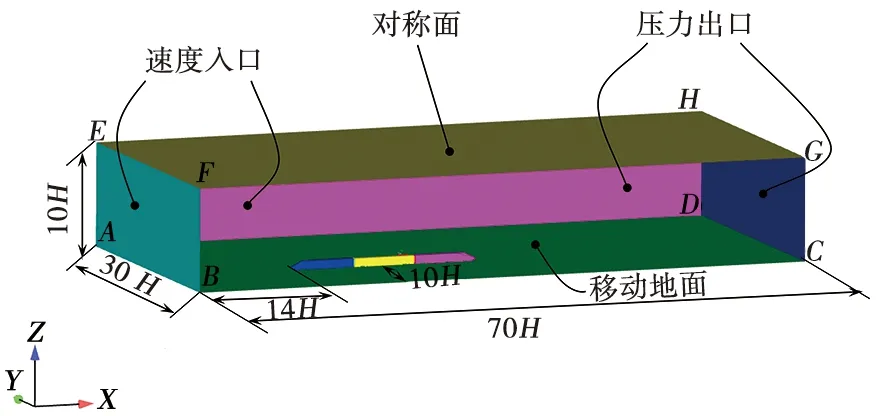
图3 计算域尺寸及边界条件
侧偏角体现了列车速度和环境风速度的耦合关系,其定义为列车反向速度与环境风速度合成后,其合成方向与列车运行反方向呈现的夹角。本文研究了60 m/s气流作用下侧偏角为20°时列车顶部受电弓的气动特性。
基于气流速度60 m/s,马赫数大约为0.18,按不可压缩黏性流考虑;基于气流速度和列车高度,雷诺数为2×106,列车周围的流动为高湍流流动。本次计算中速度压力耦合采用SIMPLEC算法,压力项采用标准格式进行离散,动量项采用中心差分格式进行离散,湍流模型采用二阶迎风格式进行离散;采用双时间步长控制,时间采用二阶隐式格式推进,时间步长为1.0×10-4s,内迭代步数为30,并且30步后可以收敛,流动变量的残差收敛准则设为10-5。
为了消除流场瞬态行为,在流场稳定后开始采样并且平均流场结构。气动力系数采用0.6~2 s平均。
为便于分析,定义各气动力系数如下:
(4)
(5)
(6)
式中:CD——阻力系数;
D——阻力;
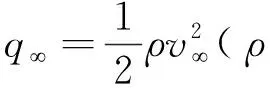
S——参考面积,取1∶8缩比尺度下列车横截面面积,S=0.175 m2;
L——升力;
C——侧力;
CL——升力系数;
CC——侧力系数。
1.5 数值可靠性验证
为验证数值计算的可靠性,将数值计算结果和风洞试验结果进行对比。风洞试验是在中国气动力研究与发展中心的8 m×6 m风洞第二试验段进行的,地板装置是由5块独立地板拼接而成,中间地板有可旋转360°的转盘[18]。为了减少对气流的干扰,地板前后缘加工成流线型。安装完地板后,试验段有效尺寸为16.1 m×8 m×4.9 m(长×宽×高),横截面面积是39.2 m2。风洞试验装置见图4。

图4 风洞试验装置
数值模拟中建立与风洞试验相同的列车-受电弓缩比模型,来流速度设为60 m/s,侧偏角为20°(和风洞试验速度一致),以保证风洞试验与数值模拟的马赫数、雷诺数等相关参数的一致;将地面设为无滑移壁面边界条件,以保证和风洞试验的地面条件一致。所得计算结果与风洞试验对比结果如表1所示,可以看到数值计算结果和风洞试验结果差距不超过10%,满足本文计算要求。

表1 数值计算与风洞试验结果对比
2 计算结果分析
2.1 流场特性
图5显示了由时均速度渲染的升弓和降弓状态下受电弓附近的Q等值面图,Q定义为:
Q=-1/2∂ui,j∂uj,i
(7)
式中:uj,i——速度张量。
Q可以很好地捕捉流场中涡的位置[19]。受电弓在高速运行时,在其后方形成一系列的旋涡结构,这些涡沿着受电弓迎风面的边缘生成,并不断地向后方脱落、破裂。受到列车外流场的影响,受电弓基座和下臂杆底端部分的流场扰动十分紊乱。可以看到降弓状态受电弓高度显著降低,弓头、上框架、下臂杆收于列车顶部,这些部件所引起的旋涡和基座所引起的旋涡融合在一起。
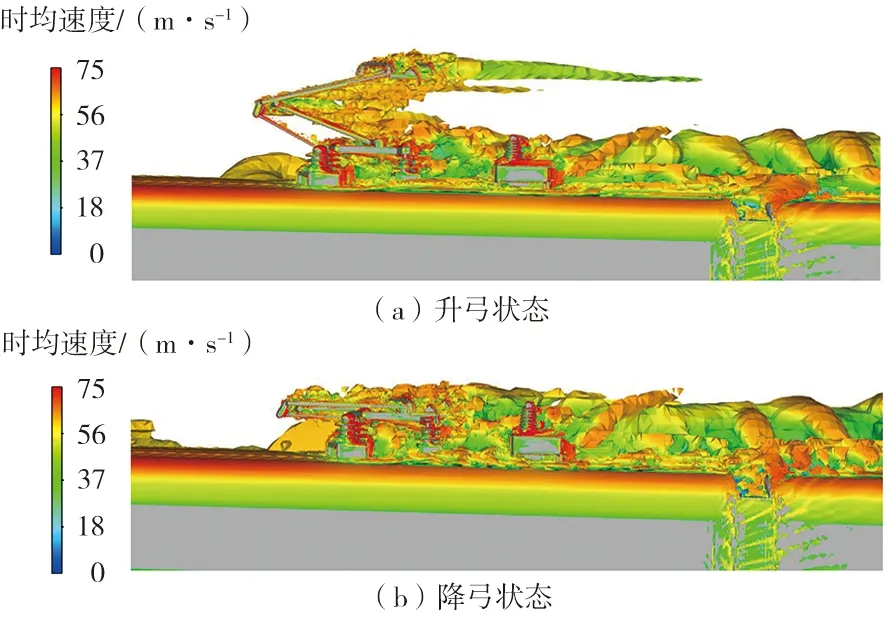
图5 升弓和降弓状态下受电弓附近的Q等值面图(Q=20 000)
针对瞬态流场,用涡量云图显示旋涡的强度。涡量定义为速度场的旋度,强度由下式求出:
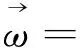
(8)


x、y、z——空间坐标;

u、v、w——速度的分量。
本文中所有涡量云图都取自计算时间t=2 s时刻的流场。
图6为升弓和降弓状态下受电弓纵剖面涡量云图。从图6可以看到,弓头、上框架和下臂杆以及上框架和拉杆连接处、基座后部、列车顶部涡量强度较大。降弓状态由于弓头及杆件收在列车顶部,基座附近的涡量强度比升弓状态更大。

图6 升弓和降弓状态下受电弓纵剖面涡量云图
图7为升弓和降弓状态下受电弓表面时均压力云图。从图7可以看到,升弓状态下弓头、上框架和拉杆连接处以及基座的迎流面出现较大正压,部件的背风面出现较大范围负压;前滑板迎流面受气流的直接作用主要为高压,后滑板迎流面受前滑板和支撑机构尾流的影响高低压交替出现。降弓状态基座表面压力与升弓状态基本相同,弓头及上框架收于列车顶部,受气流直接作用减小,弓头位于基座和上框架所形成的尾涡影响范围内,高压范围减小,下臂杆位于上框架和基座形成的空腔内,受到的压力较小。

图7 升弓和降弓状态下受电弓表面时均压力云图
图8为升弓和降弓状态下受电弓附近的时均速度云图。从图8可以看到,气流在遇到弓头、上框架和拉杆连接处以及基座后受到较大影响,速度变低,部件后部形成低速尾流。2种状态基座部位气流变化不大,升弓状态下臂杆引导气流高速流动;而降弓状态杆件空间角度发生变化,对气流的引导作用减弱,弓头处于基座所引起的尾流范围,气流波动性变大,非定常性较强,受电弓高度较低,对列车顶部流场的干扰范围减小。
2.2 气动力特性
表2、表3分别为受电弓及各部分构件在升弓和降弓状态下阻力系数的时均值及标准差。

图8 升弓和降弓状态下受电弓附近的时均速度云图
从表2、表3中可以看出:降弓状态下弓头阻力系数时均值低于升弓状态,这是因为降弓状态气流对弓头的作用减弱;降弓状态下弓头阻力系数标准差高于升弓状态,这是因为弓头处于基座所引起的尾流范围,气流波动性较大。降弓状态下上框架、下臂杆、拉杆阻力系数时均值和标准差均小于升弓状态,这是因为升弓状态各杆件具有空间角度使其迎流面积更大;降弓状态下各杆件标准差均小于升弓状态,下臂杆最为明显,这是因为降弓状态下下臂杆被包围状态在腔体中。降弓状态下基座阻力系数时均值及标准差和升弓状态相差不多。降弓状态下整弓阻力系数时均值和标准差均小于升弓状态。

表2 受电弓及各部分构件在升弓和降弓状态下阻力系数时均值

表3 受电弓及各部分构件在升弓和降弓状态下阻力系数标准差
表4、表5分别为受电弓及各部分构件在升弓和降弓状态下升力系数的时均值及标准差。从表4、表5中可以看出:降弓状态下弓头、上框架升力方向与升弓状态下相反,其标准差却略小于升弓状态,这是因为2种状态弓头、上框架附近流场受基座的影响,旋涡方式不同。降弓状态下下臂杆升力系数时均值小于升弓状态,升力方向与升弓状态下相反,且接近于0,其标准差也小于升弓状态,这是因为降弓状态下下臂杆处于其他杆件所包围的腔体内,周围流场较为稳定。降弓状态下拉杆升力方向与升弓状态下相反,幅值较大,标准差较小。降弓状态下基座和整弓升力系数时均值及标准差和升弓状态都很接近。
表6、表7分别是受电弓及各部分构件在升弓和降弓状态下侧力系数的时均值及标准差。从表6、表7中可以看出:降弓状态下弓头侧力系数时均值低于升弓状态,其侧力系数标准差和升弓状态下差别不大,这是因为降弓状态下弓头附近流场的非对称性小于升弓状态。降弓状态下上框架的侧力系数时均值高于升弓状态,其侧力系数标准差和升弓状态差别不大。降弓状态下下臂杆侧力系数时均值小于升弓状态,其侧力系数标准差远小于升弓状态,这是因为降弓状态下下臂杆处于其他杆件所包围的腔体内,流场较为稳定。降弓状态下拉杆的侧力系数时均值大于升弓状态,其侧力系数标准差小于升弓状态。降弓状态下基座和整弓侧力系数时均值略小于升弓状态,其侧力系数标准差也小于升弓状态。

表6 受电弓及部分构件在升弓和降弓状态下侧力系数时均值

表7 受电弓及各部分构件在升弓和降弓状态下侧力系数标准差
3 结论
本文采用DDES对升弓和降弓状态下列车-受电弓运行进行模拟,对受电弓Q等值面图,涡量云图、压力云图,时均速度云图以及气动力系数时均值和标准差进行了研究,得到了以下结论:
(1) 升弓和降弓对受电弓弓头及各杆件非定常气动特性的影响较大。降弓状态下受电弓各杆件收缩于列车顶部,杆件对气流的导流作用减弱,受电弓对列车顶部流场的扰动范围减小。
(2) 降弓状态下上框架和下臂杆位于弓头和基座所形成的空腔内,受到的压力减小,气动力系数也大幅度减小;弓头作为受流作用的关键部件,其气动力系数也减小,阻力系数时均值、升力系数时均值、侧力系数时均值分别减小了21.4%、45.5%、28.5%。
