北京地铁DKZ4型车关键系统使用寿命及运用可靠性研究
2022-05-07邬春晖赵媛媛杨建虎霍苗苗汤劲松龚晓波
邬春晖,赵媛媛,杨建虎,白 翔,霍苗苗,阎 锋,汤劲松,龚晓波
(1. 北京市地铁运营有限公司 运营二分公司,北京 100043;2. 北京市地铁运营有限公司 地铁运营技术研发中心,北京 100082;3.中车青岛四方车辆研究所有限公司,山东 青岛 266031)
北京地铁1号线DKZ4型车于1999年投入运营,截至目前已经运用超过20年,最高运营里程已达210万km,即将面临使用寿命保障修工作,而保障修方案需依据车体结构的总寿命制定。另外,该型车于2010年第一次厂修(120万km)过程中,对车辆各关键系统进行了相应改造及更换。因此,有必要开展对DKZ4型车关键系统使用寿命及可靠性评估研究工作,进而为保障修方案的制定提供理论支撑。
1 技术路线制定
轨道车辆是由车体、转向架、牵引系统、制动系统等多个系统和部件组成的复杂机电系统。在工程实践中,无法使车辆所有系统都达到同一寿命周期,因此,所谓“车辆寿命”,实际是由那些价值较高、不可或不易更换且没有自然老化的部件的极限寿命所决定[1-2]。图1为2017年1月—2019年12月期间,北京地铁1号线DKZ4型车各系统故障占比分布图。由图1可知,在此期间造成车辆维护及运营服务故障次数较多的子系统依次为车门系统、牵引辅助供电系统、广播系统、制动系统和机械系统(车体、转向架等),因此,从故障发生的频率及对列车运行安全性的影响程度等方面综合考虑,将车体、转向架、车门系统、牵引辅助供电系统及制动系统(上述系统占总故障比例的72%)确定为DKZ4型车关键系统。

图1 北京地铁1号线DKZ4型车各系统故障占比分布图
综上所述并总结国内外轨道车辆结构使用寿命和可靠性评估技术和经验[3-7],本次将以DKZ4型车车体结构使用寿命评估为核心,同时结合转向架构架使用寿命评估以及车门系统、牵引辅助供电系统和制动系统运用可靠性评估展开相关研究。
2 研究工作开展情况
2.1 使用寿命评估
本次研究采用线路实测应力谱作为输入,并基于工程中较为成熟的名义应力有限疲劳寿命计算方法及累积损伤法则对车体、转向架构架进行疲劳寿命评估。北京地铁1号线DKZ4型车设计寿命为30年,年运营里程约12万km,上述车辆结构的使用寿命主要取决于支撑相应结构的主要梁件,车体主要承载梁件包括牵引梁、枕梁和侧梁等,转向架构架主要承载梁件包括侧梁、横梁等,原则上取这些梁件疲劳寿命的最小值作为相应车辆结构的使用寿命。
动应力测试选取状态检查、无损检测之后的Mc车和T0车作为被试车辆,测试对象包括Mc车和T0车车体以及相应的动车、拖车转向架构架和半永久车钩,被试车辆见图2。应力测点主要布置于无损检测时发现的存在缺陷的关键部位,疲劳强度计算获得的强度薄弱部位,修补或检修过程中确定的危险部位以及其他类似地铁车辆曾经出现故障的部位。另外,为准确模拟列车实际载客运营状态,分别测试了列车在50%AW2、AW2和130%AW2这3种载重状态下的动应力,车辆载重状态见图3,列车运行线路图见图4。动应力测试完成后,结合实际线路情况对实测信号进行去除零漂、奇异值剔除和数字化滤波等处理,并采用雨流计数法对测试获取的应力时域动态信号进行统计,获取不同载重状态下的应力谱。

图2 被试车辆

图3 车辆载重状态

图4 列车运行线路图
针对上述车辆结构,本次评估考虑了两部分的疲劳损伤,即列车运行过程中由于惯性载荷产生的疲劳损伤以及列车到站后上下客产生的疲劳损伤。在列车运行过程中产生的疲劳损伤中,考虑了列车在不同载重状态下运行对车辆结构疲劳寿命的影响,具体评估流程如下文所述。
(1) 根据测点部位结构形式、应力方向、焊接状态等信息,从IIW-2259:2015标准中选取与测点部位相对应的细节类型、FAT等级和Δσ-N曲线[8]。
(2) 根据Palmgren-Miner法则,计算各测点分别在50%AW2、AW2和130%AW2状态下的疲劳损伤Ds。具体计算公式如下:
(1)
(2)
(3)
式中:ni——第i级应力范围的循环次数;
Ni——第i级应力范围相对应的疲劳寿命;
Δσi——第i级应力范围;
ΔσR,L——拐点处应力范围特征值;
C1、C2——Δσ-N曲线方程中的常数;
m1、m2——Δσ-N曲线方程中的指数。
(3) 根据1号线列车实际运营情况,统计50%AW2、AW2和130%AW2这3种载重状态的运行比例,并基于50%AW2、AW2和130%AW2测试应力谱产生的疲劳损伤,计算列车到达设计寿命时,列车运行过程中产生的疲劳损伤Dd。具体计算公式如下:
(4)
式中:L——车辆目标运营里程;
Li——不同载重状态下的应力谱测试里程;
αi——车辆不同载重状态的平均运行比例;
Dsi——不同载重状态测试应力谱对应的疲劳损伤。
由于列车实际运营过程中,其载客量是连续变化的,因此,需根据1号线列车的实际运营情况,将连续变化的载重量等效到50%AW2、AW2和130%AW2这3种典型载重状态下,并确定它们的运行比例[9]。根据1号线分时断面客流量统计表和运营时刻表,可知30 min内(如8:00—8:30)各运行区间(如军事博物馆站至木樨地站)运送的乘客数量以及30 min内各运行区间经过的列车数量,由此,可以估算出每列车顺序行经各个区间的列车载客量,从而进一步换算出列车载重量。图5为列车在典型工作日和周末从投入运营到退出运营期间,顺序经过各个区间的载重状态变化情况。
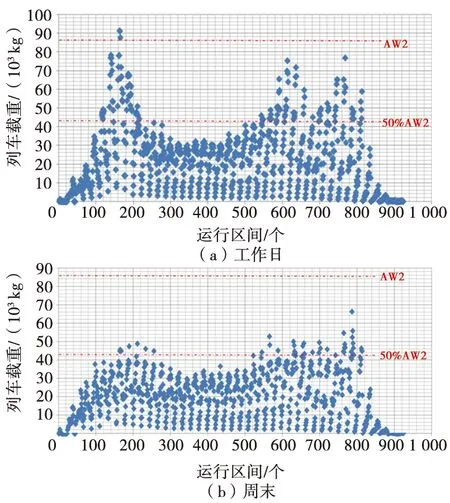
图5 典型工作日和周末列车载重量动态变化
为确定50%AW2、AW2和130%AW2这3种典型载重状态的运行比例,保守考虑,采用以下等效假定:载重量≤50%AW2时,用50%AW2状态等效;50%AW2<载重量≤AW2时,用AW2状态等效;AW2<载重量≤130%AW2时,用130%AW2状态等效。由此,根据上述获取的列车1天时间的载重量数据,经过等效可以计算出列车不同载重状态的平均运行比例以及每年不同载重状态的运行里程,不同载重状态的平均运行比例及年运行里程见表1。
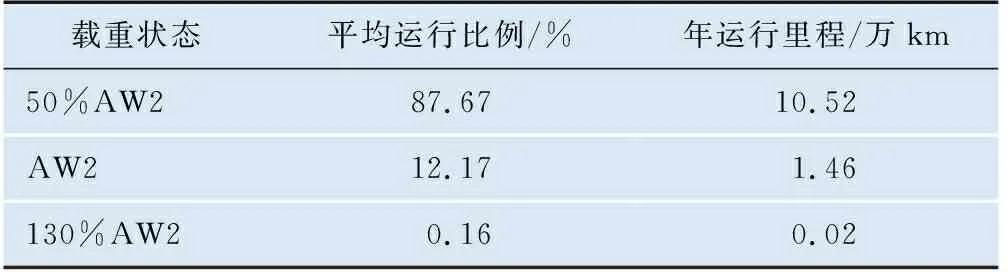
表1 列车不同载重状态运行信息
(4)为了模拟列车实际运营情况,计算列车到达设计寿命时,因列车到站后上下客产生的疲劳损伤。基于1号线的运营情况,本次研究做出如下假定:列车始发站初始状态为空车(AW0),列车运行过程中最大载重为AW2,到达终点站后清客(AW0),形成一次载荷循环(AW0-AW2-AW0);另外,列车全程23站,其中换乘站8站,非换乘站13站,换乘站乘客变化量为30%AW2(AW2-70%AW2-AW2),非换乘站乘客变化量为20%AW2(AW2-80%AW2 -AW2)。因列车到站后上下客产生的疲劳损伤Dp的计算公式如下:
(5)
式中:L0——单个往返里程;
n2——单个往返经过的换乘站数量;
n3——单个往返经过的非换乘站数量;
NT1——车辆载重变化相对应的各测点疲劳寿命;
NT2——换乘站车辆载重变化相对应的各测点疲劳寿命;
NT3——非换乘站车辆载重变化相对应的各测点疲劳寿命。
(5) 计算列车到达设计寿命时,车辆总疲劳损伤D。计算公式如下:
D=Dd+Dp
(6)
(6)计算车辆安全运用里程Ls。计算公式如下:
(7)
由车辆结构疲劳寿命评估结果可知,车体结构疲劳损伤较大部位主要分布在牵引梁与下盖板焊缝处、牵引梁腹板与车钩座焊缝处、枕内纵向梁焊缝处和侧梁与枕梁焊缝处,疲劳损伤较大部位统计结果见表2和表3。在车体结构主要承载梁件区域,Mc车2位端牵引梁与下盖板焊缝处、T0车1位端牵引梁与下盖板焊缝处疲劳损伤值均大于1,最大疲劳损伤值为1.173,换算后可得安全运用里程为255.8万km,无法满足设计寿命要求;其余测点区域均有较高的疲劳强度裕量,安全运用里程均大于360万km。

表2 Mc车车体疲劳损伤较大部位统计结果

表3 T0车车体疲劳损伤较大部位统计结果
转向架构架疲劳损伤较大部位主要分布在一系簧座与侧梁下盖板焊缝处、电机座上盖板与横梁焊缝处、小纵梁与横梁焊缝处,疲劳损伤较大部位统计结果见表4和表5。在动车转向架构架主要承载梁件区域,电机座上盖板与横梁焊缝处、牵引座上盖板与横梁焊缝处疲劳损伤值均大于1,最大疲劳损伤值为1.751,换算后安全运用里程为171.3万km,无法满足设计寿命要求;其余测点区域均有较高的疲劳强度裕量,安全运用里程均大于360万km。拖车转向架构架主要承载梁件区域均有较高的疲劳强度裕量,安全运用里程均大于360万km。

表4 动车转向架构架疲劳损伤较大部位统计结果

表5 拖车转向架构架疲劳损伤较大部位统计结果
2.2 运用可靠性评估
本次研究基于DKZ4型车2017年—2019年维护及运营服务故障数据,首先对车门系统、牵引辅助供电系统和制动系统近3年的维护及运营服务故障率进行计算;之后采用统计模型方法确定上述关键系统的运营服务故障分布模型,进而预测其平均故障间隔时间(MTBF)、可靠寿命等可靠性指标;最后通过对上述关键系统进行FMECA分析(故障模式、影响及危害度分析),评估每一部件故障模式对系统的影响及危害性[10-11]。关键系统可靠性分析流程见图6,FMECA分析流程见图7。

图6 关键系统可靠性分析流程
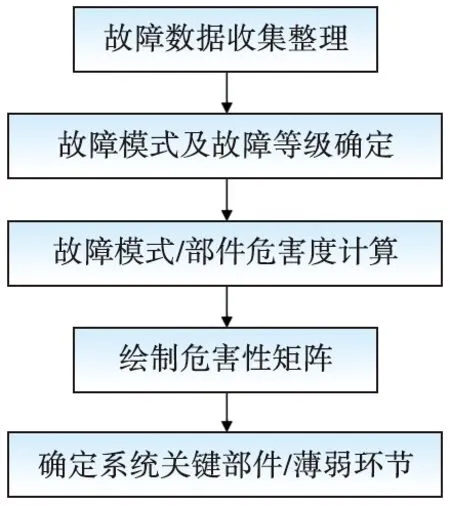
图7 FMECA分析流程
故障数据统计依据以下原则进行:(1)由人为因素造成的系统故障,在计算可靠性时不计入;(2)系统偶然出现故障、重启后能恢复正常工作的,同一种偶然故障在24 h内累计达3次计1次处理,不足3次时不计入;(3)故障修复后累计工作不足24 h,再次发生同一故障的,只记录1次。
故障率λ为各系统工作到某一时刻尚未故障,在该时刻后单位时间内发生故障的条件概率,在工程实际中,可以用某一时间段内发生故障的频率作为近似值,即:
(8)
式中:N——各系统规定时间内的故障总次数;
t——各系统规定时间内的累计工作时间。
可靠性工程中常用的分布模型主要有指数分布、威布尔分布及对数正态分布等。对于一组未知分布类型的故障数据,可首先假设该组故障数据符合所有的备选分布模型,然后对每一种模型进行拟合,最后选取拟合优度最好的分布模型,进行参数估计和假设检验,并验证所选模型的正确性。
FMECA是分析系统中每一部件所有可能的故障模式及其对系统可能造成的所有影响,并按各故障模式的严重程度及其发生概率确定其危害性的一种系统可靠性分析方法。通过FMECA分析可全面识别影响系统可靠性的关键部件、缺陷及薄弱环节,部件危害度Ci计算公式如下[12]:
(9)
式中:Cij——部件i的第j个故障模式的危害度;
αij——部件i以故障模式j发生故障的频数比;
βij——部件i发生故障模式j时的故障影响概率;
λi——部件i的故障率;
t——部件i规定时间内的累计工作时间。
车门系统、牵引辅助供电系统和制动系统近3年的维护及运营服务故障率统计结果分别见表6和表7。由表6和表7可知,车门系统维护故障率已超出相应故障率指标,但呈逐年下降趋势;运营服务故障率呈波动状态,2019年故障率高于相应故障率指标;牵引辅助供电系统维护故障率低于相应故障率指标,运营服务故障率呈逐年增加趋势,2019年运营服务故障率高于相应故障率指标;制动系统维护故障率低于相应故障率指标,运营服务故障率高于相应故障率指标。

表6 关键系统维护故障率统计结果 次/万km

表7 关键系统运营服务故障率统计结果 次/万km
根据3种关键系统运营服务故障间隔时间数据做线性拟合,采用决定系数和均方根误差进行拟合优度检验,各分布的拟合相关性参数见表8。由表8可知,针对3种关键系统,相较于威布尔分布和对数正态分布,指数分布的决定系数更加接近1,均方根误差更小。进一步采用K-S检验法对所选分布模型进行假设检验,取显著性水平α=0.05,结果见表9。由表9可知,K-S检验值Dn<临界值Dn,α,h=0,原假设成立。因此,3种关键系统运营服务故障间隔时间均服从指数分布。

表8 关键系统运营服务故障间隔时间拟合相关性参数
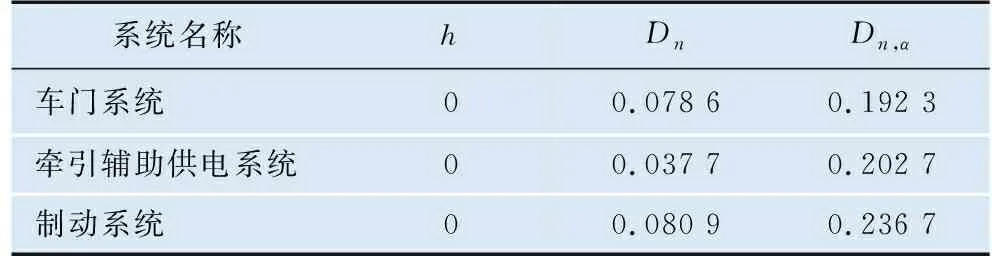
表9 K-S检验结果
3种关键系统运营服务可靠性评估结果表明,车门系统、牵引辅助供电系统和制动系统的平均故障间隔时间均低于相应评价指标(8 976 h、11 041 h和44 336 h),对于31组列车总体而言,车门系统平均约每24天发生一次故障,牵引辅助供电系统平均约每27天发生一次故障,制动系统平均约每67天发生一次故障。关键系统可靠性函数及可靠性指标见表10。

表10 关键系统可靠性函数及可靠性指标
关键系统FMECA分析结果表明,车门系统在维护故障及运营服务故障情况下危害度最高的部件均为门风缸,危害度分别为143和12,危害性矩阵见图8。牵引辅助供电系统在维护故障情况下受流器的危害度最高,在运营服务故障情况下辅助逆变器(SIV)的危害度最高,危害度分别为25和20,危害性矩阵见图9。制动系统在维护故障情况下防滑传感器的危害度最高,危害度为4,在运营服务故障情况下继电器和空气开关的危害度最高,危害度均为3,危害性矩阵见图10。
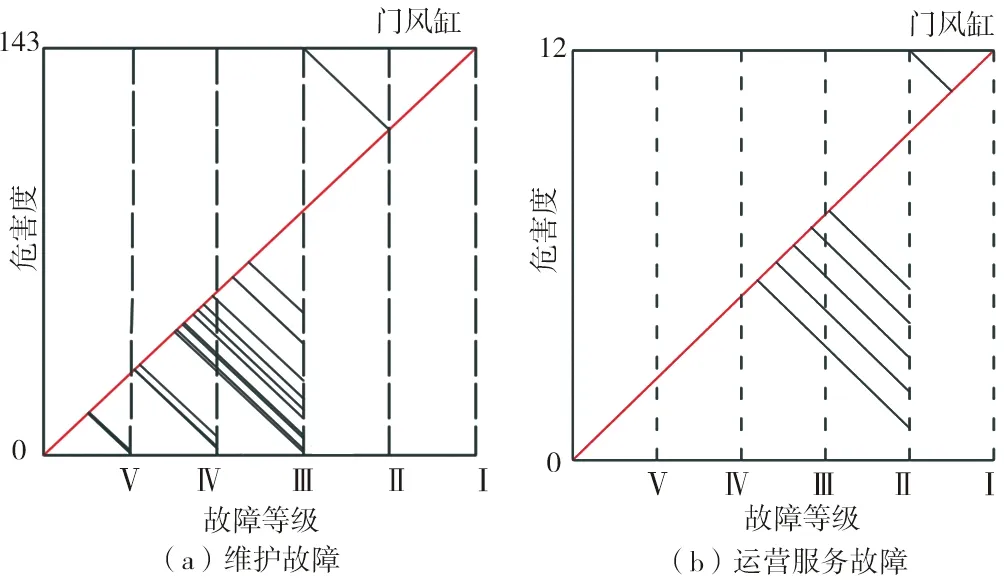
图8 车门系统危害性矩阵

图9 牵引辅助供电系统危害性矩阵

图10 制动系统危害性矩阵
3 结论与建议
通过开展北京地铁1号线DKZ4型车关键系统使用寿命及运用可靠性研究,可得出以下结论及建议:
(1) 在车体结构主要承载梁件区域,Mc车二位端和T0车一位端牵引梁与下盖板焊缝处疲劳损伤值均大于1,最大安全运用里程为255.8万km;建议在运用中对所有DKZ4型车车体上述疲劳薄弱部位进行监控,并在保障修中对相关部位进行状态普查和无损检测,进行相应补强处理。
(2) 在转向架构架主要承载梁件区域,动车转向架构架电机座上盖板与横梁焊缝处、牵引座上盖板与横梁焊缝处疲劳损伤值均大于1,最大安全运用里程为171.3万km;建议在运用中对所有DKZ4型车动车转向架构架上述疲劳薄弱部位进行监控,并在保障修中对相关部位进行状态普查和无损检测,必要情况下进行局部结构补强或者补焊处理。
(3) 车门系统的维护故障率高于相应评价指标;车门系统、牵引辅助供电系统和制动系统的运营服务故障率和平均故障间隔时间均无法满足相应评价指标,3种关键系统分别平均约每24、27和67天会发生一次故障;建议据此合理安排检修周期,并加强维保和安全监控。
(4) 在维护故障及运营服务故障情况下,车门系统、牵引辅助供电系统和制动系统中危害度最高的部件分别为门风缸,受流器和SIV,防滑传感器、继电器和空气开关;建议在日常维修中应重点关注上述关键故障部件,必要情况下,可在保障修中对其进行更新处理。
