聚焦高考真题 提升创新思维
2022-05-07福建徐祖德
福建 徐祖德
创新是一个民族的灵魂,创新能力是社会经济文化发展的重要助推力,也是学生在青少年阶段集中体现的特征性能力.高考数学试题对创新能力考查主要体现在对创新思维的要求,增强试题的开放性.一方面,要求学生能够打破常规思路,主动思考,积极探索;另一方面,要求学生能够将多种思维融合,创造性地解决问题.
创新思维的基础是逻辑思维,不同于一般思维的常规性、单向性和单一性,它体现的是思维的创见性、发散性和综合性.创新思维是一种求异的思维活动,以求异而非求同为其价值导向,它要求无论是在思考问题的方式、方法上,还是在思维活动的结果方面,都要与传统的思维活动有着不同的新颖之处.
高考试题承载着引导教学的功能,作为重要的教学素材,试题的价值一直被教师在教学中深入思考、充分挖掘,高考真题对引领、把握教学导向起着重要作用.在教学中如何用好高考真题进行有效的教学设计和组织,提升学生创新思维,结合笔者的教学实践谈谈几点想法.
一、关注情境,激发主动
余文森教授认为“情境之于知识,犹如汤之于盐,盐要溶于汤中才能被吸收,知识也要融入情境之中,才能显示活力和美感,才能被学生理解、消化、吸收”.思维主体的主动性是创新思维的重要驱动因素,在教学中,当学生完成某项活动时,教师应创设适当的情境,激发学生的主动性,唤醒其创新意识,驱动其自身的行动,鼓励其付出努力和实践,引导其逐渐形成良好的创造能力.


本案例利用优秀传统文化的民间剪纸艺术情境,有机渗透数学建模、数据分析、逻辑推理等数学核心素养与数学思想方法的应用,鼓励学生在主动探索中,体验从特殊到一般的探索数学问题的过程,形式新颖,取材真实情境,解决实际问题,感受数学的应用价值.
二、尊重独创,鼓励求异
在新思想、新观点和新方法的发现上,创新思维明显表现出独创性特征,因其建立在独立思考的基础之上,并表现出其中的差异性.因此教学中要鼓励学生不受已经形成的思维定式和思维惯性的禁锢,打破思维界限,创设让学生有机会对相关知识的理解和应用提出自己的见解的条件,引导学生站在已有知识系统的基础之上,尊重学生提出合理的新的突破点,欣赏学生找到的解决问题的新思路,激发学生从多角度认识问题,深化理解水平,展示其创新思维的求异性.
【案例2】(2021·新高考Ⅰ卷· 7)若过点(a,b)可以作曲线y=ex的两条切线,则
( )
A.eb B.ea C.0 D.0 常规解法: 在曲线y=ex上任取一点P(t,et),对函数y=ex求导得y′=ex,所以y=ex在点P处的切线方程为y-et=et(x-t),即y=etx+(1-t)et, 由题意可知,点(a,b)在直线y=etx+(1-t)et上,可得b=aet+(1-t)et=(a+1-t)et, 令f(t)=(a+1-t)et,则f′(t)=(a-t)et, 当t 当t>a时,f′(t)<0,此时函数f(t)在(a,+∞)上单调递减, 所以f(t)max=f(a)=ea, 由题意可知,直线y=b与曲线y=f(t)的图象有两个交点,则b 当t 当0 创新解法: 画出函数y=ex的图象如图所示,根据直观图即可判定点(a,b)在曲线下方和x轴上方时才可以作出两条切线,由此可知0 题目设置情境是学生熟悉的,针对本案例,教师可以让学生直接运用导数的几何意义先求出切线方程,再利用点在切线上转化为直线与曲线有两个交点问题,这有利于学生掌握通性通法.然而,教师能否在教学中抓住问题的本质,帮助学生寻求简化的解决思路呢?可以的!本案例的创新解法就是通过发现并利用图象的特征,大幅度减少了运算量,达到快速求解的目的.在教学中应该鼓励学生寻求创新,对一道题目研究的越充分,学生从中受到的启发就越多,创新思维就越强,学习印象就越深刻. 发散性是指在创新思维的形成过程中将思维客体的相关要素进行联系.教师可以在教学设计中指导学生进行发散性思维训练,让学生扩展思考和讨论某一问题的条件和结论,并结合相关知识,举一反三,深入研究其本质,从而理解问题.发散性思维可分为横向发散思维和纵向发散思维.横向发散思维主要包含了对一个问题的理解,带动相似问题的理解和解决,并找出其中的共性,得出其本质规律.纵向发散思维是指将一个简单的问题进行深化,在条件进一步深入的情况下,提出新的设想,分析新出现的问题,并思考其解决办法,也就是要大胆怀疑,精心求证.总之,发散性思维就是将一个问题进行灵活多样的发散思考,从不同的角度来思考同一个问题,将其融会贯通. (1)求C的方程; (2)0 试题解析: 本题主要考查双曲线的定义及其几何性质、直线与双曲线的位置关系、韦达定理等内容,能力层面突出考查学生的推理论证能力、运算求解能力以及综合运用所学知识分析问题和解决问题的能力,侧重考查逻辑推理、数学运算和数学抽象等数学核心素养.试题分两问,梯度明显,第(1)问比较简单,注意自变量的范围即可;第(2)问,可以先将直线方程与曲线方程联立,再结合韦达定理表示弦长,进而利用|TA|·|TB|=|TP|·|TQ|转化为两直线斜率的关系,求得结果. 反思第(2)问的解题过程及结果来看,若点T所在直线换成x=m上,直线AB的斜率与直线PQ的斜率之和又如何?若将双曲线一般化,直线AB的斜率与直线PQ的斜率之和又会是多少?若将双曲线改为椭圆或抛物线,结论是否有变化? 通过以上的发散性思维思考与训练,可以得到如下统一结论:对于任意圆锥曲线,曲线上四点共圆的充要条件是其中两点连线的斜率与另外两点连线的斜率之和为零. 关注综合性是指要在教学中注重引导学生能够正确处理整体和个体的关系.学生不仅要解决个体问题,更要从整体上思考问题的来龙去脉,即要能够挖掘表现形式不同但实质相同的问题,在解决一个问题的同时能解决一系列问题.教师在教学中要正确处理模式化和创新之间的关系,结合学生实际的认知水平,从各种信息中提炼出有用的条件,将其归纳、整理,进行深层的挖掘和分析,并总结反思分析和解决问题的思维过程,使学科的重点知识、技能方法成为学生分析、解答问题的有效工具,从而达到提升学生创新思维发展的目的. 【案例4】(2021·新高考Ⅰ卷·22)已知函数f(x)=x(1-lnx). (1)讨论f(x)的单调性; 试题解析: 导数教学中有这样的一种套路:先求导,再解方程找零点,确定单调区间比较大小,实在不行二次求导.这样机械记忆的方法,虽然有对系列问题的思考,但是忽略了问题本质,只是在教导学生片面形式记步骤. 在本案例中,如果还利用这样的求导方法,学生是很难完成作为压轴题的函数与导数问题的.这时候就要学会整体思考.王雅琪老师曾指出,学生对导数问题的解答一般要经历四个环节:分析问题、构建函数、研究函数、解决问题.学生面对问题,首先是弄明白要干什么,要解决的问题是什么,或更高一点,它能转化成什么问题;接下来是思考为了解决上面的问题,有可能用到的函数是什么,学生要根据问题构建恰当的函数意识和基本方法.导数的考查不只停留在利用导数研究函数性质的层面,要能够利用刚构建的函数性质去解决问题.认清这类问题的本质,再回头看上面的第(2)问,就明白了如何通过构建函数解决问题了. 第(2)问的解法: 因为f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)max=f(1)=1,且f(e)=0, 不妨令x1∈(0,1),x2∈(1,e),则2-x1>1, 先证2 即证x2>2-x1, 即证f(x2)=f(x1) 则h′(x)=f′(x)+f′(2-x)=-lnx-ln(2-x)=-ln[x(2-x)]>0, 所以h(x) 因此2 同理,要证x1+x2 即证f(x2)=f(x1) 则φ′(x)=-ln[x(e-x)],令φ′(x0)=0, x∈(0,x0),φ′(x)>0,x∈(x0,1),φ′(x)<0, 又x>0,f(x)>0,且f(e)=0,故x→0,φ(0)>0,φ(1)=f(1)-f(e-1)>0, 所以φ(x)>0恒成立,x1+x2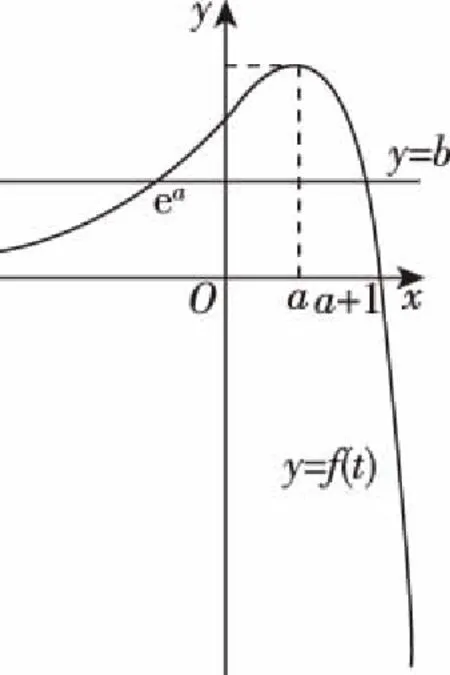

三、拓展思维,注重发散



四、关注综合,注重整体