习题课教学中的拓展与延伸

甘肃 陈鸿斌

习题课是教学中必不可少的一部分,它不但能起到对已学知识的复习,而且能将所学知识进行应用,并掌握一些常用的技巧.很多教师在习题课教学中,忽略和遗弃课本,从一些教辅材料中搜集大量的高考题来充满整个课堂.其实这样充其量只做了几道题,重术而不在道,并且大多高考题的起步都很高,对大多数学生不利.高考题源于课本而高于课本,从课本出发,对大多数学生来说是更容易适应,再逐步拓展与延伸,真正做到让学生“跳一跳,够得着”.不仅能让大部分学生跟得上,还能分层次教学.笔者在习题课教学中很注重这一点,在课堂上和同学们一起探究、推广与延伸课本例题、习题,在很大程度上激发学生大胆的想象、创造、发现,经历数学的整个探究过程.这样的习题课教学对学生数学思维的培养有很大的促进的作用,并且还能得到一些漂亮结果.

1.横向多元拓展与延伸

【例1】已知a,b,c都是正数,求证:(a+b)(b+c)(c+a)≥8abc.

本题难度不大,用均值不等式能很快证明此题.

证明: ∵a,b,c>0,

此时,笔者并未就题论题而马上离开此问题,而是引导学生继续探究此题,学生通过观察发现不等式左边的式子中,a,b,c顺次作和走了一个轮回,右边有a,b,c的积,并且由上面的证明知,8可表示为23.从中我们能获得什么信息呢,此问题能否推广呢?

此时,学生A做出如下猜想:

若a,b,c,d都是正数,则(a+b)(b+c)(c+d)(d+a)≥16abcd.

学生按照上面的思路很快证明其是正确的.笔者在此赞扬了同学A,话刚落定,学生B站起来说“若a1,a2…,an都是正数,则(a1+a2)(a2+a3)…(an-1+an)(an+a1)≥2na1a2…an.”

此时,班里大多数学生都非常认同,学生们的热情很高,我格外的称赞了学生B,同学们按照上述证明就毫不费力的证明出此结论.

定理1若a1,a2,…,an(n∈N*,n>1)都是正数,则(a1+a2)(a2+a3)…(an-1+an)(an+a1)≥2na1a2…an.

【例2】已知x,y都是正数,求证:(x+y)(x2+y2)(x3+y3)≥8x3y3.

学生按照例1的证法很容易地解决此题.

笔者在此引导，此题能否与上题一样推广呢？学生C站起来做出下面的猜想:

若x,y都是正数,则(x+y)(x2+y2)…(xn+yn)≥2nxnyn.

那这个猜想对不对呢？这时有的学生表示认同,有的学生开始嘀咕起来.

故而验证学生C的猜想不成立,我也鼓励学生C的表现非凡.

【例3】已知a,b,c是不全相等的正数,求证:a(b2+c2)+b(c2+a2)+c(a2+b2)>6abc.

学生利用重要不等式不难解得本题.

证明:∵b2+c2≥2bc,a>0,

∴a(b2+c2)≥2abc.

同理b(c2+a2)≥2abc,c(a2+b2)≥2abc.

∵a,b,c不全相等,

∴a(b2+c2)≥2abc,b(c2+a2)≥2abc,c(a2+b2)≥2abc三式不能全取等号，故a(b2+c2)+b(c2+a2)+c(a2+b2)>6abc.

笔者继续引导,如果条件中只是a,b,c都是正数,那结论是怎样的呢?

同学们异口同声的说a(b2+c2)+b(c2+a2)+c(a2+b2)≥6abc.

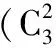
学生D自告奋勇,能将其推广啊!他的猜想如下:

若a,b,c,d都是正数,则

ab(c2+d2)+ac(b2+d2)+ad(b2+c2)+bc(a2+d2)+bd(a2+c2)+cd(a2+b2)≥12abcd.

定理3若a1,a2,…,an(n∈N*,n>2)都是正数,则

2.纵向高次拓展与延伸

【例4】已知a,b是不相等的两个正数,求证:(a+b)(a3+b3)>(a2+b2)2.

利用作差比较,并将其展开不难证明.

证明:(a+b)(a3+b3)-(a2+b2)2

=ab3+ba3-2a2b2

=(ab3-a2b2)-(a2b2-ba3)

=ab2(b-a)-ba2(b-a)

=ab(b-a)2.

∵a,b>0且a≠b,

∴ab(b-a)2>0,

(a+b)(a3+b3)>(a2+b2)2.

笔者引导,请同学们来观察此题,可以知道当且仅当a=b时取等号,不等式左边与右边又有什么关系呢?学生E发现,它们的次数1，2，3是三个连续正整数.

好的!那“若a,b>0,则(a2+b2)(a4+b4)≥(a3+b3)2”是否成立呢?

同学们用作差法很容易证明是正确的.学生F做出猜想:

若a,b>0,则(an-1+bn-1)(an+1bn+1)≥(an+bn)2(n∈N*,n>1).

很多学生似乎都赞同其观点,请同学们来验证其是否成立,学生仍然用作差法证明了此结论.

命题1若a,b>0,则(an-1+bn-1)(an+1+bn+1)≥(an+bn)2(n∈N*,n>1).

笔者继续引导,难道它们的次数就一定是连续的正整数吗?

一个反应快的学生G马上意会我的意思,站起来说:“我猜想,它们的次数是成等差数列的正整数就行了.”

说得非常好!那如何表述呢?

学生G说:“若a,b>0,则(an-d+bn-d)·(an+d+bn+d)≥(an+bn)2(n,d∈N*,n>d).”

下面同学们可以互相讨论、交流来完成证明.

(an-d+bn-d)(an+d+bn+d)-(an+bn)2

=an-dbn+d+bn-dan+d-2anbn

=an-dbn(bd-ad)-anbn-d(bd-ad)

=an-dbn-d(bd-ad)2.

∵a,b>0,n,d∈N*,n>d,

∴an-dbn-d(bd-ad)2≥0.

故(an-1+bn-1)(an+1+bn+1)≥(an+bn)2.

命题2若a,b>0,则(an-d+bn-d)(an+d+bn+d)≥(an+bn)2(n,d∈N*,n>d).

笔者接着引导,它们的次数既然成等差数列,同学们是否还记得它的一个性质呢?若下标之和相等,则对应的项之和相等.

学生们同声:“记得!”

那用到此题中结论还成立吗?

学生开始犯嘀咕了.

好的,我们来一起看一下,是否有下面的结论成立呢?

若a,b>0,m,p,q,n∈N*，m

探索:(am+bm)(an+bn)-(ap+bp)(aq+bq)=ambn+bman-apbq-bpaq=ambq(bn-q-ap-m)-bmaq(bp-m-an-q)

∵m

∴p-m=n-q,

∴ambq(bn-q-ap-m)-bmaq(bp-m-an-q)

=(ambq-bmaq)(bp-m-ap-m)

=ambm(bq-m-aq-m)(bp-m-ap-m)

=ambm(bp-m-ap-m)2(bq-p+abq-p-1+…+baq-p-1+aq-p).

∵a,b>0,m,p,q,n∈N*,m

∴p-m≥1，q-p≥0.

∴ambm(bp-m-ap-m)2(bq-p+abq-p-1+…+baq-p-1+aq-p)≥0.

故(am+bm)(an+bn)≥(ap+bp)(aq+bq).

定理4若a,b>0,m,p,q,n∈N*,m

(am+bm)(an+bn)≥(ap+bp)(aq+bq).