折流坎对竖井旋流式消能工涡室水力特性影响的数值模拟研究

赵国安，杨红宣，沈春颖，徐一民，苟 超，李镇旭

(昆明理工大学 电力工程学院，云南 昆明 650500)

0 引 言

合理高效的消能工布置一直是地势复杂地区水利枢纽建设的难点.竖井旋流式泄洪洞不仅能够适应复杂地形下的消能要求，还能在一定程度上降低工程投资，所以成为了中小型水利枢纽建设的首选[1].旋流消能工通过在洞内布置起旋结构，使水流在特定的部位产生较高的环向流速，同时在水流中心部位形成空腔，通过出口处竖向、水平向水流之间以及水流与空气之间的混掺，以达到消减水能的消能结构，但该形式的消能工对涡室及竖井段的水流流态要求较高，若不对原有体型进行优化，水流通过涡室所形成的流态很难满足工程要求.

曹民雄等[2]较早在国内对涡流式内消能工进行研究，掀起竖井旋流式消能工的研究热潮；牛争鸣等[3]对竖井水平旋流式内消能工的空化特性进行深入探索，对易产生空化的位置及原因进行了分析讨论，并提出减免空化空蚀的措施；Granata[4]通过直接跌落式竖井的物理模型试验发现，直接跌落式竖井虽然结构简单、过流能力大，但是由于消能作用差，水流直接冲击竖井底板，对底板造成较大的冲击破坏，易引起竖井的强烈振动；郭新蕾等[5]采用 VOF 自由液面捕捉方法和 RNGk-ε湍流方程，通过反演不同入流角度下旋流竖井的水力学特性，得出旋流竖井入流角与竖井涡室起旋条件之间的关系；安瑞东等[6]针对深层隧道排水系统对不同结构竖井(旋流式竖井和螺旋阶梯式竖井)水力学特性和调蓄隧道中的间歇喷涌问题进行研究，发现在不考虑竖井直径的条件下，螺旋阶梯式竖井运行风险明显低于旋流式竖井，水力学特性更利于过流消能和与调蓄隧道的水流衔接；南军虎等[7-9]对公伯峡水利枢纽泄洪洞进口和退水洞内宏观的水流流态、旋流洞壁面压强以及泄洪洞消能率进行分析发现，原型观测、模型试验和数值模拟三种方法均能较好地呈现出水流的基本现象和规律，但数值模拟对竖井和退水洞内的水气两相流流态以及边界急剧变化区域压强的模拟效果较弱，在工程设计中需对其进行修正；徐剑乔[10]对涡流式竖井与折板式竖井进行研究指出，涡流式竖井对隧道冲洗强度较小、入流稳定、占地较小，且不需要单独气室，排气效果好，综合认为涡流式竖井略优于折板式竖井.值得指出的是乐丰[11]针对竖井旋流式消力井涡室结构进行了比较系统的改进试验，从加大上游进口段末端的尺寸、在涡室内部设置挑坎等一系列措施对涡室水流进行了分析，得出在进口末端与涡室内部同时设置挑坎对涡室水流的效果最好，并针对涡室内部挑坎体型进行了研究.本文针对折流坎角度以及流量变化对涡室水力特性进行分析，通过建立旋流-竖井式泄洪洞模型，探究其水力特性及其物理本质，为今后的导流洞改建利用问题打下良好的理论基础.

1 试验模型

1.1 物理模型试验设计

试验模型由上游进口段、椭圆弧段、涡室、收缩段、竖井段、消力井、出口段组成，试验模型示意图与连接体形示意图如图1所示.其中，进口段断面采用宽度为 18 cm、底板坡度为5%的泄槽与涡室相连接，进口段长度为 230 cm，进口段与涡室采用1/4椭圆曲线与单圆弧涡室偏心相切连接的形式，折流坎的起始位置距竖井段中心横向距离为 40 cm，涡室直径为 20 cm，涡室高 50 cm，竖井段直径 15 cm，高度为 194 cm(不包含上下渐变段)；消力井直径为 20 cm，井深 35 cm.在涡室与竖井以及消力井与竖井之间设有收缩段，收缩段长度为 20 cm；最后下游采用坡度为2%的泄槽连接.涡室与引水道连接体型分别采用无折流坎(0°)的体型和有折流坎的体型进行对比.通过改变折流坎的倾角，进行多组试验，研究旋流竖井的流态、脉动压力等水力特性，模型材料均采用 8 mm 厚的有机玻璃制成[12].

涡室的测点从边墙椭圆弧段开始布置，沿流程共布置6列(其中第六列的6、11、15、19号测点位于正前方，与第五列呈平面垂直关系)，前五列每列间隔 12.0 cm，纵向布置4排，以底板及其延长线为基准，各排相互平行依次向上移动 3 cm，具体布置情况如图2所示.

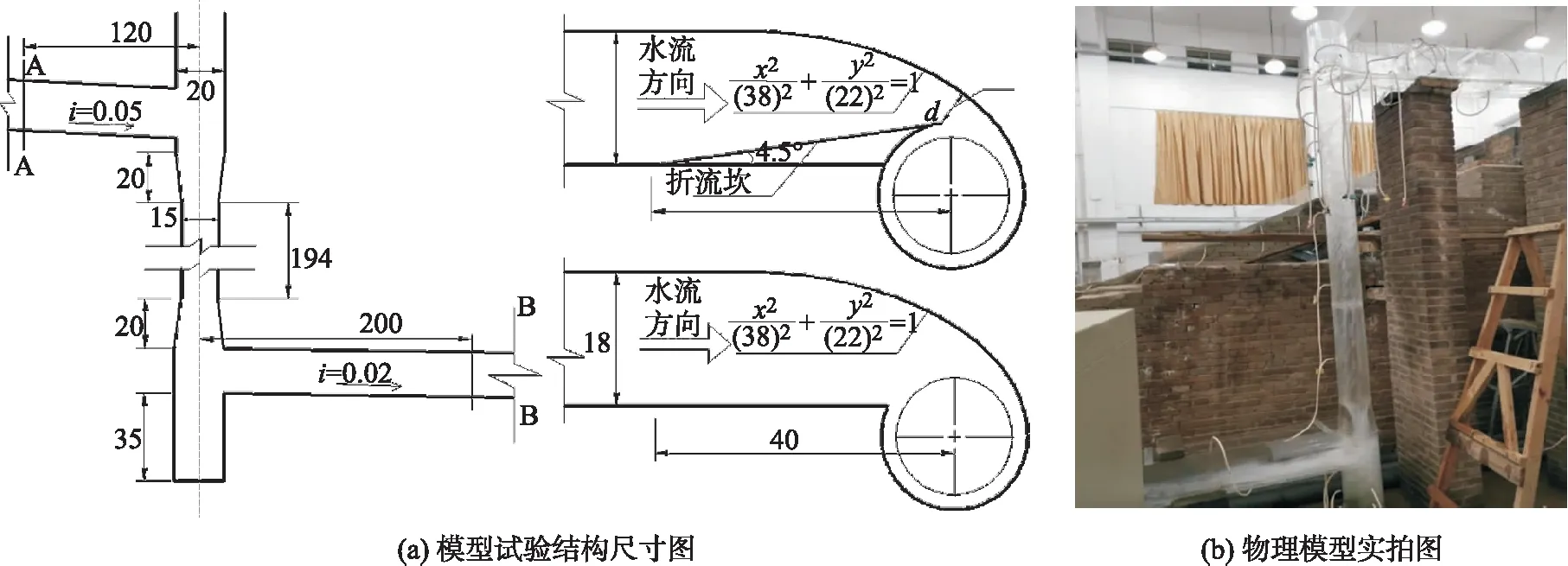
图1 模型试验布置示意图Fig.1 Schematic diagram of model test layout

图2 涡室测点布置图Fig.2 Arrangement of measuring points of vortex chamber

1.2 数值模型设计

相比于标准k-ε湍流模型，RNGk-ε湍流模型通过修正湍动黏度，考虑平均流动中的旋转及旋流流动情况，能够更好地处理高应变率、流线弯曲程度较大的流动，这对分析涡室段的水力特性尤为重要，并且相较于DES、LES模型，RNGk-ε湍流模型采用的是时均值的概念，这和我们的实验值能够较好的吻合，并且所占用的计算资源较少.郭新蕾等[5]通过计算环形堰竖井泄洪洞水流运动情况，对该模型进行了验证，认为该模型计算结果较为准确.本文采用RNGk-ε湍流模型，并结合有限差分法进行数值离散，应用GMIRES迭代法求解代数方程，VOF法进行自由表面追踪.RNGk-ε湍流模型的连续性方程、动量方程及k、ε方程如下：

连续方程：

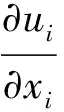
(1)

动量方程：

(2)

k-ε方程 ：

(3)

(4)

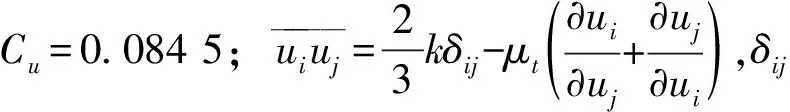
采用Solidworks软件构建数值模型，上游的模拟区域选择在进水口喇叭段末端，下游模拟区域选择在下游泄槽2 m处，进口断面采用速度与流量的边界条件进行控制，出口采用压力出口，整体模型采用结构化六面体网格进行划分.为了能够有效控制进口断面的水利条件，在模型进口处单独划分一个网格单元作为进口断面，以便准确精细地控制入口流量，并且在涡室以及竖井部分进行了局部加密处理.整个模型网格中最大网格尺寸为 0.015 m,最小为 0.005 m，模拟区域的网格总数为148万.

2 试验工况选择与引涡比

2.1 工况选择

为了探究该体型下最佳的适用流量，本文对该体型进行了预放水试验，试验流态表明涡室前连接段及涡室内水流流态与流量及折流坎角度密切相关.无论是流量还是折流坎倾角的增加均会使涡室流态与竖井中的旋转效果更好.为了使旋流-竖井式消能工运行状态更加灵活，并且尽可能不影响其泄流能力，在原有的泄槽段增设折流坎，试验初步选定的折流坎体型为θ=(0°、3°、4.5°、6°)四种体型，过流流量经过无量纲化处理(Q2/gD5,其中D为竖井直径，本文采用 15 cm，处理后的无量纲数称为泄流数)后，泄流数采用 0.006 7、0.010 7、0.016 1、0.018 8、0.021 5 五级流量进行研究.

2.2 引涡比

由于涡室水流流态受折流坎倾角、起始位置以及涡室尺寸等各种因素的影响，为了更好地描述折流坎对涡室水流的影响，引入了引涡比的概念.引涡比是引水道与涡室直接连接部分的最小宽度与涡室直径的比值.通过引涡比的大小可以直观地描述涡室水流的影响，进而确定最佳的引水道与涡室的连接体型.引涡比概念如图3所示.

图3 引涡比概念图Fig.3 Concept diagram of vortex ratio

3 结果分析

3.1 流速分析

为了验证数值计算的准确性，本文对涡室平行于底板的第一排测点(1、2、3、4、5、6)的流速沿程变化情况进行分析，结果如图4所示.

由图4(a)可知，涡室测点的实测流速值普遍低于模拟值，其中最大误差在19%左右，实测值与模拟值的沿程变化趋势一致，具有指导意义.图4(b)表明水流在刚进入到涡室时，由于折流坎以及椭圆边墙的束缚，流速沿程快速降低；在完全进入到涡室后，受重力的影响，水流流速快速增加，而水体受到的重力影响是一致的；在引涡比为0.547时，水体流速的增加速率最大，也意味着其所拥有的环向速度大于其他引涡比的水体，这对竖井段的水流流态有着重要作用.

3.2 流态分析

3.2.1 涡室流态分析

各泄流数下水体在流经引水道与涡室连接的椭圆弧段时，水体受折流坎的影响在康达效应进入涡室后能够紧贴壁面旋转，产生流态稳定的贴壁旋流进入到竖井当中，伴随着泄流数由小逐渐增大以及引涡比的变化，涡室内流态主要呈现出以下几种变化：

当引涡比为0.698，泄流数较小时，涡室进口前椭圆弧段基本无水体壅高现象，对整个消能工的过流能力无影响，但存在小股射流直接射入涡室边壁的现象，使得涡室中的旋流效果不充分，水体直接以自由落体的形式直接砸向消力井的水垫上；随着泄流数的增加，涡室进口前的水体壅高现象会逐渐变得明显，直接射入涡室边壁的小股射流逐渐与受惯性作用的主流汇合，水流从而呈现出跌-旋混合的状态，涡室中的旋流效果依旧没有明显改善.

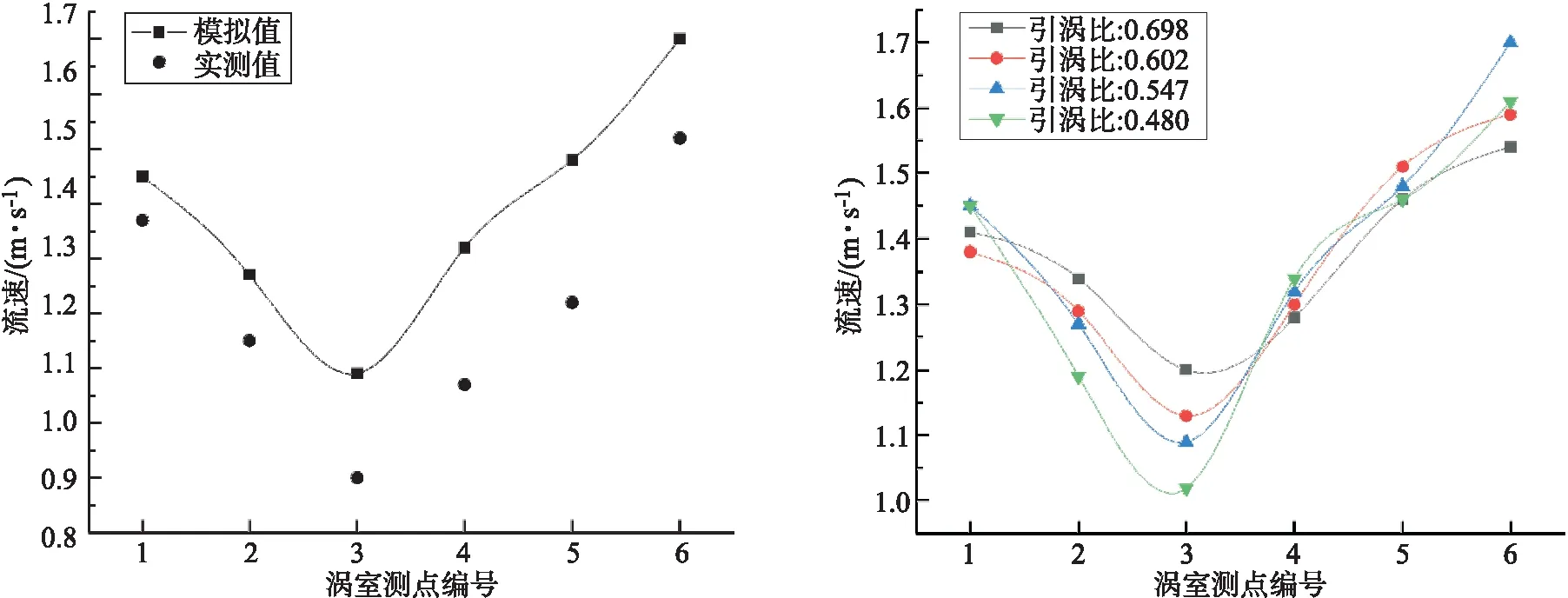
(a)引涡比0.547、泄流数0.0161流速对比图 (b)不同引涡比涡室测点流速分布图图4 涡室测点流速分布图 Fig.4 Velocity distribution of measured points in the vortex chamber

引涡比减小到0.602时，涡室进口前水位壅高会更加明显，射流情形有所改善但主流在涡室中旋转能力依旧不足，随着泄流数的增加，涡室中的小股射流状况会逐渐消失，此时的流态最好，水流几乎全部处于自由旋流的状态.

当引涡比进一步减小到0.48，即使在泄流数很小时，原本存在的小股射流也基本全部汇入主流螺旋下落.但是由于引涡比过小，在泄流数稍有增加时，涡室进口前的水体壅高呈指数形式增长，严重影响整个构筑物的过流能力.各典型工况下涡室流态见图5.

(a)引涡比0.698 泄流数0.016 1 (b)引涡比0.547 泄流数0.011 (c)引涡比0.48 泄流数0.016 1图5 各典型工况下涡室流态对比图Fig. 5 Comparison of vortex chamber flow patterns under typical working conditions

3.2.2 竖井流态分析

由于涡室流态的良好与否直接关系到竖井段水流的水平切向速度进而影响竖井内部的水流流态，若竖井内的水流并未产生良好的水平切向速度，会导致水体经过涡室后在竖井段停留时间较短，直接砸向消力井水垫，使消力井水流流态极其紊乱，轻则导致整个体型达不到设计消能率，需进行二次消能，重则导致下泄水流对下游建筑物造成冲刷破坏，影响建筑物的正常使用.本文针对各工况下的竖井段水流进行了流态分析，重点分析水流在竖井段的流动轨迹，选择各自工况下的单条流线，以此判断竖井内部的水流情况，详细见图6(图像经过变形处理).

由竖井段水流单挑流线轨迹可知，流线会随着引涡比的减小以及泄流数的增大在竖井段内停留较长，但是随着引涡比减小到一定程度时，流线延长的速率逐渐趋于平缓，并且过小的泄流数会导致涡室水体壅高，严重影响过流能力.就竖井内部的水流流态分析而言，引涡比为0.547时较好，对流量的适应能力也较强.

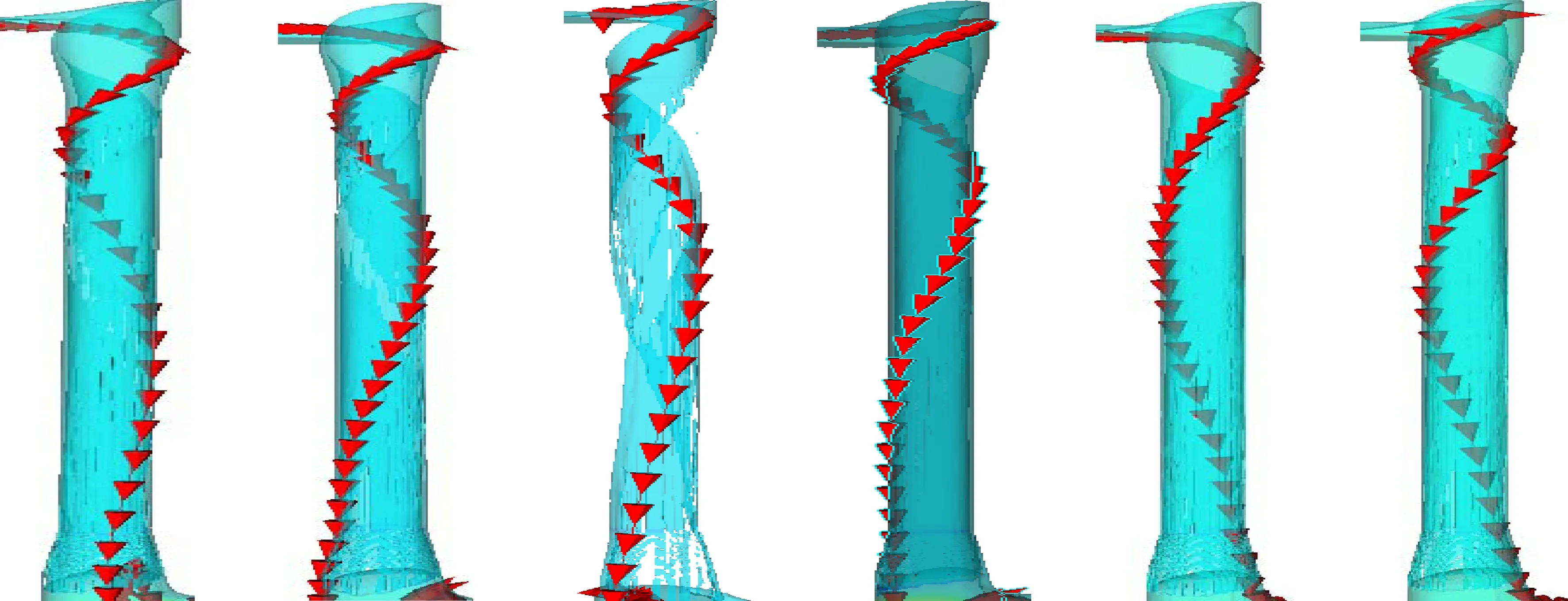
(a)引涡比0.698泄流数0.016 1 (b)引涡比0.602泄流数0.016 1 (c)引涡比0.547泄流数0.006 7 (d)引涡比0.547泄流数0.016 1 (e)引涡比0.547泄流数0.021 5 (f)引涡比0.48 泄流数0.016 1图6 各典型工况下竖井段水流单条流线图Fig.6 Single flow chart of vertical shaft water flow under each typical working condition

3.3 时均压强分析

为了探究不同引涡比下的涡室内部水流的压强特性，本文对涡室内部的水体壁面处的时均压强进行了分析，结果如图7所示.

图7 涡室测点压强分布图Fig.7 Pressure distribution of measured points in the vortex chamber

由图7(a)可知，沿引水道底坡及其延长线上的实测压强与模拟压强值沿程分布基本一致，最大误差在20%以内，并且在折流板末端处壁面的时均压强达到峰值，无论是相同泄流数数值下的不同引涡比，还是相同引涡比下的不同泄流数数值的壁面压强时均值沿程分布规律基本一致.但值得注意的是,当图7(c)以及图7(d)中泄流数数值过高时，无论是沿引水道底坡方向还是垂向，壁面压强时均值均会发生一个明显的偏折，这是由于涡室内部的水流在进行环向运动时，一部分边缘水流受重力作用发生翻滚与主流水体发生掺混所导致，但几乎不会改变主流部分水体的稳定性，可以忽略.

3.4 消能率分析

本次试验消能率的计算选取图1中进口段A-A断面及出口末端B-B断面，各工况总消能率计算值如表1所示.消能率计算公式如下：

(5)

(6)

式中：Z为A-A断面距B-B断面的高差，V1为A-A断面水流平均流速，h1为A-A断面平均水深，V2为B-B断面水流平均流速，h2为B-B断面平均水深，hw为水头损失，η为消能率，g为重力加速度.

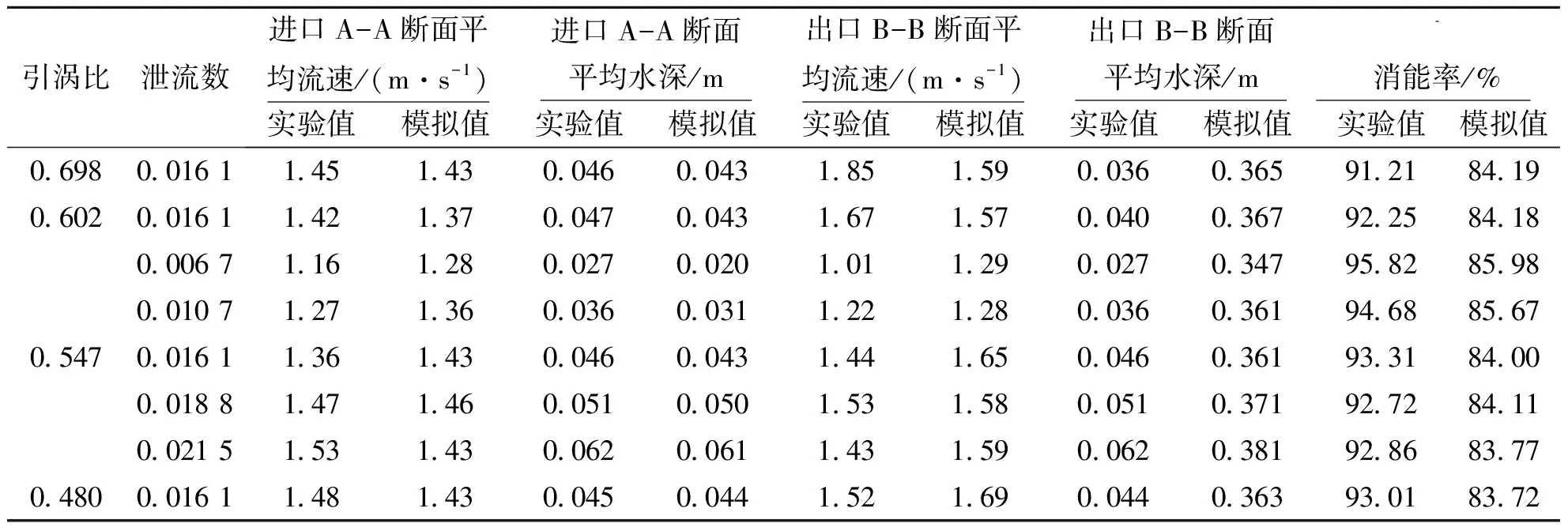
表1 不同工况下的消能率

从表1中各工况下消能率可以看出，实验结果的旋流竖井溢洪道的消能效果总体都能达到90%以上，而数值计算的结果普遍偏低，但也都在83%以上，消能效果明显优于传统形式的消能工，实验值偏高可能是由于实验时尾水的湍动太过剧烈，导致所测得的水深以及流速数值不太准确.通过引涡比与泄流数的改变，发现引涡比在0.547时，整个竖井旋流式溢洪道消能率最高.值得注意的是，无论是哪种引涡比，整个结构的消能效果均随着泄流数的增加呈现出先减小后增大的趋势，这意味着竖井旋流式的消能结构对流量的适应能力极强，值得在今后的工程实际中加以推广.

4 结 论

本文通过改变引涡比以及泄流数数值的大小对涡室内部的水流流态进行了研究分析，得出以下结论：

1)采用RNGk-ε湍流模型可以较好的对涡室内部的水流进行数值分析，其结果经物理模型实验验证可靠度较高；

2)引涡比数值的变化并不会改变涡室内部水流流速、压强等分布规律，只能影响其数值大小；

3)引涡比与流量的增加均会使从涡室进入竖井段的水流环向扰流速度增加，进而使得竖井段的水流下泄流程增加，减小对下游处的影响；

4)在相同流量下引涡比数值的增大会导致整个竖井旋流式消能工的消能效果提高；而在相同引涡比时，流量的增加会导致整体消能效果的下降，但下降效果并不明显，不会对工程产生严重影响.

综合来看引涡比在0.547时，无论是涡室还是竖井段的水流流态都是最优的，既能够使流经涡室处的水流产生较稳定的环向绕流速度，又不会使得引水道与涡室连接处产生较为严重的壅水影响泄流，同时其综合消能效果也达到最优，并且在该体型下泄流数的改变并不会对其消能效果产生较为严重的影响，在实际工程中可以予以考虑使用.