基于门控循环单元神经网络的燃料电池系统故障监测

全 睿，乐有生，李 涛，常雨芳，谭保华

(1. 湖北工业大学 电气与电子工程学院，湖北 武汉 430068；2.湖北工业大学 理学院，湖北 武汉430068)

0 引 言

质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell，PEMFC)是一种将化学能直接转换为电能的发电装置，是一种具有较好发展前景的清洁能源利用方式.质子交换膜燃料电池具有能量转换效率高、零排放或低排放、工作温度低、功率密度大、启动快速等特点[1-2]，在新能源汽车、轨道交通、固定电源等领域具有较好应用价值.质子交换膜燃料电池系统具有一定的复杂性，在运行中可能出现故障，严重情况下可能出现燃料电池堆损坏失效.对燃料电池进行故障监测，有利于获取系统运行信息，提高系统可靠性.

文献[1-4]从模型、数据驱动、实验测试等方面综述了PEMFC系统故障诊断方法，为相关研究提供了重要参考.Yang等[5]采用线性参数可变(Linear Parameter-Varying，LPV)模型描述PEMFC系统行为，提出增强状态观测器(Augmented State Observer)估计系统内部状态和组件故障.Khan等[6]提出了浓差压降的半经验模型，通过计算PEMFC的水含量诊断水淹和膜干故障，并使用蝴蝶优化算法(Butterfly Optimization Algorithm)优化模型参数.文献[7-9]基于电化学阻抗谱提取故障诊断特征，对故障特征进行分类从而诊断PEMFC系统故障.基于解析模型的方法需要建立PEMFC系统的过程模型，克服系统内部参数获取困难等问题.刘嘉蔚等[10]采用线性判别分析和概率神经网络对PEMFC系统的运行数据进行水管理故障诊断，以较高的准确率实现正常状态、水淹故障和膜干故障的诊断.文献[11]基于极限学习机和Dempster-Shafer证据理论对PEMFC系统进行四种不同程度的空气化学计量比故障诊断.Zhang等[12]提出基于模拟退火遗传模糊C-均值聚类(Simulated Annealing Genetic Algorithm Fuzzy C-Means Clustering，SAGAFCM)和深度信念网络(Deep Belief Network，DBN)的故障诊断方法，对去离子水进口高温故障、氢气泄漏故障、空气低压故障和正常状态进行诊断.数据驱动的方法要求收集PEMFC系统的运行数据，针对不同的故障数据训练分类模型进行诊断.在实际中可能难以大量获取故障运行数据.故障数据不足可能导致实际诊断效率不高.

在实际实验中，PEMFC系统的故障运行数据获取成本高，部分故障运行试验可能造成燃料电池堆的性能退化甚至不可逆损毁.相比较而言，燃料电池系统的正常运行数据更容易获取.神经网络具有强大的拟合能力，门控循环神经网络是一种适合序列信息处理的神经网络.使用大量正常运行状态数据可以对燃料电池运行状态进行模拟，对建模困难的复杂系统具有便利性.基于大量PEMFC系统的正常运行数据，本文采用门控循环单元神经网络对PEMFC系统输入输出模型进行模拟，通过预测PEMFC的输出电压进行运行状态监测，诊断系统有无故障.

1 质子交换膜燃料电池系统结构

本课题组研发的40 kW燃料电池系统部分结构示意图如图1所示,主要包括电堆模组、氢气供给子系统、空气供给子系统、水热管理子系统等[13].氢气供给子系统为燃料电池堆供应燃料氢气，同时将未完全反应的氢气分离水分重新送入电堆反应.空气供给子系统提供反应所需的氧气，同时对气体增湿，保持电堆内水分.水热管理子系统采用水作为冷却液，主要是吸收电堆内电化学反应产生的热量和移除多余的水分，维持电堆温度.电堆模组由多片质子交换膜燃料电池单体电池串并联组成，经过DC/DC变换器变换以达到系统输出要求的电压等级.整个系统由各个传感器采集检测信号并送到燃料电池系统控制器进行监测与控制.

2 基于门控循环单元神经网络的监测方法

2.1 质子交换膜燃料电池系统故障监测方案

基于模型的故障监测方法(Model-Based Fault Monitoring Method)通过对实际系统输出物理量与模型预测输出物理量的残差进行分析、处理和决策，判断系统的运行有无故障[1-4].该方法根据实际系统输入变量、中间状态变量、系统输出变量建立系统过程预测模型，将实际系统输出和系统过程预测模型的输出比较产生残差，对残差进行处理决策得到故障信息.

神经网络具有强大的拟合能力，可以用来建立燃料电池的输入输出预测模型.基于历史运行数据，神经网络能够学习和拟合复杂系统的非线性映射和多变量间的关系[1,2,4].通过采集质子交换膜燃料电池系统的运行数据，运用神经网络拟合系统运行过程中的输入变量、中间状态变量、系统输出变量间的映射关系，无需分析系统的机理模型，可以从数据中寻找燃料电池系统的输入输出模型.

图1 燃料电池系统部分结构示意图Fig.1 Schematic diagram of part of the fuel cell system

本文采用的基于门控循环单元神经网络的质子交换膜燃料电池系统故障监测方案如图2所示.通过采集质子交换膜燃料电池系统的运行数据，采用门控循环单元神经网络拟合燃料电池系统的运行行为，得到质子交换膜燃料电池系统输入输出关系模型.该方法将质子交换膜燃料电池系统看作一个黑盒，基于历史运行数据训练门控循环单元神经网络模型，模拟质子交换膜燃料系统[1-2]运行状态.在故障监测时，门控循环单元神经网络模型根据系统当前输入数据，预测燃料电池的输出电压，通过燃料电池的实际输出电压与门控循环单元神经网络模型的预测输出电压的电压残差判断系统运行状态有无故障.

图2 基于门控循环单元神经网络模型的故障监测方案Fig.2 Fault monitoring scheme based on the gated recurrent unit neural network model

电压残差阈值的设置对故障监测具有重要影响.残差处理主要对电压残差进行统计分析，从而为电压残差阈值设置提供参考.本文设置电压残差阈值为三倍测试数据电压残差标准差.假设电压残差为R，测试数据的电压残差标准差为σ，电压残差阈值为Rth，设置电压残差阈值Rth=3σ，当|R|>Rth时判定质子交换膜燃料电池系统处于故障运行状态，否则判断为正常运行状态.

2.2 门控循环单元神经网络结构

门控循环单元神经网络是一种采用门控机制的循环神经网络[14-15].该网络由门控循环单元网络层堆叠而成.门控循环单元网络层的结构如图3所示.

图3 门控循环单元网络层结构示意图(GRU Cell：门控循环单元神经元)Fig.3 Schematic diagram of the gated recurrent unit neural network layer

在门控循环单元神经网络中，网络层由多个基础的门控循环单元神经元组成.同层的门控循环单元神经元采用前后互连的方式提取输入时间序列的信息,其网络权值参数共享以减小参数量、降低参数规模、提高训练效率.门控循环单元神经元包含复位门和更新门两个控制门[13-14].假设x=[x1,x2,…,xN]表示网络层的输入,xt∈Rd(t=1,2,…,N)表示网络层在第t时刻的输入，d表示输入数据的维度，h=[h1,h2,…,hN]表示网络层的输出，ht∈RD表示网络在第t时刻的输出，D表示输出数据的维度，grt表示第t时刻的复位门(下标r表示英文复位reset，区别于更新门,下标t表示第t时刻)，gut表示第t时刻的更新门(下标u表示英文更新update，区别于复位门，下标t表示第t时刻).复位门grt控制接受上一个门控循环单元神经元的输出ht-1的程度.c=[c1,c2,…,cN]表示网络层的新输入，ct∈RD表示网络层在第t时刻的新输入.更新门gut控制当前门控循环单元神经元的输出.门控循环单元神经元的计算如公式(1)～(4)所示[14-15]:

grt=σ(Wrhht-1+Wrxxt+br)

(1)

ct=tanh(grt⊗(Whhht-1+bhr)+Whxxt+bhx)

(2)

gut=σ(Wuhht-1+Wuxxt+bu)

(3)

ht=(1-gut)⊗ht-1+gut⊗ct

(4)

式中：⊗表示两个同维向量或矩阵对应元素相乘运算.t=1,2,3，…,N,N为门控循环单元网络层的神经元个数，h0=0，1表示与gut同维的全一向量.σ表示Sigmoid激活函数，表达式如(5)所示，tanh激活函数的表达式如(6)所示.Wrh、Wrx、br是复位门的参数矩阵或向量，Whh、bhr、Whx、bhx是新输入的参数矩阵或向量，Wuh、Wux、bu是更新门的参数矩阵或向量，这些参数都是可学习的.

(5)

(6)

2.3 门控循环单元神经网络的训练

神经网络的训练过程是优化目标函数的过程.在预测任务中一般采用均方差损失函数.本文采用均方差损失函数.假设门控循环单元神经网络的预测值为f(x;θ)，θ表示神经网络的参数集，预测的真实值为y，均方差损失函数L计算方法为：

(7)

(8)

式中，arg min表示求解使目标函数值最小的参数.

梯度下降算法[16]是神经网络训练的主要算法.在均方差损失函数的最小化优化中使用网络参数θ的梯度迭代更新：

(9)

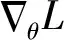
针对大规模数据，我们通常使用小批量梯度下降法[17].设每次选取B个样本组成集合Sk，第k次迭代时梯度计算公式为：

(10)

图4 算法流程图Fig.4 Algorithm flowchart

基于门控循环单元神经网络的算法流程图如图4所示.首先通过实验收集燃料电池的正常运行数据，对收集到的数据进行数据预处理；然后将预处理后的数据集随机分为训练集和测试集，用训练集训练网络，用测试集对网络进行测试评估.若神经网络满足要求，则完成网络训练工作，否则重新收集数据扩大数据集，或者重新配置网络超参数，或者重新训练网络，直到达到要求.

2.4 数据预处理及燃料电池系统数据集

(11)

图5显示了归一化后的部分状态变量变化情况.

图5 某段时间部分状态变量变化情况(数据已归一化，纵轴为无量纲量)Fig.5 Some state variables in a certain period(Variables in the vertical axis have been normalized and are dimensionless)

将标准化后的数据处理成门控循环单元神经网络的数据格式，得到燃料电池系统数据集，如表1所示.数据集共有 42 997 个样本，每个样本由(x，y)组成，其中x代表神经网络的输入，y代表相应的电堆1#电压和电堆2#电压的真实值.

按照8∶2的比例将数据集随机划分为训练集和测试集，即训练集共有 34 397 个样本，测试集共有 8 600 个样本.训练集数据用于训练网络，测试集数据用于对完成训练的网络进行测试评估.

图6 门控循环单元神经网络配置Fig.6 Gated recurrent unit neural network configuration

2.5 门控循环单元神经网络结构配置与网络训练配置

经过多次实验评估，本文选择的网络模型配置如图6所示，具体网络配置说明如表2所示.整个门控循环单元神经网络共由六个网络层组成，各层每个时刻点输出数据维度分别为16,12,10,8,4,2.网络层1输入10个时刻的20维向量数据xi(i=1,2,…,10)，向量xi各维的数据意义如表1所示，每个时刻间隔周期为1 s.网络层2至网络层6的输入为相邻前一层的输出.最后一层网络层6输出最后一个时刻的数据，得到电堆1#电压、电堆2#电压的预测值.

在网络训练时需要选定损失函数和训练算法.本文使用均方差损失函数和小批量梯度下降算法.设置训练集数据的训练轮数为40，小批量梯度下降算法的批量大小B=64，对学习率α的调整采用RMSprop算法.RMSprop算法的梯度更新计算方法为[19]：

表1 燃料电池系统数据集

表2 门控循环单元神经网络配置说明

G1=(1-β)g1⊗g1

(12)

Gk=βGk-1+(1-β)gk⊗gk

(13)

(14)

(15)

θk+1=θk-Δθk

(16)

式中：α是初始学习率，β为衰减率，gk表示第k次迭代的梯度，θk表示迭代前的参数值，θk+1表示第k次迭代后的更新参数值.这里的运算均为按元素运算.本文设置α=0.001，β=0.9，ε=10-7.

在网络训练过程中，每轮训练完成后计算训练集和测试集的均方差损失函数和所有预测变量的平均绝对误差，均方差损失函数用于衡量网络训练的性能.平均绝对误差MAE可以衡量预测误差的大小，其计算方法为：

(17)

式中各量的意义同(7)式.

2.6 结果分析和残差阈值的确定

本文实验所用Python版本为3.7.10，TensorFlow-GPU版本为2.3.0.

图7为训练过程中在训练集和测试集上的均方差损失和平均绝对误差变化.随着训练集上训练轮次的增加，均方差损失和平均绝对误差呈逐渐减小趋势，网络训练到第27轮以后减小趋势变缓，均方差损失和平均绝对误差变化趋于平缓.第40轮训练完成后，训练集上的均方差损失和平均绝对误差分别约为 0.001 01 和 0.011 38，测试集上的均方差损失和平均绝对误差分别约为 0.001 32和 0.012 09.整个训练过程中，训练集和测试集上的均方差损失和平均绝对误差非常接近，经过40轮训练后门控循环单元神经网络已经能较好拟合燃料电池数据，网络具有很强的泛化能力.

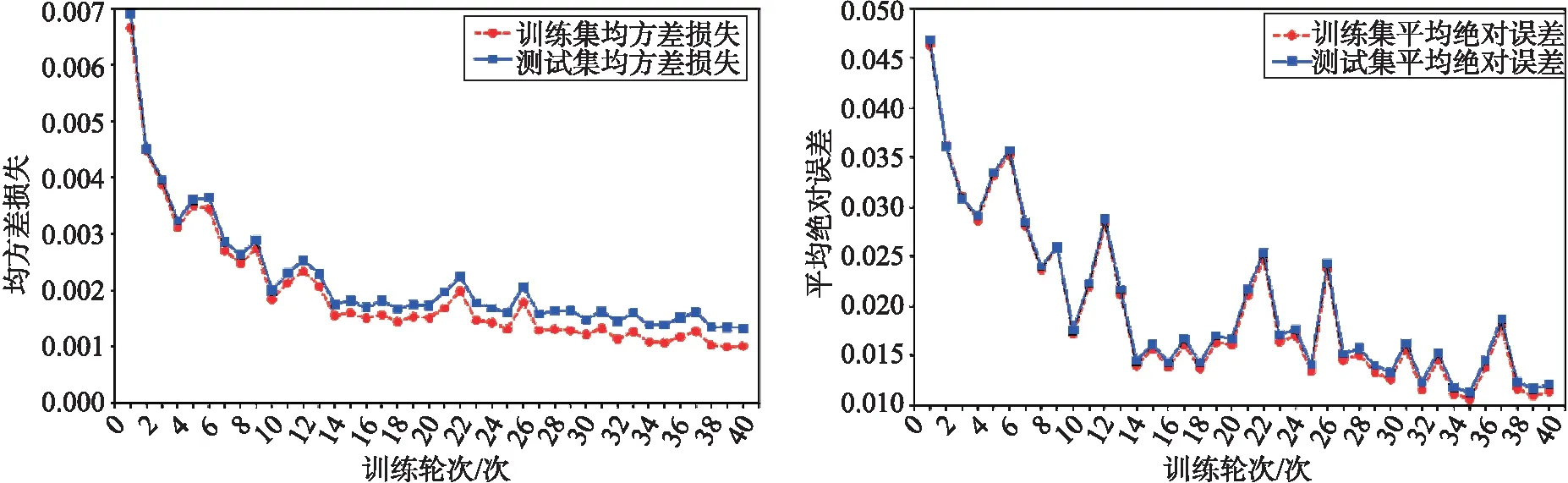
图7 训练集和测试集每轮训练均方差损失/平均绝对误差变化图(左图为均方差损失/右图为平均绝对误差)Fig.7 Mean squared error and mean absolute error versus epoch in training and test set (The left plot is mean squared error and the right plot is mean absolute error)

使用训练好的门控循环单元网络测试 8 600 个测试集样本，计算得到电堆1#电压预测误差均值和标准差分别约为μ1=0.000 29 和σ1=0.036 33，电堆2#电压预测误差均值和标准差分别约为μ2=-0.000 31 和σ2=0.036 24.计算结果表明测试集样本的预测误差的均值接近于0.图8和图9分别为网络在测试集上的电堆1#电压和电堆2#电压的预测误差.除了极少部分样本外，大部分样本的电压预测误差均在[-3σ1,3σ1]和[-3σ2,3σ2]误差带内分布.对极少部分预测误差不在误差带内分布的数据，推测有可能是样本数据错误造成的.

通过对预测误差的分析，设定电堆1#/2#电压残差阈值分别为R1th=3σ1=0.108 99、R2th=3σ2=0.108 72.在进行故障监测时，设定当电堆1#电压残差或电堆2#电压残差的绝对值超出阈值时即判定燃料电池系统运行出现故障.图10为采用门控循环单元网络分别对35组1#/2#电堆故障数据进行预测获得的电压残差，结果表明电压残差超出电压残差阈值，与燃料电池系统故障相符.

2.7 不同神经网络的比较

全连接神经网络是一种采用全连接层堆叠而成的神经网络，是一种广泛使用的网络.简单循环神经网络是一类基本循环神经网络，适用于处理序列信息.为对比不同网络的性能，本文分别对全连接神经网络和简单循环神经网络进行了实验，得到网络配置与训练测试结果如表3所示.全连接神经网络由于层与层之间采用稠密连接方式，参数量多，约是门控循环单元神经网络的8.5倍.由于网络层内部没有连接机制，全连接神经网络缺乏对序列信息的网络层内部提取能力.简单循环神经网络和门控循环神经网络一样，通过网络层内部的连接机制和网络层内部参数共享，提升了对序列信息的提取能力，降低了参数量.同时，由于网络层内的连接机制，简单循环神经网络在训练时可能出现梯度爆炸[19-20]或梯度弥散[20-21]现象.深层的简单循环神经网络训练较为困难.针对梯度爆炸和梯度弥散，本文分别采用梯度裁剪[20]方法和RMSprop算法[18]自适应调整学习率进行训练.梯度裁剪方法可以缓解梯度爆炸，同时也可能降低简单循环神经网络的训练效率.门控循环单元神经网络由于引入了门控机制，能很好地避免梯度爆炸和梯度弥散问题.

图10 1#/2#电堆故障电压残差(左图1#电压残差/右图2#电压残差;数据已归一化，纵轴为无量纲量)Fig.10 1#/2# stack voltage residual(The left plot is 1# voltage residual,and the right plot is 2# voltage residual; Variables in the vertical axis have been normalized and are dimensionless)

表3 几种不同神经网络的实验比较

3 结 论

本文针对质子交换膜燃料电池系统故障监测问题，采用神经网络拟合的方法建立质子交换膜燃料电池系统的输入输出数据模型.根据基于模型的监测方法进行实验得到以下结论：

1)基于燃料电池系统的运行数据，提出了采用门控循环单元神经网络建立燃料电池的黑盒模型模拟系统运行状态.通过预测系统电压输出进而利用电压残差监测系统运行状态，诊断系统运行状态有无故障.

2)门控循环单元神经网络的训练和测试结果表明，数据能较好模拟系统运行状态，所提出的模型具有很强的泛化能力，从而能应用于监测燃料电池的运行状态和诊断系统是否存在故障.

3)与全连接神经网络和简单循环神经网络的实验对比表明，门控循环单元神经网络具有兼顾网络参数量和训练难度适中的特点，具有组合优势.