基于不同机器学习算法的地震滑坡易发性评价<br/>——以鲁甸地震为例

基于不同机器学习算法的地震滑坡易发性评价
——以鲁甸地震为例

2022-05-07吉日伍呷田宏岭韩继冲

昆明理工大学学报(自然科学版) 2022年2期

吉日伍呷，田宏岭，韩继冲

(1.中国科学院、水利部成都山地灾害与环境研究所，四川成都 610041； 2.中国科学院大学，北京 100049； 3.中国科学院地表过程与山地灾害重点实验室，四川成都 610041；4.北京师范大学地理科学学部，北京 100875)

0 引言

在地震活跃的山区，由地震引发的滑坡是重要的次生灾害之一，滑坡对人类的生命财产造成了严重的破坏[1].已有研究统计表明，2004年到2010年间发生了 47 736 起地震引发的山体滑坡伤亡事件[2].有时地震引发的山体滑坡造成的生命和财产损失超过地震造成的损失[3].滑坡在地貌和地质灾害演变中起着重要作用[4].中国西南山区与青藏高原东缘相接，是地震和滑坡灾害发生的热点地区.因此，及时准确地对地震引发的滑坡的易发性进行评价有利于减少灾害带来的损失.

目前，滑坡易发性地图绘制方法可分为两种：定性和定量方法.在定性方法中，一般根据专家意见指定评价指标的权重，例如层次分析法[5]，这种方法较为主观.定量的方法一般从数据中挖掘信息，可以将其视为相对客观的方法.定量的方法包括频率比[6]、信息量模型[7]、MaxEnt模型[8]、Newmark模型[9]和机器学习方法等.机器学习方法又包括逻辑回归、随机森林、K近邻、贝叶斯、C5.0决策树、支持向量机和神经网络等[10-12].基于机器学习方法对滑坡易发性进行评估是目前该领域的研究热点之一[3].与传统的统计模型不同，机器学习模型旨在做出最准确的预测，而传统的统计模型旨在推断变量之间的关系[13].这些方法可作为评估滑坡易发性的有用工具，还可用于评估不同因素对滑坡发生的影响.例如，马思远等人[12]基于逻辑回归模型对九寨沟地震滑坡的危险性进行了评估；胡安龙等人[14]基于贝叶斯算法对滑坡的稳定性预测进行了研究；吴润泽等人[11]基于随机森林算法对三峡库区湖北段的滑坡易发性进行了评价.这些研究大多基于单一的机器学习方法，缺乏不同机器学习方法的精度对比.由于不同机器学习方法的原理不同，预测精度可能存在较大差异.因此，为了更准确地评估地震滑坡的易发性，有必要对目前应用较为广泛的几种机器学习方法在地震滑坡易发性评估中的性能进行对比.

本文以鲁甸Ms6.5级地震作为研究案例，首先构建评价指标体系，然后选择了四种常见的机器学习算法构建预测模型，基于不同的精度评价指标对比这些模型在地震滑坡易发性评估中的性能.最后，基于随机森林模型分析了不同评价指标的相对重要性.本文的研究结果可为评价指标的选择和未来地震滑坡易发性建模工作提供一定的参考.

1 研究区与数据

1.1 研究区

本文以2014年8月3日云南省鲁甸县发生的Ms6.5级地震作为研究案例(图 1).本文中的研究尺度为区域尺度，面积约为 2 590 km2.鲁甸地震的震中位于103°20′24″E, 27°6′0″N(中国地震台网).已有统计表明，鲁甸地震中共造成617人死亡，112人失踪和 3 143 人受伤[15]，人员伤亡和经济损失严重.此次地震造成了大量的山体滑坡，例如最大的红石岩滑坡(103°24′0″E, 27°2′16.8″N)，体积约为12.24 Mm3[16].与其他地方发生的地震相比，鲁甸地震引发了更多数量和种类的滑坡[17].因此，对该地区的地震滑坡易发性进行建模具有典型性.

1.2 数据来源与处理

1)滑坡编录数据.本文使用的研究区内的地震引发的滑坡数据来源于已有的滑坡编录数据库[18]，滑坡数据集由吴玮莹等人[19]制作完成.该滑坡编录数据主要由实地调查和基于地震发生后的高分辨率的卫星影像目视解译完成，数据具有较高的质量和完整性.本文参照已有的研究方法[2]，在ArcGIS中生成等量的非滑坡点.最后，将滑坡和非滑坡点分别按照7∶3的比例进行随机划分[11]，得到用于训练机器学习模型的训练数据集(1 434 个样本点)和用于验证模型的预测精度的测试数据集(614个样本点).

2)地震动参数数据.本文中使用的地震动参数包括修正的麦加利地震烈度(Modified Mercalli Intensity, MMI)，MMI表示不同地区产生的地面震动强度，该指标被认为是客观和准确的.MMI以地震记录数据为基础，地面震动严重程度随着MMI等级的提高而增加.本文使用的数据来源于美国地质调查局的ShakeMap数据集.需要注意的是ShakeMap数据的准确性可能会影响滑坡易发性的预测精度.

3)地形数据.数字高程数据(Digital Elevation Model, DEM)来源于美国NASA的航天飞机雷达地形任务(SRTM V4).基于DEM在SAGA中计算得到地形坡度、曲率和地形湿度指数[1]的空间分布.地形湿度指数(Topographic Wetness Index，TWI)的计算公式如下：

(1)

式中：a表示网格单元排水的局部上坡集水区，b表示坡度.

4)断层和岩性数据.本文中研究区使用的断层数据来源于GEM全球活动断层项目的断层数据集(https://github.com/GEMScienceTools/gem-global-active-faults).然后在ArcGIS中使用欧式距离工具生成距断层距离的空间分布图.岩性数据来源于GLiM 全球岩性数据集[20].

5)水文和植被数据.本文使用的水文数据为研究区的河流矢量数据，在ArcGIS中使用欧式距离工具生成距河流距离的空间分布图.此外，本文还基于最大值合成法和Landsat卫星影像得到了研究区地震发生前五个月内的归一化植被指数最大值(Normalized Difference Vegetation Index, NDVI)，其中Landsat影像由CFMASK(The C Function of Mask)算法去除云和阴影区域.

2 构建评价指标体系

图2 地震滑坡易发性评价指标空间分布Fig.2 Spatial distribution of evaluation indexes of earthquake landslide susceptibility

基于数据的可获取性和参照前人的研究[1, 11-12, 21]，本文从地震动参数、植被、断层岩性、水文和地形方面构建了地震滑坡易发性评价指标体系(图2).(1)MMI：地震动参数是引发滑坡的关键因素，MMI能够反映地面震动的特性[1].(2)NDVI：该指标代表了植被覆盖率，而覆盖率会影响土壤-植被根基的复合强度，从而影响边坡的稳定性[11].(3)距断层距离：发生地震时，断层周围容易发生滑动，岩石的稳定性差，滑坡经常发生在断层处[22].(4)岩性：不同的岩性单元对滑坡的发生有不同的影响，低强度的岩石类型易于滑落且岩石的易蚀程度影响着侵蚀和风化过程[21].(5)距河流距离：该评价指标反映了河流侵蚀山坡的能力，河流的侵蚀作用是滑坡的主要成因[10].(6)高程：海拔高度会通过控制植被和地理环境来影响边坡的稳定性[12].(7)坡度：该指标是影响滑坡稳定性的重要因素，随着坡度角的增加，滑坡发生的频率显著增加[22].(8)TWI：它显示出斜坡的湿度和流动模式，可以较好地描述地形变化对土壤径流的影响[1].(9)曲率：描述了地形的形态，影响沉积和侵蚀的速度[21].

在训练机器学习模型之前，需要对评价指标进行共线性检验.本文计算了滑坡点的各评价指标间的皮尔逊相关系数(r)和显著性，若相关系数的绝对值大于0.7，则应剔除相关指标[23].共线性检验是使用R语言完成的，其中相关系数由“cor”函数计算得到，显著性检验由“cor.mtest”函数计算得到.相关性结果表明，不同指标间的相关系数均小于0.7，这表明指标间不存在共线性，满足用于模型训练的数据要求.

3 方法

3.1 机器学习算法

1)逻辑回归(LR)

逻辑回归是一种适用于多变量控制的广义线性回归分析模型，其是滑坡易发性建模中广泛应用的模型之一[24].逻辑回归模型与常见的线性回归模型不同，其通过Sigmoid函数将输出值限制为区间[0，1].本文中使用的逻辑回归方程中的参数估计方法为点估计.该算法的具体公式可参考文献[12].

2)K近邻(KNN)

K近邻方法是一种基于实例的学习方法，输入由特征空间中的k个最接近的训练实例组成，实例被分配到所选近邻中最频繁的类.本文中使用中等KNN算法的邻点个数为10，距离度量选择Minkowski，该算法的具体原理可见参考文献[25].K近邻目前已在包括滑坡易发性地图绘制在内的许多领域中使用[25].

3)朴素贝叶斯(BAYES)

朴素贝叶斯分类器是基于贝叶斯定理的分类系统，该算法假设所有属性在给定输出类别的情况下都是完全独立的，具体原理可见参考文献[26].本文中的贝叶斯算法的数值预测变量分配了高斯分布.该算法的主要优点是它很容易构造，不需要任何复杂的迭代参数估计方案.

4)随机森林(RF)

随机森林是由Breiman在2001年开发，其使用多颗树进行预测分类，最后通过投票得到最终的预测结果[27].该方法已广泛应用于许多领域，并取得了较好的效果.与其他机器学习模型不同，RF提供了衡量指标变量相对重要性的度量、袋外数据错误率和基尼指数.本文中随机森林算法的最大分裂数为 1 433.

本文在不同机器学习模型预测的地震滑坡发生概率是通过每个网格单元中的模型输出(在0到1之间)来估计的，并以0.5的概率作为划分滑坡和非滑坡的阈值.上述4种机器学习算法在Matlab的Classification Learner中实现.

3.2 精度评价

为更加客观地对比不同机器学习模型的地震滑坡预测性能，参照前人的研究[28]，本文使用了五项指标进行精度评价，包含精确度、灵敏度、准确度、接受者操作特性曲线(Receiver Operating Characteristic curve，ROC)和ROC曲线下的面积(Area Under Curve，AUC)值.精确度表示预测为预测正确的滑坡数量占实际滑坡数量的比例；灵敏度表示预测正确的滑坡数量占预测为滑坡总数量的比例；准确度同时兼顾了滑坡和非滑坡预测结果的精度.

(2)

(3)

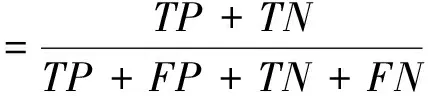
(4)

式中：FP表示将非滑坡错分为滑坡的样本数量，FN表示将滑坡错分为非滑坡的样本数量，TP表示正确预测为滑坡的样本数量，TN表示正确预测为非滑坡的样本数量.

4 结果

4.1 模型精度对比

基于上述方法，得到了不同机器学习模型在测试数据集上的预测精度(表1).对比发现，四种机器学习方法中，基于RF模型中有20个非滑坡样本错分为了滑坡，17个滑坡样本错分为了非滑坡，其灵敏度(0.94)、精确度(0.94)和准确度(0.94)均高于另外3种机器学习模型.此外，本文发现BAYES和KNN模型均具有较高的灵敏度(分别为0.93和0.92)和较低的精确度(分别为0.85和0.88)，这表明BAYES和KNN模型均高估了滑坡发生的概率，即将更多的非滑坡预测为了滑坡，且BAYES比KNN模型高估程度更高.同时，本文发现虽然LR、KNN和BAYES模型的准确度几乎相同(分别为0.89,0.90和0.89)，但LR模型的灵敏度(0.90)和精确度(0.89)相差较小，这表明LR模型在滑坡和非滑坡的预测精度较为平衡.

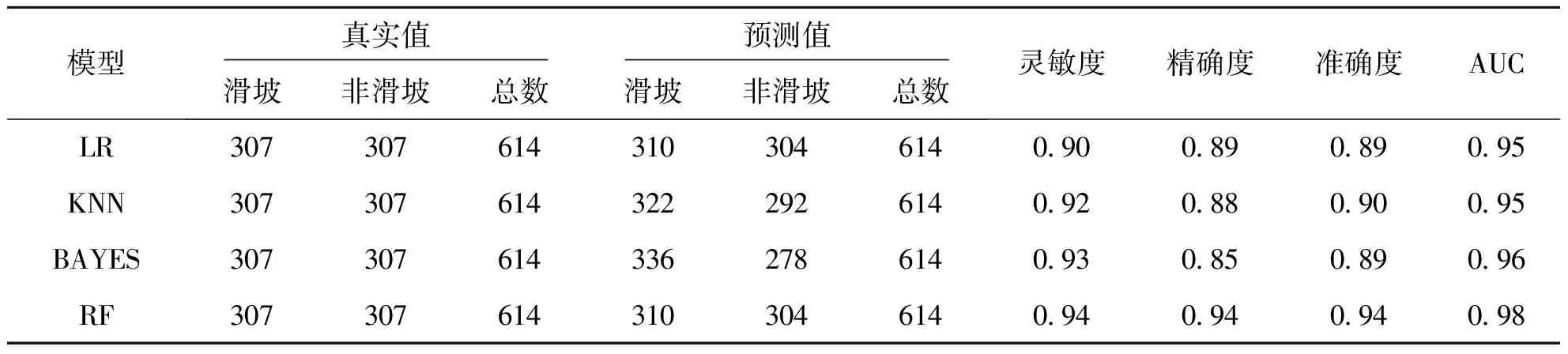
表1 不同机器学习模型的混淆矩阵和精度评价

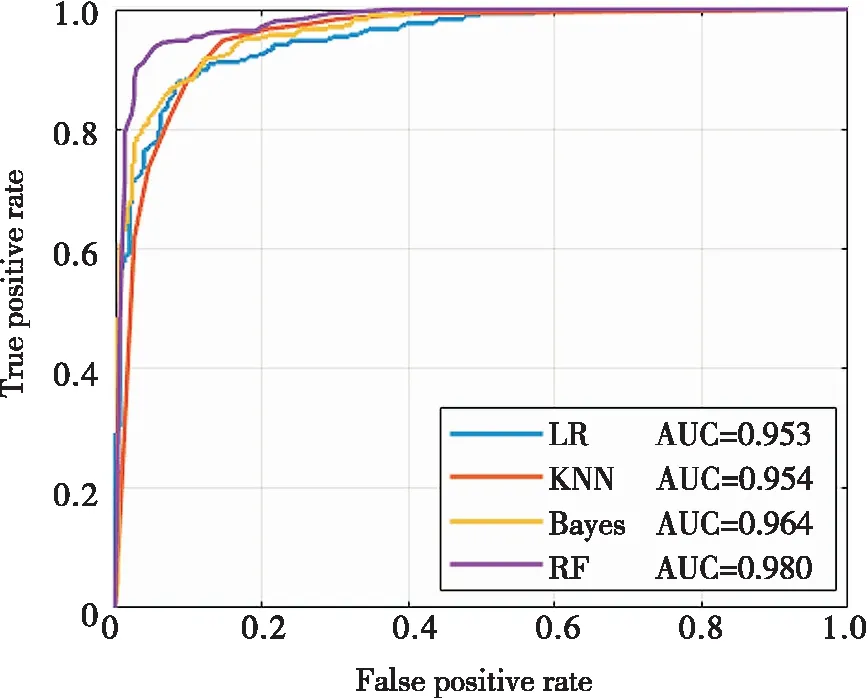
图3 不同机器学习模型预测结果的ROC曲线和AUC值Fig.3 ROC curve and AUC value of the prediction results of different machine learning models

ROC曲线结果(图3)显示：LR，KNN和BAYES模型的曲线相似，而RF模型的ROC曲线更加接近于1，表现更好.此外，RF的AUC值(0.98)相比另外三种机器学习模型也更高.综合分析表明，RF是在地震滑坡预测中性能最好的模型，BAYES模型预测精度相对较差.

4.2 地震滑坡易发性制图

图4显示了四种机器学习模型的地震滑坡易发性空间预测结果.BAYES模型的易发性结果明显高估了滑坡的发生概率.RF模型预测的易发性地图与实际滑坡的发生位置最为相符，滑坡发生的区域位于RF模型预测的高发生概率地区.LR和KNN的易发性制图结果误差相对较小.此外，不同模型预测结果的概率范围与实际发生的滑坡数量的统计结果显示(表2)：RF模型的结果中，随着滑坡发生概率的升高，像元个数逐渐减少，而实际发生的滑坡数量逐渐升高，且位于预测概率大于0.5、0.7和0.9的区域的实际滑坡数量分别占总实际滑坡数量的97.36%、92.66%和74.07%.对比LR、KNN模型可以发现，虽然RF模型预测概率在0.9～1的像元个数最少，但包含的实际滑坡数量最多，分别比LR和KNN多152和148个.这更加证明了随机森林在地震滑坡易发性制图中的准确性.此外，虽然BAYES预测结果中的滑坡发生概率在0.9～1的范围内包含的滑坡个数比RF模型多，然而其在该区间的像元数却远大于RF模型.综合分析表明，RF模型的地震滑坡易发性制图结果更加符合实际情况.

图4 不同机器学习模型预测的地震滑坡易发性空间分布图Fig.4 The spatial distribution map of earthquake landslide susceptibility predicted by different machine learning models

表2 不同机器学习模型的滑坡易发性等级的像元和实际滑坡数量统计

4.3 指标相对重要性评价

基于随机森林模型对不同指标在地震滑坡易发性建模中的相对重要性进行了评价.两种相对重要性评价的依据分别为袋外数据错误率(图5左图)和基尼指数(图5右图)[3].结果表明，两种评价标准下，不同指标对模型建立的相对重要性排序结果相似，距河流距离、MMI、距断层距离和坡度为相对重要的评价指标.MMI在袋外数据错误率和基尼指数的排名中，分为位于第一位和第二位.先前的研究也表明，在地震引发的山体滑坡中，地震动参数是评估边坡稳定性的良好和可靠的标准，是最重要的影响因素之一[29].因此，在未来的滑坡易发性建模中，不应忽视地震动参数的作用.

图5 基于随机森林模型的评价指标相对重要性Fig.5 Relative importance of evaluation indicators based on random forest model

5 讨论

目前，人工智能技术不断发展，机器学习是人工智能中发展最快的分支之一，统计机器学习模型建立在统计框架之上.然而部分模型仍然存在争议，例如逻辑回归模型.部分研究认为逻辑回归属于统计学模型[25-26]，也有一些研究将其作为机器学习模型中的一种[6].本文将逻辑回归放在了机器学习模型中，主要有以下观点.(1)统计学是从样本中得出总体推论，统计建模更多地是寻找变量之间的可解释关系[13].虽然有很多统计模型也可以进行预测，但预测结果的准确性并不是它们的强项.相比之下，机器学习专注于预测，其依靠已有的数据经验找到可概括的预测模式，但对模型的可解释性关注相对较弱.本文使用逻辑回归建立专注于滑坡预测结果的准确性，我们不需要知道关于滑坡与各变量之间测量的具体机理细节.(2)监督机器学习技术通过为模型提供可以从中学习的输入输出样本数据，来训练模型，该学习过程称为模型的“训练”，训练过程可能涉及重复的更新参数.模型训练好之后，需要使用新的数据来验证模型学习或预测的性能.在传统的统计模型中，其通过使用参数检验等指标来检查模型情况，所以两者的评估程序存在差异[30].从这种角度看，本文中的逻辑回归是一种监督机器学习模型，因为它使用已有的70%的样本数据作为训练集来训练模型，并使用其余30%新的样本数据作为测试集来验证模型的预测性能.(3)此外，目前许多主流的编程语言中的机器学习库或软件将逻辑回归分类为机器学习模型.例如Python编程语言中的Scikit-learn机器学习库，MATLAB软件中的Classification Learner机器学习分类算法APP，以及数据挖掘软件Weka.总的来说，统计学模型和机器学习模型在某些方面可能是互补的，随着理论和技术的发展，该问题仍需要更加深入的讨论.