受固定约束物体运动情境分析的策略

安徽 邵 永 侯朝阳

受固定约束的运动是一种常见的运动，对于典型的受约束的运动，例如轻绳、轻杆约束下的圆周运动等是教学的重点内容，已经有较为丰富的分析和总结，学生对此的理解也比较深刻，而对于一些非典型的受固定约束的物体运动，学生的认识往往不深刻、把握不准确，分析问题、解决问题时较为困难。实际上无论是典型的还是非典型的受约束运动的分析都要抓住受约束这个特点。

一、对安徽省示范高中培优联盟2021年秋季联赛第13题的思考

图1

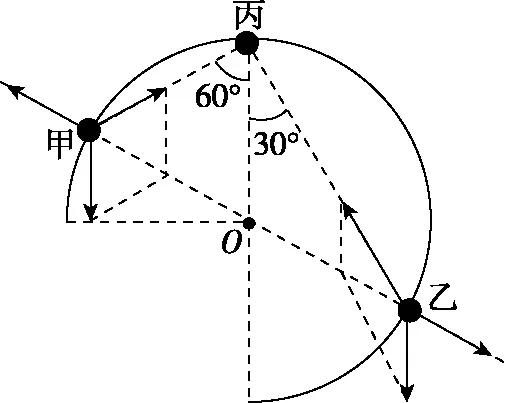
图2

如果甲、乙球与圆环间有作用力，两小球的质量是否还是相等的关系呢？由于圆环对小球的作用力属于外力，如果还使用上述的这两种分析方法都需要先分析支持力，由于受到圆轨道的约束，我们不妨根据受约束的特点，从切线方向用力的分解试试。

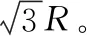
二、约束轨道固定不动模型两例

【例2】如图3所示，一颗珠子穿在一个固定在竖直平面、半径为R的圆环上，可以沿着圆环自由滑动。现用一个轻质橡皮筋连接圆环最高点和珠子，初始时刻珠子静止于圆环最低点，此时圆环作用在珠子上的力为其重量的两倍。轻轻拨动珠子，珠子开始沿着圆环向上滑动，当它滑过三分之一圆周时动能达到最大。试求完全放松后橡皮筋的长度。

图3

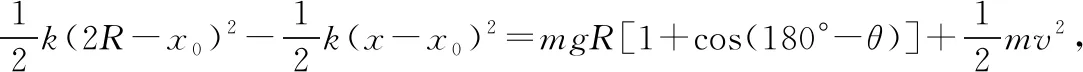
【例3】如图4所示，一光滑绝缘斜面ABC，斜面长为L(∠BAC=90°)，D为BC上的点，BC与AD垂直。A处固定一带电荷量为+q、质量为m的小球，另一同样带电小球自B点由静止释放，球能沿斜面从B点运动到斜面底端C处，则小球从B点运动到C点的过程中速度如何变化。

图4

【解法一】数学不等式在极值问题中的应用

【解法二】导数在极值问题中的应用

【解法三】约束条件在分方向中的应用

【点拨】临界和极值问题是物理试题中的重点也是难点，常用的求极值方法有配方法、三角函数法、不等式法、Δ判别式法、求导法等等，由于在初始运动阶段库仑力变大，夹角的余弦值变小，库仑力沿斜面的分力不易判断，所以通过物理情境的分析，求出其解析式，通过数学方法讨论其极值，这是符合理性思维的，这样讨论能解决问题，但对学生的数学能力的要求太高，由于这是约束性的运动，所以一定要满足约束性的条件，才能从约束条件入手，快速分析问题。

三、约束轨道运动模型两例

(1)带电小球从管底到飞出管口时所用的时间是多少；

(2)带电小球离开磁场时的位置到坐标原点的距离是多少。

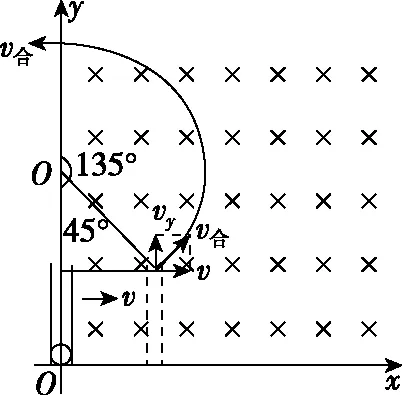
图6

【点拨】由于小球随玻璃管一起向右运动的同时还沿管运动，所以其速度的大小和方向均是不断变化的，小球所受洛伦兹力的大小和方向也是不断变化的，因此小球的运动是复杂的。如果把洛伦兹力分解为沿管方向的分力和沿x轴方向的分力，由于小球在x轴方向做的是匀速运动，所以洛伦兹力沿管的分力大小恒定不变，根据独立性，可得小球沿管方向做匀加速运动；沿管的速度增大引起洛伦兹力向左的分力变大，通过逐渐增大的外力的作用保证管在水平方向做匀速运动。

【例5】如图7所示，半径R=0.3 m、质量M=1 kg的半圆形滑槽，静止放置在水平地面上，一质量m=0.5 kg的小球从滑槽的右边缘与圆心等高处由静止滑下。不计一切摩擦，小球可看成质点，重力加速度大小g=10 m/s2，求小球滑至最低点时滑槽对它的支持力？

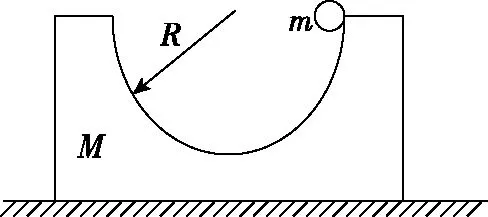
图7

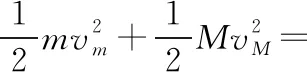
【点拨】当小球下滑至最低点时，由于圆形滑槽在运动，所以小球相对于地面不是做圆周运动，相对于滑槽才是圆周运动，支持力和重力的合力改变小球的方向，使之未做离心运动，所以在圆周运动的向心力公式中必须使用相对于滑槽的速度。

四、总结

受约束的运动是一种常见类型，它具有特殊性，从约束特点入手，利用分运动中力和运动的关系或两个分方向间的联系，往往可以使运动情境更清晰，问题的把握更准确、问题的解决更简便，是一种因地制宜、行之有效的研究策略。