一题多变,提高思维能力
2022-05-07■胡彬
■胡 彬
平行关系是立体几何中点、直线、平面位置关系的重点,是历年高考绕不开的一个考点,所以同学们要高度重视,还要全面掌握。下面通过一题多变方式的训练,进一步拓展同学们的思维,从不同角度加深对平行关系问题的认识。
题目 如图1 所示,在斜三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的中点。
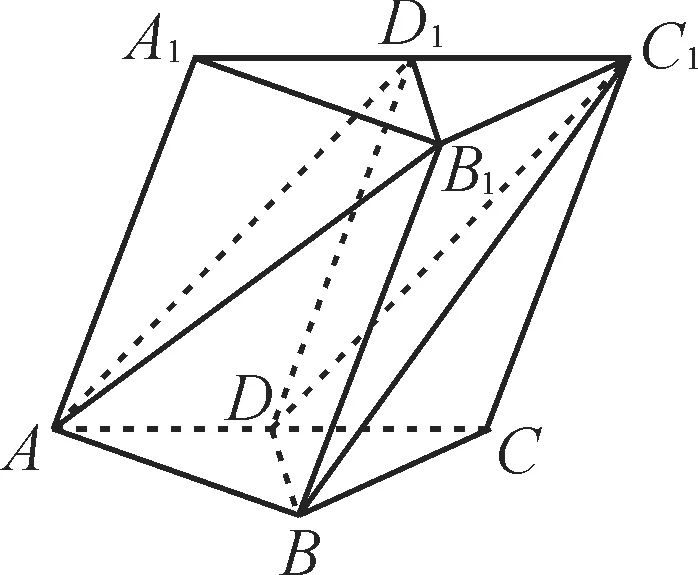
图1
(1)证明:AD1//平面BDC1。
(2)证明:BD//平面AB1D1。
思路分析:本题的两问都是证明线面平行,证明线面平行有一种非常重要的转换思想,就是把线面平行转换为面面平行。本题的两问都可以通过这种方式来证明。当然,最直接的方法就是证明直线与平面内的一条直线平行。
证明:(1)由D1,D分别为A1C1与AC的中点,四边形ACC1A1为平行四边形,可得C1D1//DA,且C1D1=DA,所以四边形ADC1D1是平行四边形,所以AD1//C1D。
又AD1⊄平面BDC1,C1D⊂平面BDC1,所以AD1//平面BDC1。
(2)由BB1//平面ACC1A1,BB1⊂平面BB1D1D,平面ACC1A1∩平面BB1D1D=D1D,可得BB1//D1D。
因为D1,D分别为A1C1,AC的中点,所以BB1=DD1,所以四边形BDD1B1为平行四边形,可得BD//B1D1。
又BD⊄平面AB1D1,B1D1⊂平面AB1D1,所以BD//平面AB1D1。
证明直线与平面平行,一般有三种方法:利用定义直接判断,一般用反证法;利用判定定理证明,关键是在平面内寻找一条直线与已知直线平行;利用两平面平行的性质,即两平面平行,其中一个平面内的任意直线都平行于另一个平面。

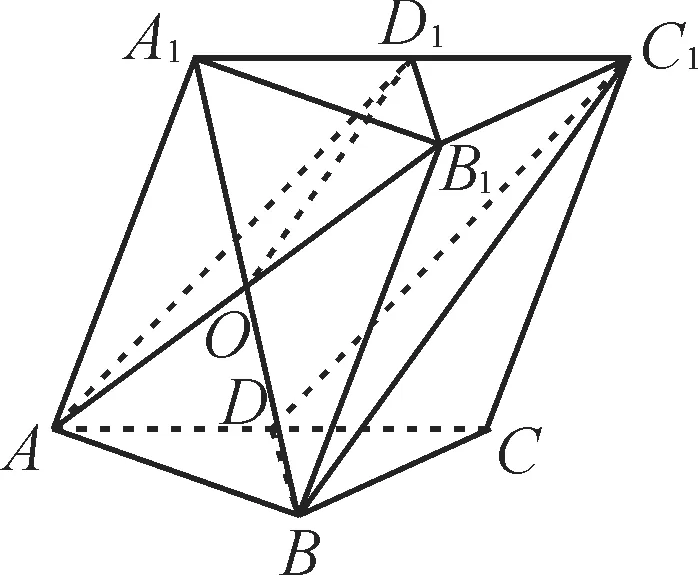
图2
由棱柱的性质知四边形A1ABB1为平行四边形,可得O为A1B的中点。
在△A1BC1中,点O,D1分别为A1B,A1C1的中点,所以OD1//BC1。又OD1⊂平面AB1D1,BC1⊄平面AB1D1,所以BC//平面AB1D1。
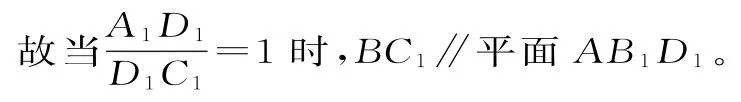
由于棱柱的侧面都是平行四边形,侧面的对角线相互平分,于是取A1C1的中点,就可得到平面AB1D1内的直线与BC1平行。

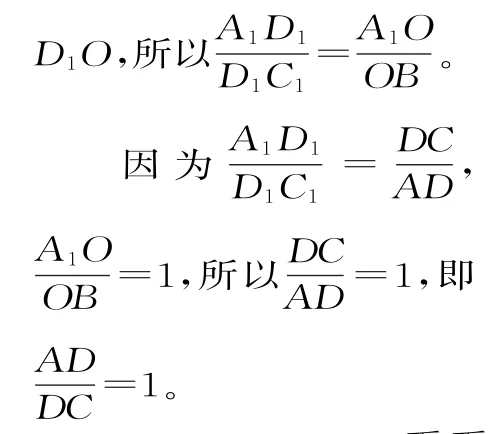
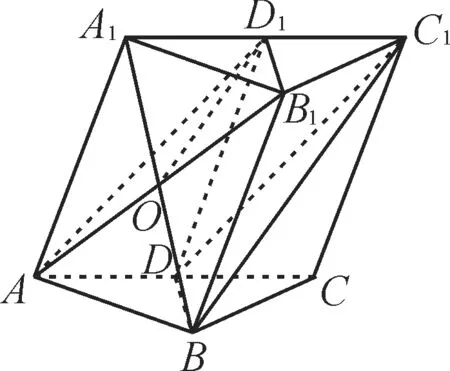
图3
面面平行的一个重要性质:两个平行平面与第三个平面相交,则交线平行。由此性质可确定两条平行直线,从而得到相应线段的比例关系。
