例说与球有关的切、接问题
2022-05-07谭先美
中学生数理化·高一版 2022年4期
■谭先美
与球有关的切、接问题是高考命题的热点,也是同学们学习的难点。为了更好地学好这部分内容,下面归纳几种常见题型,供同学们学习与参考。
一、锥体的外接球问题
例1 已知正四面体ABCD的棱长为2,E,F,G分别为AB,BC,CD的中点,则正四面体ABCD的外接球被平面EFG所截的截面面积是( )。
解:将正四面体ABCD放入正方体中,如图1所示。
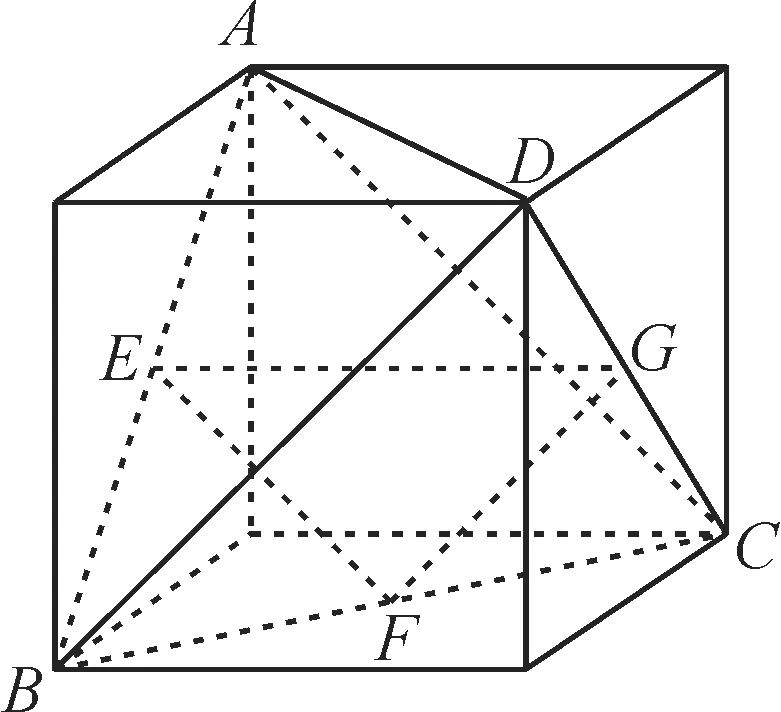
图1
因为E,G分别为AB,CD的中点,所以E,G分别为左右侧面的中心,所以正方体的外接球即为正四面体的外接球,其球心为线段EG的中点,所以正四面体ABCD的外接球被平面EFG所截的截面即为大圆。



二、柱体的外接球问题
例2 已知圆柱的高为1,它的两个底面的圆周在直径为2 的同一个球的球面上,则该圆柱的体积为( )。

评注:所有圆柱都有外接球,其球心是上下两底面圆的圆心连线的中点。
三、台体的外接球问题

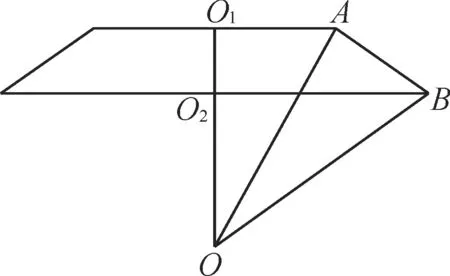
图2

四、锥体的内切球问题

解:如图3,过点P作PD⊥平面ABC于点D,AD的延长线交BC于点E。
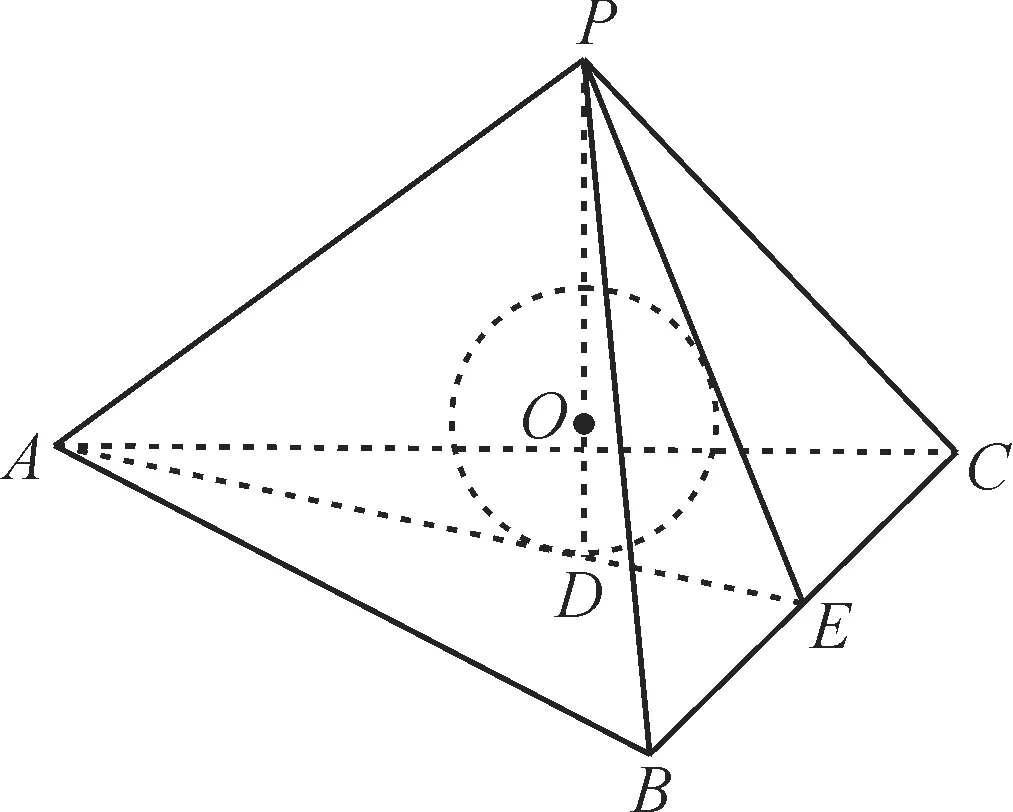
图3
在正三棱锥P-ABC中,因为△ABC是正三角形,所以AE是BC边上的高和中线,D为△ABC的中心,PD为正三棱锥的高,内切球的球心O在正三棱锥的高上。

五、柱体的内切球问题

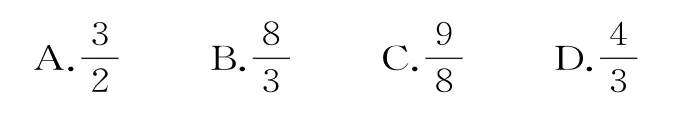
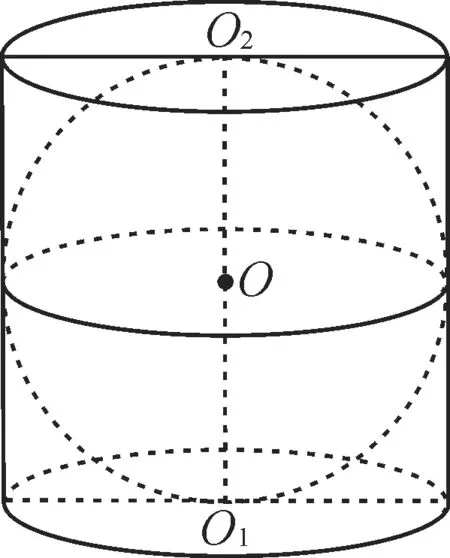
图4

