小议折叠问题
2022-05-07■姚洁
■姚 洁
平面图形的折叠问题是高考的常考题型,解答这类问题的关键是要分清折叠前后图形(折叠前的平面图形和折叠后的空间图形)的各元素间的位置关系和数量关系。
一、折叠成四面体求体积
例1 将长、宽分别为4 和3 的长方形ABCD沿对角线AC折成二面角,得到四面体A-BCD,则四面体A-BCD的外接球的体积为____。

评注:求球的体积的关键是根据已知条件以及图形的性质找到球心,确定球的半径。
二、折叠成正方体,求异面直线所成的角
例2 一个正方体的展开图如图1 示,A,B,C,D为原正方体的顶点,则在原来的正方体中,AB与CD所成的角为( )。
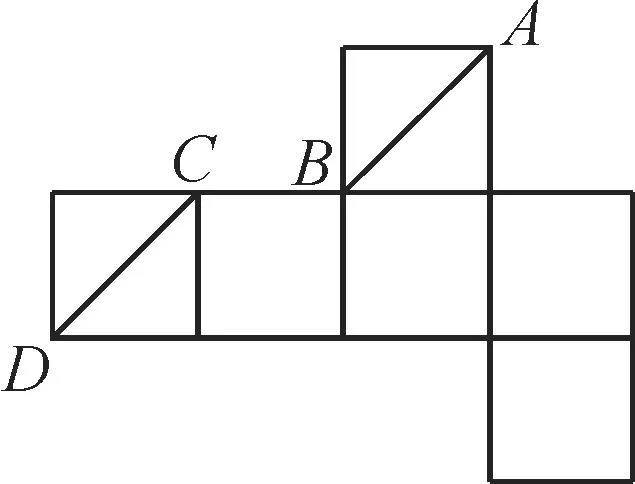
图1
A.30° B.45°
C.60° D.90°
解:把展开图中的各正方形按图2 所示的方式分别作为正方体的前、后、左、右、上、下面还原,得到图3所示的直观图。
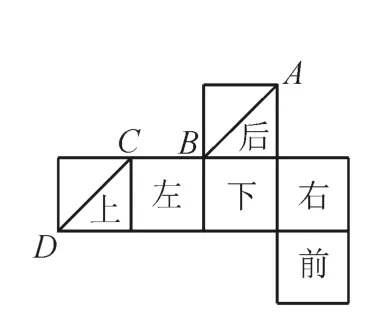
图2
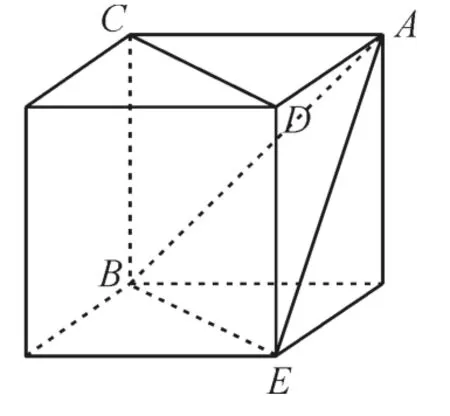
图3
在图3 中,因为BE//CD,所以∠ABE就是AB与CD所成的角。因为△ABE为等边三角形,所以∠ABE=60°。应选C。
评注:判断异面直线的两种方法:判定定理法,平面外一点与平面内一点的连线和平面内不经过该点的直线是异面直线;反证法,证明两直线不可能平行、相交或证明两直线不可能共面,从而可得两直线异面。
三、折叠成四棱锥,证明面面平行
例3 如图4,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE。若M为线段A1C的中点,N为DC的中点,则在△ADE翻转过程中,平面A1DE与平面MNB的位置关系是( )。
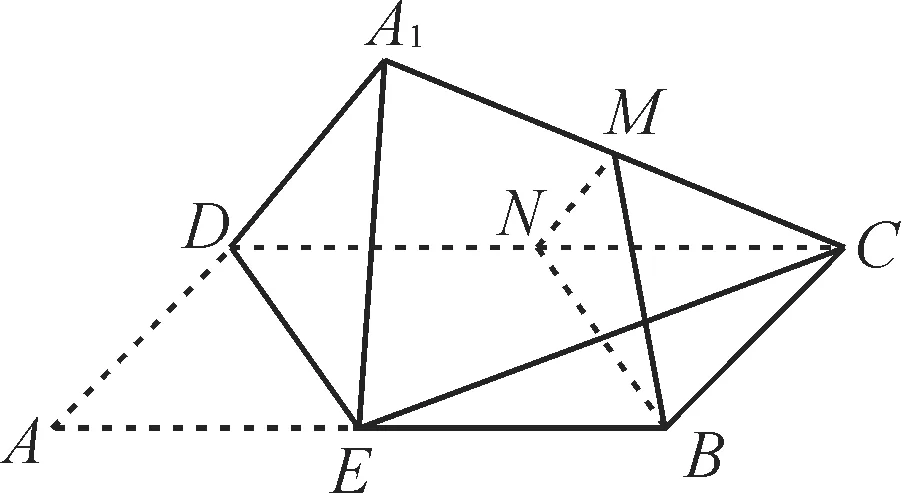
图4
A.垂直 B.相交不垂直
C.平行 D.无法确定
解:因为M为线段A1C的中点,N为DC的中点,所以MN//A1D。因为MN⊄平面A1DE,A1D⊂平面A1DE,所以MN//平面A1DE。同理可得,NB//平面A1DE。
又因为MN∩NB=N,所以平面MNB//平面A1DE。应选C。
评注:证明面面平行的五种常用方法:利用面面平行的定义;利用面面平行的判定定理,如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行;利用垂直于同一条直线的两个平面平行;两个平面同时平行于第三个平面,那么这两个平面平行;利用“线线平行”“线面平行”“面面平行”的相互转化。
四、折叠成三棱锥,证明线面垂直
例4 如图5,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G。现给出下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF。
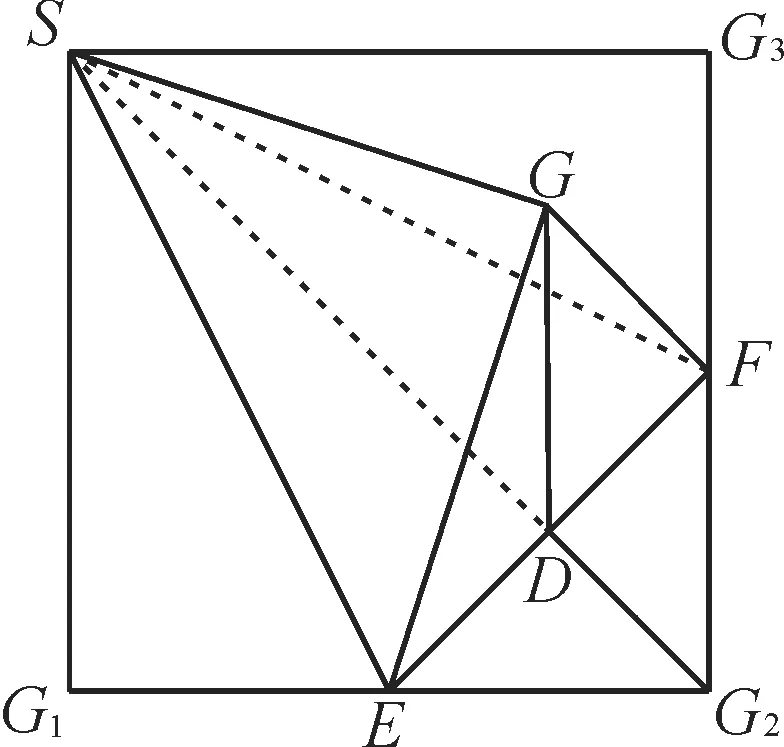
图5
其中正确的结论是( )。
A.①③ B.②⑤ C.①④ D.②④
解:因为在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,所以SG⊥GE,SG⊥GF,可得SG⊥平面EFG,①正确,②错误。因为SG⊥GF,SG⊥GD,所以GF不垂直于SF,GD不垂直于SD,即GF不垂直于平面SEF,GD不垂直于平面SEF,③⑤错误。因为EF⊥GD,EF⊥SG,GD∩SG=G,所以EF⊥平面GSD,④正确。应选C。
评注:证明线面垂直的三种常用方法:利用线面垂直的定义,直线a与平面α内的任何直线都垂直,则a⊥α;判定定理1,m,n⊂α,m∩n=A,l⊥m,l⊥n⇒l⊥α;判定定理2,若a//b,a⊥α,则b⊥α。
五、折叠成四棱锥,求直线与平面所成角
例5 如图6,在平面五边形EABCD中,已知BCDE是边长为4 的正方形,△ABE是正三角形。
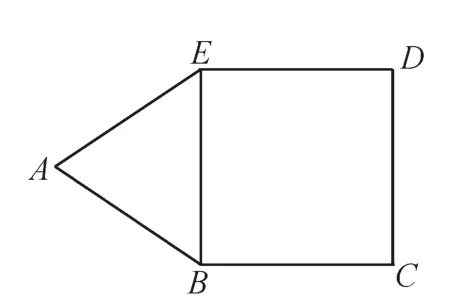
图6
把△ABE沿BE折起得到四棱锥A-BCDE,使得点A在平面BCDE上的投影是正方形BCDE的中心(如图7),则AB与平面BCDE所成角的正切值是____。
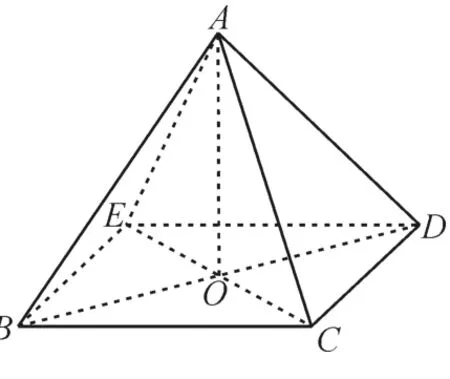
图7
解:依题意可知,把△ABE沿BE折起,使得点A在平面BCDE上的投影是正方形BCDE的中心,则得到的四棱锥A-BCDE是正四棱锥。

评注:求直线与平面所成角就是求直线与平面的射影所成的角,一般需要把直线与平面所成的角转化到一个三角形中进行求解。
如图8,已知PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点。
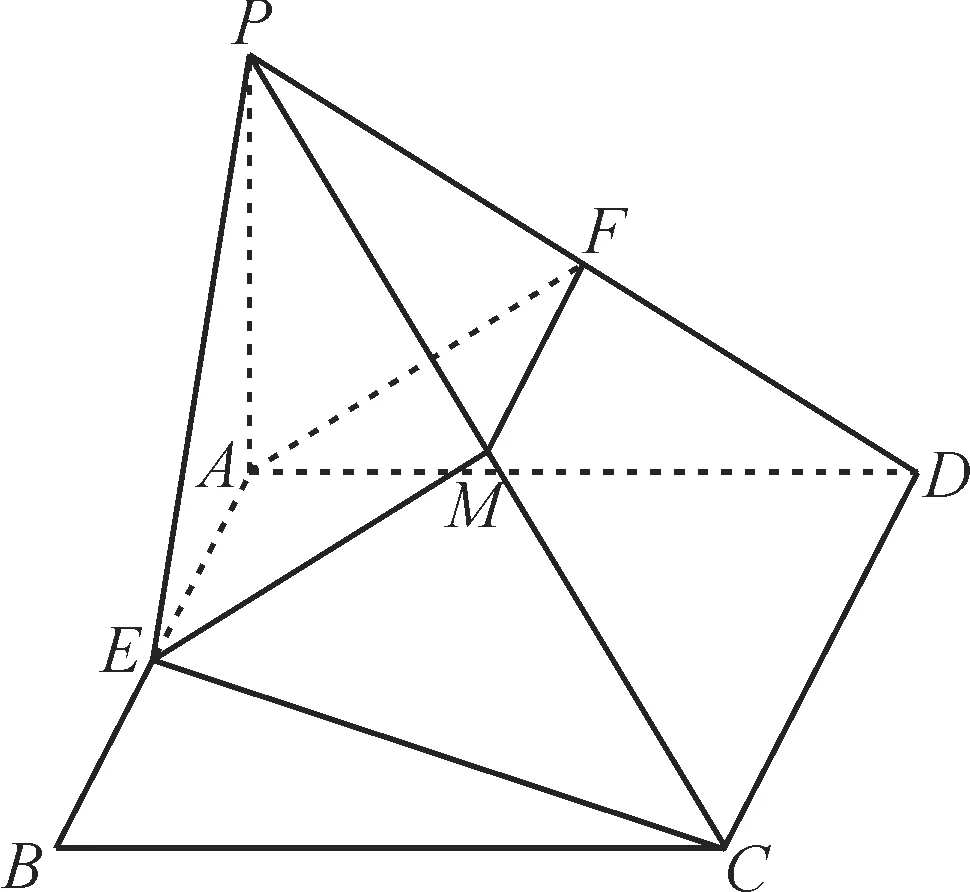
图8
求证:AF//平面PCE。

