一种基于ALD的贝叶斯分位数回归估计

韦学永,金良琼,沈婷,朱伟业成

(贵州民族大学 数据科学与信息工程学院,贵州 贵阳,550025)

自最小二乘回归估计被提出后,其应用就遍及社会经济的各个领域,但它只考虑了条件均值下因变量与自变量之间的关系,而在实际的应用中,有时需要分析数据的各个分位点下因变量与自变量之间的关系,因此1978年Koenker等第一次提出了“分位数回归”的概念,补充了基于最小二乘估计对只关注条件均值估计的不足[1]。随着现代计量经济学研究的发展,分位数回归估计引起了研究学者们的广泛关注,在传统的分位数回归进行估计的方法中,基于贝叶斯分析的方法比频率学派的方法更有优势,因此越来越多的学者更加关注基于贝叶斯的分位数回归估计的研究。Koenker等研究了分位数与非对称拉普拉斯分布(Asymmetric Laplace Distribution,ALD)之间的关系[2]。2001年,Yu等[3]基于文献[1]提出的ALD对贝叶斯分位数回归的参数进行估计,同时证明了即使先验分布是不适当的,得出的后验分布也是合适的,故可选无信息的先验分布;2009年,王新宇等指出ALD的尺度参数不应该假定为常数1[4]。何凤霞等对分位数回归在R软件中的应用领域方面做出了相关总结[5]。2015年肖北芳通过MCMC算法的M-H抽样模拟得到参数的后验分布,验证了金融发展与城乡差距的倒“U”关系在我国样本县域经济中存在统计显著[6]。霍翠伟在2018年基于贝叶斯分位数回归对因变量为连续和离散的情况下作了研究[7]。2019年,方丽婷等提出了空间滞后分位数回归模型的贝叶斯估计方法,该方法在小样本条件下具有良好的估计效果和稳健性[8]。同年,邸俊鹏等对基于贝叶斯估计方法的二元选择分位数回归模型进行研究,模拟实验结果表明,小样本下对二元选择分位数回归模型进行贝叶斯估计比频率学派方法的估计效果更佳,统计推断更准确[9]。Zhou等针对未知跳跃数的情况提出了一种使用局部多项式技术检测跳跃的新程序,通过模拟实验证明提出的方法在广泛的实际环境中表现良好[10];Xu等提出了一种贝叶斯非参数方法来同时估计非交叉的非线性分位数曲线,当数据稀疏时,该模型可以更好地恢复响应分布的分位数[11];张发赶等利用非对称拉普拉斯分布提出一种新的混合分位数回归模型,并基于所提出模型及算法对城市房价数据进行了分析[12];潘莹丽等在缺失数据的条件下对模型进行分位数回归[13];Liu等基于贝叶斯方法对离散响应的回归模型进行研究,同时证实了该方法得到的后验分布不仅与响应的真实分布无关,而且对于未知模型参数的不正确先验分布也是正确的[14]。

WinBUGS软件在1989年由英国剑桥的生物研究所编译,是一种以MCMC方法为基础的贝叶斯分析方法,将所有的未知参数看作随机变量,随之被相关研究学者引用到分位数回归的领域中,2018年,邸俊鹏等基于WinBUGS软件用泊松分布指定ALD的似然函数,并且验证了尺度参数应该被参数化,同时指出可用二项分布或负二项分布来指定ALD的似然函数[15]。基于此,本文采用二项分布指定ALD的似然函数,在WinBUGS软件中实现贝叶斯分位数回归估计的相关分析,当贝叶斯参数估计的后验分布的表达式复杂或难以表示时,采用Gibbs抽样算法可以得到后验分布相关的统计性质。

1 Gibbs抽样

在统计分析中,常用的计算方法有极大似然估计算法和贝叶斯算法。在现实应用中,由于后验分布一般都是非标准形式、复杂、高维的分布,因此采用贝叶斯算法中的马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)方法。在MCMC方法中,常用的2种算法是:Gibbs抽样和Metropolis-Hastings方法[17],Gibbs抽样是MCMC方法里最简单且应用最广泛的抽样方法,本文主要是基于Gibbs抽样对贝叶斯分位数回归的参数进行估计。

Gibbs抽样的具体步骤如下:

当T只含有一个元素时,称为单元素Gibbs抽样(single-site Gibbs sampler),单元素Gibbs抽样的具体步骤如下[16]:

第三步:令t=t+1,返回第二步,依此重复进行。

2 非对称拉普拉斯分布的贝叶斯参数估计

在基于ALD的贝叶斯分位数回归估计中,假定线性的随机误差项服从ALD,并且用二项分布指定ALD在WinBUGS软件中实现,得到参数后验分布的相关统计性质。

2.1 非对称拉普拉斯分布

2.2 线性模型

假定分位数回归线性模型为

令Z(x;β)=β0+β1x,则y=Z(x;β) +u,其中:因变量为y;自变量为x;待估参数为β0,β1;随机误差项u～ALD(μ,σ,q),即y～ALD(Z(x;β),σ,q)。

2.3 二项分布

记X为n重伯努利实验中成功(记为事件A)的次数,则X的可能取值为0,1,…,n,记p为每次实验中A发生的概率,即重伯努利实验的基本结果记作ω=(ω1,ω2,…,ωn)。若某个样本点则ω1,ω2,… ,ωn中有k个A,n-k个,由独立性可得,P(ω)=pk(1-p)n-k,而事件{X=k}中共有个这样的ω,故X的分布列为。1,…,n这个分布称作二项分布,记为X～b(n,p)[4]

2.4 二项分布指定的非对称拉普拉斯分布

在WinBUGS软件中,只包含了23种经常用的分布来指定先验分布的似然函数,然而对于泊松分布、二项分布和负二项分布等,则需要相关的一些编程技巧和数学的转换才能在WinBUGS软件中实现参数的估计。首先在WinBUGS软件中编译二项分布指定ALD的似然函数的程序;然后在Rstudio软件中用“bugs()”函数调用WinBUGS编译且已保存的程序,并基于WinBUGS软件进行Gibbs抽样,实现了贝叶斯分位数回归的模拟。

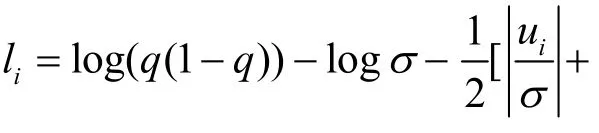
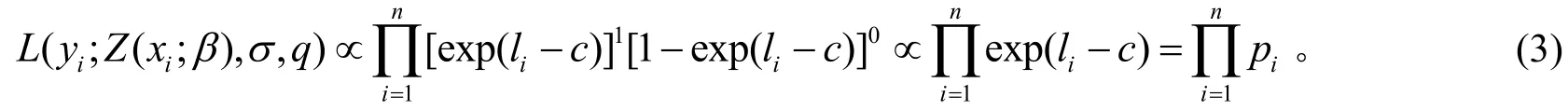
3 数值模拟

生成随机数据的模型为Y=1+ 2X+ε,其中X～U( 0,10),ε～ALD( 0 ,1,q)。利用生成的随机数据对模型(1)进行模拟。

3.1 尺度参数σ设定为1

当尺度参数σ设定为1,待估参数为β0和β1时,假定待估参数β0和β1的先验分布服从正态分布,由贝叶斯定理可知,参数的联合后验分布为其中,f()β为待估计系数β的先验分布,则数据的对数密度函数可表示为

将式(4)代入式(2),可得参数pi的表达式

将式(5)代入式(3),故参数的联合后验分布可表示为

用二项分布指定的ALD,当迭代10 000次,预烧期为5 000次时对参数的联合后验分布进行Gibbs抽样得到的轨迹图和自相关图更加平稳;在相同的迭代次数和预烧期不同的先验分布、分位点及样本容量下参数β0和β1的5 000个抽样值的轨迹图均在设定值上下波动,自相关系数随着滞后期的增加而逐渐趋于零,故马尔科夫链收敛。限于篇幅,仅展示当参数先验分布设定为β～N(0,100),在0.75分位点下且样本容量n为75时,参数β0和β1的5 000个抽样值的轨迹图、密度图以及自相关图,结果显示参数β0和β1的5 000个抽样值的轨迹图均在设定值上下波动,密度图的宽带足够小,且自相关系数随着滞后期的增加而逐渐趋于零,如图1所示。

图1(a) β0抽样值的轨迹图、密度图及自相关图

图1(b) β1抽样值的轨迹图、密度图及自相关图

如表1所示,对分位数回归的线性模型参数进行Gibbs抽样,迭代次数为10 000次,预烧期为5 000次,可得到参数后验分布的均值、标准差和模拟误差等。

表1 σ设定为1时参数β0和β1的均值、标准差及MC误差

续表1

由表1可知:(1)当先验分布和分位点相同时,随着样本容量n的增大,待估参数β0和β1的标准差和MC误差逐渐变小;(2)当先验信息、样本容量n以及分位点相同时,β1的标准差和MC误差总是小于β0的标准差和MC误差,即在WinBUGS软件中得到的系数项的估计精度往往高于常数项的估计精度;(3)在样本容量和分位点相同条件下,随着先验分布的增强,参数β0和β1的标准差和MC误差变小,即增强先验信息时可提高参数的估计精度;(4)在这3种先验设定中,当样本容量和先验信息相同时,除了先验信息为β～N(0,100),样本量为100,参数β0和β1在0.25分位点下的标准差和MC误差比在0.5分位点、0.75分位点下的标准差和MC误差更小,其他条件下,参数β0和β1在0.25分位点下的标准差和MC误差均比在0.5分位点、0.75分位点下的标准差和MC误差更大,即参数β0和β1在中位数和高分位数的估计精度较高。

3.2 尺度参数σ参数化

ALD中的尺度参数设定为1时,尽管参数的估计精度较高,但在实际应用中是不恰当的,因此,应当对ALD中的尺度参数进行参数化[4]。

当参数σ,β0和β1均待估计时,设定σ的初始值为1,假设待估参数β0和β1的先验分布为正态分布和尺度参数σ的先验分布为卡方分布,当尺度参数σ的卡方分布自由度为4时,3个待估参数的平稳度更高,由贝叶斯定理可知,参数的联合后验分布为其中,f(β)为待估计系数β的先验分布,g(σ)为尺度参数σ的先验分布,且σ～χ2(4),则数据的对数密度函数为

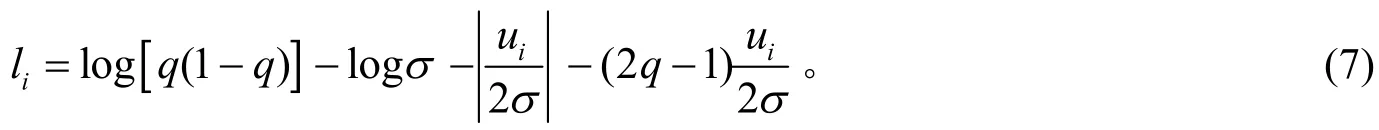
将式(7)代入式(2),可得参数pi的表达式

将式(8)代入式(3),可得参数的联合后验分布的表达式

图2为二项分布指定ALD的似然函数,当迭代10 000次,预烧期为5 000次时对参数的联合后验分布进行Gibbs抽样得到的轨迹图和自相关图更加平稳;在相同的迭代次数和预烧期不同的先验分布、分位点及样本容量下参数β0、β1和σ的5 000个抽样值的轨迹图均在设定值上下波动,自相关系数随着滞后期的增加而逐渐趋于零,因此抽样构成的马尔科夫链均收敛。限于篇幅,仅展示当参数先验分布设定为β～N(0,100),在0.75分位点下且样本容量n为75时,参数β0、β1和σ的5 000个抽样值的轨迹图、密度图以及自相关图,结果显示参数β0、β1和σ的5 000个抽样值的轨迹图均在设定值上下波动,密度图的宽带足够小,且自相关系数随着滞后期的增加而逐渐趋于零。

图2(a) β0抽样值的轨迹图、密度图及自相关图

图2(b) β1抽样值的轨迹图、密度图及自相关图

图2(c) σ抽样值的轨迹图、密度图及自相关图

如表2所示,对分位数回归的线性模型参数进行Gibbs抽样,迭代次数为10 000次,预烧期为5 000次,可得到参数后验分布的均值、标准差和模拟误差等,由表2可知:(1)当先验分布和分位点相同时,随着样本容量n的增大,参数β0、β1和σ的标准差和MC误差逐渐变小;(2)在先验信息、样本量以及分位点相同条件下,标准差的大小为β1＜σ＜β0,而MC误差的大小为σ＜β1＜β0;(3)在样本容量和分位点相同条件下,随着先验分布的增强,参数β0、β1和σ的标准差和MC误差变小,即增强先验信息时,可提高参数的估计精度;(4)当先验信息相同且样本量为100时,参数β0、β1和σ在0.75分位点下的标准差和MC误差比在0.25分位点、0.5分位点下的标准差和MC误差更小。

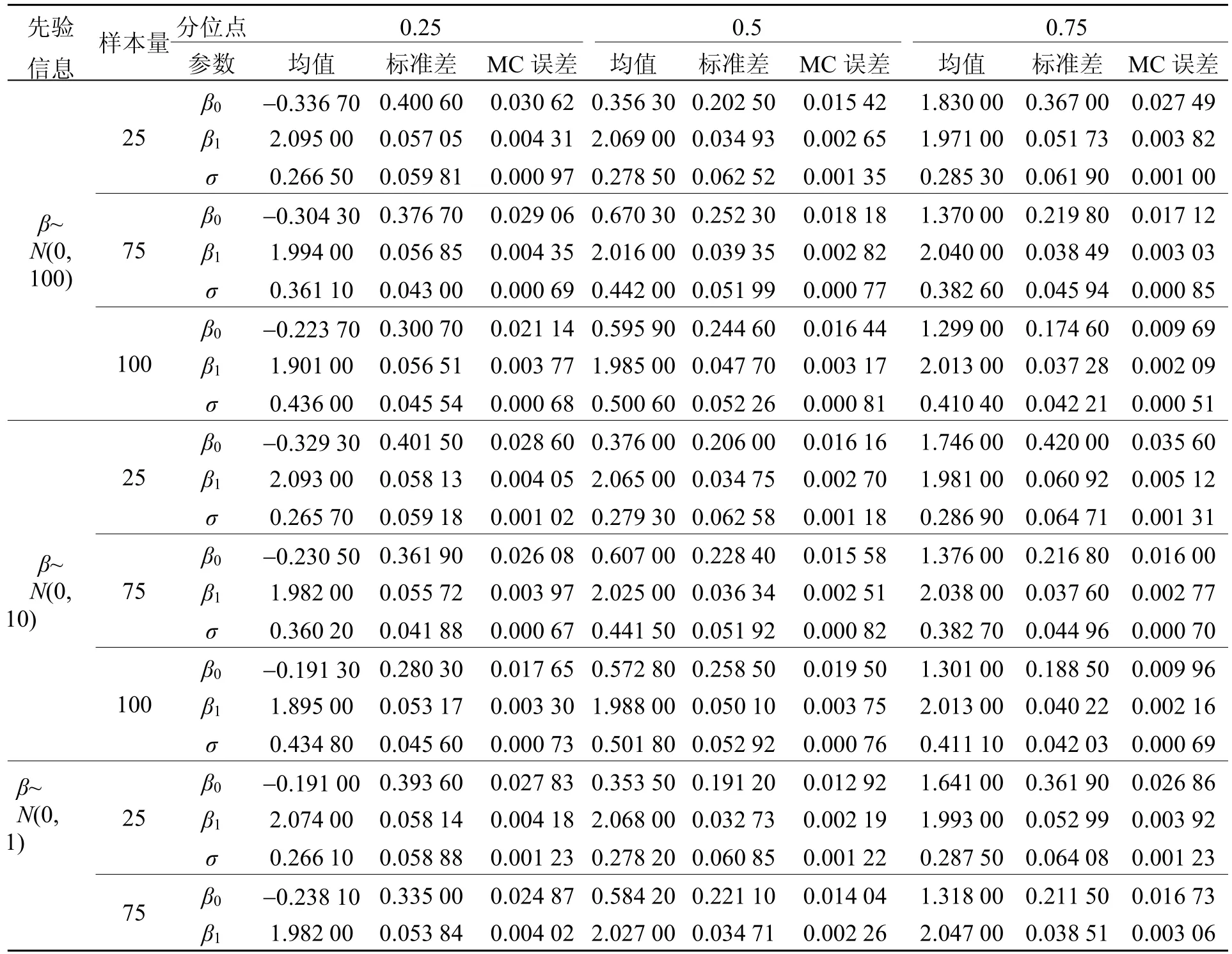
表2 参数σ,β0和β1均待估时的均值、标准差及MC误差

续表2

对比表1和表2可知,当先验信息、样本量、参数与分位点相同时,表2中参数β0和β1的标准差与MC误差均小于表1中参数β0和β1的标准差与MC误差。因此,对尺度参数σ进行参数化可以提高参数β0和β1的估计精度,即尺度参数σ应参数化,而不是设定为1。

用二项分布指定ALD的实验结果与邸俊鹏用泊松分布指定ALD的似然函数[15]的实验结果相比,尺度参数进行参数化后,2种实验的参数统计量性质效果一样好。

综上所述,当尺度参数未参数化时,利用二项分布和用泊松分布指定ALD的似然函数得到的参数统计量性质效果一样;尽管先验分布不适当,但是得到的后验分布也是适当的。

4 结束语

本文利用二项分布指定ALD的似然函数,通过对分位数回归线性模型进行Gibbs抽样得到参数后验分布的相关统计性质,通过模拟实验证实了尺度参数被参数化得到参数后验分布的估计量统计性质比尺度参数假定为1时的估计效果更好且更稳健;同时也证实了适当的先验分布可以提高待估参数的估计精度。接下来可考虑用负二项分布指定ALD的似然函数,分析所得结果是否与此方法一样理想或比此方法更好。