六腿式移动机械手基座安装位置的优化研究
2022-05-06张江锋吴志光
张江锋,吴志光
(池州职业技术学院 机电与汽车系,安徽 池州,247100)
腿式移动机械手(LMM)是一种将串行机械手刚性安装在多腿移动平台上执行特定任务的组合机器人系统。LMM可以在不平坦的地形上行走,甚至可以在不改变腿尖接触地面的情况下调整姿态。这使得LMM可以在复杂环境执行数据采集、探测等工作任务,比如钱进等[1]研制的水下多腿滑翔机器人、王雅雪等[2]设计的六腿行走机器人和吴晓[3]研究的腿球机器人等等。在LMM机器人系统中,多腿平台提供了机动性,而操作任务则由机械手完成。这两者的集成是非常重要的,在多腿平台上,由于机械手基座的位置会影响其工作空间、可操作性、稳定性等,因此需要仔细选择机械手基座的位置,对机械手基座的安装位置需要重点考虑。
Rehman等[4]、Murphy等[5]和Abe等[6]只考虑工作空间作为决定基座位置的衡量标准,将串行机械手的基座位置选择在四腿机器人的中间靠前位置。但是,这种情况下前腿上的载荷高于其他腿上的载荷,并且腿间的接触力分布非常不均匀,这会导致稳定性受损。Ackerman[7]将机械手置于平台的顶部,位于四腿机器人的前腿之间。Adachi等[8]更倾向于四腿机器人顶部的中点。然而,Ackerman和Adachi等没有讨论选择这些位置的原因。Gardner和Venlinsky[9]只考虑可操作性参数进行数值分析,对机械手在移动机器人上的最佳位置进行研究。总之,对于机械手基座的安装位置而言,机械手的工作空间、可操作性以及组合机器人系统的稳定性都是非常重要的研究内容,需要综合考虑这3个方面的耦合效应。目前还没有关于六腿平台上机械手最优位置选择问题的研究,因此,本文的研究对象为六腿式移动机械手。
机械手与多腿平台的结合提高了机械手在给定位置的工作空间,比固定基座串联机械手的工作空间大。然而,多腿机器人串联机械手的工作空间难以进行解析求解确定。Bhavanibhatla和Pratihar[10]试图对安装在六腿平台上的串行机械手的工作空间进行可视化,但没有提供任何封闭形式的方程。本文要面对的首要挑战是量化组合机器人系统(即机械手和六腿平台)的工作空间,将其作为机械手基座在多腿移动平台上定位的决定参数之一。
从运动学的角度来看,可操作性是定量估计机械手能够轻松改变其位置和方向的参数[11]。可操作性的代表性度量之一是可操作性度量。这个度量可以用机器人系统的雅可比矩阵来计算。本文导出的腿式移动机械手的位姿约束到达矩阵与文献[12]中的类似。因此,本文采用了螺旋理论。
为了保持多腿车辆的稳定性,机器人的重心必须始终保持在支撑腿形成的凸多边形内,以防止机器人系统翻倒。Agheli和Nestinger[13]等提出了5个不同的标准来确定机器人系统的稳定性。这些准则包括:基于距离的准则、基于角度的准则、基于能量的准则、基于矩的准则和基于力的准则。对于多腿机器人而言,接触通常发生在腿尖和地面之间。本文采用了基于力的准则,考虑将作用于机器人和地面接触点之间的法向反作用力,即腿部受力,作为衡量稳定性的参数。
本研究为了寻找机械手在六腿机器人平台上的最佳安装位置,考虑了腿式移动机械手的工作空间、可操作性度量和机器人腿部力分布这3个性能参数,对1个实际的六腿式移动机械手进行数值分析。利用机器人操作系统(ROS)生成的机器人系统碰撞感知可达性图进行工作空间分析。采用螺旋理论推导末端执行器的扭转速度坐标与组合机器人系统的关节构型向量之间的关系[14]。本文中使用的LMM的运动学模型公式类似于文献[12]中的推导。通过基于腿力稳定裕度的稳定性参数来评估腿部受力在腿之间的分布。对于机械手在六腿平台上不同安装位置的情况,计算了上述3个性能参数。最后,通过数值分析确定了机械手在六腿平台上的最优安装位置。
1 腿式移动机械手描述
本节描述了所研究的LMM机器人系统(即机械手和六腿移动平台)和相关参考系,机器人系统如图1所示。机器人系统有6条腿,1个机械手安装在平台上。六腿平台的每条腿和机械手各有3个连杆。移动平台的质量为895 g,机械手的质量为443 g。机器人系统的运动尺寸如下:平台面积 =415 mm×161 mm,腿链_1的长度 =83.5 mm,腿链_2的长度 =120 mm,腿链_3的长度 =98 mm,机械手链_1的长度 =39 mm,机械手链_2的长度 =380 mm,机械手链_3的长度 =285 mm,夹持器长度为72 mm。

图1 腿式移动机械手
参考系的分布如图2所示。全局(固定)参考坐标系用G表示,体坐标系B附在主体平台上。坐标系Si连着一条腿臀根部,第i条腿与主体相连,相对于体坐标系B保持固定。Fi表示刚性固定在第i条腿脚上的腿坐标系,其原点附着在与地面的接触点上。接触参考系Ci固定在地面的第j条腿与地面接触点。机械手的基座连接坐标系和末端执行器坐标系分别用bo和ε表示。

图2 坐标系分布
为了进行数值分析,做了以下假设:所有的六条腿都要与地面接触(站立阶段);机械手将只安装在平台的顶部;设计的主体是对称的,使所有的6条腿均匀地放置在平台的两侧。
2 站立及关节运动学
本节介绍了机械手末端执行器运动与组合机器人系统协调关节运动之间的运动关系。假设多腿平台的腿始终与地面接触,LMM机器人系统的运动学关系适用于准静态姿态和到达阶段(reach phase)。这个运动学模型的更多细节可以参考文献[12]。机械手末端执行器与组合体(机械手与多腿平台)关节运动的运动学关系为:

JR是位姿约束的Reach雅可比矩阵,可以表示为:
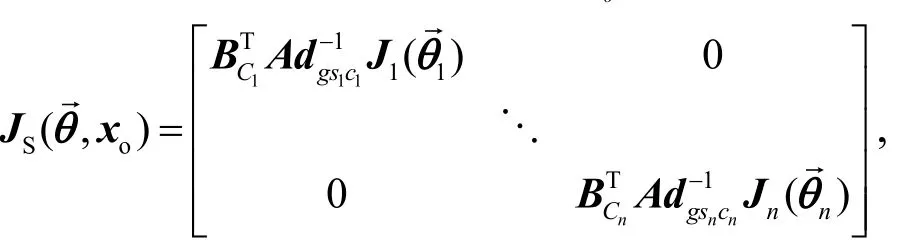
其中,J1,J2,…,Jn是n条腿的雅可比矩阵,Jm是机械手的雅可比矩阵。是n条腿的关节角度向量,是机械手的关节角度向量。xo表示体坐标系相对于全局坐标系的位置向量。Θ表示组合机器人系统(所有腿和机械手)的关节角度向量,可写成表示第i个脚处的力螺旋基,其中表示与g(齐次坐标变换矩阵)相关联的伴随矩阵变换,它将扭转坐标从一个坐标系变换到另一个坐标系,表达式为[14]:表示某个坐标系b在坐标系a中的旋转矩阵,是某个坐标系b的位置向量在坐标系a中的斜对称矩阵。表示机械手末端执行器速度在全局参考系(G)下的扭转坐标。

重写式(1),可得,
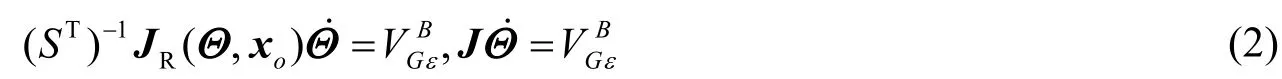
3 研究方法
本节详细讨论了数值分析所需的所有参数概念,即工作空间、可操作性度量和基于腿力的稳定裕度(FFSM)。
3.1 工作空间
串行机械手的工作空间是指其末端执行器所能覆盖的空间体积。考虑腿式平台处于定姿状态,对六腿机器人平台上不同基座位置的串联机械手进行了工作空间分析。自碰撞限制了机械手的运动,从而限制了机器人的工作空间。在平台上不同的安装位置,机械手会有不同的关节角度限制,以避免与自身和平台体碰撞,因此会有不同的工作空间。
工作空间分析有两个主要挑战。首先,在考虑自身和六腿平台碰撞的情况下,生成串行机械手的工作空间。第二个挑战是量化工作空间。为了解决这一问题,利用Reuleaux库生成了考虑自碰撞的机器人系统可达性图。Reuleaux库[15]是一个开源库,可以用于机器人可达性分析。Reuleaux可达性图生成器使用颜色代码创建可达性图,如图3所示。可达性图是机器人末端执行器所能达到的所有姿态,由一组不同颜色的球体表示。每个球体表示机器人工作空间中的一个点,该点至少有一个逆运动学解。颜色代码:蓝、绿、黄、红,按照上述顺序给出了逆运动学解数量的递减顺序。
生成可达性图所需的2个主要参数是半径和分辨率。半径参数指定要用于可达性图生成的操纵器底座周围区域的最大半径。分辨率参数表示球体的直径,或者2个相邻球体中心之间的距离。在整个工作空间分析中,半径和分辨率参数保持不变。半径设置为1 m,分辨率设置为0.05 m。
为了生成可达性图,Reuleaux库将机器人周围的空间离散化,并对可达姿态进行采样。可达性映射中可达球体的总数对于不同的机械手位置是不同的,因为它取决于工作空间的体积。因此,由图3可知,可达球体数量是每个机械手位置工作空间体积的量化度量。可达性度量也是比较工作空间的一个很好的参数。在这种情况下,需要对每个可达球体计算一个可达性度量,然后将所有可达性度量的总和作为工作空间比较的量化度量。在本研究中,考虑了工作空间的体积,因此,可达性图中的球体数量作为工作空间比较的量化度量。
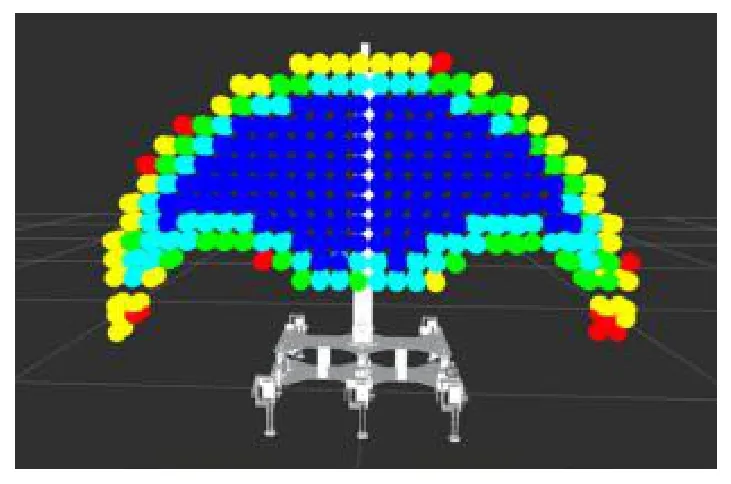
图3 可达性地图的半切割视图
3.2 可操作性及其度量

3.3 腿端受力分布
本文使用基于腿力的稳定裕度(FFSM)评判稳定性,因为它明确地依赖于从地面接触支持的正常反作用力。因此,FFSM可以直接采用地面作用在腿尖上的法向反力进行计算[13]:
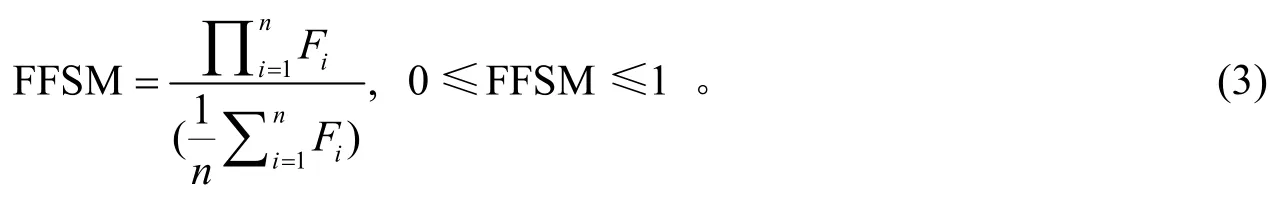
其中Fi为作用于第i条腿尖端的法向反作用力,n为与地面接触的腿数。在给定的时间点,腿尖上的反作用力的值应该总是大于或等于0。它不可能是负的,因为腿不能抓住地板。当腿与地面失去接触时,法向反作用力的值等于0。
FFSM度量的值在0和1之间变化,其中0表示作用于其中一个腿尖(至少)的法向反力等于0,而1表示力在所有腿中平均分布。当力平均地分布在所有的腿上时,系统处于高度稳定的状态,这是所期望的。因此,当FFSM值接近于0时,腿力分布的变化非常大。另一方面,FFSM值接近1,说明腿力分布的变化较小。
图4展示了FFSM参数的变化情况。然而,这里只考虑2个力:F1和F2(式(3)中i从1到2变化),为了可视化FFSM相对于法向反作用力(Fi)的变化。两个力的变化范围从0~5 N。由图4可知,当两个力相等时,FFSM等于1。另一方面,当其中一个力为0时,FFSM等于0。然而,两个力都等于0,在实际情况中是不可能发生的,因为当机器人在地面上移动时,至少有一条腿与地面接触。
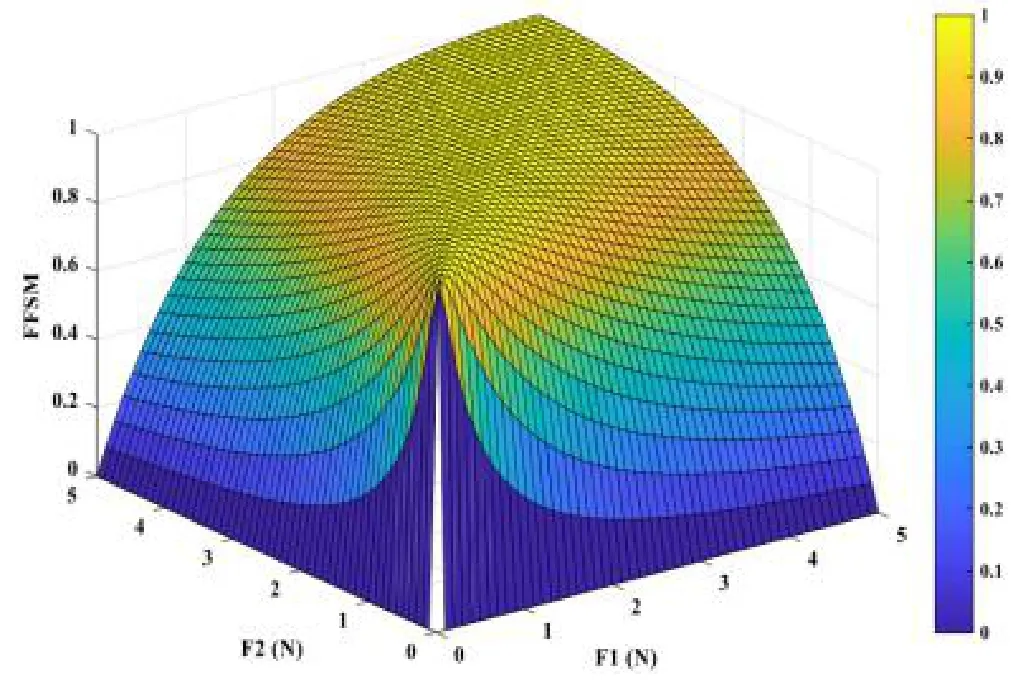
图4 两种力情况下FFSM参数的变化
利用虚拟机器人仿真得到腿部受力,在Solidworks上进行运动分析。在本文的工作中,考虑了六腿机器人的姿态和机械手的固定构型与关节角θ1=0,θ2=0和θ3=π/2,末端执行器上的有效载荷是200 g(见图5)。将机械手放置在不同的位置,其配置不发生变化,通过仿真得到机器人腿上的法向反作用力。然后,利用这些力,用式(3)计算相应的FFSM值。

图5 力分析时的LMM配置
4 结果和讨论
在进行分析时,通过对六腿机器人顶面进行对称划分,充分发挥了六腿机器人平台的对称性优势。这减少了分析中要考虑的机械手底座位置的数量。本研究所考虑的六腿平台在水平面上的纵轴和横轴是对称的(见图6)。因此,通过纵轴和横轴将六腿平台分为4个对称部分。在平台上预先选择不同的机械手底座位置,如下所述。
在四分之一的平台中,有44个机械手底座位置,xm从0~30 mm,间隔10 mm,ym从0~200 mm,间隔20 mm(见图6)。在每个位置,将机械手底座改变到相应的点后,计算工作空间、可操作性度量和腿部力分布3个参数。由于这3个参数都是机械手在六腿平台上基座位置的函数,因此对于不同的预定义位置,3个参数的值会不同。

图6 六脚平台的俯视图
为了进行工作空间分析,按照3.1节中提到的步骤生成每个机械手底座位置的可达性图。在(xm=0,ym=0)和(xm=30,ym=200)2个不同位置获得的机械手可达性图如图7所示。利用该方法,将可达性映射中的球数作为工作空间的量化度量。

图7 工作空间表示
b处(所得球数为5 096)的工作空间大于a处(所得球数为4 712)的工作空间。各点工作空间的变化如图8所示。可以观察到,由于考虑自碰撞时允许更多的关节运动,与六腿机器人的中点(xm=0,ym=0)相比,角点的工作空间更大。换句话说,当机械手的末端执行器位于平台的中点时,由于自身碰撞,其可达性受到限制。在不同的机械手基座位置下,可操作性测量值会发生变化,如图9所示。由图9可知,可操作性测度值在xm和ym方向上均由平台中心向边缘递增。
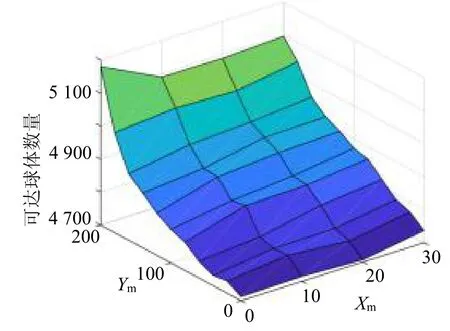
图8 工作空间的变化

图9 可操纵性参数变化
最后,计算了所有44个机械手底座位置的腿部力分布。得到的腿力分布变化如图10所示。在中点(xm=0,ym=0),腿部受力在两腿间的分布几乎相等,因此FFSM值趋于1。在正xm和正ym方向上,FFSM值逐渐减小,表明腿部受力在腿间分布的不均匀性在增加。
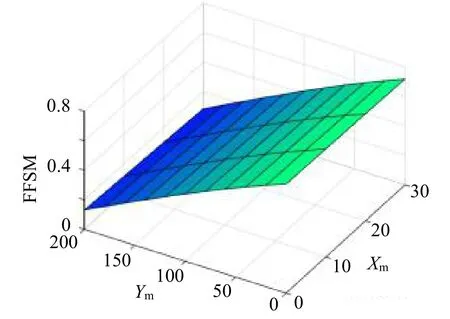
图10 FFSM参数变化
工作空间和可操作性度量的参数值在正向xm和ym方向上都在增加。另一方面,FFSM值在正向xm和正向ym方向上都呈下降趋势。如果选择(xm=0,ym=0)作为机械手基座位置,则脚反力在两腿之间的分布是相等的,但工作空间和可操作性较低。另一方面,在(xm=0,ym=200)或(xm=30,ym=200),工作空间和可操作性会很高,但腿部受力在两腿间的分布会非常不均匀,前腿将不得不承担更多的负载,这样稳定性较差。因此,需要选择一个最优的机械手基座位置,使其中3个参数都有比较有利的值。

为了便于比较,对每个参数的采样数据采用Pnorm=p/{max(p)-min(p)}的表达式进行归一化。图11为六腿平台上机械手底座全部44个位置3个参数的比较。最优的位置应该使由式(4)给出的3个参数之间的差的平方和最小,式(4)中Ns为可达球数,mm为归一化尺度下的可操作性度量。

图11 3个参数的比较
图12展示了式(4)的计算结果。从图12的分析中可以发现,在(xm=30,ym=100)处的机械手底座位置是最优的,其平方和的差异在标准化尺度上是最小的。
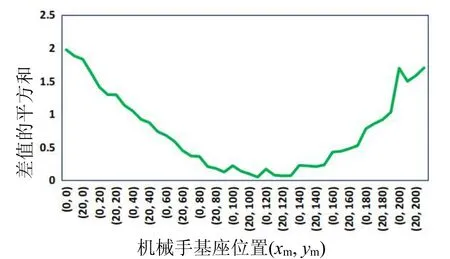
图12 3个参数之间的差的平方和
此外,需要注意的是,如果相对于工作空间和可操作性而言,稳定性(FFSM量化)得到了更多的权重,那么可选择位于纵轴上的点(xm=0,ym=100)作为最佳位置,位于与前腿和中腿等距的位置。在固定ym=100 mm,xm变化范围为0~30 mm时,3个参数的结果如图13所示。由图13可知,在xm=0 mm处的腿力分布优于xm=30 mm处的腿力分布。

图13 xm从0到30 mm变化时3个参数的比较
5 结论
本文选取工作空间、可操作性度量和腿力分布作为性能参数,并在平台不同安装位置计算这些参数,最后给出了计算结果,并利用这些参数的综合效应来确定最佳安装位置。
研究结果表明:(1)在六腿平台的顶面上,从中点到纵轴和横轴的边缘,其FFSM值逐渐减小,而工作空间和操纵性度量值则逐渐增大;(2)在上述3个性能参数同等重要的情况下,对称六腿平台上机械手的最佳安装位置位于前、中腿之间,且远离纵轴,最佳位置为(xm,ym)=(30 mm,100 mm);(3)如果为了有更好的稳定性,腿部力比工作空间和可操作性占更多权重,那么最佳的位置将是在前腿和中腿之间,位于纵轴上,最佳安装位置为(xm,ym)=(0 mm,100 mm)。
