在数学实验中理解“余数”——《有余数的除法》教学片断与思考

文|张 彦

《有余数的除法》是苏教版教材二年级下册的教学内容。作为这个单元的起始课，本课教学的重点是认识“有余数的除法”，难点是理解“余数要比除数小”。在教学中，教师的目光不能仅仅停留在课时的知识点上，而是要具备知识、方法和过程的结构意识，进行整体架构。对于二年级的学生，对“有余数的除法”的知识建构和意义理解感到比较抽象深奥，基于这样的学情，怎样促进学生理性思维发展呢？数学实验是打开学习的有效方式，让学生通过动手动脑，“做”中学，在问题启思下，借助实验材料，展开操作和交流，从而认识有余数的除法，理解余数和除数之间的关系。

片断一：在“分苹果”的数学实验中完善建构

师：同学们，认识它吗？（小猪佩奇）

师：小猪佩奇正在果园里摘苹果。摘了10个苹果（出示10个苹果图），每人分2个，可以分给几人呢？

生：5人。

师：每人分2个，也就是2个2个分，可以分给5人，正好分完。佩奇把结果记了下来。

师：那10个苹果，如果每人分3个，结果会怎样？每人分4个？5个呢？动手分一分、填一填、说一说。

师：我们可以像佩奇那样，同桌合作，用圆片代替苹果分一分，把每次分的结果记在表格里。再互相说一说，每次分得的结果怎样？

交流：老师收到了这些分法，看得懂吗？你们也是这样分的吗？谁来介绍一下？结合图说一说。

生1：10个苹果，每人分3个，可以分给3人，还剩1个。

生2：10个苹果，每人分4个，可以分给2人，还剩2个。

生3：10个苹果，每人分5个，可以分给2人。

出示《记录单》：

?

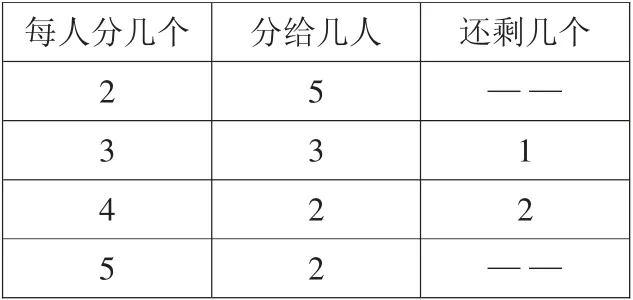
师：把10个苹果平均分，我们得到了这些结果。仔细观察，你有什么发现呢？同桌讨论。

生：有的正好分完，有的有剩余。

师：（追问）哪些情况是正好分完的？有剩余的呢？

发现：把10个苹果平均分，会出现两种情况：正好分完、有剩余。

【思考：数学实验不是简单的动手操作，而是促进学生对未知探索、主动思考和发现的一种方式，学生的已有经验是“10个苹果，每人分2个，可以分给5人，正好分完”，那每人分3个、4个呢？这就产生了认知冲突，在结果不可知的情况下，教师组织学生用数学实验的方式去探究发现，体现了实验设计的必要性与合理性，通过有序地分一分，记录分的结果，根据过程体验和数据观察，较好地感受平均分有两种情况，“正好分完”和“有剩余”，帮助学生形成更加完整的知识体系架构。】

片断二：在“除法算式”表征中渗透数形结合思想

师：像这样正好分完，你会用除法算式表示吗？

生：10÷2=5（个）。

师：这一种有剩余的情况，也可以写一个除法算式吗？

生：10个苹果，每人分3个，可以分给3人，10÷3=3（人）。

师：还剩1个可以怎样表示呢？可以在后面点上6个小圆点（……），再在小圆点（……）后写1（个）。

师：会读吗？

生：10除以3等于3人还剩下1个。

师：剩下1个就是“余1个”。

师：这个算式表示什么意思？谁能完整地说一说？

生：10个苹果，每人分3个，可以分给3人，还剩1个。

师：两个“3”，意思相同吗？分别表示什么？1呢？

介绍：1表示剩下的个数，不够再分，在除法中，它就叫“余数”。这就是有余数的除法。

师：今天这节课我们就来认识《有余数的除法》（揭示课题）。

师：10个苹果，每人分4个，也可以用有余数的除法算式来表示吗？

生：10÷4=2（人）……2（个）。

师：两个2表示的意思相同吗？

生：商2表示可以分给2人，余数2表示剩下2个苹果。

【思考：引导学生对操作结果加以提炼，进行数学表达。10个苹果，每人分3个，可以分给3人，还剩1个。从图形表征到算式表征，提出有余数的除法算式，展开读写认知，结合平均分的过程与结果，在抽象的算式与直观的操作之间建立联系，沟通有余数除法算式的算理，理解其含义，这样的教学活动更利于学生形成初次的有余数除法的算式表达，建立有余数除法的算式模型。】

片断三：在“摆小棒”的数学实验中探究余数与除数的关系

1.动手做：“用12、13、14根小棒摆正方形”。

师：佩奇分完了苹果，又在做什么了？他在摆小棒！

佩奇：我用4根小棒摆1个正方形，8根小棒摆2个正方形。像这样用12、13、14根小棒摆正方形，结果会怎样呢？

师：你们会和佩奇一起来探究这个问题吗？我们来动手做一做。

师：同桌合作，先用小棒摆一摆，根据结果写算式，填在表格里，完成后，同桌互相交流你们的想法。

教师巡视，了解学生用小棒摆正方形的过程和结果。

师：这些摆法你都看得懂吗？都对吗？谁来给大家完整地介绍一下？

学生介绍摆法和记录情况（如图）。

师：你们也是这样摆的吗？

师：这些商表示什么？余数呢？

生：商表示正方形的个数，余数表示剩下的小棒根数。

2.静心想：用“15、16根小棒摆正方形”。

师：观察以上这些算式，你有什么发现吗？如果用15根小棒摆正方形结果会怎样？用16根小棒呢？

挑战：你能不用小棒，直接想一想，写出算式吗？在《作业单》上试一试。

教师巡视，收集学生资源。

师：老师收集了两份作业，比较一下，有什么相同和不同？

生：15除以4的算式和结果是相同的，16除以4的结果不同。

师：（圈出15的两个算式）没有摆小棒，是怎么想到15根可以摆成3个正方形，还剩3根的呢？

生：可以根据14根来想，因为15根比14根多1根，14根可以摆3个正方形，余2根，那么15根就还是可以摆3个正方形，余3根。

师：你真有办法，不用小棒，根据14根就能直接推想出15根的结果。

师：是啊！15比14多1根，可以摆3个正方形，还剩3根。算式是：15÷4=3（个）……3（根）。

师：（圈出16的两个算式）关于16根，两个算式结果不一样，你们赞同谁的呢？为什么？

生1：余数不能是4。因为只要满4根就可以摆成一个正方形。

生2：剩下的只能是不够摆的，不满4根的，也就是余数要比4小，不能是4。

生3：在这里，剩下的根数只会是1、2、3根，不会是4根。

师：把这4根再摆成一个正方形，所以，商3变成了4，现在的余数是几？（0）余数是0，可以省略不写。

形成算式：16÷4=4（个）。

3.揭示余数和除数的关系。

师：小棒根数在变，余数也在变，这里的余数大小有什么秘密呢？同桌互相说一说。

感悟：余数可能是1、2、3，不能是4，余数比4小。

师：在除法算式中，余数和除数有怎样的关系呢？

生：余数都比除数小。

师：如果继续摆，17÷4，余数是几呢？18÷4？19÷4？20÷4呢？

学生再次感悟余数比除数小。

【思考：引导学生理解“余数要比除数小”，这是本课难点。教师仍采用数学实验的方式推进教学，在积累学生操作经验的同时更要激活思维、促进表达、深化认识，从而突破难点。基于以上思考，把例2摆小棒的活动切割成“动手做”和“精心想”两块，按照第一次实验的展开方式进行，同桌合作摆一摆，记录数据结果，数学算式表达。“用15、16根小棒摆正方形，结果又怎样？这一次你能不用小棒，直接想一想，写出算式吗？”这里的想不是毫无依据地想，是基于动手做经验的推想，因为15根比14根多1根，所以就比14根多剩余1根，由此推理出余数是3。用16根摆正方形的结果呢？仍然借助操作经验继续推想，但学生的想法出现了矛盾冲突，为什么余数不能是4呢？这是一个突破教学难点的重要问题，组织学生展开充分思辨，发现满4根又可以摆成一个正方形，那么余数只可能是哪些数？继而发现余数与除数之间的关系。从实验操作到理性推想，动静有机结合，学生的成功动机得到瞬时激发，知识难点得到有效突破，思维走向更深处。】

片断四：在数学游戏中再次感悟余数与除数的关系

师：做游戏的时间到了，同学们喜欢吹泡泡吗？泡泡很神奇，藏在了大屏幕里，让我来吹一吹。你们也想试一试吗？

师：数一数，吹出了6个泡泡，每次拍3个，几次拍完？

生：2次。

师：吹出了8个泡泡，每次拍3个，有剩余吗？剩几个？

生：剩2个。

师：还想吹吗？为了吹出更多的泡泡，我建议大家做一次深呼吸，泡泡多得数不清，但还是每次拍3个，如果最后有剩余，可能会剩几个？

师：你们是怎样想的？能用今天学到的知识告诉大家吗？

生：可能剩1个或者2个，一定比3小，因为在除法算式中，余数都比除数小。

【思考：数学游戏的设计是对“余数比除数小”知识的再一次感知和应用，吹泡泡的活动环节，从趣味角度看，学生参与主动性强，从思维角度看，深刻而且敏捷，紧扣难点，在游戏互动中进一步加深理解余数的意义，实现知识的建模。

两次数学实验的设计，完善了学生对平均分的认知建构，认识了余数，并理解了余数与除数的关系，实现了知识的建模过程，内容整体推进，活动有序进行。实验方式的展开，有利于学生把数与形很好地结合起来，把操作和思维自然地融合起来，把演绎和归纳合理地运用起来，数学实验是边做边想的过程，让思维在困顿处慢一点，在争鸣处清一点，在生长处活一点，数学实验的学习方式打开了学生的思维活动轨迹，教育的魅力因此得以彰显。】