求解病态线性方程组的精细积分新主元加权迭代法
2022-05-06王慧蓉常金勇
郝 强,王慧蓉,常金勇
(1.长治学院 数学系, 山西 长治 046011;2.西安建筑科技大学 信息与控制工程学院, 陕西 西安 710055)
对一般的线性方程组求解算法的研究已经非常成熟.但在许多实际问题中,往往会涉及病态方程组的求解问题.许多学者对病态方程组的求解算法进行了大量的研究.富明慧等[1]利用精细积分法的思想,将病态代数方程组归结为一个常微分方程初值问题的极限形式,提出了一种求解病态代数方程的精细积分解法,具有较高的精度和效率.唐丽等[2]通过在系数矩阵主元上叠加一个权值降低条件数,提出了求解病态方程组的主元加权迭代解法.潘轶等[3]将误差转移与主元加权迭代法相结合,提出了一种改进的主元加权迭代算法.富明慧等[4-5]将范数均衡法与精细积分法相结合,提出了一种范数均衡预处理精细积分法,以及一个求解病态方程组的形式简单、便于应用的迭代终止准则.
论文将新主元加权迭代法与精细积分法相结合,提出了一种求解病态线性方程组的精细积分新主元加权迭代算法,并用这种方法求解两种病态方程组.实验结果表明,论文提出的算法不仅提高了病态方程组的求解精度,而且大大减少了迭代次数,提高了计算效率.
1 精细积分法
对于线性方程组
Ax=b,
(1)
其中:系数矩阵A为正定矩阵.
对式(1)用预处理精细积分法进行求解.由
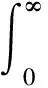
(-A)-1(0-1)=A-1,

记
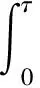
(2)
则

即
F(2τ)=(I+exp(-Aτ))F(τ),
(3)
式(3)两边同时乘以b,得
F(2τ)*b=(I+exp(-Aτ))F(τ)*b,
(4)
将式(4)写成迭代格式,得
xk+1=(I+exp(-2kAτ))xk.
(5)
对式(5)中的exp(-2kAτ)可以用精细积分求解.对exp(-Aτ)进行Taylor展开,取τ是一个非常小的正数,只需取前几项就能满足精度要求,得
(6)
将式(6)带入式(2),得
(7)
记
将(6)式写成等号,得
exp(-Aτ)=I+Ta.
由于
exp(-2kAτ)=(exp(-Aτ))2k=((exp(-Aτ))2)2k-1,
(exp(-Aτ))2=(I+Ta)2=I+2Ta+Ta2,
构造迭代格式
Ta=2Ta+Ta2,
(8)
循环k次后,有
exp(-2kAτ)=I+Ta,
(9)
将式(5)与式(8),(9)两个过程合二为一,写成迭代格式,即
(10)
2 精细积分新主元加权迭代法
根据主元加权的思想[6],对病态线性方程组(1),两边同时加上ωPx(ω>0,P为对角矩阵),其中
则病态线性方程组(1)变为
(A+ωP)x=b+ωPx,
(11)
将式(11)写成迭代格式为
(A+ωP)x(k+1)=b+ωPx(k).
(12)
定理1若A为正定矩阵,对于初始值x(0)=0,当0<ω<1时,由迭代格式(12)产生的序列{x(k)}收敛.
证明A为正定矩阵,当0<ω<1时,A+ωP也为正定矩阵.由(12)式可知
(A+ωP)x(1)=b+ωPx(0),
(13)
(A+ωP)x(2)=b+ωPx(1),
(14)
(14)式减(13)式,得
(A+ωP)(x(2)-x(1))=ωP(x(1)-x(0)),
(15)
记z(k)=(x(k+1)-x(k)),则(15)式可以写成(A+ωP)z(1)=ωPz(0),进而可得(A+ωP)z(k)=ωPz(k-1),即
z(k)=(A+ωP)-1ωPz(k-1)=(A+ωP)-1ωP((A+ωP)-1ωPz(k-2))=
ω2((A+ωP)-1P)2z(k-2),
依次迭代下去,得
z(k)=ωk((A+ωP)-1P)kz(1),
(16)
对(16)式两端同时左乘以(P-1(A+ωP))k,得
(P-1(A+ωP))kz(k)=ωkx(1).
(17)
由(13)式可知,当x(0)=0时,有
(A+ωP)x(1)=b,
(18)
将(18)式代入(17)式,得
(A+ωP)(P-1(A+ωP))kz(k)=ωkb,
显然,当0<ω<1时,有
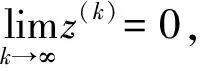
引理[7]若A为正定矩阵,当0<ω<1时,有
cond2(A+ωP) 由式(10),(12),得到新的迭代格式 (19) 迭代终止的条件有两个:一是设置阈值,即对迭代算法需要迭代的次数设置一个上限.它是一种经验式的迭代终止条件,具有很大的不确定性,并且不能保证其有效性和相应的精度.二是引进迭代残差,即前后两次迭代的差小于一个非常小的量,即err(k)=‖xk-xk-1‖<ε.但是,这种方法在求解病态方程组时效果不是很好.基于以上方法,文献[8]提出了一种新的迭代终止准则,即把迭代残差看作是两个过程算法:单调下降过程和单调上升过程,而最为理想的迭代终止点会出现在下降过程到上升过程的拐点处,即迭代终止条件满足err(k)/err(k-1)≥1. Hilbert矩阵的定义采用以下形式 H=(hij)n×n, Hx=b, 其精确解可以取为x=[1,1,1,…,1]. 对于上述例子,在相同条件下,取ω=0.000 01,τ=1e-8,将论文方法与主元加权改善法、新主元加权法的绝对误差和迭代次数进行比较,实验结果见表1,2. 表1 3种方法绝对误差对比 通过表1的实验结果可以看出,论文算法精度要优于主元加权改善法和新主元加权法.通过表2的迭代次数对比可以看出,论文算法的迭代次数要远远小于后面两种方法. 表2 3种方法迭代次数对比 取Vandermonde矩阵[9]为下列形式 其中:x向量的定义为x=H×1,H为与Vandermonde矩阵同阶的Hilbert矩阵,1为元素全为1的列向量,精确解同样取为x=[1,1,1,…,1]. Vandermonde矩阵是一个高度病态的矩阵,阶数比较小时,会出现很大的条件数.下面采用论文提出的求解病态线性方程组的精细积分新主元加权迭代算法对此病态方程组进行求解,并与精确解进行比较,实验结果见表3. 表3 论文算法结果和真解对比 从表3中的实验数据可以看到,Vandermonde矩阵的条件数受阶数的影响非常大,条件数随着其阶数的增加急剧增大,论文的算法所得结果与真解相比达到了令人满意的结果,并且迭代次数比较少. 通过构造一个特殊矩阵,对病态方程组的系数矩阵进行主元加权,并将其与精细积分法相结合,提出了一种新主元加权迭代法和精细积分相结合的方法.数值实验结果表明,和主元加权改善法和新主元加权法相比较,该方法无论在计算精度还是计算效率方面都有提升,是一种有效的求解病态方程组的迭代方法.3 实验结果与分析
3.1 以Hilbert矩阵为系数矩阵的病态方程组的求解
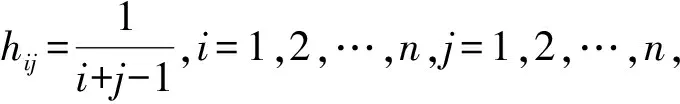


3.2 以Vandermonde矩阵为系数矩阵的病态方程组的求解
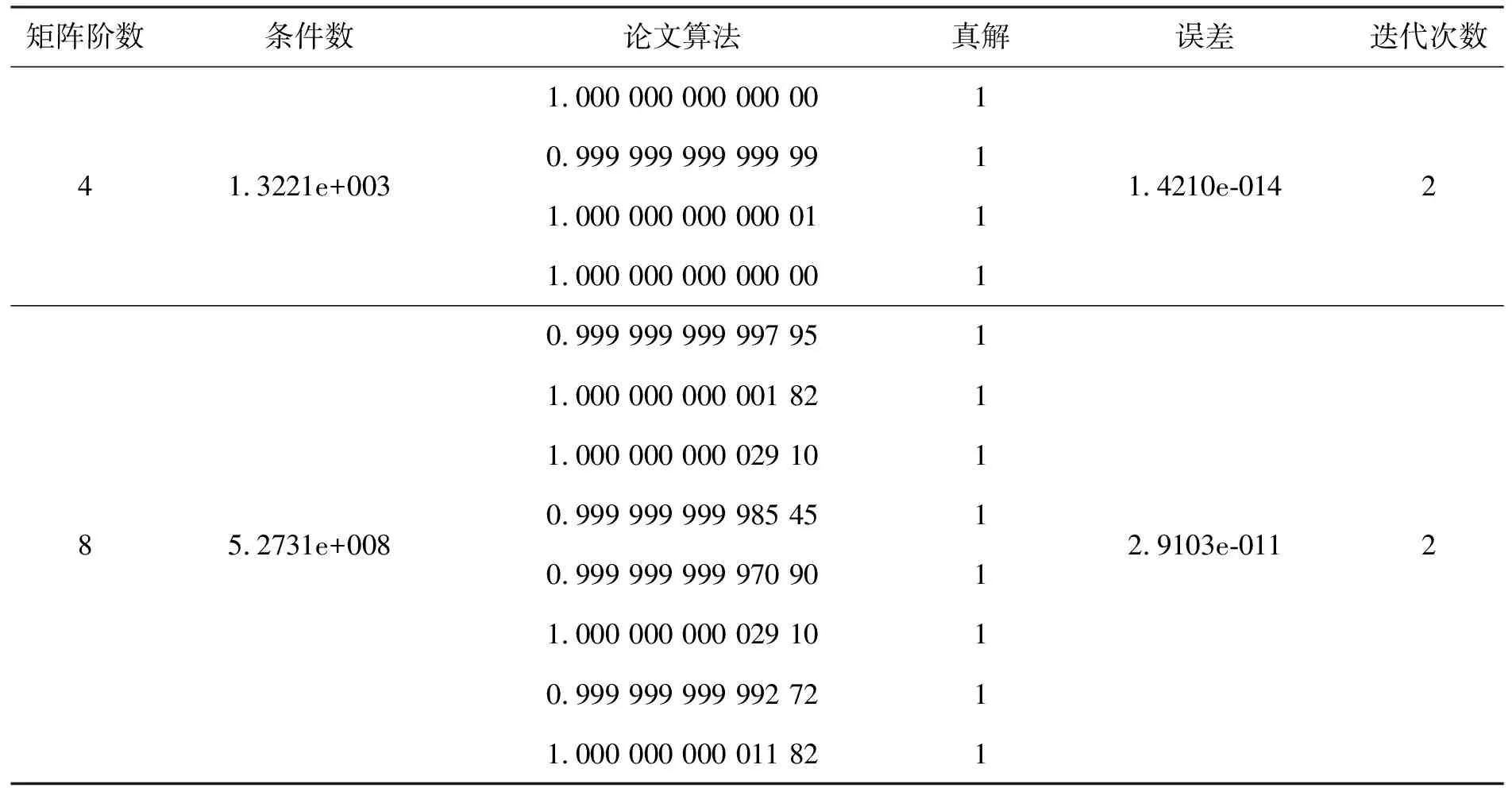
4 结束语
