基于C藤Copula的多维随机环境变量极限状态曲面

涂志斌， 姚剑锋， 黄铭枫， 楼文娟

(1.浙江水利水电学院 建工学院，杭州 310018； 2.浙江大学 建筑工程学院结构工程研究所，杭州 310058)

EC(environmental contour,EC)法是多维随机环境变量联合作用下结构极限荷载效应估计的有效方法，其中心思想是将结构响应与环境变量分开，仅在具有指定超越概率的极限状态曲面上搜索荷载效应极值作为结构极限荷载效应[1]，在海洋工程[2]、地震工程[3]和风工程[4]中有广泛应用。

极限状态曲面是具有相同超越概率的多维随机环境变量组合点的集合，其计算基础为多维随机环境变量的联合分布。常用的联合分布模型有条件联合分布模型、传统联合分布模型和Copula函数。在条件联合分布模型中联合分布表达为主变量的边缘分布和次变量的条件分布，并将条件分布的参数视为主变量的函数，如Huseby等[5-6]、Jonathan等[7]和Saranyasoontorn等[8-9]的研究。由于条件分布的参数与主变量的函数关系不具有普遍性，条件联合分布模型的适用范围受到了限制。传统联合分布模型包含皮尔逊III型分布、Nataf分布等多种分布模型，其特点是将一维分布拓展为多维分布，采用线性相关系数表达变量之间的相关结构，如董胜等[10]、Yue[11]和Silva-González等[12]的研究。然而多维随机变量可能服从不同种类的边缘分布，不满足线性相关关系，传统联合分布模型的应用也具有一定的局限性。Copula函数是一种建立联合分布的工具，可建立具有不同边缘分布和任意相关关系的多维随机变量联合分布函数，并将Gumbel分布、Nataf分布等多种分布纳入其中[13]。涂志斌等[14]采用二维Copula函数建立高层建筑二维风荷载分量的联合分布。Zhang等[15-16]和黄铭枫等[17]采用多种高维Copula函数建立了多风向极值风速的联合分布。为弥补多维Copula函数采用同种函数结构表达各变量间的相关关系这一缺陷，Bedford等[18-19]提出了藤Copula。藤Copula将多维Copula密度函数表达为一系列二维pair Copula密度函数的乘积，且每个pair Copula可选用不同的二维Copula函数。常用的藤Copula有C藤Copula和D藤Copula[20]，其中C藤Copula在海洋工程、土木工程和金融工程等领域的应用更为广泛。Montes-Iturrizaga等[21]以有效波高为主变量，平均风速和谱峰周期为次变量，采用3种二维Copula链接成C藤Copula建立联合分布；樊学平等[22]采用二维Gaussian Copula链接成C藤Copula 考察了天津富民桥主梁5个截面极值应力的相关性；陈好杰等[23]采用5种二维Copula链接成多种C藤Copula讨论了3个大型风电场群之间的出力相关性；李磊等[24]利用C藤Copula估计了连续几个交易日收益率之间的自相依结构。以上研究表明当多维随机变量由一个主变量和多个次变量组成时，基于C藤Copula的多维随机变量联合分布模型能较好地表达各变量之间的相关结构。

极限状态曲面构造的一般方法为Rosenblatt变换。该方法先根据可靠指标在标准正态空间中构造极限状态曲面，再将其映射到物理空间中。根据该变换Silva-González等、Valamanesh 等[25]和Li等[26]构造了不同海域平均风速、有效波高和谱峰周期的极限状态曲面。然而采用Rosenblatt变换构造极限状态曲面涉及条件分布函数的求解和求逆，当多维随机变量的联合分布较为复杂时，以上计算难以实施。

本文提出了基于C藤Copula函数的多维随机变量极限状态曲面计算公式及数值算法，结合风浪同步观测数据构造了平均风速、有效波高和谱峰周期的极限状态曲面，提出了根据极限状态曲面等值线设置风浪参数组合值，讨论了不同Copula函数对极限状态曲面和组合值的影响，并得到几点有益的结论可供海洋结构设计参考。

1 Copula函数的基本理论

设X=(X1,X2,…,Xn)为n维随机环境变量，其边缘分布为Fi(xi)(i=1,…,n)；n维随机变量U=(U1,U2,…,Un)在[0,1]n范围内独立均匀分布，且ui=Fi(xi)；若Fi(xi)单调连续，那么根据Sklar定理，X的联合分布函数F(x)可表达为[20]：

F(x)=C[F1(x1),F2(x2),…,Fn(xn)]=

C(u1,u2,…,un)

(1)

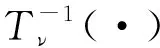
表1 常用Copula函数

设c(u)为Copula密度函数，其表达式为

(2)

X的联合概率密度函数f(x)与c(u)的关系为

f(x)=f(x1,x2,…,xn)=

(3)

(4)

2 基于C藤Copula的联合分布模型

2.1 联合分布模型

藤是藤Copula的链接方式，由树、节点和边构成，不同藤的逻辑结构有所不同。对于5维(n=5)随机变量，C藤的逻辑结构如图1所示。

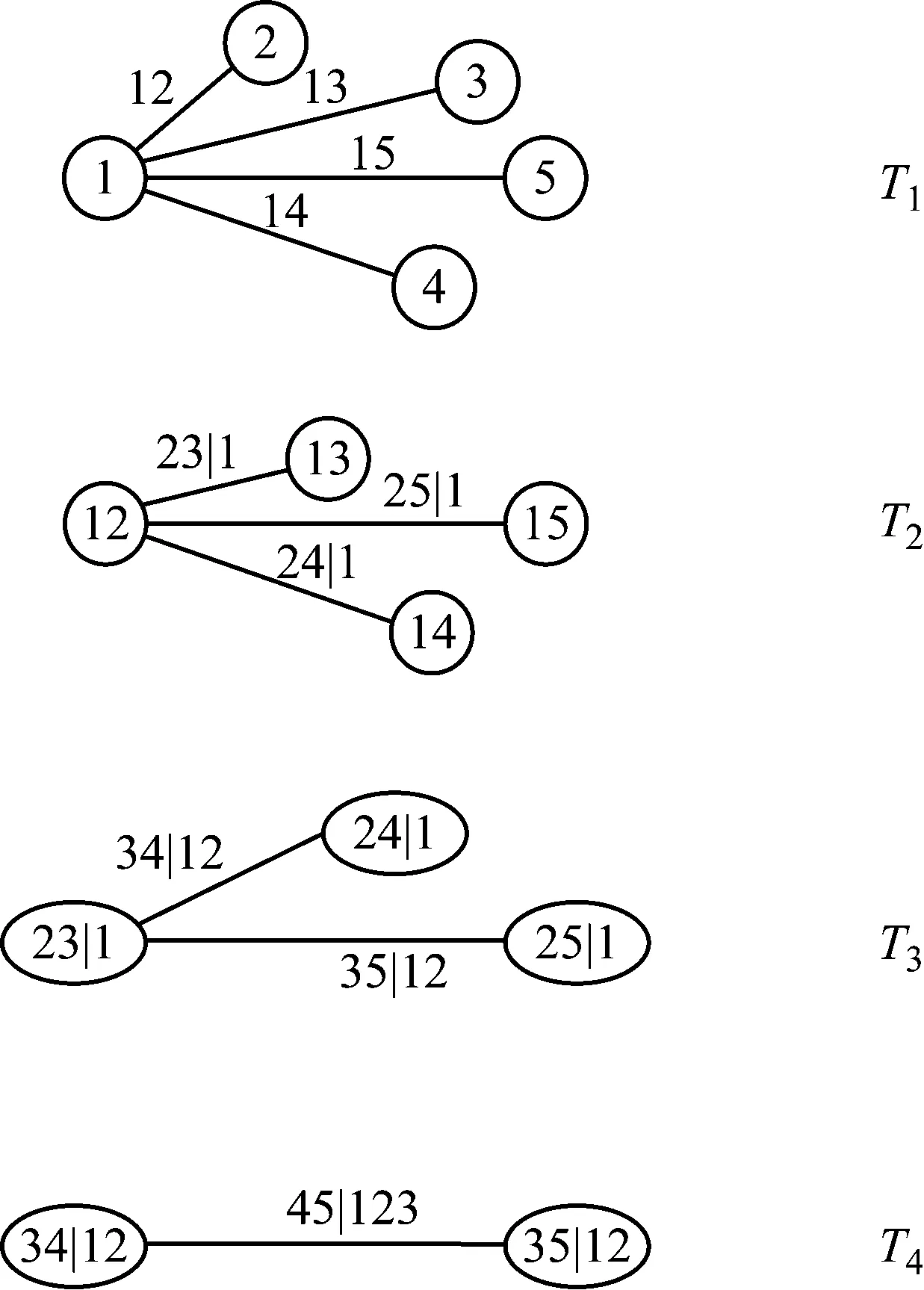
图1 n=5时C藤的逻辑结构图

(5)

式中，cj,j+i|1,…,j-1为变量Xj和Xj+i基于变量X1,…,Xj-1的二维Copula密度函数，表达了变量Xj|X1,…,Xj-1与变量Xj+i|X1,…,Xj-1的相关结构。将式(5)代入式(3)，n维随机变量的联合概率密度函数可表达为

(6)

(7)

特殊地，对于二维随机变量，式(7)可写作

(8)

式中，α21为F1(x1)和F2(x2)的相关参数。对于三维随机变量，式(7)可写作

(9)

2.2 参数估计

⋮

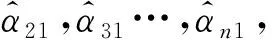
(10)

⋮

(11)

2.3 最优Copula

在众多Copula函数中，为C藤中的每一条边指定最优Copula作为二维pair Copula。在采用相同边缘分布的前提下，最优Copula能准确表达变量之间的相关结构。目前常用的最优Copula评价准则为AIC准则，其计算公式为

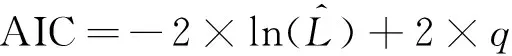
(12)

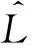
3 基于C藤Copula的极限状态曲面

设Z=(Z1,Z2,…,Zn)为标准正态空间中相互独立的n维随机变量。当超越概率为Pe时，在标准正态空间中极限状态曲面可表达为

|z|=β

(13)

式中，β为可靠指标，β=-Φ-1(Pe)。对于三维变量，在球坐标系中式(13)可写作

z1=βsinθcosφ

z2=βsinθsinφ

z3=βcosθ

(14)

式中，θ和φ分别仰角和方位角。根据Rosenblatt变换，物理空间中的极限状态曲面与标准正态空间中的极限状态曲面一一对应，且具有相同的超越概率，可表达为

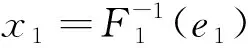
(15)

其中ei=Φ(zi)。对式(15)进行改写，可得：

(16)

将式(7)代入式(16)

e1=F1(x1)

⋮

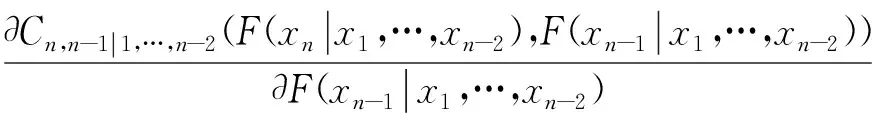
(17)

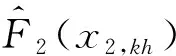
在式(17)中，多维变量的联合分布模型由C藤Copula函数建立，Rosenblatt变换表达为二维Copula的偏导数并采用数值算法求解，避免了式(15)中高维条件分布函数的求解和求逆，具有良好的可行性。

4 工程应用

4.1 风浪实测数据及样本选取

本文以纽约东海岸附近63115号海洋观测站(北纬40.50°，西经-72.92°)的风参数和波浪参数观测记录为统计样本。各参数同步记录，每小时记录一次。提取有效波高日极值Hs及平均风速v、谱峰周期Tp、风向φv及波向φH同步值作为分析样本。图2为风向与波向之差(φv-φH)的角直方图。图2表明风向和波向的差异较小。根据IEC规范[29]和Zhang等[30]的建议，当风向和波向差异较小时，在风浪联合作用分析中可认为风向和波向保持一致。将波向归类到8个角度区间，其玫瑰图如图3所示。由图3可知，波向记录在SE、S、SW和W方向上的频率较高，分别为14.28%、21.48%、16.98%和16.71%，而在NW、N、NE和E方向上的频率较低，分别为8.75%、8.48%、7.81%和5.51%。由于波向与风向的偏差较小，图3近似表达了风向在各方向上的分布频率。由于S方向风浪参数的分布频率较大，选择该方向的统计数据作为分析样本。

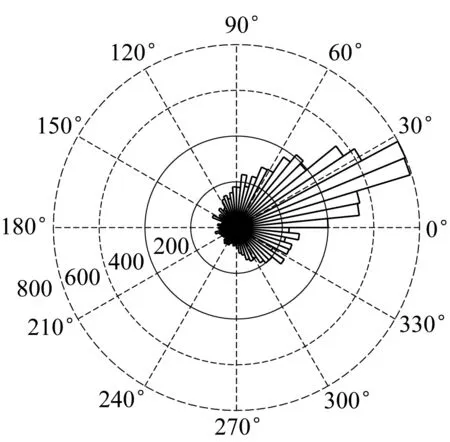
图2 风向与波向之差角直方图

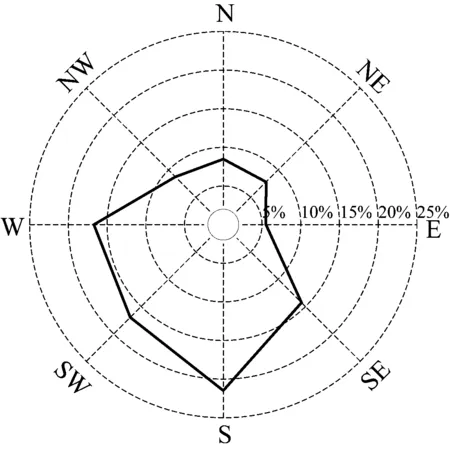
图3 波向玫瑰图

图4为S方向有效波高日极值与平均风速、谱峰周期同步值散点图，表2为3变量的Pearson线性相关系数。由表2可知，有效波高与平均风速有较强的正相关性，与谱峰周期有较弱的正相关性，平均风速与谱峰周期有较弱的负相关性。因此采用C藤Copula构造风浪参数的联合分布模型时取(X1,X2,X3)=(Hs,v,Tp)。

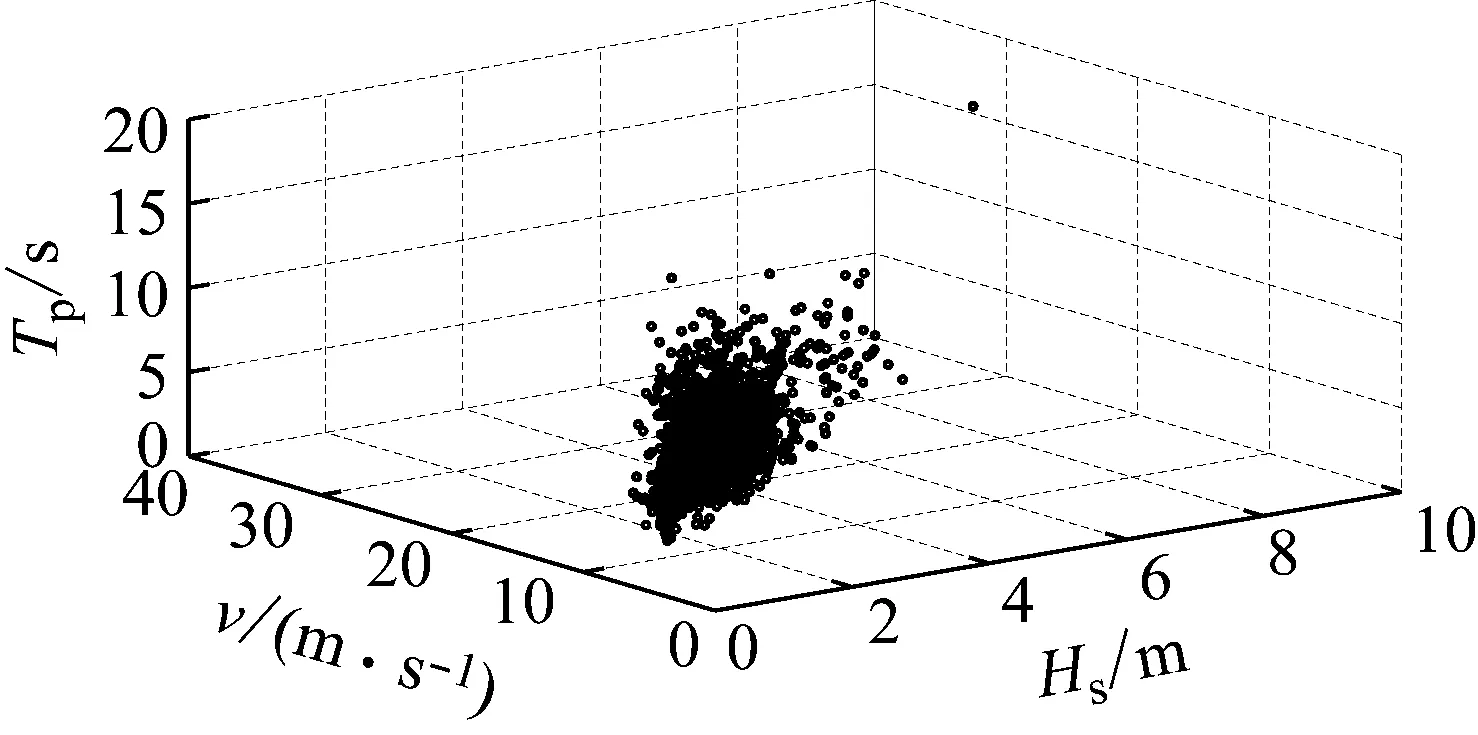
图4 S方向有效波高日极值及平均风速、谱峰周期同步值散点图

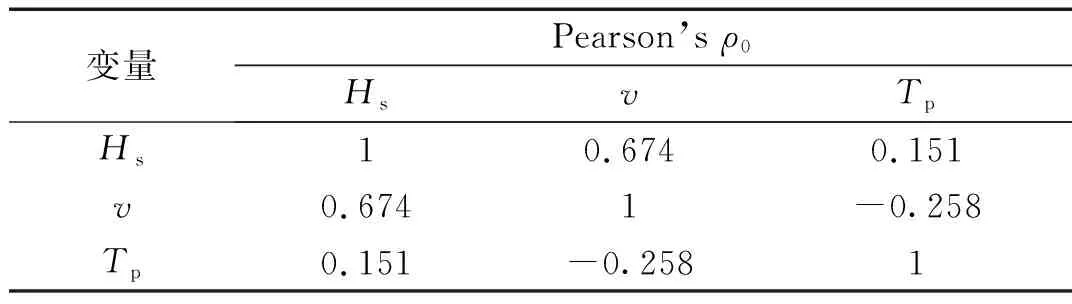
表2 S方向风浪参数的相关系数

4.2 边缘分布拟合

采用Lognormal分布拟合有效波高的边缘分布，采用Weibull分布拟合平均风速和谱峰周期的边缘分布，表达式如式(18)和(19)，拟合结果如图5所示。

Lognormal：

(18)

Weibull：

(19)

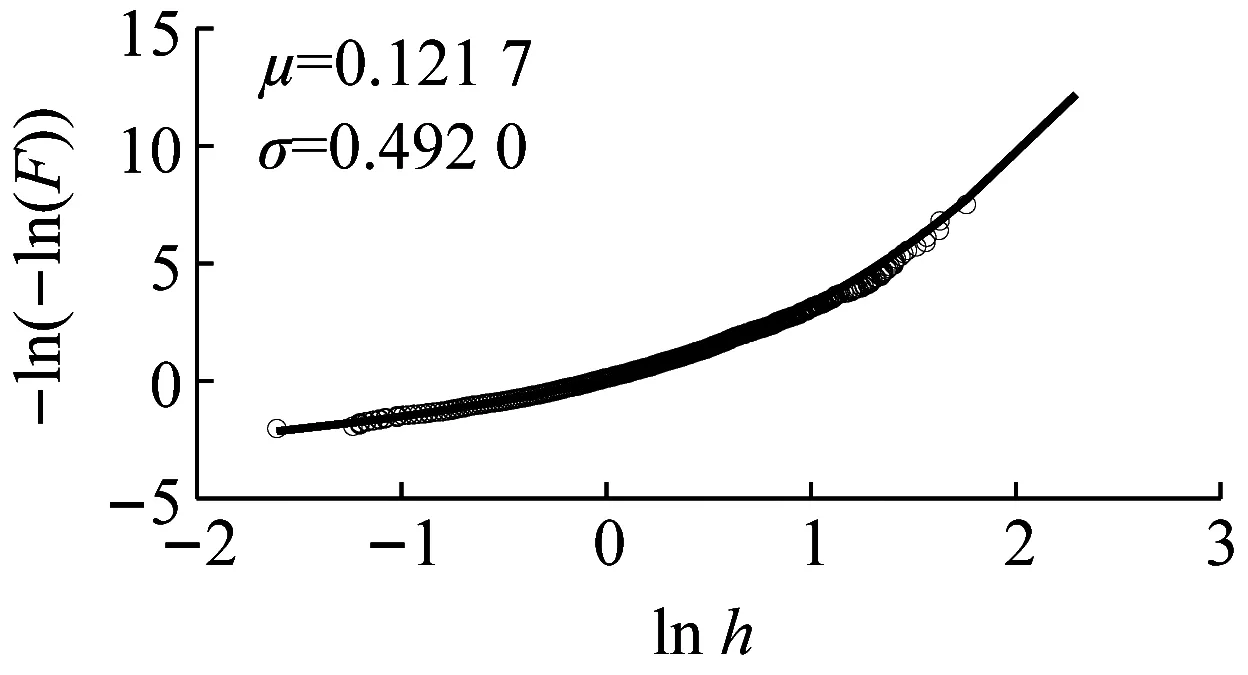
(a) 有效波高

4.3 风浪参数联合分布模型

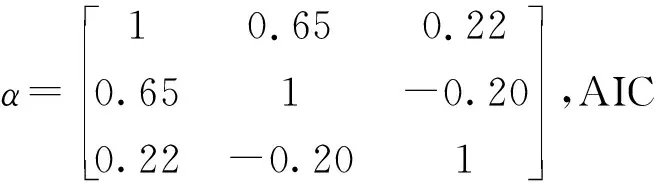
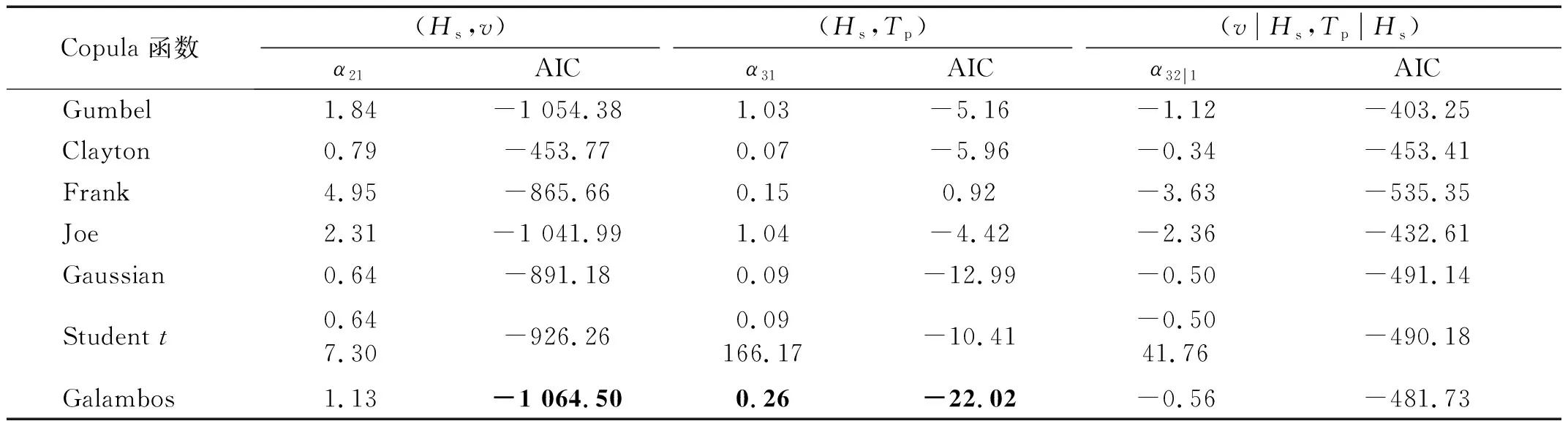
表3 风浪参数联合分布模型参数估计值及AIC值

4.4 风浪极限状态曲面

由于有效波高日极值的统计时长为24 h，重现期T与超越概率Pe的换算关系为

Pe=1/365.25/T

(20)

因此T=20 a时Pe=1.37×10-4，可靠指标β=-Φ-1(Pe)=3.64。在[0,π)和[0,2π)范围内对仰角θ和方位角φ进行均匀离散，离散点数分别为d=60、r=120。分别根据数值算法和参考文献[12]计算基于C藤Copula和三维Gaussian Copula的三维风浪参数极限状态曲面，结果如图6和7所示。曲面上各点为T=20 a时可能发生的平均风速、有效波高和谱峰周期组合。由于相关结构不同，两种Copula构造的极限状态曲面不同，特别是在中部右侧处，前者凸出，后者凹陷。考察曲面形状对风浪参数极值的影响，结果如表4。其中Hs,20、v20和Tp,20分别为T=20 a时有效波高、平均风速和谱峰周期的极值。由表4可知，基于C藤Copula的平均风速极值和谱峰周期极值略微偏小，原因是在C藤Copula中平均风速和谱峰周期的相关性度量样本为基于有效波高的条件经验分布。但总体而言，基于C藤Copula和基于三维Gaussian Copula的风浪参数极值基本与边缘分布一致，受曲面形状的影响较小。

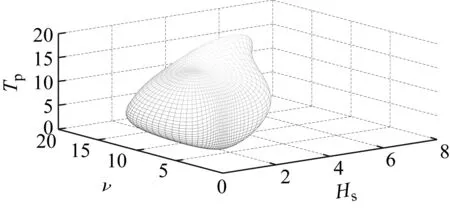
图6 T=20 a时基于C藤Copula的风浪参数极限状态曲面

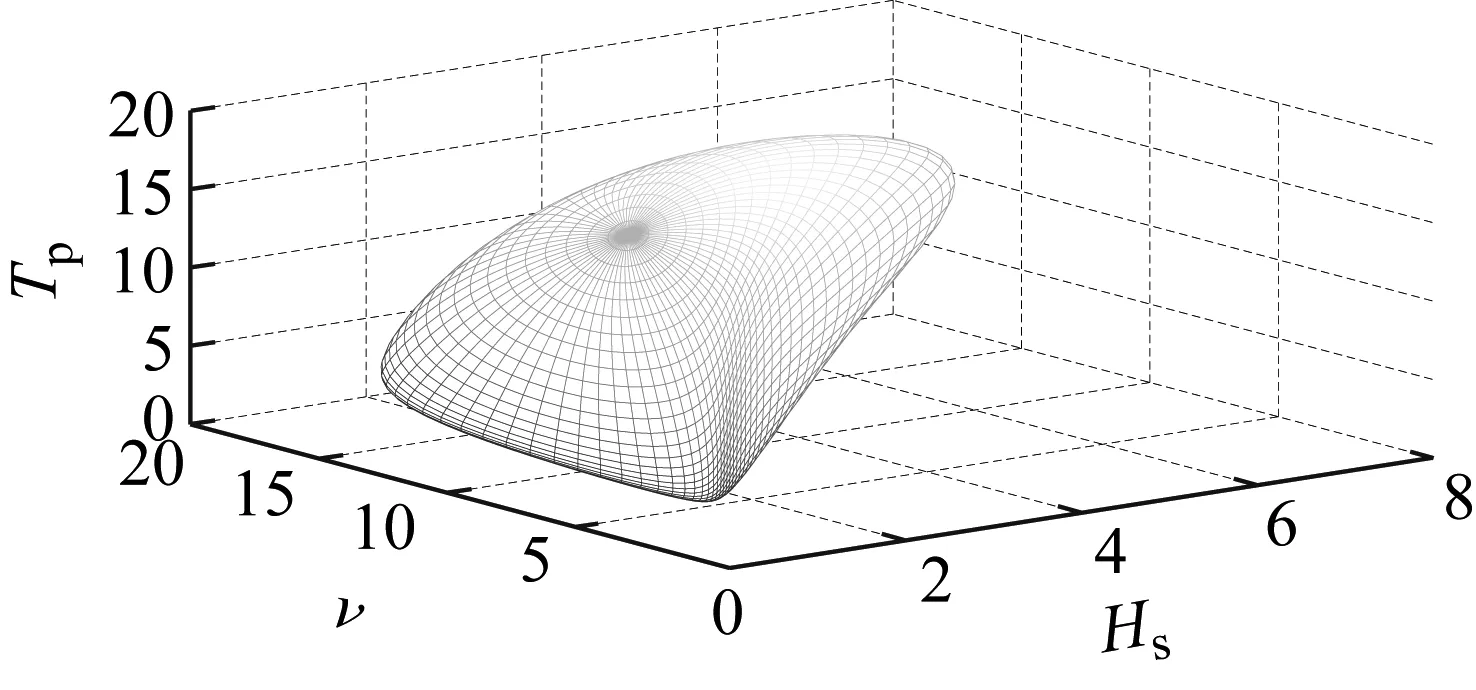
图7 T=20 a时基于三维Gaussian Copula的风浪

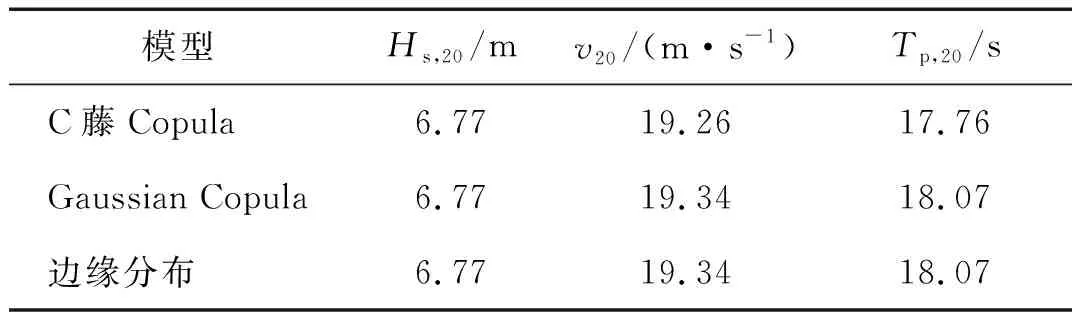
表4 T=20 a时的风浪参数极值

图8为重现期T=20 a时基于C藤Copula的风浪参数极限状态曲面等值线，最大轮廓线为二维风浪参数极限状态曲线，分别由对应的二维最优Copula构造。在图8(a)、(b)中，由于在二维和三维风浪参数联合分布模型中(Hs,v)、(Hs,Tp)的相关结构均采用Galambos Copula表达，相关性度量样本均为各变量的经验分布，等值线分布在二维曲线形成的外包络内；在图8(c)中尽管在二维和三维联合分布模型中(v,Tp)的相关结构均采用Frank Copula表达，但前者的相关性度量样本为经验分布，后者为条件经验分布，导致等值线不再分布在二维曲线内，而是略有超出。

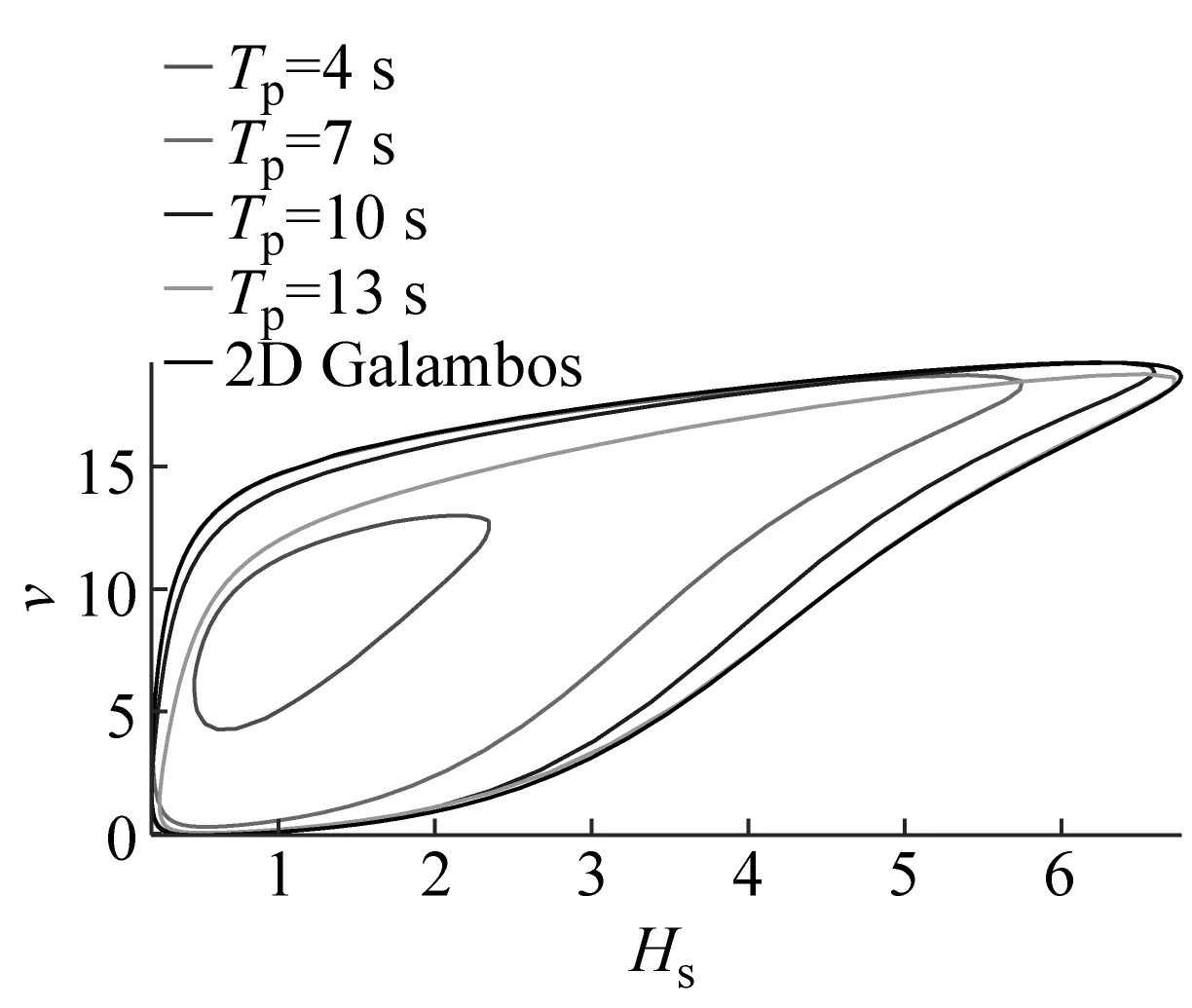
(a) 固定Tp

图9为重现期T=20 a时基于三维Gaussian Copula的风浪参数极限状态曲面等值线，最大轮廓线与图8相同。由于三维Gaussian Copula由二维Gaussian Copula拓展而来，任意两变量的相关结构均由二维Gaussian Copula表达，与二维最优Copula的相关结构差异较大，在图9(a)～(c)中等值线和二维曲线明显不同。造成图8、9不同的原因是，C藤Copula由各变量的最优Copula链接而来，在局部和整体均能最优表达变量间的相关性，由此形成的极限状态曲面有效纳入了二维变量的相关结构，其等值线的外包络是二维极限状态曲线；而三维Gaussian Copula仅在整体上最优表达了各变量的相关性，不能顾及局部，由此形成的极限状态曲面也不能准确纳入二维变量的相关结构。因此对于三维及高维变量，更适合采用C藤Copula建立联合分布模型。

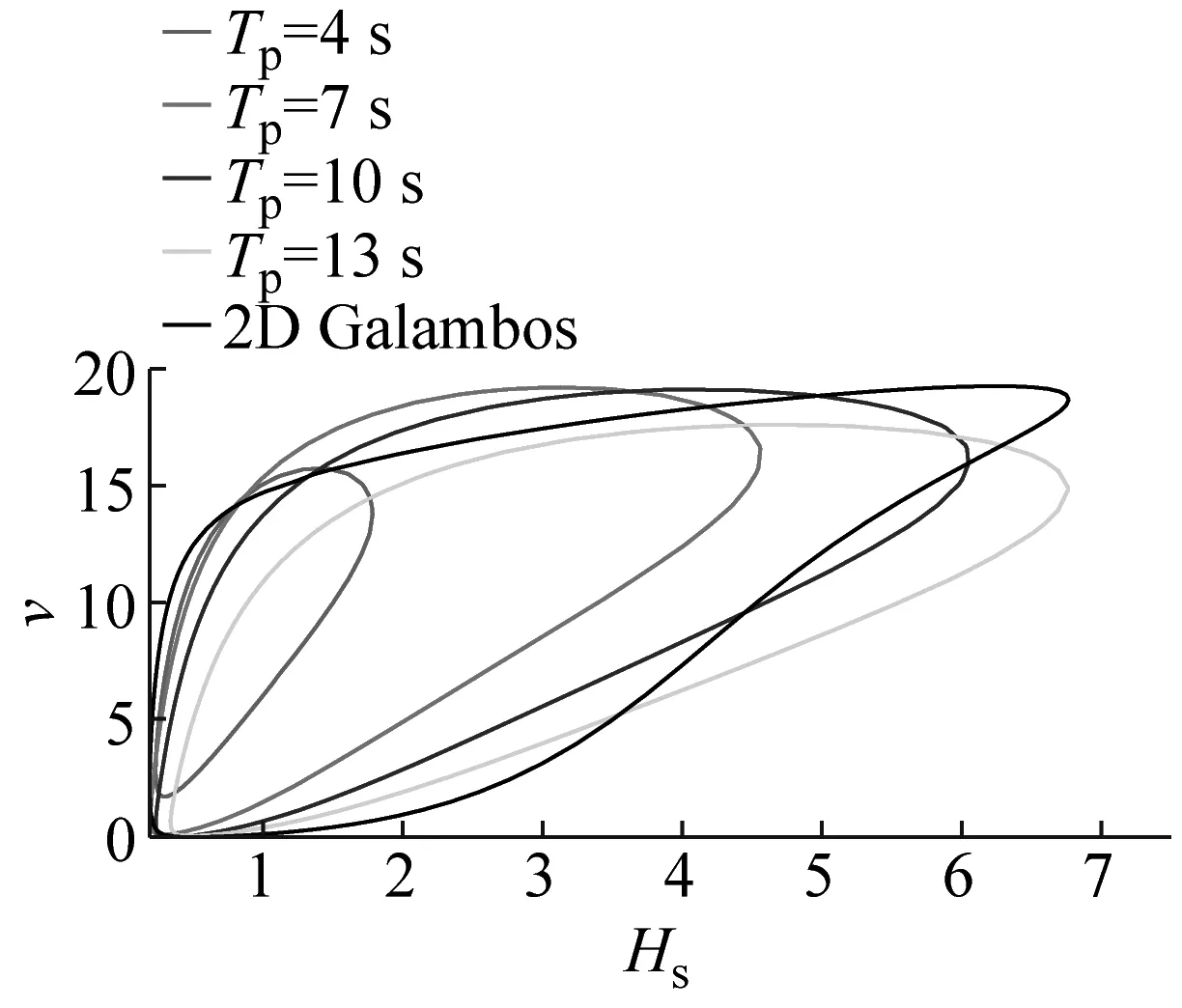
(a) 固定Tp

在EC法中，结构荷载效应计算仅在极限状态曲面上可能产生极限荷载效应的随机变量组合点处进行。为了保证风、浪参数各自及联合重现期，本文提出在使平均风速取极值的等值线上设置风浪参数组合值。根据基于C藤Copula和三维Gaussian Copula的风浪参数极限状态曲面，提取各自平均风速极值所在的等值线，重现期T=20 a时有效波高、平均风速和谱峰周期的组合值Hs,c、vc和Tp,c如表5所示，其中err为各组合值与基于边缘分布的极值(见表4)之间的误差。由表5可知：①vc即为基于C藤Copula或三维Gaussian Copula的平均风速极值，与基于边缘分布的极值间的误差较小；② 基于C藤Copula的Hs,c有所降低，幅度不超过9%；③ 基于C藤Copula的Tp,c显著降低，幅度接近60%；④ 与风浪参数极值相比，采用极限状态曲面等值线确定的组合值在保证多维变量各自及联合重现期的前提下有所降低，可使结构设计更加经济合理；⑤ 基于三维Gaussian Copula的Hs,c和Tp,c均显著降低，表明极限状态曲面的形状对组合值有较大影响，准确地构造极限状态曲面十分必要。

表5 T=20 a时风浪参数组合值

5 结 论

本文提出了基于C藤Copula函数的多维随机变量极限状态曲面计算公式及其数值算法。在该方法中联合分布模型由C藤Copula函数建立，Rosenblatt变换表达为二维Copula的偏导数并采用数值算法求解。结合风浪同步观测数据构造了平均风速、有效波高和谱峰周期的极限状态曲面，提出了根据极限状态曲面确定风浪参数组合值，讨论了不同Copula的影响，并得到了以下结论：

(1) 与多维Copula函数相比，C藤Copula函数在局部和整体上均能最优表达变量间的相关结构，更适用于建立多维随机变量的联合分布模型。

(2) 基于C藤Copula函数的极限状态曲面有效纳入了二维变量的相关结构，其等值线的外包络是二维极限状态曲线。

(3) 极限状态曲面的形状对风浪参数组合值有较大的影响。与风浪参数极值相比，根据等值线确定的组合值在保证多维变量各自及联合重现期的前提下有所降低，可使结构设计更加经济合理。