上游切角倒角小间距比串列方柱大涡模拟研究

郑德乾， 祝瑜哲， 马文勇， 方平治， 李玉学

(1.河南工业大学 土木工程学院，郑州 450001； 2.石家庄铁道大学 土木工程学院，石家庄 050043；3.中国气象局上海台风研究所，上海 200030)

在城市建设高速发展的时代，土地资源的紧张，出现了大量密集的建筑群体。受到邻近建筑影响，作用在高层建筑上的风荷载与单体建筑结构有明显差异，这种风荷载效应被称为干扰作用[1]。

高层建筑风荷载干扰效应从20世纪70年代起即受到关注[2-4]，随着时代的进步和计算机技术的发展，风洞试验和计算流体力学(CFD)方法被广泛应用于柱间干扰效应的研究[5-6]。其中串列双方柱结构最为常见，对其进行研究在理论与工程应用中具有重要意义。已有研究表明，在间距较小时，下游方柱受到较为严重的干扰，平均风荷载减小，体现为“遮挡效应”[7-8]，对下游方柱的迎、侧风面均造成影响；当间距较大时，上、下游方柱间干扰效应逐渐消失。气动措施能有效地改变结构的风荷载与风致响应，具有较好的适用性[9]，其中改变方柱的角部形状是工程上较常用的气动措施。张正维等[10]利用风洞试验探究了不同的圆角率大小对高层建筑的气动弯矩造成的影响，发现当圆角率低于20%时，顺风向气动弯矩会随着圆角率增大而降低。杜晓庆等[11]通过数值模拟方法，在均匀来流条件下，通过将圆角化单体方柱与标准方柱的结果对比分析，证明了方柱圆角化通过影响流体分离再附，可有效抑制表面风压与气动力。除圆角措施外，切角和倒角措施也能显著降低方柱结构的顺、横风向的风致响应[12-14]。与标准方柱相比，倒角措施可一定程度减弱结构的升力[15]，切角措施可减小结构的阻力[16]。以往关于角部处理对方柱风荷载的相关研究多集中于单体[17-18]，串列方柱干扰效应的研究也大多集中于方柱间距比的影响，角部处理对串列双方柱干扰效应的影响有待进一步深入研究。与基于时间平均的雷诺 (RANS)方法相比，基于空间平均的大涡模拟(large eddy simulation，LES)方法能更好的捕捉流场的脉动信息，在方柱绕流方面得具有更好的适用性[19-20]。

本文采用大涡模拟方法，以间距比(方柱中心距和边长的比值)为2.0的串列双方柱为例，分别考虑上游方柱无角部形状变化、切角和倒角(角部变化率10%)对小间距下串列双方柱气动干扰效应的影响，从结构周围平均与瞬态流场角度，探讨角部修正措施对小间距下串列方柱表面风压分布和气动性能的影响机理。

1 计算模型及参数设置

数值模拟中，两方柱边长均为D=0.1 m，以方柱中心距L和边长D定义的间距比为S=L/D=2.0；上游方柱分别考虑了：无角部形状变化，切角和倒角处理，下游方柱始终为标准方柱，如图1所示。为便于分析描述，本文分析中分别采用“标准方柱”、“切角方柱”和“倒角方柱”命名上述3种串列方柱工况。

计算域设置为40D×15D×4D(流向×展向×竖向)，如图1所示。入口采用均匀来流速度条件，以来流平均风速U0和方柱边长D定义的雷诺数Re=22 000；出流面采用压力出口边界条件，计算域两侧采用对称边界，方柱表面为无滑移壁面。压力-速度耦合采用SIMPLEC求解算法；时间离散采用二阶隐式格式，时间步长0.000 5 s；空间离散采用具有二阶精度的Bounded central differencing格式；亚格子模型采用标准Smagorinsky-Lilly模型。

(a) 计算域整体和边界条件

计算域的离散采用非均匀结构化网格，结构附近网格加密，为考察近壁面网格尺寸的影响，以无角部处理的标准串列双方柱为例，分别选用3套不同密度的近壁面网格进行大涡模拟计算，并将模拟结果与标准方柱风洞试验[21]进行了对比分析，详细网格参数如表1所示。

表1 间距比S=2.0串列方柱气动力系数对比

2 结果与讨论

本文的升、阻力系数CL、CD定义为

(1)

(2)

式中:ρa为空气密度;U0为来流风速;FL、FD分别为升、阻力。脉动升力系数和平均阻力系数分别采用升力系数根方差CL,rms和阻力系数均值CD,mean表示。方柱表面风压系数Cp采用下式无量纲处理，即：

(3)

方柱表面的平均和脉动风压系数分别采用风压系数平均值Cp,mean和根方差值Cp,rms表示。

斯特罗哈数定义为

St=fD/U0

(4)

式中，f为旋涡脱落频率，Hz。

2.1 数值模拟结果验证

为说明本文数值模拟方法及参数设置的有效性，将大涡模拟所得标准方柱的气动力系数与文献试验结果进行了对比，如表1所示，表中“/”两侧数据分别表示上、下游方柱气动力系数统计值。图2为标准方柱大涡模拟所得平均、脉动风压系数与风洞试验结果的比较，图中“上游方柱”测点编号范围1～41，“下游方柱”测点编号范围50～90。由表1和图2可见：

(a) 平均风压系数

(1) 在气动力系数方面(表1)，不同网格情况下，大涡模拟所得上、下游方柱的气动力系数统计值与文献[21-22]试验结果均具有较好的一致性，其中Mesh3网格上、下游方柱的平均阻力系数和脉动升力系数与试验结果更为吻合，而下游方柱的斯特罗哈数略高于试验值。

(2) 在风压系数方面(图2)，3种网格情况下，大涡模拟所得标准方柱的平均风压系数与试验值均较为吻合；不同网格的脉动风压系数大涡模拟结果，以及风洞试验结果[23-25]之间均存在着一定的离散性，但随测点位置的变化趋势基本一致，其中Mesh3网格的大涡模拟结果与文献试验结果的一致性更好。

综上，本文数值模拟方法及参数能够较好地预测串列方柱的平均和脉动风荷载，其中基于较密的近壁面网格布置和较小的网格伸展率的Mesh3大涡模拟结果与试验结果的一致性更好，因此下文的切角方柱、倒角方柱的大涡模拟计算均采用Mesh3网格参数。

2.2 角部处理对串列方柱风荷载的影响

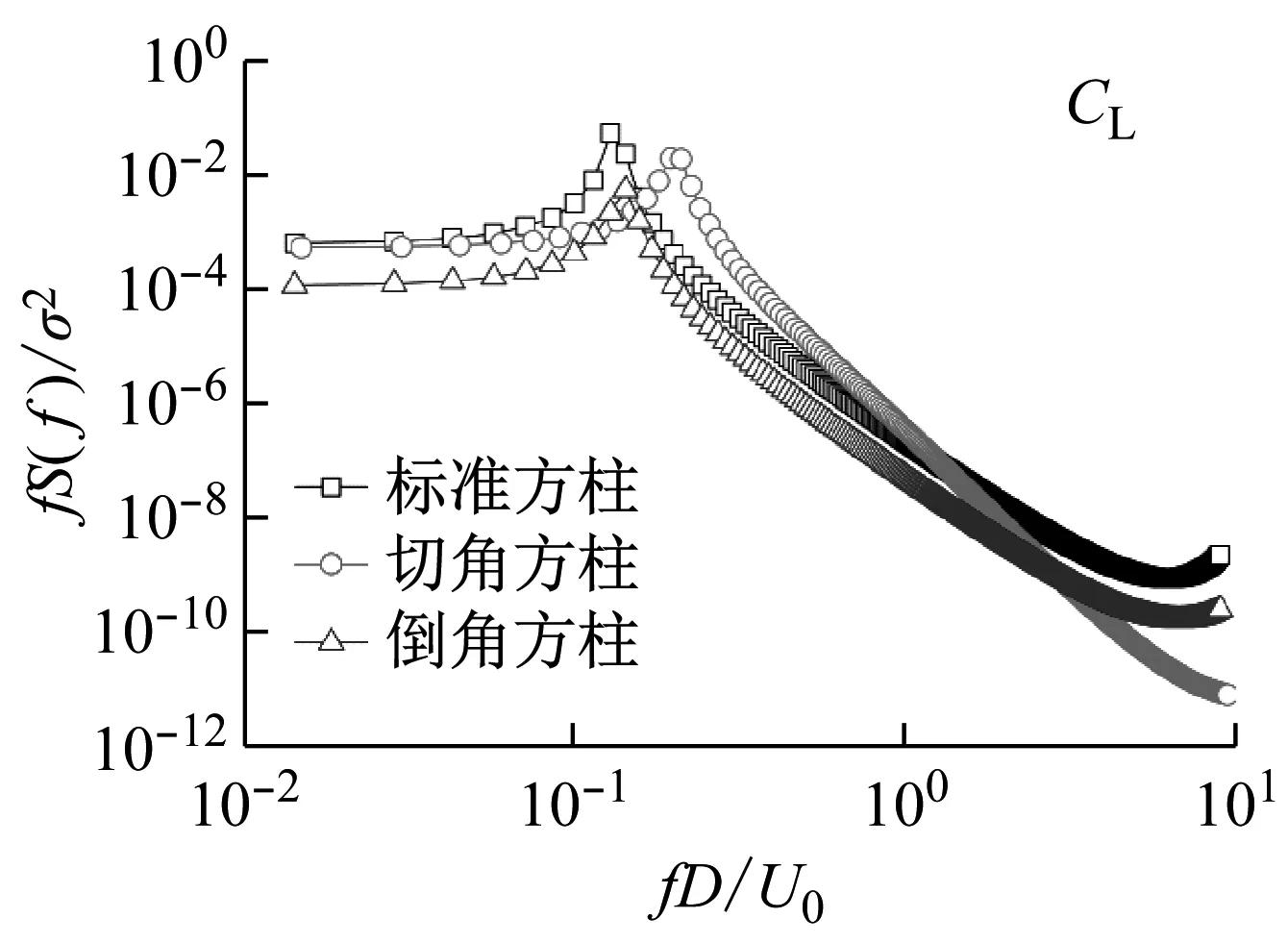
表1给出了Mesh3布置下，大涡模拟所得标准方柱、切角方柱和倒角方柱工况的气动力系数统计值比较，升、阻力系数功率谱的比较如图3所示。

对于气动力系数统计值(表1)，上游方柱切角、倒角后，上、下游方柱的气动力系数与标准方柱相比均有较明显的差异。与标准方柱相比，具体变化情况为：对于上游方柱来说，切角方柱和倒角方柱工况的平均阻力系数分别降低了31.0%和24.5%；在脉动升力系数方面，切角对方柱的脉动升力系数影响可以忽略，而倒角方柱则从0.10降至0.04，降幅达60%；斯特罗哈数值则是切角方柱和倒角方柱工况均有明显提高，增幅分别为52.7%和11.6%。而对于下游方柱来说，切角方柱工况的平均阻力系数和倒角方柱的脉动升力系数变化较明显，分别降低了27.3%和33.3%；切角方柱和倒角方柱工况的斯特罗哈数则分别提高了47.4%和6.6%。

对于气动力系数功率谱(图3)，上、下游方柱的升力系数谱(图3(a)、3(c))均表现为标准方柱的曲线面积最大，倒角方柱次之，切角方柱最小，且方柱升力系数谱的谱峰均发生了偏移，这是由于上游方柱切角和倒角处理措施减小了方柱尾流的宽度，同时减弱了上、下游方柱的涡脱强度，提高了旋涡脱落的频率。对于阻力系数谱来说，上游方柱的阻力系数谱(图3(b))没有明显的峰，这是由于本文研究中不考虑来流紊流，而上游方柱的阻力系数脉动主要来自于来流脉动所致；相比之下，下游方柱阻力系数自谱(图3(d))则存在较明显的峰，这是由于下游方柱处于上游方柱的尾流区，尾流旋涡脱落导致下游方柱产生了“来流”风速脉动，此外，由于上游方柱切角倒角后影响了尾流涡脱，其中切角方柱工况的影响更为显著(请见第2.4节流场分析)，因而下游方柱阻力系数均存在明显的峰且切角方柱工况的峰值频率更高。

(a) 上游升力系数功率谱

为进一步分析上游方柱角部修正对串列方柱局部风荷载的影响[26]，下面选取了大涡模拟所得3种串列方柱1/2H高度表面测点的平均、脉动风压系数进行比较，如图4所示。由图4可见：

(1) 总体上，本文考虑的3种串列方柱工况的平均风压系数分布趋势基本一致，其中上游方柱迎风面为正压(风压力)，侧面和背风面为负压(风吸力)；而下游方柱则因受到上游方柱的遮挡[27]，表面均为负压(风吸力)。具体地，切角方柱和倒角方柱工况的上游方柱角部变化区域存在平均风压系数值突变，在迎风面角部分离点处(第10号测点位置)首先出现较大的负压值，分别为-1.09和-0.93；然后分别在靠近下游的第13号测点和第12号测点位置再次出现较大负压，其中切角方柱工况值为-1.69，倒角方柱为-0.96，该平均风压系数值的突变现象是上游方柱角部形状变化所致，与相同角部修正的单体方柱规律基本一致[28]。

对于下游方柱来说，3种串列方柱工况下其迎、背风面的角部分离区也存在着一定的压力突变(只是没有上游方柱明显)，其中切角方柱工况更为显著；切角方柱工况的侧面平均风压系数也与倒角方柱和标准方柱有较明显的差异，而背风面平均风压系数明显高于倒角方柱，与标准方柱接近，这是由于上游方柱角部形状变化改变了分离点位置，使得剪切流扩散角度发生变化，气流在下游方柱的绕流场受到影响，产生了不同程度的流动再附，导致下游方柱的平均风压系数降低，平均阻力系数也有所减小(表1)。切角方柱工况的下游方柱表面平均风压系数与标准方柱差异最大，说明上游方柱切角对下游方柱的平均风压影响更为显著。

(2) 在脉动风压系数方面，对于标准方柱工况，上游方柱背风面角部分离点处(第31号测点)存在脉动风压系数值的突变，由极大值0.25降至0.15；下游方柱的迎、背风面角部分离点(第60号、第80号测点)再次发生脉动风压系数值突变，极大值分别为0.31和0.42，均高于上游方柱，此外，下游方柱表面脉动风压系数值总体上也均高于上游方柱的相同位置数值，体现了小间距比串列方柱间的相互干扰。

结合图4(a)所示标准方柱工况上、下游方柱的平均风压系数对比结果可知，在本文考虑的间距比情况下，当上游方柱角部形状无变化(标准方柱工况)时，上游方柱的“遮挡效应”已对下游方柱迎风面的平均风压产生显著影响，使其由无干扰时的正压变为负压；对下游方柱脉动风压的影响则是明显增大了“遮挡”后各表面的脉动风压系数值，这是由于其处于上游方柱尾流区，受上游方柱分离涡影响所致。当考虑上游方柱角部形状变化时，切角方柱和倒角方柱工况的下游方柱的第60号、第80号测点均产生脉动压力系数极大值，其中切角方柱分别为0.24、0.34，倒角方柱则分别为0.15、0.23，相比之下，倒角方柱的脉动风压系数值均较小。可见，上游方柱倒角处理能更显著地减弱下游方柱的脉动风压。

(a) 平均风压系数

综上可知，与标准方柱相比，上游方柱采用切角和倒角处理后，对串列方柱的“遮挡效应”造成了明显的影响，导致下游方柱的气动力和风压分布明显变化，这主要是上游方柱角部形状的改变影响了流动分离点位置、剪切流扩散角度以及流动再附现象等，这将在下文流场分析中进一步解释。

2.3 串列方柱周边测点脉动风速谱分析

为了进一步探究上游切角倒角对串列方柱风压分布造成的影响，选取了1/2H高度截面方柱周边测点(图5)的脉动风速谱比较，如图6所示。图5中测点P1、P4分别位于上、下游方柱侧面的中部，距离壁面0.3D；P2、P5分别位于上、下游方柱背风面角点处，距离侧面、背风面壁面均0.1D；P3位于上、下游方柱之间的中心位置；P6位于距离下游方柱背风面1D位置的尾流区。由图6可见：

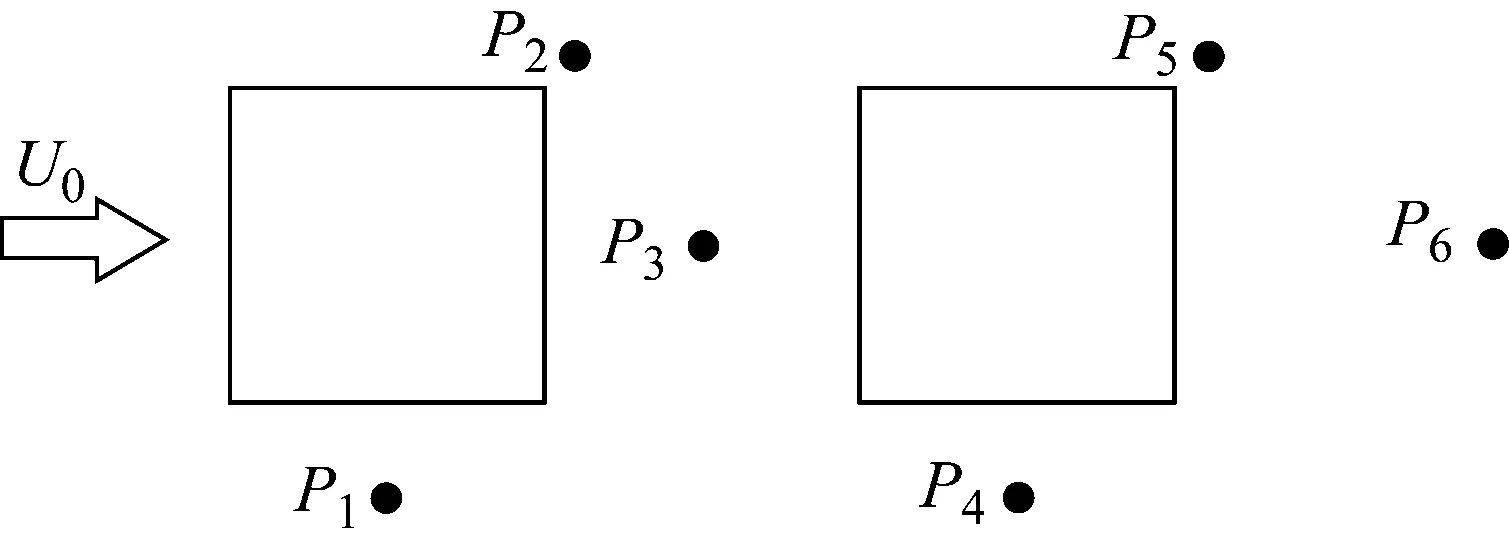
图5 方柱周边测点

(a) P1测点

(1) 对于上游方柱来说，其近壁面位置(测点P1)和两方柱中心位置(测点P3)处，切角、倒角方柱的脉动风速谱峰值明显发生了偏移，对应的旋涡脱落频率高于标准方柱；而在角点位置(测点P2)处，3个串列方柱工况的脉动风速谱曲线形状较为接近，并无明显偏移现象。

(2) 下游方柱的近壁面位置(测点P4)处，切角、倒角方柱的风速谱曲线同样发生了偏移现象，其中切角方柱的偏移现象更为显著；而在下游方柱角点位置(测点P5)与尾流区(测点P6)位置，3种方柱的脉动风速谱曲线形状较为相似，且无明显偏移现象。

以上情况说明，上游切角倒角措施对串列方柱旋涡脱落的影响会随着周边位置的改变而有所不同，总体上，对上游方柱周边区域旋涡脱落的影响要高于下游方柱[29]。

2.4 时均流场分析

图7为本文考虑的3种串列方柱周围的时均流线图，为便于分析，图中还给出了方柱周围的平均风压系数等值线。由图7可见：

(1) 总体来说，3种串列方柱工况的上游方柱两侧分离涡均呈现前缘角部分离而后角贴近的现象，且发展形成了较大尺度的分离剪切层，作用于下游方柱表面后，产生了不同程度的流动再附现象，但再附点位置不尽相同，其中标准方柱再附于距离下游方柱背风面0.08 m(即0.8D)，倒角方柱的相应距离为0.01 m(即0.1D)，这与标准方柱比较接近；而切角方柱则是再附于距离下游方柱背风面0.033 m(即0.33D)，与标准方柱和倒角方柱工况相比，上游方柱分离涡在切角方柱表面的再附现象相对不显著，由此可见，上游方柱的切角处理不仅减弱了上游方柱的平均阻力系数，还极大影响了上游方柱的剪切流在下游方柱表面的再附现象，从而造成切角方柱工况的下游方柱脉动风压系数突变相对不明显(图4(b))，同时，上游切角倒角措施也造成了方柱近壁面区域的脉动风速谱发生偏移，涡脱频率高于标准方柱(图6(a))。

(a) 标准方柱

上游方柱的角部处理会明显改变上游柱体前缘的分离角，其中标准方柱的分离角最大，倒角次之，切角最小。由于小间距比下的分离流不会在上游方柱上再附，因此越小的分离角代表更窄的尾流，也意味着在下游方柱上更早的再附。在来流风速不变的情况下，旋涡脱落频率主要受到尾流区涡对间距的影响，当尾流涡对间距减小，其相互作用增强[30]，因而旋涡脱落频率升高，斯特罗哈数增大。

结合平均风压系数图(图4(a))可知，在小间距比下，两串列方柱间被上游方柱产生的剪切层包裹，下游方柱表面的平均风压系数均为负值，此外，下游方柱迎风面受到较强负压作用，且风压系数绝对值大于背风面，导致下游方柱阻力系数值为负。

(2) 标准方柱工况的上游方柱侧面除形成了剪切层外，还生成了贴近壁面的两个小尺度分离涡；切角方柱和倒角方柱工况的上游方柱剪切层比标准方柱更贴近壁面，仅在上游方柱侧面形成了一个小尺度分离涡，其中倒角方柱在方柱的迎、背风面的角点位置处又分别形成了小尺度涡。在下游方柱的背风面尾流区，3种串列方柱工况均存在两个尺寸大致相等的旋涡，因此通过比较3种串列方柱涡核心的间距大小，就可证明上游切角倒角对方柱尾流区宽度是否起到了缩减效果，其中标准方柱的涡核心距离为0.063 m(即0.63D)而切角方柱和倒角方柱工况为0.048 m(即0.48D)和0.054 m(即0.54D)，分别比标准方柱降低了23.8%和14.3%，说明上游方柱角部形状的变化后分离涡更贴近壁面，导致下游方柱旋涡间距缩短，尾流变窄。

结合3种串列方柱工况的气动力的对比结果(表1)可知，在上游方柱的角部区域，切角、倒角处理减小了方柱的剪切流扩散角，造成下游方柱尾流变窄，使得上、下游方柱的平均阻力系数降低，旋涡脱落频率有所提高，造成切角方柱和倒角方柱工况的斯特罗哈数均高于标准方柱，切角方柱的尾流最窄，因此其斯特罗哈数值最大，但同时，尾流区涡对间距的减小在提升涡脱频率的同时，也使得尾流区能量更加集中，在降低整体平均风压的基础上也会造成局部强负压，因此在下游方柱背风面区域(测点81～90)切角方柱平均风压系数相比倒角方柱接近于标准方柱，比起倒角方柱有明显升高。

2.5 瞬态流场分析

本节通过瞬态涡量图的对比，从涡的形成和发展角度，进一步分析上游方柱角部处理对串列方柱风荷载的影响机理。图8(a)为3种串列方柱的下游方柱局部升力系数时程图，图8(b)为选取的一个涡脱周期内的4个典型时刻，分别用符号“■”、“◆”、“●”、“▲”表示，相应的瞬态涡量分布如图9所示。由图9可见：

(a) 局部升力系数时程图

(1) 气流流经方柱后，沿迎风面两侧发生分离，在本文考虑的小间距比(S=2.0)情况下，两方柱之间的距离不足以形成上游方柱的旋涡脱落，因此3种串列方柱均只在下游方柱尾流区域发生涡脱落，被称为“剪切再附流态”。在上、下游方柱两侧和下游方柱背风面均形成了较为丰富的涡结构，而涡结构和形态及运动态势有所差别。与标准方柱相比，切角和倒角方柱工况因上游角部处理而使得分离涡更加紧贴壁面，下游方柱尾流区涡道更狭窄，而涡道狭窄会造成方柱上下两侧的剪切层在尾流中的相互作用频率增大，从而使得旋涡脱落频率增高，斯特罗哈数St增大。

(2) 与标准方柱相比，切角、倒角方柱的分离涡更多集中于下游方柱周围，上游方柱分离涡的二次再附，减弱了湍流脉动，从而在一定程度上降低了方柱的脉动升力系数。其中，切角方柱工况的尾流区涡道更窄，能量较为集中，尾涡呈现更规则的交替脱落，而增强旋涡脱落的不规则性和减弱旋涡脱落强度是降低矩形高层建筑整体升力的两个措施，因此上游切角措施在降低串列方柱脉动升力方面并未起到显著效果，导致脉动风压系数在下游方柱尾涡区(测点81～86区域)相较标准与倒角方柱有明显升高，同时也导致了切角方柱工况在明显降低平均阻力系数的同时，脉动升力系数与标准方柱相比并无明显变化(表1)。相比之下，倒角方柱工况在尾流区旋涡脱落更加复杂，能量分布更分散，对应的气动力脉动强度更弱。

(3) 对于标准串列方柱的尾流区，在展向较宽范围内均存在旋涡，且旋涡的形成区域较短。由于标准方柱的尾流较宽，使得其旋涡脱落频率较低；旋涡形成区域较短，导致其背风面的负压更强，阻力系数更大。由此可以推断，对于文中考虑的间距比情况，上游方柱前缘的倒角和切角措施会显著影响气流在下游方柱的再附现象和尾流形态，进而能够改变其周围的流场和气动特性，同时也造成了上下游方柱近壁面区域的脉动风速谱发生偏移，涡脱频率高于标准方柱(图6(a)、6(d))。

3 结 论

(1) 本文大涡模拟方法和参数，能够较好地预测串列方柱的平均和脉动风荷载；与风洞试验方法相比，大涡模拟方法便于参数分析，且有利于从流场角度进行干扰效应的机理分析。

(2) 上游方柱切角、倒角处理改变了流体的分离角，从而影响上游分离流在下游方柱的再附位置和尾流状态，其中切角对应的分离角最小，倒角次之，标准方柱最大。在本文选定间距比S=2.0工况下，在上游方柱角部变化区域产生平均风压系数的极大值，降低了平均风压系数，其中上游切角处理对降低串列方柱顺风向平均风荷载效果更突出。

(3) 上游方柱的切角、倒角处理通过提高上下游近侧面区域与柱间区域旋涡脱落的频率，影响了上下游侧面与角点区域的水平脉动风速，其中上游切角措施对串列方柱的影响要高于上游倒角措施。

(4) 上游方柱的切角、倒角处理减小了分离涡与方柱侧面间距，造成背风面处涡距变窄，方柱表面与周边涡脱频率提高。上游倒角处理更有助于发生二次再附，减弱脉动风荷载，能量分布更分散。