基于IDW插值的测量数据等值线生成方法*

2020-07-27胡添毅朱江彦向晋祥周冠男

水运工程 2020年7期

胡添毅，朱江彦，向晋祥，解逊，周冠男

(长江航道测量中心，湖北武汉 430010)

长江是贯穿我国东、中、西部地区的水路运输大通道。《长江经济带发展规划纲要》的审议通过，标志着长江航道需要突破当前瓶颈、承担更多的经济建设与上下游联通工作，因此需要航道单位提供更好、更便捷的电子航道图信息服务。电子航道图的数据基础为内业制图成果，等值线绘制及检查作为内业制图最重要的一环，需要耗费5名内业人员4～5工作日，其效率难以满足快速成图、为电子航道图及时提供数据的需求，亟待提升制作工艺。

目前，在航道测绘中，绘制等值线的基本流程为：1)将测量数据导入CASS软件；2)框选数据生成三角网；3)利用三角网计算生成等值线；4)将该等值线导入清华山维软件；5)在清华山维软件内手动调整等值线；6)将调整的等值线导出为CAD格式。

该绘制流程存在两点不足：1)现有等值线生成流程步骤较多，需要制图人员对CASS、清华山维软件有充分了解，并掌握各项绘图参数，人员培训成本较大；2)手动调整等值线工作量过大，并且在调整过程中可能出现错绘、漏绘等情况。为了提升等值线绘制的效率与准确性，等值线自动生成方法被广泛研究。

大部分的等值线自动生成方法[1-3]基于不规则三角网(triangular irregular network,TIN)模型或其改进模型。王海涛[4]提出一种基于薄板样条函数(TPS)模型构建的等深线生产方法，并通过实际数据验证其有效性。王学潮[5]将测深点网格化后，设计了通过等值点追踪生成等值线、并予以平滑的算法。

本文设计了基于IDW(inverse distance weighted)插值的等值线生成方法，并使用空间查询方法对等值线进行线形优化和拓扑错误修正，最后基于生成和优化方法开发了等值线生成平台。

1 基本方法

在航道测绘作业中，测量得出的水深值或高程值均是在测量区域内处处都有定义的地理特征值，即空间连续数据(spatial continuous data)。为表示完整的河床地形地貌，在源数据中只记录有限个样点值，样点以外各点的值通过插值方法计算。

同时，进行一次测量可能会产生数万个测量点，等值线的生成中需要对这些测量点进行存储、空间查询及计算，以提升等值线计算的效率。本文使用MySQL数据库进行测量点和等值线数据的存储、空间查询与计算。

1.1 插值方法

空间插值方法是基于已知的地理特征点数据，推求同一区域内的未知点的数据。

目前，国内外常见的空间插值方法有IDW插值[6-8]、不规则三角网方法、趋势面(trend)分析法、普通克里格(ordinary Kriging)插值、简单克里格(simple Kriging)插值、泛克里格(universal Kriging)插值等。

IDW插值全称为反距离加权插值，它以插值点与样本点之间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大。

IDW插值的公式为：

(1)

(2)

因为在航道测绘后，测量点经过点位校正在地图上分布均匀，密度也足以在计算中反映河床局部表面变化，本文选取IDW插值方法进行等值线生成的计算。

1.2 MySQL的空间数据库应用

MySQL是一种关系型数据库管理系统[9-10]，MySQL5.7版本遵循OpenGIS联盟(open geospatial consortium，OGC)的几何数据模型规则，对空间数据库进行支持，并支持空间索引[11]，可以提高对数据集空间检索的效率。

空间查询利用空间索引机制，从数据库中找出符合该条件的空间数据，MySQL支持MBRContains()、ST_Contains()、ST_Disjoint()等空间拓扑函数，并可使用ST_PointN(A,n)、ST_Area()、ST_Buffer()等空间数据相关方法。采用MySQL数据库可以有效加快等值线生成平台的计算速度，进而提升内业制图人员的工作效率。

本次研究所用的空间拓扑函数的作用为：MBRContains(A,B),判断几何形状A的最小边界矩形是否包含几何形状B的最小边界矩形；ST_Contains(A,B),判断几何形状A是否完全包含几何形状B(当且仅当B中的所有点都位于A中，并且至少有一个B中的点位于A的内部，为完全包含)；ST_Intersection(A,B),计算几何形状A和B的相交或重叠区域；ST_Disjoint(A,B),判断几何形状A与几何形状B是否有交集；ST_PointN(A,n),返回折线A的第n个点；ST_Area(A)：计算多边形A的面积；ST_Buffer(A,x)：计算生成几何形状A、长度为x的多边形缓冲区。

2 基于ArcGIS的等值线生成流程

本文通过IDW插值算法生成测量区域的等值线图，再从等值线图中提取等值线，根据测量区域的边界进行裁剪。等值线具体的生成流程见图1。

图1 等值线生成流程

将水深测量原始数据进行预处理后，对测深点进行IDW插值计算，得到测量区域的等值面图，并按照高程间距1 m提取等值线。

随后根据测深点计算测深区域边界，计算流程为：1)对每个测深点都生成缓冲区；2)求所有缓冲区的并集；3)将求得的并集生成栅格图层；4)生成栅格图层的线状外接多边形；5)对线状外界多边形进行转换，生成面状外接多边形；6)利用测深区域边界与等值线的拓扑关系裁剪等值线，最终生成裁剪后的等值线。

根据上述等值线生成流程开发等值线生成平台。在Visual Studio环境下，MySQL作为数据库，以ArcGIS Engine工具进行空间数据显示及处理，采用C#语言搭建框架进行开发。

本文的测量原始数据来源于武汉白沙洲桥区2017年9月实地测量数据，测区面积约为7.5万m2,采用多波束测深仪进行河床扫测，采集约3.3万个测深点，并经过数据预处理。等值线生成平台和导入平台的测量原始数据显示见图2，利用上述流程在平台中计算生成的等值线见图3。

图2 等值线生成平台及测量原始数据

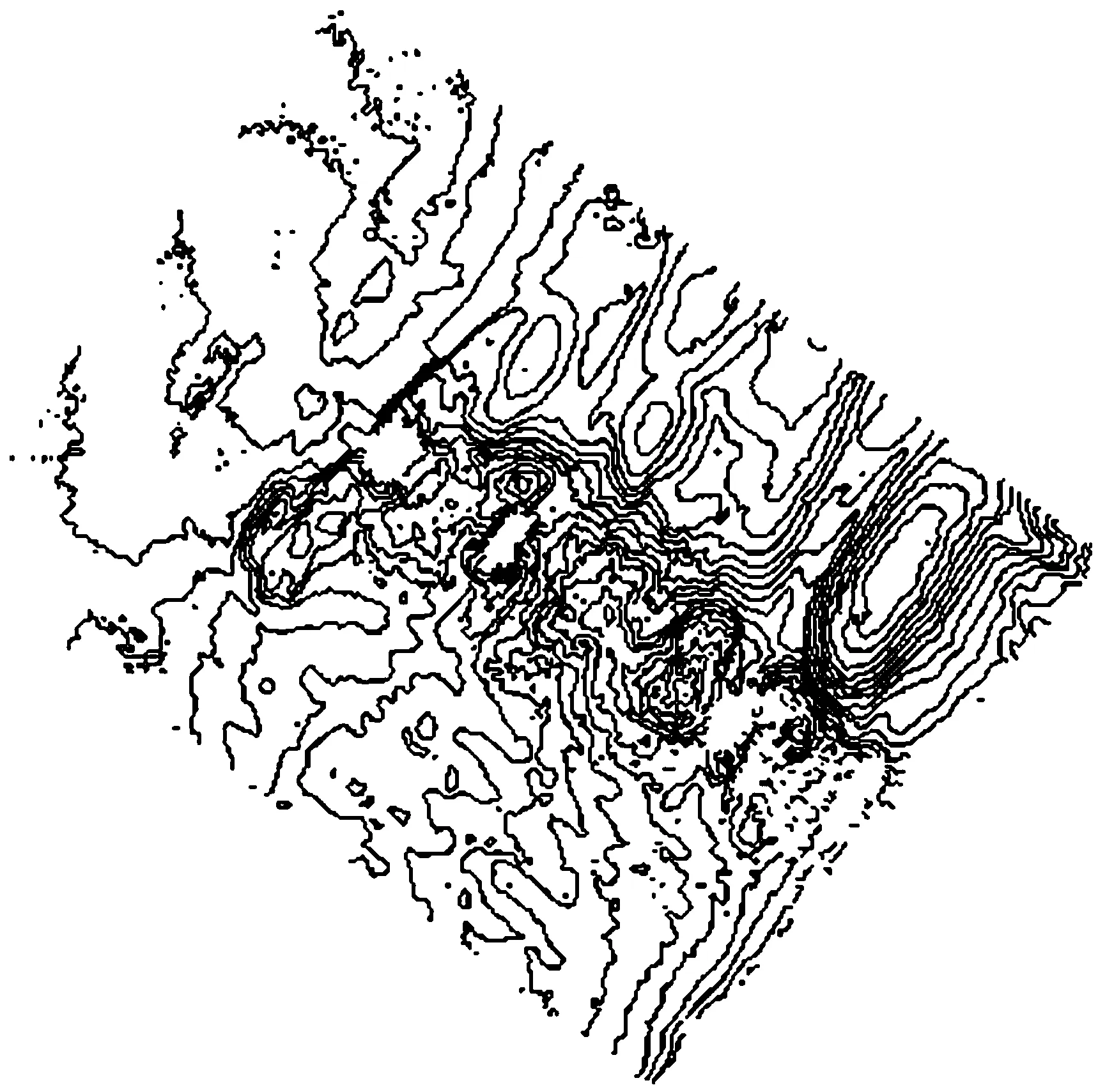
图3 生成的等值线

3 等值线优化方法

3.1 等值线优化需求

为确保等值线可以准确地反映河道地理信息，需要查验等值线与测深点的对应关系，以及等值线自身与等值线之间的拓扑关系。因为水深原始数据的水深或高程值保留一位小数，所以会出现一批值为“x.0”(x=…,-1,0,1,…)的测深点。此类测深点会使生成的等值线与测深点对应关系出现错误，并且在拓扑关系、线形上出现错误，如图4所示，细线为计算生成的等值线，粗线为等值线的理想走向，数字为原始数据的测深值注记。

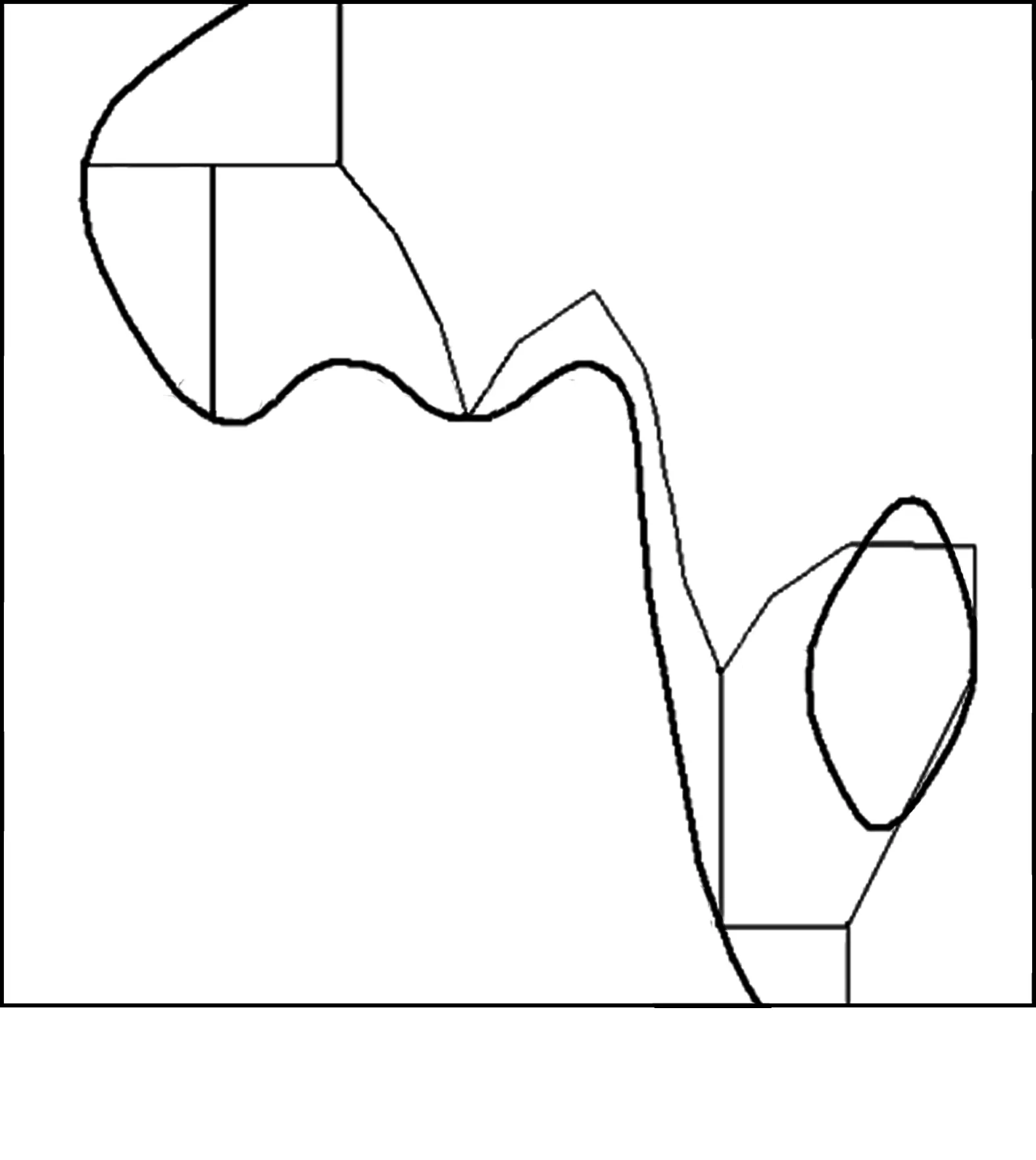
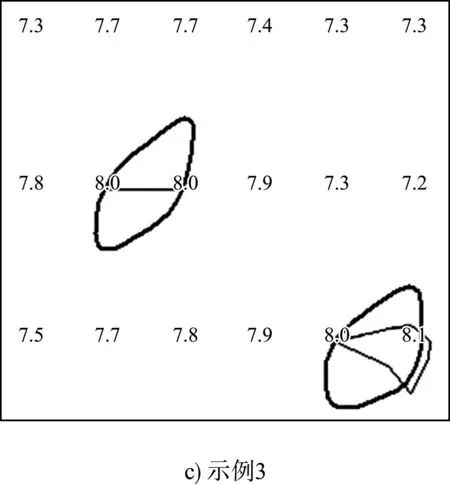
图4 等值线错误状况示例

同时，生成的等值线在线形美观方面相比手工绘制的曲线有较大的差距。如图5所示，需要对曲线部分节点的点位进行校正，并对曲线进行平滑。

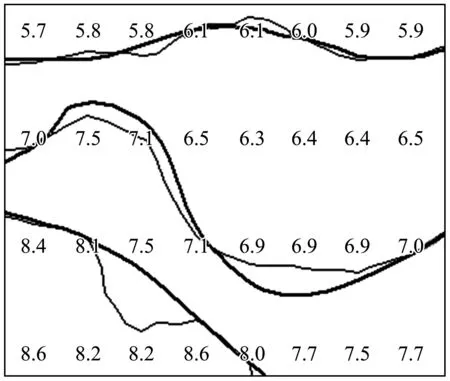
图5 等值线线形优化需求

3.2 特征点与等值线对应关系

此处的特征点是值为“x.0”(x=…,-1,0,1,…)的测深点，为确保等值线与特征点对应关系正确，可以考虑对特征点的部分特征值进行修改，以对IDW插值结果进行修正。

因此，本文根据特征点与周围8个点的数值对比判断是否需要修改特征值，比对步骤为：第一步，利用MySQL的MBRContains()和ST_Buffer()函数生成该点的缓冲区，通过空间拓扑查询获取最邻近的8个点；第二步，根据点的坐标进行排序，最终得到9条点位的记录，特征点与临近8个点的排列顺序见图6；第三步，根据设定规则判断是否修改特征值，部分规则见图7，左边为调整之前的测深点与IDW方法生成的等值线，右边为数值调整之后的测深点与等值线。可以看到，经过数值调整后的测深点生成的等值线可以与特征点有更好的对应关系。

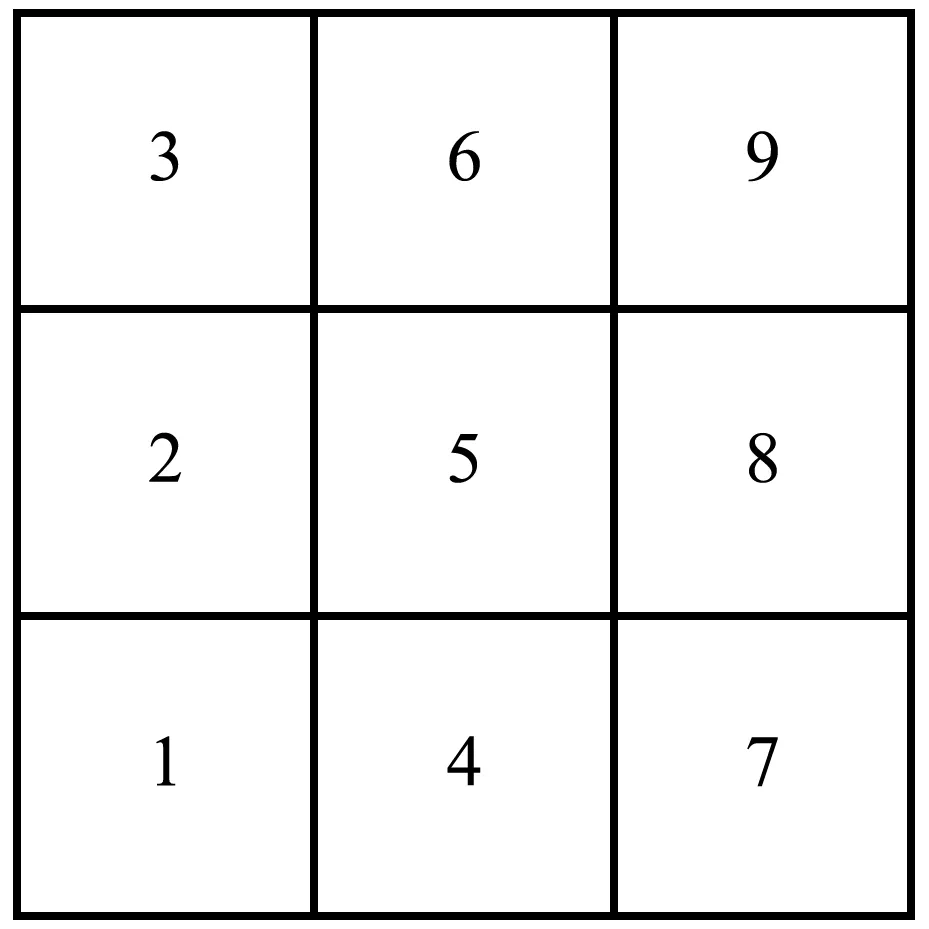
图6 特征点与邻近点点位排序

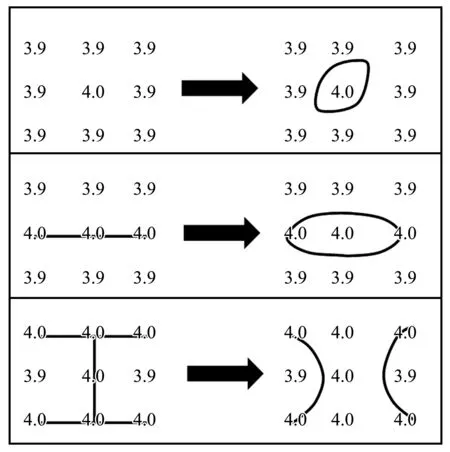
图7 修改特征值部分规则

3.3 等值线优化及平滑

对特征点的值进行修改并通过IDW生成等值线后，需要对等值线的线型进行修改，以使部分曲线准确地反映测深点的高程特征，并使等值线更加美观。

对于节点数超过2的等值线，优化流程为：1)遍历等值线中不是起点和终点的节点；2)空间查询判断节点是否落于测深点上；3)如果否，则查找该节点的上一节点和下一节点；4)计算该节点与上下节点连线的长度；5)根据余弦定理判断该节点与上下节点连线的夹角；6)根据矢量叉积判断该节点是否为拐点;7)如果该节点非拐点，上下节点连线的长度不超过阈值,并且角度小于60°或大于160°，删除该节点。

曲线优化后，利用ArcGIS Engine的Smooth()函数，对曲线进行贝塞尔平滑处理，并且利用Densify()函数增加平滑后曲线的节点密度。等值线优化平滑效果见图8，粗线为优化前的曲线，细线为优化后的曲线，数字为原始数据的测深值注记。

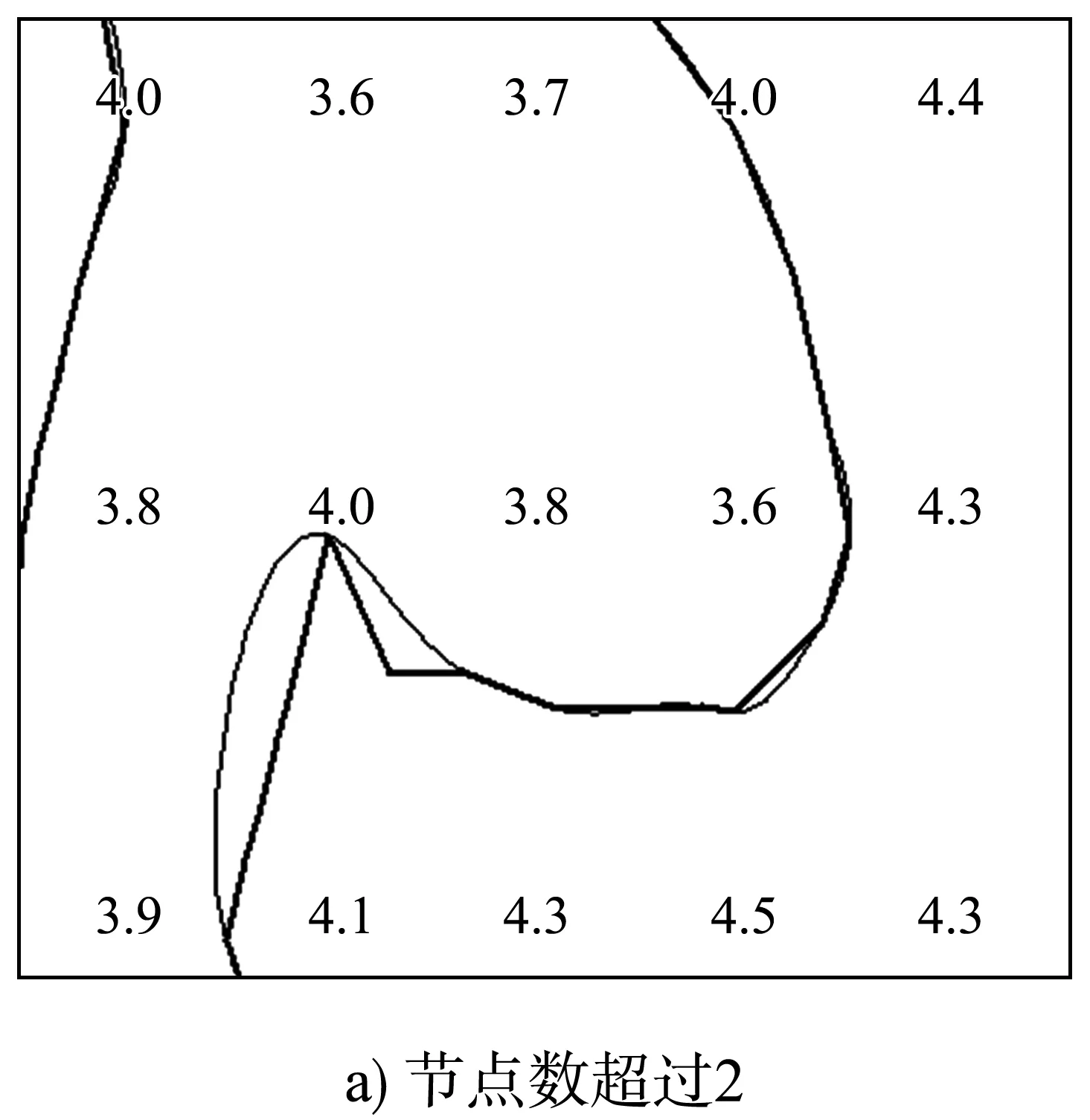
图8 等值线优化平滑效果

3.4 拓扑错误修正

等值线进行平滑处理后，部分曲线的走向会发生改变，在等值线分布密集的区域可能出现相交、重叠等情况，等值线与测深点的对应关系可能发生改变。为了保证等值线图的准确性，需要对等值线进行拓扑检查与修正，检查的图层为经过优化平滑的等值线图层与修改部分特征点特征值的测深点图层。

拓扑检查的内容为：

1)检查线与线之间相互重叠情况，通过MySQL的ST_disjoint()函数判断。

2)检查线与线之间相交情况，通过MySQL的ST_disjoint()函数判断。

3)检查线要素自身重叠或相交的情况，通过曲线的节点遍历查询判断是否有重复节点，若有则说明自身有重叠或相交的情况。

4)检查线要素被特征值不是“x.0”(x=…,-1,0,1,…)的测深点覆盖的情况，通过MySQL的ST_contains()函数判断。

5)检查特征值是“x.0”(x=…,-1,0,1,…)的测深点上没有线要素的情况，通过MySQL的ST_contains()函数判断。

在这里，需要定义元组TopoError(geometryA,geometryB,isclosedA,isclosedB)，其中geometryA和geometryB用来记录发生拓扑错误的形状的id；isclosedA和isclosedB用来记录形状在等值线图的范围内是否闭合，0为闭合，1为不闭合，2表示形状不是曲线。在进行拓扑错误的检查后，将产生拓扑错误的形状记录在TopoError的数组中，并进行拓扑错误的修正，并生成拓扑修正后的等值线图层，拓扑修正流程见图9。

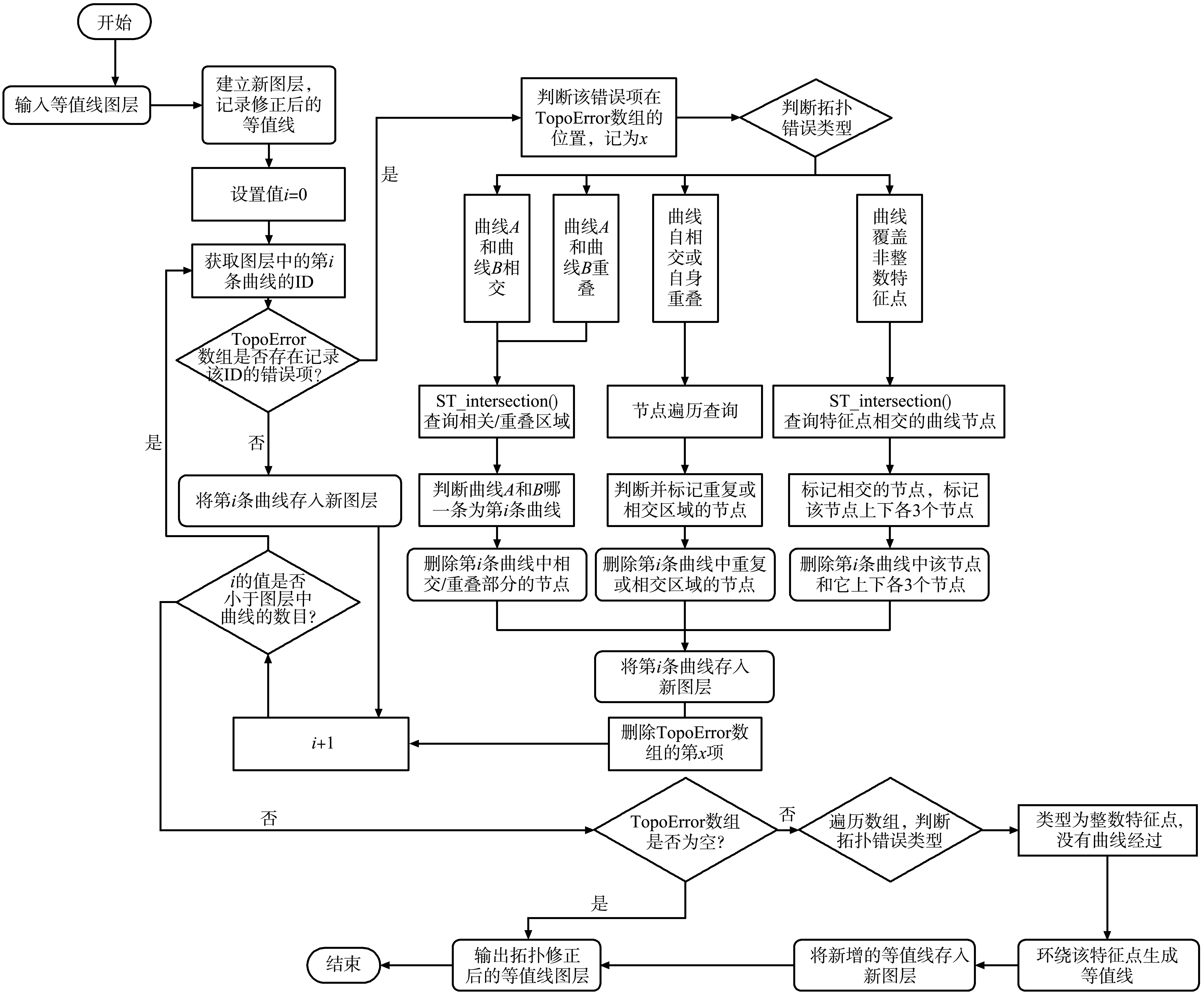
图9 等值线拓扑修正流程

等值线拓扑修正的效果见图10，细线为修正前的曲线，粗线为修正后的曲线，数字为原始数据的测深值注记。

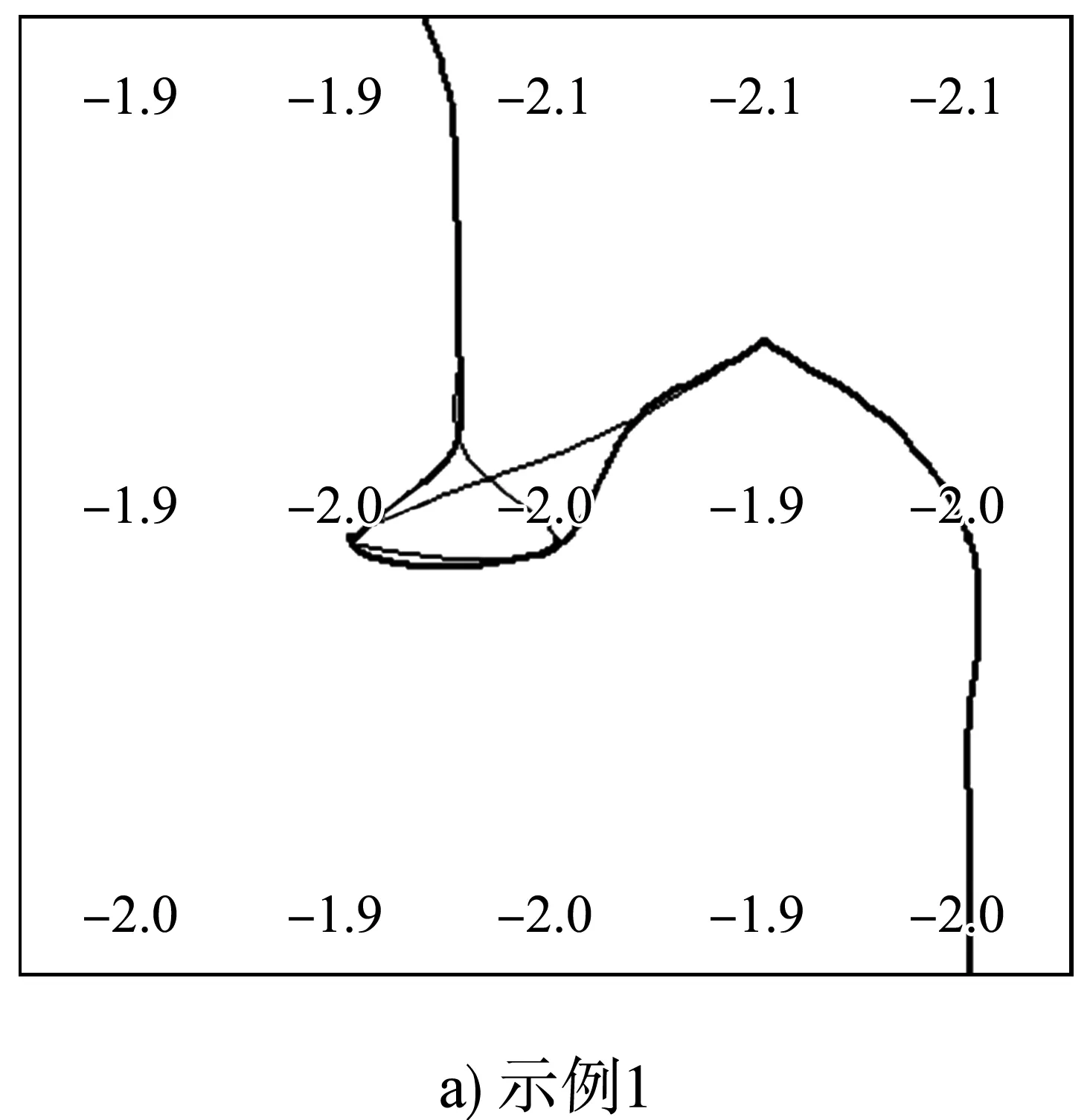
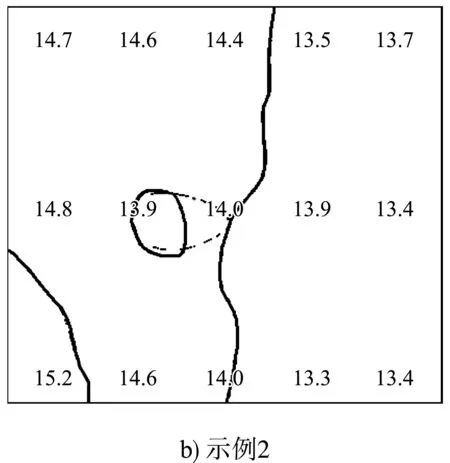
图10 等值线拓扑修正效果

3.5 线形渲染及输出

等值线经过拓扑检查修正，已与测深点的对应关系准确，走向合理，可以输出为CAD图层。输出为CAD前，针对等值线的特征值，进行首曲线与计曲线的区分，并根据内业制图规范赋予不同的颜色和线型。最终利用ArcGIS Engine的ConversionTools工具将图层转换为CAD文件，得到等值线生成的最终成果。经质检人员检查，最终成果不存在拓扑错误。

使用等值线生成平台进行等值线的生成，其流程简化为“导入测量数据——点击‘等值线生成’按钮计算”两步。大幅降低了内业人员的操作难度与工作强度，提升了内业成图效率，可以及时地为电子航道图提供数据，满足电子航道图实时性需求。