随机车流作用下悬浮隧道车-隧耦合振动分析

林 亨， 吴冬雁， 赵俊亮， 项贻强

(1.温州大学 建筑工程学院，浙江 温州 325035; 2.浙江大学 建筑工程学院，杭州 310058)

作为未来深海水域的跨越结构物，悬浮隧道(submerged floating tunnel, SFT)浸没在水下一定深度并依靠自身浮力平衡结构后期的运营荷载。虽然封闭的断面形式与传统隧道相似，但是结构设计过程受动力特性控制的特点与大跨桥梁相同。悬浮隧道因其在利用水下空间隐匿路网交通，优化土地资源配置，单位工程造价低等方面表现出的巨大竞争优势，成为未来跨海交通系统重要发展研究的对象。2018年中国科协年会上，悬浮隧道还曾被列为60个重大工程技术难题之一[1]。

移动车辆荷载是悬浮隧道在运营过程中所要面对的重要动载荷。Tariverdilo等[2]考虑移动荷载作用下的附加质量力对悬浮隧道的动力特性的影响，为研究水下悬浮隧道车-隧耦合振动奠定了基础。基于振动响应的动力放大系数，项贻强等[3]对水下悬浮隧道在移动荷载作用下的参数进行分析。Lin等[4-5]通过弹簧质量块改进车辆模型，探讨水流环境中涡激作用下悬浮隧道流-车-隧耦合振动影响参数。此外，董满生等[6-8]还分析悬浮隧道在不同边界条件下受移动荷载作用的动力响应特性。虽然这些模型一定程度上能够揭示悬浮隧道车-隧耦合振动原理，但在分析过程中移动荷载通常是以一种明确的形式作用在结构上，忽略了不同车辆行驶过程中的差异，将与实际运营情况出现偏差。

近些年来，Calcada等[9-10]从真实的交通情况出发，引入随机车流荷载模型进行车-桥耦合振动研究分析，所得的结论对桥梁结构运营和维护有着重要的意义。殷新锋等[11]根据结构的影响面函数，分析得到随机车流作用下桥梁结构的冲击系数用于结构动力分析，取得较好的实际应用效果。基于此，借鉴车-桥耦合振动的研究发展理论，考虑不同车型、车间距和车速情况下的随机车流模型，对悬浮隧道在随机车流荷载作用下的耦合振动响应进行研究。

1 悬浮隧道结构模型

1.1 模型简化

根据结构概念设计，悬浮隧道通常可以划分为预制拼接隧道管体、对称布置张拉锚索和锚固基础、以及衔接水域两岸驳岸段等几部分，其中隧道管体的直径为D，壁厚为H，张拉锚索沿着管体长度方向(X-轴)分布间隔hi(i=1, 2, …,N)进行布置，整个结构体系如图1所示。在一般静水环境中，由于张拉锚索始终处于张紧状态，故其水平向分力可以自平衡相互抵消[12]，而为悬浮隧道管体结构提供一定的竖向刚度Ki(i=1, 2, …,N)。与此同时，不同状态车辆流在隧道管体内通行并致使悬浮隧道发生耦合振动。

图1 随机车流作用悬浮隧道结构示意图

基于此，简化悬浮隧道模型结构如下：整个隧道管体置于静水环境中，受到张拉锚索竖向约束力的作用；将悬浮隧道管体结构视为等截面等刚度的Euler-Bernoulli梁，且近似考虑结构边界为简支约束；不同状态车辆流在隧道管体内满足随机分布规律，且在行驶过程中不受物理空间上的制约。

1.2 车-隧耦合振动

悬浮隧道结构的外力荷载主要包括流体作用力和移动车辆的接触力。在工程应用中，通常采用Morison方程计算作用在圆柱形结构上的流体作用力fD(x,t)，即计算公式为

(1)

不同车辆类型可简化为不同自由度系列的弹簧-质量块模型，假定车辆在隧道内行驶过程中不与路面发生脱离。可通过三阶Hermit插值函数矩阵N将流体作用力fD(t)和移动车辆作用fv(ξ,t)等效为单元节点力

N1(ξ)=1-3ξ2+2ξ3，N2(ξ)=(ξ-2ξ2+ξ3)l,

N3(ξ)=3ξ2-2ξ3，N4(ξ)=(-ξ2+ξ3)l

(2)

式中:l为单元的长度；ξ为相对单元起始位置的自变量。三阶Hermit插值形函数能够保证相邻单元在边界上的连续性。图2给出了典型i-j梁单元在t和t+Δt时刻的受力变形图。

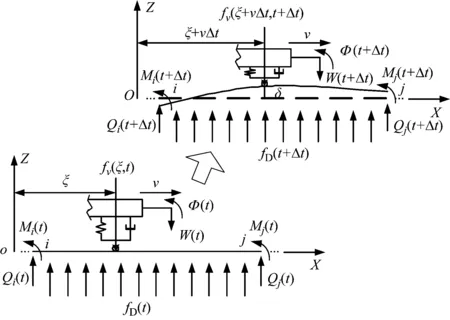
图2 典型i-j梁单元受力分析

1.3 系统振动方程

悬浮隧道车-隧系统通过车辆与隧道之间的位移协调条件及力学条件实现耦合振动，其运动方程可以分离写成两个子系统，表达式可表示为

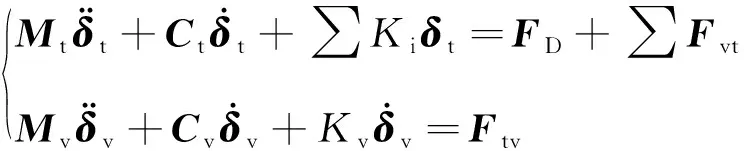
(3)

式中,Mt、Mv分别为悬浮隧道及车辆系统的质量矩阵;Ct、Cv分别为悬浮隧道及车辆系统的阻尼矩阵;Ki、Kv分别为悬浮隧道锚索提供的竖向刚度和车辆系统的劲度系数;δt、δv分别为悬浮隧道与车辆系统的位移向量;Fvt、Ftv分别为作用在悬浮隧道上的车辆荷载和悬浮速调对车辆系统的作用力矩阵;FD为静水环境对悬浮隧道的流体作用力的矩阵。

此外，流体作用力矩阵和耦合力矩阵可分别通过结构单元上的流体作用力和车辆作用力累加得到

(4)

式中:FDe为单元所受的流体作用力。而车辆系统的耦合作用力Fve需根据车轮的前后轴位置(i=1,2,…)并由插值函数进行等效代换得到

(5)

式中:、Φ分别为车辆的竖向位移和转动角度;v为车辆的行驶速度;dv为车轴间距; 流体作用力和车辆作用力与结构和车辆的动力响应有关，在计算过程中需要不断更新外力矩阵进行动力方程的数值求解。

2 随机车流理论

2.1 理论模型

对于道路上行驶车辆而言，有诸多因素会对随机车流的形成产生影响。王达等[14]通过对比实测数据发现，通行的车型、车速和车间距等随机车流参数离散程度明显，通过概率分布函数来定量模拟随机车流。

2.1.1 车型分析

实际车流中的车辆种类及模型较为复杂，将车流大致地分为重型车(H)、中型车(M)、一般小型车(S)三类进行分析。重货车与中型车采用双轴车辆模型考虑车身转动的影响，而一般小型车以单轴车形式直接作用在隧道结构上。基于车流量调查研究[15]，不同车辆类型在车道上服从均匀分布，这里设定三类车型H、M和S的车流量占比分别为10%、10%和80%。不同类型车辆基本参数如表1所示。

表1 不同类型车辆基本参数

2.1.2 车速分析

国内外的学者通过对不同道路(诸如高速公路、城市快速路及城市干道等)环境下不同车型的车速概率分布进行研究，正态分布在实测统计中得到了广泛的应用。在确定车道的车流量后，可根据车速-流量BPR模型对各车型的车速进行模拟

(6)

式中，μvH、μvM和μvS分别代表重、中和小型车的在车道流量为q情况下的车速均值, km/h。不同车型车速的标准差σ通过变异系数υv得到，σ=υv×μ。此外，Leong和McLean通过实测发现畅行车速的变异系数在0.11～0.18[16]，故本文取0.15作为各个车型车速的变异系数进行研究分析。

2.1.3 车间距

车间距直接关系隧道内行驶的车辆数，是随机车流模拟中重要的参数。基于统计的研究结果，采用伽马分布来模拟不同车流量情况下的车间距情况。其基本表达式为

(7)

式中:α为形状参数；λ=1/β，β为尺度参数。吴冬雁在总结相关文献基础上给出参考，当车流量在600～700辆/h范围，α=6.43，β=0.838；而当车流量在1 100～1 200辆/h范围，α=7.295，β=0.406。

2.2 随机车流模拟

基于MATLAB软件操作平台，采用蒙特卡洛法模拟生成系列随机车流荷载样本。先确定随机车流荷载样本数，并结合车流量确定通过悬浮隧道的车辆总数；再根据随机车流车辆类型、车速和车间距的随机函数，计算得到每个荷载样本下各不同车辆的行驶参数；最后形成随机车流荷载样本，并对受荷载结构进行随机振动分析。

图3(a)和(b)给出不同车流量情况下随机车流荷载的样本情况。结合式(6)可知，对车流量低的情况，小型车车流平均速度为57.55 km/h，其高于中、重型车流；而在车流量较高时，重型车车流平均速度为35.83 km/h，比小型车车流平均速度要高7.33 km/h。此外，不同车型的车辆位置和车间距服从相关的随机分布。

(a) 车流量q=600辆/h

3 数值计算方法及算例

为分析悬浮隧道在随机车流作用下的动力响应，本文参考中意合作在千岛湖悬浮隧道方案设计方案参数进行分析[17-18]，取5节相同的100 m隧道节段进行结构拼接，由对称锚索提供竖向支承刚度，具体参数如表2所示。根据本文提出的有限元计算方法和随机车流模拟程序，在MATLAB软件平台上进行数值求解。

表2 悬浮隧道基本参数取值

根据本文提出的理论方法，对随机车-隧耦合系统进行数值分析，整个程序编制的计算流程如图4所示。根据实测所建立的随机车流模型，考虑车型、车间距和车速随机分布的特点，通过蒙特卡洛法生成150个随机车流荷载样本用于系统耦合振动分析。对于水下悬浮隧道结构，通过位移协调和耦合力实现车-隧耦合作用，通过Newmark-β法对系统的耦合振动方程进行数值求解。最后，根据计算的结果进行随机车流作用下悬浮隧道车-隧耦合振动响应进行统计分析。

图4 车-隧耦合程序计算流程图

4 计算结果分析

4.1 随机车流的影响

为了解车辆通过悬浮隧道的振动特性，对随机车流作用下结构加速度时程进行分析。图5给出不同车流量下L/4跨和L/2位置的加速度时程曲线。在不同车流量随机车流荷载作用下，悬浮隧道结构振动情况有所不同。通过分析0～100 s时间段内的加速度响应可知，车流量q=600辆/h在L/4和L/2的加速度均方值arms分别为0.029 8 m/s2和0.037 9 m/s2，其要比车流辆q=1 200辆/h的加速度均方值0.058 9 m/s2和0.065 0 m/s2要小，这说明较高车流量将致使悬浮隧道更为剧烈的振动。

(a) L/2跨位置

在此基础上，对悬浮隧道跨中位置加速度响应进行离散Morlet小波变换。图6给出不同车流量情况下跨中时频变化结果。基于项贻强等估算悬浮隧道振动固有频率的计算公式

(8)

于此同时，进一步探讨悬浮隧道在随机车流作用影响下的结构振动特性。采用瑞利分布、正态分布和威布尔分布对不同车流量随机车流荷载作用下的L/2和L/4位置加速度均方值arms进行拟合。图7为结构加速度概率分布拟合的效果示意图。分析表明，采用正态分布拟合加速度均方值arms的效果最好，瑞利分布效果次之，而威布尔分布的效果不是很好。

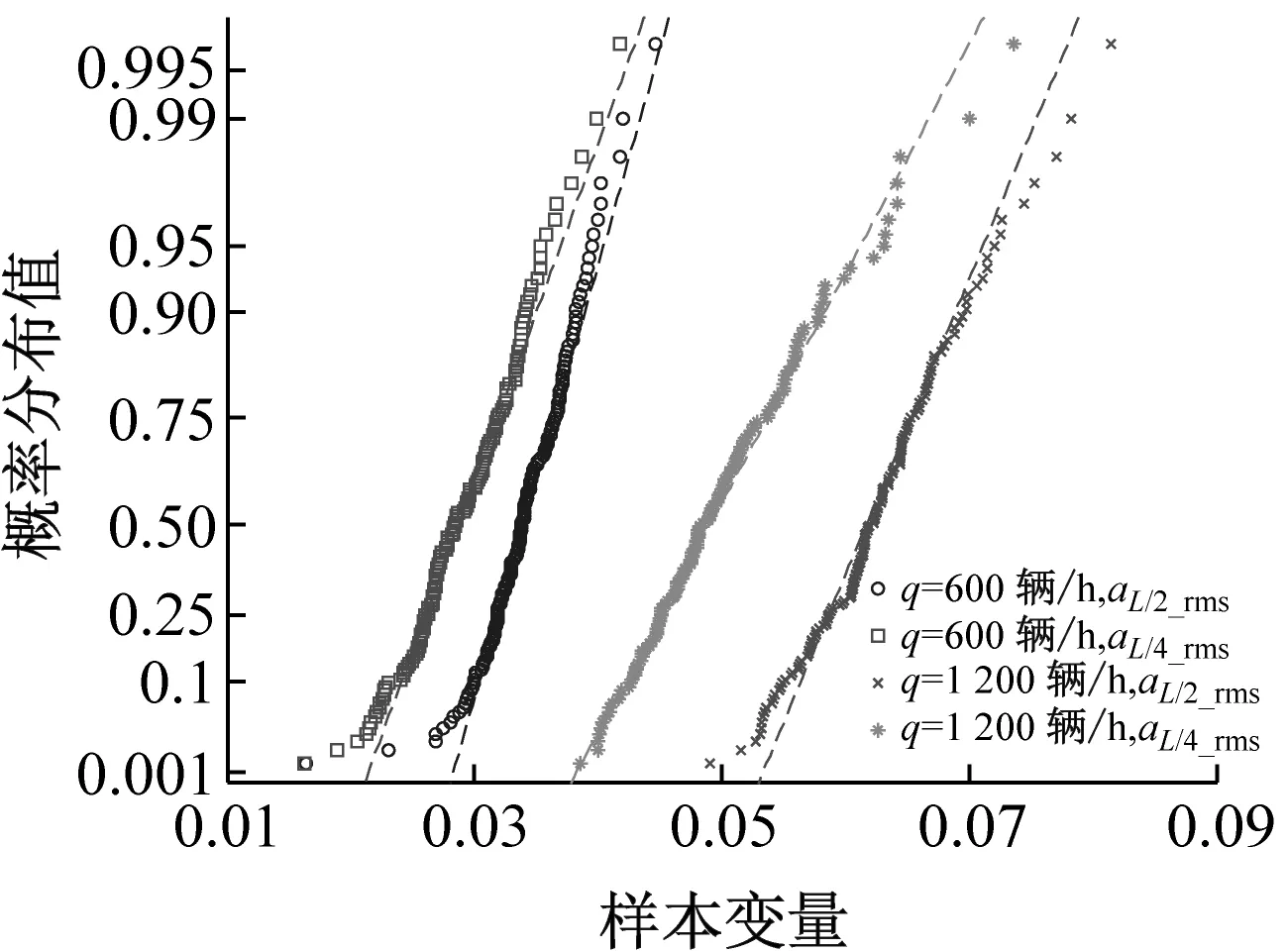
(a) 瑞利分布拟合效果图

4.2 结构参数的影响

悬浮隧道锚索是结构重要的支撑构件，不同的断面尺寸、材料属性和布置形式都会对结构支撑刚度产生重要的影响。为此，通过提高竖向锚索的支撑刚度和改变锚索的布置间距来分析随机车流作用下的悬浮隧道车-隧耦合振动特性。基于车流量q=600辆/h的交通流量，图8给出不同锚索布置的悬浮隧道在车流作用下L/2和L/4的加速度均方值arms的统计结果。

图8 不同锚索刚度悬浮隧道的随机振动特性

总体上来讲，通过分析正态分布概率密度曲线(PDF)和累积概率曲线(CDF)可知，改变锚索竖向支撑刚度和布置间距，其加速度均方值arms仍能够较好的服从正态分布。同时，结构的L/4位置的加速度均方值arms要比L/2位置的要小，这表明L/2位置振动的幅值和剧烈程度要比L/4跨更为激烈。对比图8(a)和(b)发现，提高锚索的竖向支撑刚度，隧道管体的加速度均方值的统计均值μa,rms有所提高，且均方值σa,rms有所增加，这对于结构的稳定是不利的；而不同的是，增大锚索的布置间距，其加速度均值μa,rms和均方值σa,rms有所降低。这说明，增大锚索布置间距，能够控制结构的加速度振幅在相对均衡的水平。

为进一步说明锚索刚度对悬浮隧道的影响，结合拟合得到的悬浮隧道加速度均方值正态分布曲线，选取结构响应的95%分位点作为代表值进行分析说明，结果如图9所示。将不同锚索竖向刚度和布置间距简化为等效锚索刚度k=K/H，随着等效锚索刚度k1=1.19×106N/m降低到3.96×105N/m，隧道管体竖向的加速度均方值呈下降的效果，并且该影响呈现边际效应递减的趋势。这说明，通过控制等效锚索刚度降低结构的振动对竖向支撑刚度大的结构体系明显，而对于结构支撑柔度较大的隧道结构效果较弱。

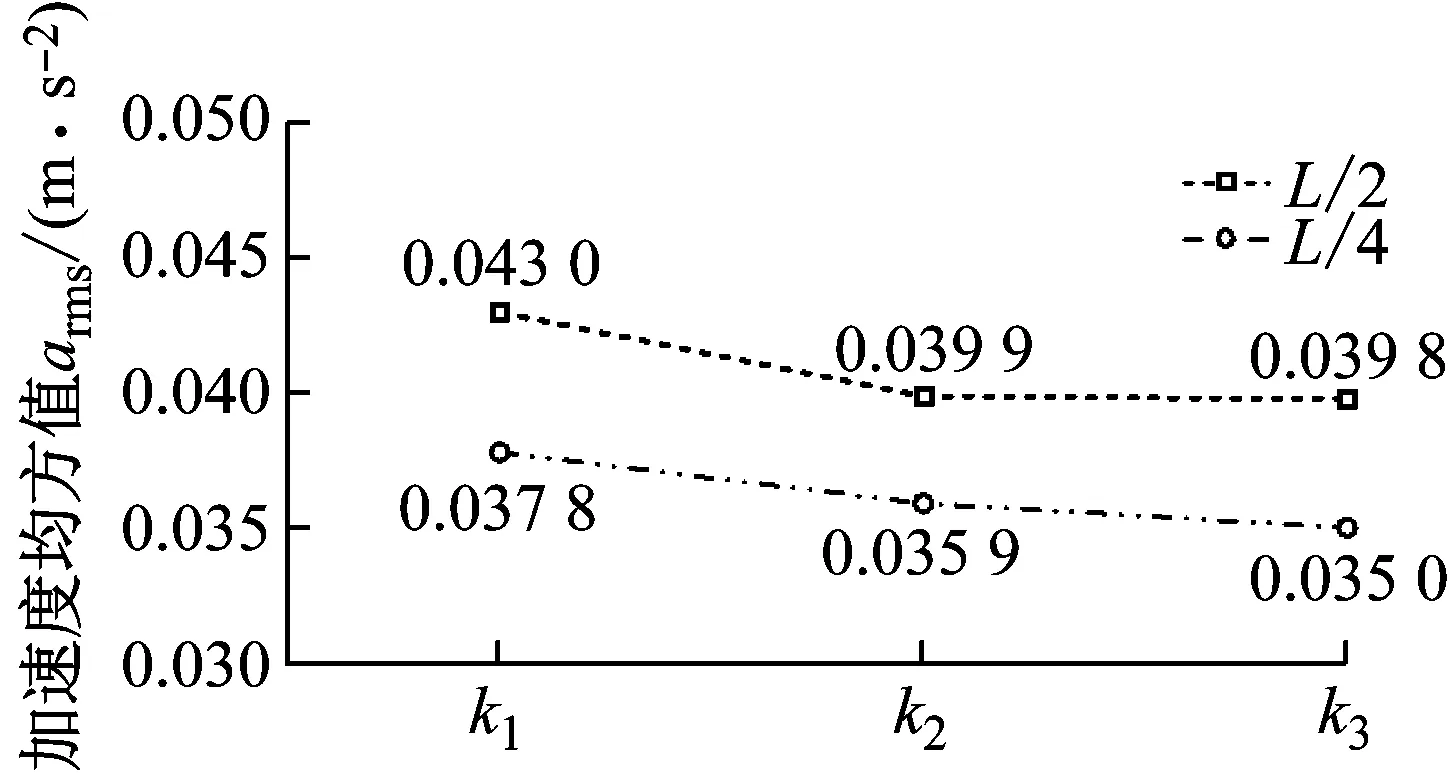
图9 不同等效锚索刚度悬浮隧道95%分位点加速度均方值

5 结 论

本文开展对悬浮隧道在随机车流荷载作用下的车-隧耦合振动进行研究。基于不同车型、车间距和车速情况下的随机车流模型，分别通过蒙特卡洛法和有限单元法进行随机车流和悬浮隧道的数值建模求解，结合统计分布的方法讨论了悬浮隧道的随机振动特性。从中可以得到以下结论：

(1) 悬浮隧道在随机车流作用下发生车-隧耦合振动。对比发现，较高车流量的作用将诱导悬浮隧道更产生更加剧烈的耦合振动。

(2) 在不同随机车流作用下，悬浮隧道的L/4和L/2位置的加速度均方值arms服从正态分布的概率分布形式，且L/2位置受到更明显的随机车流荷载作用影响。

(3) 提高锚索竖向刚度，不利于结构的振动稳定，而增加锚索布置间距能够控制结构的加速度振幅在相对均衡的水平。改变等效锚索刚度来降低结构振动对竖向支撑刚度大的结构体系明显，而对于结构支撑柔度较大的隧道结构效果较弱。

文中仅基于理论数值模型探讨了悬浮隧道在随机车流荷载作用下的振动特性，且对于横向波流等联合作用下的悬浮隧道耦合振动有待进一步的研究。