“互联网+”高中数学几何探究性实验教学的实践与研究

李玉玲?李红庆

【摘要】高中数学几何探究性实验教学既包括狭隘意义下立体几何、解析几何，也包括函数的图像、解三角形测量问题，还包括向量几何问题。几何探究性实验教学既可以是传统意义下的实物操作实验，也可以是应用信息技术展示动态的实验。

【关键词】几何探究性;实验教学;实践与研究

从广义来讲，高中几何教学涉及高中数学的方方面面，既包括狭隘意义的立体几何、解析几何，也包括广义意义的函数的图像、解三角形的测量问题，还包括充当代数与几何桥梁的向量几何。几何探究性实验教学既可以选择购置几何模型或动员学生自做几何模型进行动态演示，也可以应用沙盘、塑泥手工作业来动手演示，还可以借助信息技术进行探究性实验。在“互联网+”环境下，上述几何探究性教学实验都可以云计算和在网络画板上完成，保持了探究性实验的原汁原味，也可以直观演示和记录动态轨迹。现谈一谈在网络画板环境下高中数学几何探究性实验教学的一些实践与研究。

一、立体几何探究性实验教学的实践与研究举隅

1.立体几何探究性实验教学。立体几何探究性实验教学选取问题常常具备3个特征：不具备条件完备性、结论的不确定性和思维过程的发散性。设计这类问题要从构建背景新颖、思辨性灵活和体现核心素养等方面考量，进而培育学生的创新与探究意识。

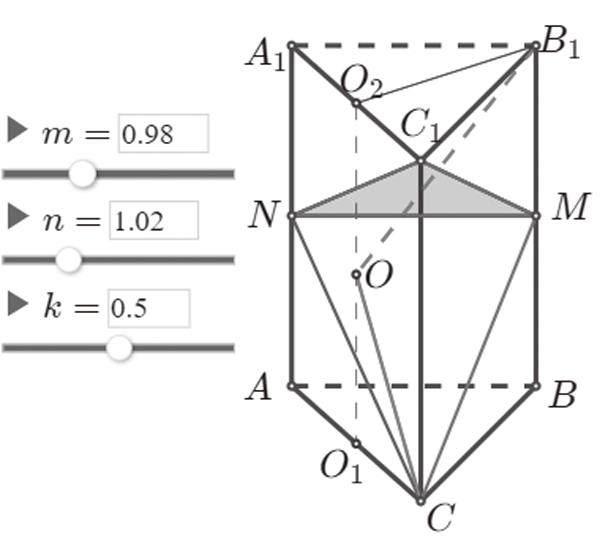
例：如图1，在直三棱柱ABC-A1B1C1中，底面三角形ABC是直角三角形，其中AB⊥BC，AB=3m，BC=4m，CC1=4n，M、N分别BB1和AA1的中点。

（1）探究：CN⊥平面CMN在什么条件下成立;

（2）当点O在平面C1A上移动时，求点O在何处，且λ=m：n为何值时球O是直三棱柱ABC-A1B1C1的外接球。

探究性实验：①通过网络画板计算功能，分别计算CN、CN1、CC1的长度，检验是否满足NC2+CN2=CC12，由勾股定理的逆定理来判断CN⊥NC1是否成立，同样检验CN⊥NM是否成立。

②根据外接球的性质，过△ABC的外心O1，作底面ABC的垂线O1O2，球心O在此直线上，拖动点O，发现当点O是O1O2的中点时，且λ是任意正数。

探究性实验必须与课堂教学实际情境以及学科素养相融合，尽量把探究性实验定位在“辅助性”教学位置上，让学生能运用到纸质环境下的思考与操作。

2.立体几何折叠探究性实验教学。立体几何探究性实验教学也经常选取折叠问题，它包含了数学建模、逻辑推理和直观想象等数学核心素养，通过探究性实验，让学生亲自参与体验折叠问题中平面图形的不变量、不变位置关系，空间图形中出现变化量与变化位置关系，培育学生的空间想象能力与创新意识。

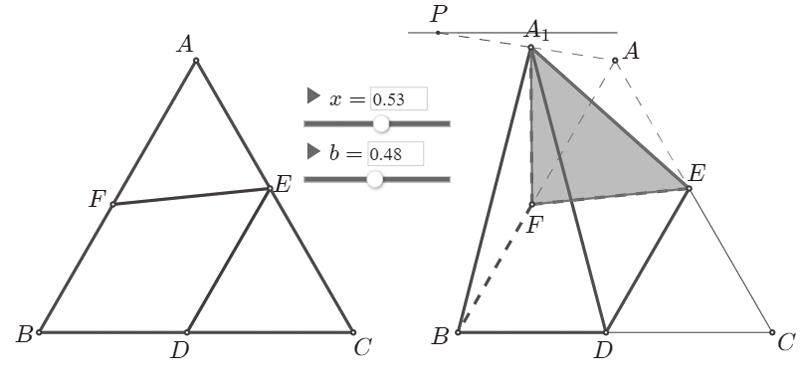
例：在正三角形△ABC中，E、F、D分别CA、AB、BC上的点，设，，，且O﹤χ﹤1（如图2），将△AEF沿EF折起到△A1EF的位置，使二面角A1-EF-B的大小为θ（O﹤θ﹤π），连结A1D，A1D（如图3）。

（1）判断χ取什么值时，A1F⊥平面BED;

（2）拖动χ的值，观察二面角B-A1D-F的随χ的变化规律。

探究性实验：①先拖动平面A1EF，使得θ=90o，再拖动χ观察图形的变化，發现当χ=1/3左右时，EF⊥AB，此时，易知A1F⊥FE，A1F⊥BF，从而得到结果。

②拖动χ观察二面角B-A1D-F的大小随着χ的变大而变小，当χ→1时，二面角B-A1D-F的大小趋近于0。

探究性实验教学的主要目的是培养学生动手实际操作与真实感受立体几何中的点、线、面的位置关系，教学重点不是解决具体的计算问题，而是亲历体验几何图形。基于这种想法，还把点A1设置在线段AP间移动，由拖动b和点P来演示变式情形下探究性实验教学。

二、解析几何探究性实验教学的实践与研究举隅

1.解析几何探究性实验教学。解析几何中探究性实验教学选取问题常常具备4个特征：条件开放、结论不确定性、图形难画和涉及平面几何性质难找。同时也考查学生数学运算、逻辑推理和直观想象等核心素养，特别是数学运算还须具备灵活运算手段与方法的选择优化。

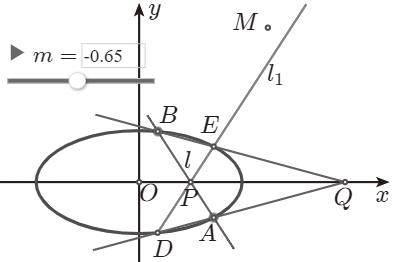
例：如图4，已知椭圆C：χ2/4+y2=1，设直线经过点P（1，0）、Q（4，0），与C相交于两点A（χ1，y1），B（χ2，y2），直线AQ与C另一交点D（χ3，y3），直线BQ与C另一交点E（χ4，y4），若直线DE经过点M（2.5，3），求的方程。

探究性实验：拖动变量m，观察发现直线与DE是倾斜角互补，即斜率是相反数，当然这个发现需要通过运算来检验。但可以先设直线DE的方程为χ=-my+t，最后来验证直线的方程是χ=my+1。再拖动变量m，当直线DE经过点M时，估计的值m为-0.5。这个实验的验证应选择适当算法才能简捷解决，否则运算相当复杂。

算法梳理：第一步，联立方程χ=-my+t和χ2+4y2=4，消去χ，得到关于y的二次方程，根据韦达定理，得到两根和、积关系式;第二步，由Q和D两点得到直线QD的方程，与C的方程联立，得到点A的坐标，同理得到点B的坐标;第三步，根据点A、P、B三点共线，得到直线的方程为χ=my+1，也得到t=1;第四步，将点M的坐标代入方程χ=-my+1，得m=-0.5。

2.解析几何精准画图探究性实验教学。图形难画、问题难想也是解析几何探究性实验教学需要着重考虑的问题，有些问题看似好理解，真正透彻讲清晰也是很难的。如果借助网络画板进行探究性实验教学，那么这样的问题就能迎刃而解。

例：（深圳市2022调研试题11题）已知圆A的半径为1，圆心A到定直线的距离为d，动圆C与圆A和直线都相切，圆心C的轨迹为如图5所示的两条抛物线，记这两条抛物线的焦点到对应准线的距离分别为p1、p2，则。

探究性实验：考虑圆C1与圆A外切情形时，点C1到点A的距离为r1+1，其准线为χ=-1;考虑圆C2与圆A内切情形时，点C1到点A的距离为r2-1，其准线为χ=1，实验结果可以由图6清晰呈现。

先拖动点C1，圆C1总是与圆A内切，与直线相切，点C1形成轨迹是外围抛物线;再拖动点C2，圆C2总是与圆A外切，与直线相切，点C2形成轨迹是里面抛物线。

运用代数运算及变换解决椭圆、双曲线的离心率问题是通常的方法，但在解客观题中把条件转化成平面几何问题，利用平面几何的性质进行求解就会起到四两拨千斤的作用，简捷、直观、清晰地得到结论。

例：过双曲线C：χ2/a2-y2/b2=1（a﹥0，b﹥0）的右顶点A作斜率为-1的直线与两条渐近线的交点分别为B，D，若，则C的离心率为。

探究性实验：根据平面几何性质，当时，则yD：yB=3：1，边拖动变量，边观察yD：yB的比值变化，当其比值接近3时，此时就得到了的近似值（见图7）。

网络画板是张景中院士的研究团队为几何探究性教学量身打造互动交流平台，在立体、解析几何上非常好用，只要用心思考也可以用在代数、三角函数、向量几何等模块中。

三、向量几何探究性实验教学中的实践与研究举隅

1.用向量探究平面幾何问题实验教学。向量几何在数学中起到联系代数与几何的桥梁作用，属于数学工具性内容。它能简捷表示点、线、面的位置关系，又有代数运算的功能。因此，以向量几何为背景的探究性实验教学更需要实践与研究。

例：在△ABC中，有，，

，其中是区间（0，1）的变量，设△ABC的重心为G，△DEF的重心为G1，拖动观察点G与点G1的位置关系，给出结论与算法分析。

探究性实验：如图8所示，在平面内取一点P，作，，拖动变量，观察向量和的变化，发现向量纹丝不动，说明了两个三角形的重心重合。

算法分析：第一步，根据向量线性运算，算出以，为基底的向量，于是得;第二步，分别算出以，为基底的向量，，根据三角形重心的向量公式，得;第三步，再由，发现两个向量表达式一样，从而证明了两个三角形重心重合。

2.用平面几何探究向量问题实验教学。向量几何具有工具性，用向量解决平面几何、三角函数、解析几何的问题比较直观、简捷。但向量表示三角形的四心，除了三角形的重心可借用向量的基本定理，由线性表示外，其他的外心、内心、垂心用向量的基本定理表示还是比较困难的，对比可以借用平面几何的性质和正余弦定理结合向量的基本定理进行表示。

例：已知I、O、H分别为△ABC的内心、外心、垂心，记BC=a，CA=b，AB=c，探究怎样以、为基底，分别表示、、。

探究性实验：如图9（a），拖动顶点C观察向量、的变化，分别计算线段AB1，AB的长度，计算它们比值，再计算b与（a+b+c）的比值，发现两个比值完全一样，启发解题的寻找方向。

解法分析：根据探究性实验给予解题方向，借用平面几何中三角形内角平分线成比例定理，应用好比例性质，就得到结果，详细解答见文。

探究性实验：如图9（c）所示，拖动点C和P，发现线段CH长度总是OM长度的2倍，就需要作辅助线构造平行四边形OMNK，这样就能找到AC1与AC的比值了，即得到的表达式。如图9（c）所示，根据欧拉定理，由，即可得到的表达式。

四、其他几何探究性实验教学的实践与研究举隅

1.导数几何探究性实验教学。应用导数研究函数性质的大量试题中需要求参量的取值范围，这类试题由于选择是超越函数，函数图像形状复杂，关键的极值、间断点、最值点难求。虽然应用导数的确可以描述函数图像的大致走势，但实际计算过程也相当复杂。因此，通过网络画板进行探究性演示实验教学可以帮助学生从根本上理解函数图像，理解应用导数研究函数的意义。

例：已知函数?（χ）=（χ+1）-mχ（1-χ）-1对于任意的x∈（0，1），恒有?（x）﹥1，求实数m的取值范围。

探究性实验：如图10所示，拖动变量m时，由小到2时，观察函数在区间（0，1）内图像，函数值均大于1;当拖动变量m时，由2到无穷值时，观察函数在区间（0，1）内的图像，图像变得很复杂，总有小于1的情形。有时也可以通过演示实验发现实验结束与纯理论计算结果不吻合，探究性实验不仅有辅助教学作用，其实几何探究性实验还有检验性作用。

2.三角函数几何探究性实验教学。三角函数具有函数的共性，但也有自身的个性，尤其是刚接触弧度制时，学生不理解开始时弧度制的角是绕着原点旋转而成，作图像时又是以x轴为角。建立弧度制就要让角由实数表示，严格意义上讲弧度本身是没有单位，它的含义是弧长长度与半径长的比值，这个比值就是没有单位，相对于角度制的度，就建立了弧度制的弧度。在三角函数中，几何探究性实验的重点在于探究弧度与函数图像的关系。

例：设计一个模型，能帮助初学者理解弧度制的三角函数图像。

探究性实验：如图11所示，以Hz为轴作底面半径为1的圆柱侧面，在圆柱侧面绕一个螺旋曲线，把这条曲线压缩到底面，就形成了弧度制为单位的角。再设一条y轴，曲线在y轴的投影就是对应的函数值，把曲线拉长放在x轴上就成了以弧度为单位的横轴了。做成实物模型，教师注意诱导分析，学生就能理解以弧度制为单位的三角函数图像。

3.不等式几何探究性实验教学。启发于教材关于两个正数的均值不等式的模型构造（图12 a），在探究性实验教学中设计了三个正数的均值不等式模型（图12b），先拖动m与n的值，让学生观察EG、GF、EF的长度有什么规律？在什么情形下能使EF=EG+GF。此时，发现m与n有什么关系？然后让学生拖动a、b、c的值，把得到结论分享给同学。

几何探究性实验教学重点是理解事物的几何形态的位置关系，培育学生的直观想象能力与意识，使其借助图形语言理解数学的抽象性。当然探究性实验只是一种教学辅助工具，真正要把数学学好还需要学生具备熟练的运算能力和严谨的思维。

【参考文献】

[1]李红庆.跟我学解高中数学题（第2版）[M].哈尔滨：哈尔滨工业大学出版社，2021.

（基金项目：本文系教育部全国规划课题“互联网+高中数学几何探究性教学的实践与研究”的研究成果，课题编号：FHB180557）