数字双闭环控制下全桥同步整流电路建模及环路设计

郑 堃, 宋 超, 刘 松

(中国电子科技集团公司 第二十四研究所, 重庆 400060)

0 引 言

随着电力电子变换器朝小型化、轻量化、智能化趋势发展,数字信号控制器(Digital Signal Controller,DSC)在开关电源中的应用愈加广泛。DSC除通信、时序算法控制等,在开关电源中起的核心功能之一便是主导电路的环路计算。数字控制中环路计算所固有的采样环节、一拍延迟环节、零阶保持器环节[1]使得其较之传统的模拟控制有着显著区别。同时,全桥同步整流电路以其拓扑结构简单、功率大、效率高等优点在开关电源工业界大受青睐。因此,研究数字控制下全桥同步整流的电路建模与环路参数设计具有重要的工程指导意义。

本文首先针对数字双闭环控制下全桥同步整流电路进行了建模分析,采用数学近似方法对采样环节、一拍延迟环节、零阶保持器环节进行了等效,然后根据建立的等效模型对外电压环和内电流环参数进行了整定,最后通过仿真和实验验证了建模与参数整定的正确性。

1 模型建立

1.1 电路拓扑

数字双闭环控制下全桥同步整流电路如图1所示。

图1 数字双闭环控制下全桥同步整流电路

数字双闭环控制下全桥同步整流电路主要由两部分组成:全桥主功率拓扑部分和DSC运算部分。

全桥主功率拓扑部分包含输入电源Uin,一次侧开关管VT1～VT4,二次侧开关管VT5～VT8,隔离变压器T1,隔直电容C1,输出低通滤波器L、C。一次侧4个开关管VT1～VT4工作在斩波模式,二次侧4个开关管VT5～VT8工作在同步整流模式。从电感和功率开关管的连接方式来看,主功率拓扑为典型的UKBC型全桥拓扑。主功率拓扑部分的物理量均是模拟的。

DSC运算部分主要包含电压外环控制和电流内环控制两大环节。电压外环起维持输出电压稳定的功能,电流内环则起控制输出电感开关周期平均电流的功能。DSC运算部分具体包括虚拟的采样开关S1、S2、S3、S4,电压环补偿函数Gu(s),电流环补偿函数Gi(s),DSC运算中所特有的零阶保持器和占空比更新延迟、控制脉冲的产生及分配。DSC运算部分的物理量均是数字的。

综上所述,数字双闭环控制下全桥同步整流电路系统为数-模混合控制系统,其建模与传统意义上的模拟控制系统有着显著差异。

1.2 控制框图及传递函数推导

数字双闭环控制下全桥同步整流电路系统控制框图如图2所示。

图2 数字双闭环控制下全桥同步整流电路控制框图

图2中,R代表电路的负载阻抗,kpwm代表电路等效的比例环节,其值等于输入电压经变压器T1后之值与等效载波数字量之比。

Gh(s)为零阶保持器环节,其传递函数为

(1)

Gd(s)为数字占空比量更新延迟环节(考虑当前占空比在下个采样周期更新),其传递函数为

Gd(s)=e-Tsas

(2)

式中:Tsa——DSC的采样时间。

在奈奎斯特(二倍采样)频率范围内,采样开关VT1～VT4等效传递函数Gsample(s)[2]为

(3)

令s=jω,在ωTsa足够小时(系统处于中低频段时)式(1)可化简为

(4)

采样开关、保持器、数字占空比量更新延迟三者乘积为

(5)

由式(5)可得,采样开关、保持器、数字占空比量更新三者乘积可等效1.5拍采样时间延迟。

2 环路整定思路

数字双闭环控制下全桥同步整流电路系统由电流内环、电压外环组成。数字双闭环控制下全桥同步整流电路简化控制框图如图3所示。由图3可知,系统内外环分界明显,设计时可遵循先内环后外环的原则分步设计。

图3 数字双闭环控制下全桥同步整流电路简化控制框图

2.1 电流内环设计思路

电压外环的输出量即为电流内环的给定值,电流内环实现的是对二次侧电感平均电流的有效控制。特别地,对于全桥同比整流拓扑而言,二次侧电感平均电流与负载电流相等,对平均电流的控制即可实现输出电流的控制。由图3可推导,系统电流内环的开环传递函数Gcopenloop(s)为

(6)

由式(6)可得,未补偿前系统电流环的开环传递函数由两个极点、1个零点、1.5拍延迟构成。其中,两个极点构成了典型的振荡环节,其振荡频率与电路LC谐振频率一致;一个零点为RC零点;1.5拍的延迟基准时间为采样时间。

针对系统电流内环传递函数的特性,补偿函数应具有以下特征:

(1)具有两个振荡频率附近的复零点以兑消原系统振荡环节造成的相位与幅值畸变。

(2)存在1个零极点,以消除系统稳态误差

(3)存在1个高频极点,以滤除系统高频噪声,同时与(1)、(2)中零极点组成物理可实现的双极双零点组合。

(4)系统增益适当,使得系统截止频率较不存在延迟的模拟控制系统偏低,从而减小1.5拍延迟环节的影响。

根据上述要求可得,Gi(s)表达式为

(7)

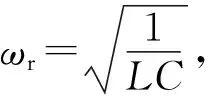
(8)

式中:k1——直流增益;

Q——品质因数;

p0——高频极点。

2.2 电压外环设计思路

一般地,在传统的双闭环控制系统中,在外环建模过程中,由于内环的带宽比外环带宽大,故而在外环建模时,内环可等效为比例环节。但在数字控制系统中,考虑到固有的1.5拍延迟,系统内环不能单纯地被等效为比例环节,应以准确的表达式来指导电压外环的设计,根据图3可得

(9)

由式(9)可得,考虑到电压外环,由于存在1.5拍的延迟环节,整个系统的开环传递函数为非典型的二阶系统,其求解零极点的方程为超越方程,故在工程实际中,宜以伯德图法求解。

3 设计实例

本节将通过实例具体阐述数字双闭环控制下全桥同步整流电路环路设计方法。考虑电路参数:输入电压Uin=200 V,变压器匝比5∶1,等效载波数字量4 096,C=20 μF,R=1.3 Ω,L=3 μH,额定输出电压28 V,采样频率Tsa=125 kHz。

3.1 电流内环整定

根据上述参数,未补偿前电流内环传递函数Bode图如图4所示。其中,延迟环节传递函数利用Pade三阶近似法[3]表征。

由图4可直观得出,未补偿前系统内环存在LC谐振尖峰,谐振频率即为LC谐振频率。同时可以注意到,由于存在延迟环节,不同于一般模拟控制系统,本系统的相位曲线是持续下降的,这个特性贯穿于内外环设计始终。其相位延迟角度可通过式(5)进行估计。

图4 未补偿前的电流内环传递函数Bode图

根据2.1节设计思路设计了电流补偿器,具体取值为p0=7.85×105,k1=1.4×1011,Q=5。

电流补偿器传递函数Bode图如图5所示。

图5 电流补偿器传递函数Bode图

由图5可得,电流补偿器环节类似“陷波器”环节,在特定频率点幅值急剧减少、相位急剧增加,可有效消除原系统电流内环所固有的相位与幅值畸变。

经电流补偿器补偿,补偿后的电流内环传递函数Bode图如图6所示。

由图6可得,补偿后的电流内环传递函数Bode图的振荡环节已被有效消除。低频增益足够大的同时截止频率足够高(30 krad/s,约为5 kHz),能够较好地满足系统要求。

图6 补偿后的电流内环传递函数Bode图

3.2 电压外环整定

电流内环的闭环传递函数与电压环补偿函数之积即为电压控制环路的开环传递函数。未补偿前的电压外环传递函数Bode图如图7所示。

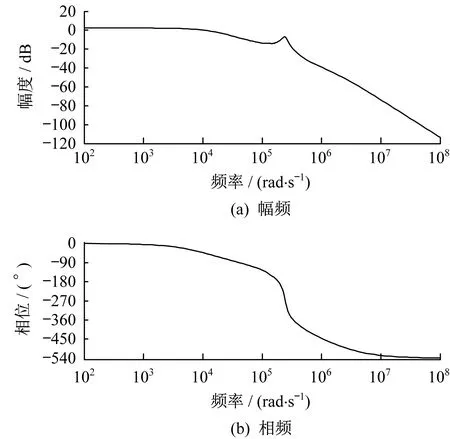
图7 未补偿前的电压外环传递函数Bode图

由图7可知,未经补偿的电压外环传递函数Bode图也存在微弱的谐振尖峰,由于无法直接求解零极点方程以确定谐振频率,故而设计电压补偿器时,应使截止频率较小以尽量避开此谐振尖峰,同时保证相位裕量。可采用工程上易于实现的一零极点+一极点+一零点补偿器形式[4]。其表达式为

(10)

同时前已述及,电流内环的闭环传递函数与未经补偿的电压外环传递函数伯德图一致,则可从侧面印证电流内环设计合理性:即在低频时,系统能够准确跟踪给定值。

本设计实例取k2=1.25×103,z0=1 000,p1=6.28×103,则可绘制出补偿后的电压外Bode图。补偿后的电压外环传递函数Bode图如图8所示。

图8 补偿后的电压外环传递函数Bode图

由图8可知,补偿后电压外环传递函数的截止频率适宜(10 krad/s,约为1.6 kHz,远离系统谐振频率点),相位裕量足够,同时高频段幅度呈现-40 dB/(°)衰减趋势,符合系统要求。

4 实验验证

为了验证建模及环路设计的正确性,研制了一款额定功率560 W,额定输出27 V的样品电路。样机如图9所示。

图9 样机

该样机主电路、环路参数取值如本文4小节所述。值得注意的是,电流环、电压环的控制器s域传递函数需先通过双线性变换法转换z域表达式,然后在DSC中通过差分方程的方式实现。

启动电压与输出电流波形如图10所示。

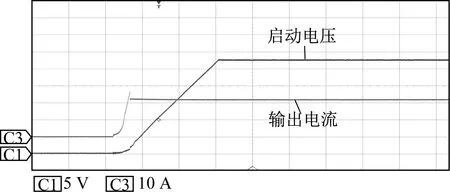
图10 启动电压与输出电流波形

由图10可知,启动时刻,由于电压外环的误差最大,导致经由电压控制器后的电压环输出量最大,从而影响电流环,使得输出电流迅速上升直至达到最大限流保护电流,然后输出电流超调后经控制器调节下降为负载电流大小且保持恒定。由于启动时刻电压外环的给定值是缓慢增加的,因此电路此时达到了动态平衡的状态。

综上,依据本文建模和环路设计思路方法所设计的数字双环全桥同步整流样机电路输出电压、电流波形良好:启动电压平滑无超调,启动电流迅速无电涌,符合工程实际的需求。

5 结 语

推导了数字控制下全桥同步整流电路的电压电流双闭环模型。遵循先电流内环、后电压外环的原则详细讨论了数字控制下全桥同步整流电路环路设计的思路与方法。搭建了一台额定功率为560 W的样机电路,通过实验验证了设计思路正确性。