基于粒子群算法改进极限学习机的风电功率短期预测*

田艳丰, 王 顺, 王 哲, 刘 洋, 邢作霞

(沈阳工业大学 电气工程学院, 辽宁 沈阳 110870)

0 引 言

随着能源和环境的日益严重,迫切寻求一种新的能源供给方式,风力发电技术的成熟为转变能源发展方式注入新的动力;但由于风速的不稳定与风向的变化,使得其供电系统的频率、电压不稳定及风电机组运行存在间歇性等问题,最终导致风电场的输出功率具有高度随机性[1-2]。电网运营商为了能及时高效的调度风电机组,并在风电市场运营上有更好的决策,必须对风力发电功率进行准确的预测[3-5]。

人工智能的迅速崛起,研究者将人工智能算法引入风电功率预测中。包括BP神经网络(BP)、支持向量机(SVM)和ELMAN神经网络等高级算法。文献[6]提出基于时间序列的ARIMA模型对风力发电功率进行短期预测,是一个较简单传统的预测方法,但是对气象信息有较强的依赖性且数据处理较复杂。文献[7-8]巧妙地将小波分解法分别与ELMAN神经网络和极限学习机神经网络相结合,有效的解决了其他算法在训练过程中极易陷入极小值与不稳定的问题。在此过程中分别对分解后的不同频率信号进行预测重构,两种模型较大程度的降低了风电功率的预测误差。但是预测效率较低,计算过程较复杂。文献[9]将模态分解与支持向量机算法相结合进行预测。此方法独特,预测准确度较高,但具有分解与计算较复杂,计算时间较长的缺陷。文献[10]提出了ADQPSO-SVR短期风电功率预测模型。该算法与BPNN和RBFNN等其他方法相比,能够提高短期风电功率预测的精确性。文献[11-12]均提出了预测风电功率的混合模型算法,一个是基于高斯混合模型的RBF神经网络预测模型,另一个是基于ARIMA的卡尔曼滤波的神经网络混合模型算法。在风电功率预测上均能达到预期效果。文献[13-15]分别阐述了交叉熵理论功率预测,支持向量回归(SVR)以及SVM预测的方法。文献[16]介绍了粒子群优化的KELM在特征参数预测上的运用。文献[17]引出极限学习机与核极限学习机的理论,阐明了该算法的特点与优势,并进行严格的论证。

针对以上预测算法中存在的计算复杂、耗时长、波动性强和精确度不高等问题,本文提出一种基于PSO-KELM的风电功率预测模型,通过该模型分别与GA优化的KELM预测模型以及RBFNN,LS-SVM神经网络的风电预测模型进行对比分析,结果表明PSO-KELM预测的效果更加精准,有较高的稳定性,且误差较低,收敛时间较短,大大提高风电功率预测算法的性能。

1 算法的提出

1.1 极限学习机(ELM)

极限学机(Extreme Learning Machine,ELM)神经网络模型与其他方法相比,极限学习机只需设置隐层神经元的数目,通过求解方程β得到唯一的最优解。ELM神经网络模型如图1所示。

图1 ELM神经网络模型

设有N个任意的样本(Xi,ti),其中式Xi=[xi1,xi2,…,xin]T∈Rn,ti=[ti1,ti2,…,tim]T∈Rm对于只有隐藏L节点的神经元网络,其可以用作:

j=1,2…N

(1)

式中:g(x)——激活函数;

ωi=[ωi1,ωi2,…ωin]T——输入层的权重;

βi为——输出层的权重;

bi——第i个隐藏层;

ωi·Xj——ωj和Xj运算的内积。

为了减小神经网络的输出误差,其学习目标函数为

(2)

即存在βi、ωi和bi,使得

j=1,2…N

(3)

上述方程用矩阵简单表示为

Hβ=T

(4)

其中

(5)

式中:H——神经网络隐层的输出矩阵;

β——隐层和输出层之间的权重;

T——神经网络输出的期望向量。

如果隐层神经元数量等于训练集样本的数量,则极限学习机构造成的SLFN与训练样本之间的误差对于任何ω和b几乎为零。并且一旦任意确定隐含层连接权值与隐层神经元的阈值,只需设置隐层神经元的数目便可以得到最优解。连接权值β可由最小二乘方程组求解得到：

min‖Hβ-T‖=0

(6)

传统建模过程中,隐含层节点的数目通常小于训练集的数目,所提取的样本数据极有可能存在复共线性问题。而复共线性问题使得在求解过程中随机矩阵奇异,得到多个隐含层权值,使得输出权值不唯一,对预测结果产生不良影响。

1.2 基于核函数的极限学习机

核极限学习机(KELM)[18]是一种改进的算法,将ELM和核函数相结合,弥补极限学习机的缺陷,避免极限学习机固有的随机性,使得极限学习机的计算更具优势,提高模型的适应性和稳定性。

1.2.1 定义核矩阵

应用Mercer’s条件定义以下核矩阵：

(7)

随机参数矩阵HHT采用核函数Ω替代，在计算复杂度减少的同时，获得了性质更好的高维投影。核函数相关参数设定完成之后，随机矩阵HHT的参数通过计算公式(7)被唯一确定。h(x)为隐层节点输出函数。对于KELM神经网络算法运用RBF高斯核函数即：

(8)

式(8)中,σ为径向参数,μ与v为输入向量。

1.2.2 引入岭回归常数和高斯核函数

采用岭回归理论：将正常数I/C添加到HHT构成单位对角阵的对角线上,巧妙的避免随机矩阵奇异问题,根据广义逆理论,这时对于权值向量可以求得唯一的解。输出权值计算结果为

(9)

式中:I——对角单位矩阵HHT通过核函数的样本映射产生的矩阵;

C——惩罚因子,用于调节结构化风险与经验化风险所占的比重。

ELM训练模式表示为

(10)

(11)

其中,p=1,2,…,N。

LPELM——损失函数;

h(xp)——隐含层的输出函数;

tp——理论真实值;

ξp——误差。

从式(10)可以看出,通过调节惩罚因子C,来对损失函数进行调整,而损失函数是对式(11)中误差ξp的充分反映,也就是通过参数C来调整损失函数,间接调整ELM的误差,使其进行更精准的预测。同时C还有纠正求解过程中的矩阵奇异的问题,从而使得权值唯一确定。对高斯核函数K(x,x)确定后,Ω为唯一值,一旦确定惩罚因子C,就得到输出层的权值。故KELM以核映射的稳定性取代ELM中映射的随机性,克服ELM中由于参数赋值的随机性所引起的模型输出的波动性,更加简单方便,效率更高。

1.3 PSO-KELM寻优

由式(10)可知,惩罚因子C发挥着调整结构风险最小化和经验风险最小化两者互相矛盾占比的作用。核参数σ控制核函数的径向作用范围,充分反映出非线性函数的性态与特点。KELM中采用RBF高斯核函数。所以,参数C与σ的取值对KELM的影响大。粒子群(PSO)算法[19-20]是一个简单高效的寻优算法。利用粒子群(PSO)算法求解KELM的核函数中惩罚因子C与径向参数σ的优化值,建立了基于粒子群优化的核极限学习机模型[21]。

2 采用PSO-KELM算法进行预测

2.1 数据的归一化

风电功率随着风速而变化,而风速由于气候原因,变化极大,所以此类数据就有很大的波动性。为了减少模型的计算时间,采用数据归一化方式处理[22]：

(12)

其中,xmax=max(xi),xmin=min(xi)。

式中:xi——原始数据值;

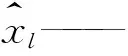
针对核极限学习机参数选择,在参数优化过程中,以MSE作为适应度函数的误差标准,适应度G为

(13)

式中:yj——数据实际值;

G越大,表明这组学习参数相对较差。

2.2 预测与评估

根据行业标准NB/T 10205—2019《风电功率预测技术规定》规定的风电功率预测结果评价标准,采用MAPE、MSE和RMSE[23]作为评价风电功率预测精度的指标。PSO-KELM算法流程如图2所示。

图2 PSO-KELM算法流程

3 实例分析

3.1 数据处理

以东北某风电场某年一个季度数据为实验样本。为了预测的准确性,样本数据每隔15 min采样一次。为了预测精准的同时要满足电力生产要求,将每小时内的4个数据作平均值处理,转化成时间分辨率为1 h的数据。需要对缺失值和异常值进行数据预处理,用均值法填补缺失数据,确保建模数据的完整性和合理性[24]。取其中的7 d数据用于建模预测,前5 d的数据作为训练集,后2 d的数据作为测试样集。

3.2 PSO-KELM算法预测分析

采用PSO-KELM算法,默认次数为20,终止迭代次数为30。PSO的认知系数为5,惯性权重为1,两个加速因子分别为1.6和1.7。

适应度曲线如图3所示。随着进化代数的增加,适应度曲线反映出种群中个体适应度差异性越来越小,适应度曲线趋近于0.0180。

图3 适应度曲线

预测仿真图如图4所示。

图4 预测仿真图

由图4可见,PSO-ELM算法的MAPE为16.478;MSE为6.697 MW;拟合度R2为0.890,适应度为0.0184,拟合效果较好。

3.3 粒子群(PSO)与遗传(GA)优化效果对比分析

由于考虑了算法波动性,每种算法都要执行几次。适应度对比如表1所示。

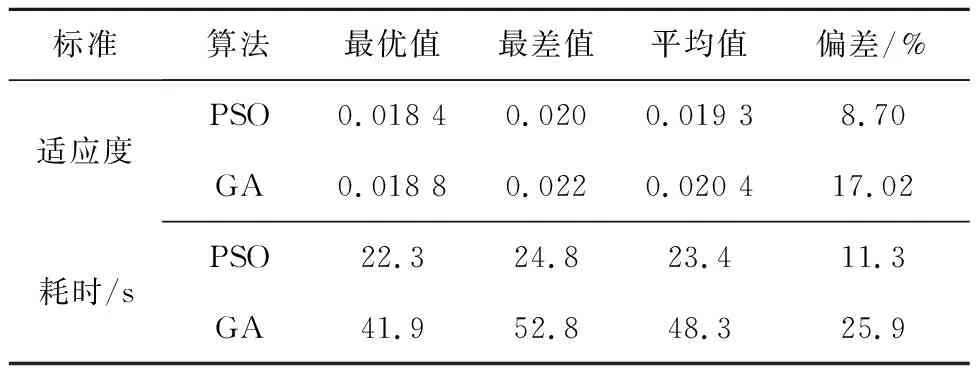
表1 适应度对比

由表1可知,遗传算法GA优化算法所得最优适应度为0.018 8,其30次独立运行中适应度的偏差为17.02%,而PSO算法的误差为8.70%。由此可知PSO算法比与GA算法具有更小的误差。除了适应度以外,对两种优化算法的所耗时长进行对比。对于遗传算法GA所耗时长最短为41.9 s,最长为52.8 s,其与PSO相比时间耗费过长。PSO相比于GA在适应度明显有改进,适应度最优值降低2.12%,而且平均耗时缩短约28 s,节约寻优时间,同时优化效果更好且稳定。PSO优化算法具有全局寻优能力强、鲁棒性好和计算耗时短的优点[25],其优化总体性能强于GA优化算法。因此采用PSO对核极限学习机的两个重要参数(惩罚因子)C与σ(径向参数)进行寻优。

通过30次优化运行,PSO-KELM最优学习参数C为26.047,σ为0.618。GA-KELM最优学习参数C为37.360,σ为0.936 2。

3.4 PSO-KELM和GA-KELM模型预测分析

误差分析如表2所示。

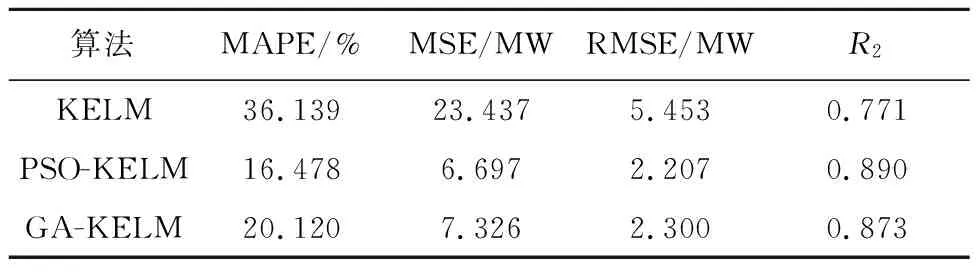
表2 误差分析

由表2可见,PSO-KELM的MAPE为16.478%,与参数非优化的KELM、GA-KELM相比,分别降低19.661%和3.642%;对于PSO-KELM预测的RMSE为2.207MW,在2种模型中也是最低的,拟合度也最高,PSO-KELM的预测效果最佳。

仿真预测模型结果如图5所示。

由图5可见,基于PSO-KELM相对于GA-KELM与KELM的两种风电功率预测模型精度更高,其中非优化的核极限学习机KELM与真实曲线差异性较PSO-KELM与GA-KELM偏大。这主要是因为PSO算法优化KELM中的惩罚因子C及核参数σ,得到最佳的模型参数。

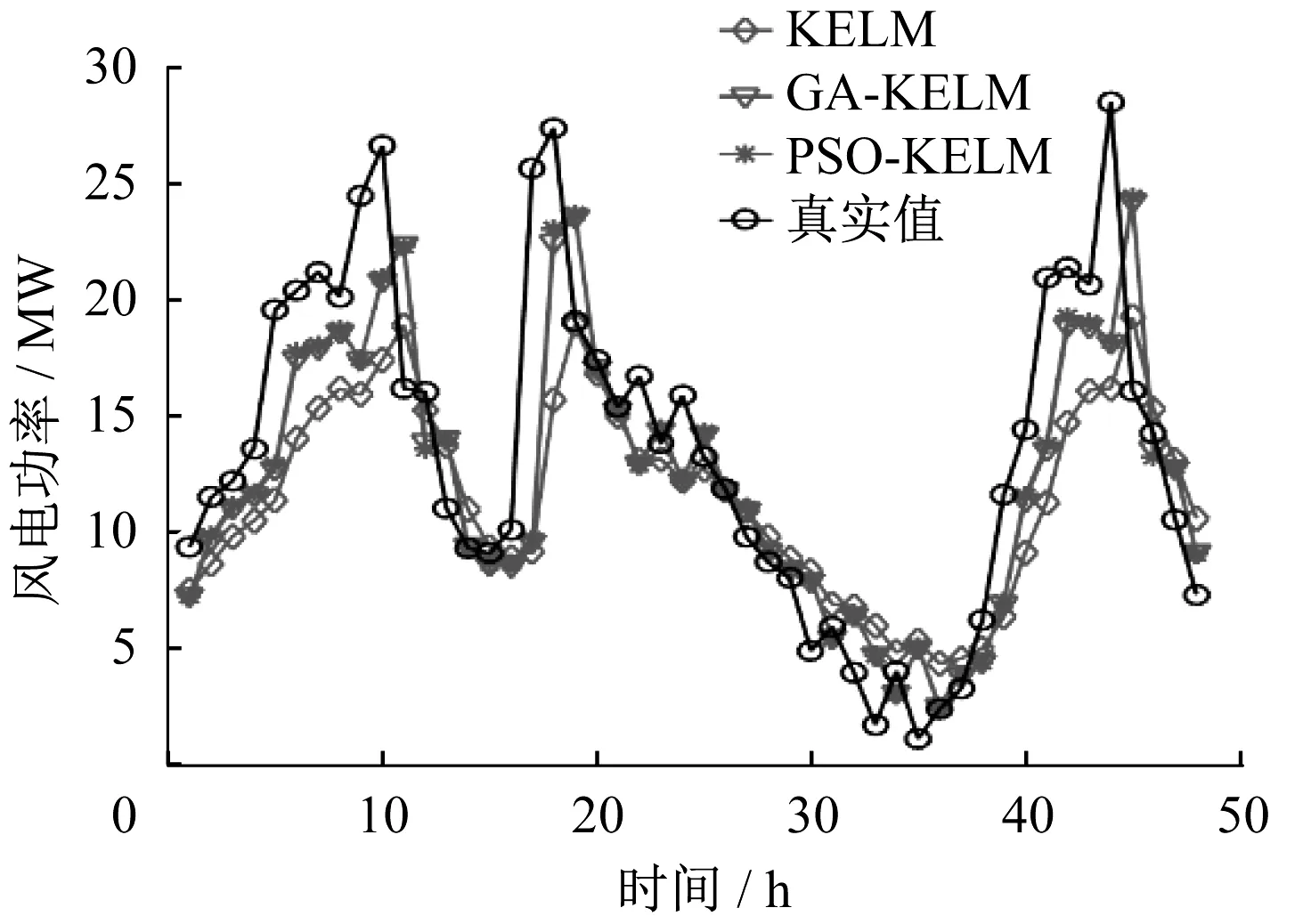
图5 仿真预测模型结果

4 几种不同模型预测效果分析

为了更好地验证PSO-KELM风电功率预测模型的精确性,构建了常用的神经网络预测模型,分别是径向基神经网络模型(RBFNN)和支持向量机神经网络模型(LSSVM),对风电功率进行短期预测。预测的时长范围与先前的相同,模型的评价指标也相同。本文列出单一预测模型和优化模型的误差分析。3种模型误差对比如表3所示。由此可得出,在独立运行30次的粒子群优化的核极限学习机中,其RMSE较RBFNN、LSSVM和GA-KELM的均方根误差分别减少了2.465 MW、2.111 MW和0.093MW。在4种算法同时处于最优的MAPE和RMSE时,PSO-KELM的拟合度(最好)为0.890,RBFNN、LSSVM(较低)分别为0.782和0.801,GA-KELM拟合度略低于PSO-KELM。同时PSO-KELM最优的MAPE 较LSSVM、RBFNN 和GA-KELM的误差有所降低。可以说明PSO-KELM预测误差最小,且在仿真过程中具有良好的稳定性。

表3 3种模型误差对比

风电功率预测模型结果对比如图6所示。

图6 风电功率预测模型结果对比

在4种预测模型中,PSO-KELM更接近于真实曲线。

RPE误差点数统计如表4所示。

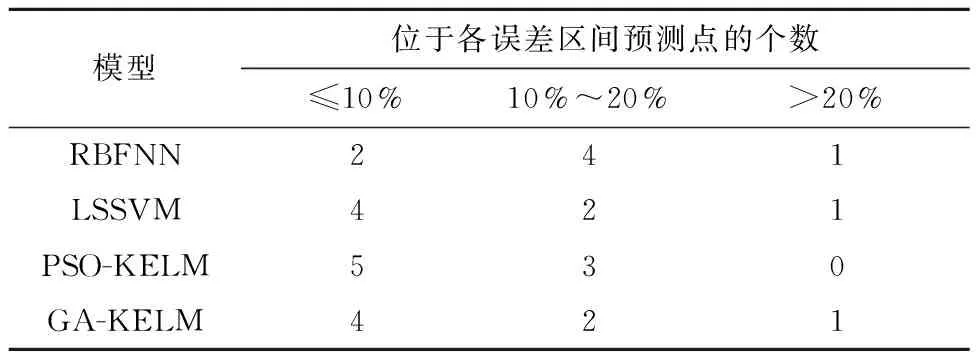
表4 RPE误差点数统计

由表4可以看出,在这4种模型前7个点中,PSO-KELM和GA-KELM算法在误差量小于10%范围内分布数目最多,分布较集中,波动性平稳。且PSO-KELM预测误差精度略优于GA-KELM。RBFNN和LSSVM预测算法误差分布较分散,波动剧烈,预测效果存在较大误差。

5 结 语

本文建立了KELM风电功率短期预测模型,适应度函数采用KELM 预测结果的MSE误差与粒子群算法优化KELM模型中惩罚因子和核参数,优化后的PSO-KELM模型预测效果更加精准稳定。实验证明,PSO-KELM算法较RBFNN、LSSVM和GA-KELM算法能够更准确地建立起风电功率短期预测模型,风力发电功率的预测精度更高。