基于改进传输线法的电器温度场并行有限元计算

邱子澜, 杨文英, 彭 飞, 翟国富

(哈尔滨工业大学 电器与电子可靠性研究所, 黑龙江 哈尔滨 150001)

0 引 言

电器产品的优化设计过程中,温度场的分析至关重要。高温会影响电器产品性能和质量,导致其机械强度、绝缘强度降低,金属元件氧化[1-2]。随着新能源的投入使用,大功率继电器、接触器等开关电器开始广泛应用于电动汽车、充电桩等用于接通大电流的场合中。此类电器功率大,温升问题明显,对其优化设计过程中的耐环境温度仿真提出了更高的要求[3-5]。此外,温度会影响电器的电、磁、机械等材料属性,在计算电器产品中其他场域,如电磁场分布时,为了实现更加精确的仿真,往往需要将温度耦合到求解过程中[6-7]。因此,精确而快速地求解电器产品的温度场分布具有重要意义。

电器中的热传递方式主要是热传导,传统的电器热传导计算通常采用热路法对模型进行简化[8],但是电器的三维几何结构复杂,使用热路模型计算电器温度场存在较大的误差。随着计算机性能的提升,有限元法成为电器热传导计算领域的主流方法[9-11]。为了更加精确地计算温度场的分布,需要考虑材料的非线性,对热传导而言主要体现在材料的热导率随温度变化[12--13],而非线性问题求解过程中所必需的迭代过程将进一步降低有限元方法的求解效率,因此如何提高迭代效率成为许多学者研究的问题。传统的迭代方法,如 Newton-Raphson(NR)法,依然是如今应用最广泛的迭代方法,实际应用过程中许多改良版的NR法被提出,如拟牛顿法或者引入松弛项,这些方法提高了NR法的收敛性以及求解效率[14],但是NR法每一次的迭代都需要重新装配Jacobi矩阵,因此改进传统NR法带来的效率提升有限。

相比于NR法,传输线法(Transmission Line Method,TLM)是一种更加适用于大规模非线性问题的迭代方法。TLM最早用于非线性电路的求解[15],后被逐步推广到有限元领域。文献[16]提出将TLM用于有限元非线性静磁学求解,在此基础上,文献[17-18]使用TLM,结合区域分解技术对三相感应电机的涡流进行了求解。已有学者研究TLM及其改进方法在电器产品电磁场求解领域中的应用,并取得较好加速效果。文献[19-20]将TLM应用于电器产品二维轴对称电磁场有限元的求解当中,并进一步将其推广到了含永磁的接触器的电磁场有限元求解。文献[21-22]提出了一种全新的黑盒传输线模型,该模型降低了有限元等效电路的复杂性,并且能够较好地处理有限元中非线性单元。文献[23]使用FPGA加速传输线迭代的计算,用于求解二维平面变压器模型的动态特性。文献[24]将TLM的入射过程改为节点区域分解,以较小的代价实现了传输线导纳的自适应更新,并且使得TLM适用于GPU异构计算。

尽管TLM在电器电磁场的求解中取得了很好的加速效果,但是鲜有学者将该方法用于电器温度场有限元的加速求解,并且该方法的求解效率有待进一步优化。因此本文提出使用TLM加速继电器三维热传导有限元的计算,在此基础上通过提出合理的传输线导纳确定原则、松弛迭代和并行计算进一步提高计算效率。本文首先介绍了TLM的原理,分析TLM的优点;之后,给出热传导有限元离散格式,并构建其等效电路;然后,针对具体的大功率直动式继电器模型,分别使用商用软件COMSOL,NR方法和TLM求解其温度场的分布,比较三者之间的求解精度差异,并比较不同分网条件下NR法和TLM间的求解效率差异;最后,对TLM在电器热传导求解中的应用前景以及存在的问题进行讨论和分析。

1 热传导有限元传输线模型的建立

1.1 TLM原理

TLM的基本原理是,在线性电路网络和非线性元件之间添加一段无损传输线,通过传输线两端电压的传递来实现迭代,从而实现非线性电路的求解[25]。TLM基本原理如图 1所示。

图1 TLM基本原理

电路中,电阻R为非线性元件,在线性电路网络和非线性电阻R之间插入传输线,原有的电路被分解成入射过程和反射过程。其中,入射过程等效为一个大型的线性电路网络,反射过程被分解成多个简单的非线性等效电路。入射与反射两部分交替求解,最终结果将收敛于真实值。

在非线性电路中,传输线迭代法的优势体现在:①传输线的添加并没有使电路的本质发生改变,如果所求解电路系统存在稳定状态,那么传输线迭代也会存在一个稳定状态,即TLM是无条件收敛的;②对于入射过程待求的YU=I这一线性方程组,每一步迭代过程的导纳矩阵始终不变,这意味着如果采用LU分解来计算迭代过程中的线性方程组,传输线只需要在第一步迭代时执行LU分解,而LU分解是求解过程中耗时最长的部分,因此TLM的单步计算时间可显著缩短;③非线性迭代过程被放在多个分立的简单电路中完成,实现了各个非线性元件的分立,有利于非线性迭代过程的并行化计算。在有限元分析中,将有限元模型等效成电路,应用传输线迭代法进行计算,其优点则体现为无条件收敛、单步迭代时间显著缩短以及非线性单元的细粒度并行化计算。

1.2 非线性热传导有限元分析

为了将TLM应用到非线性热传导有限元分析当中,首先需要得到热传导有限元的离散格式,进而推导出有限元等效电路。根据傅里叶定律,热传导问题的算子方程及其边界条件[26-27]为

(1)

式中:λ(T)——热导率,随温度变化;

T——求解域内的温度;

Tg——边界温度;

G——内热源强度;

n——边界平面的法向向量;

q——热流密度;

h——对流换热系数;

Ω——求解域;

Γ1——第一类边界条件;

Γ2——第二类边界条件;

Γ3——第三类边界条件;

T0——周围介质温度。

可见在求解域中,温度场满足Poisson方程。接下来讨论温度场中的三类边界条件。

第一类边界条件:强迫边界条件,边界上的温度或温度分布函数已知。

第二类边界条件:热传导边界条件,边界上的热流密度(热通量)q已知。

第三类边界条件:对流边界条件,边界与周围环境介质的对流传热系数h和介质温度T0已知。

通过伽辽金法,上述控制方程和边界条件可离散为一组积分方程[28]

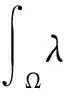
(2)

式中:Tj——空间内各个离散点的待求温度;

Ni、Nj——形函数。

采用四面体单元对模型进行离散,将每个单元整理成形如[Se][Ae]=[Fe]的代数方程组,可得矩阵中的每一项为

(3)

其中,

式中: [ST]、[FT]——四面体单元分析产生的项;

[Se]、[Fe]——等效为节点、矩阵、电流源;

[SB]、[FB]——边界条件产生的项;

(xk,yk,zk)、(xlk,ylk)——四面体单元和三角形单元的节点坐标。

计算所有的四面体单元及其边界并进行总体合成,可以得到全局的代数方程组:

[S][T]=[F]

(4)

1.3 有限元等效电路构建

将TLM应用于有限元分析,其理论依据为有限元分析中,单元系数矩阵[Se]是对称正定矩阵,因此对于有限元法中每个单元方程组[Se][Te]=[Fe],可以将其等效为电路的形式。其中,[Te]等效为节点电压,而有限元中的装配过程,可以理解为将多个电路并联在一起。因此,可以构建有限元等效电路,从而将TLM应用于有限元的求解过程中。四面体单元等效电路模型如图2所示。

图2 四面体单元等效电路模型

分析单元入射过程等效电路,可以得到单元的导纳矩阵[Ye],单元的激励向量[Fe]和单元的电流向量[Ie]。将所有子电路并联,TLM有限元等对应有限元分析中的总体合成,得到一个线性方程组:

[Y][U(k)]=[F]+[I(k)]

(5)

式中: [Y]——全局导纳矩阵;

[U(k)]——等效节点电压;

[F]——原始激励向量;

[I(k)]——传输线等效电流源。

图3 TLM有限元等效电路模型

直到全局误差ε小于最大误差εmax时达到收敛。ε的计算方法为

(6)

式中:n——节点数目;

U——全局节点电压。

2 TLM求解效率提升

尽管相比于传统的NR法,TLM的单步迭代时间可以显著减少,但是NR法可以达到n2的收敛阶,而TLM的收敛阶为logn,针对相同的非线性问题,传输线迭代法的迭代次数要大于传统的NR法。因此,本文提出合理的传输线导纳确定原则、松弛迭代以及并行计算方案,以进一步提高TLM效率。

2.1 传输线导纳确定原则

选择合适的传输线导纳可以显著减少迭代次数,传输线导纳越接近于所连接的导纳真实值,TLM收敛速度越快。针对这一特性,本文提出基于外部环境温度的传输线导纳确定原则。

对于传输线两侧连接的非线性元件,根据有限元TLM原理,可知其导纳的真实值Yt为单元系数矩阵非对角元素的值的相反数,即

(7)

其中,单元热导率λe是受温度影响的变量,其余参数仅仅和单元的几何形状相关,是已知量。为了使得传输线导纳Y0尽量接近于Yt,本文将每根传输线的导纳设置成不同的值,确保传输线导纳Y0和单元的几何参数构成线性关系,即

(8)

式中:λg——热导率的初始猜测,求解前需要配置该参数。

对于热传导有限元而言,该方案容易进行,这是因为热传导模型中,热导率随温度变化并不显著,因此可以在传输线迭代前,将外部环境温度代入模型,得到当前温度下非线性单元的热导率,进而通过式(8)计算得到传输线导纳的值。

经测试,设置λg与非线性材料的真实值在同一数量级,即可保证较少的迭代次数。

2.2 松弛迭代

反射过程中,需要求解nTL个如图3(b)的非线性电路,直接使用NR法求解该电路存在一定的困难。一方面,该电路中非线性导纳是所在单元热导率的函数,和当前电路的参数并无直接关联,这使得NR法关系式难以构建;另一方面,频繁的分布式非线性迭代将进一步影响求解效率。

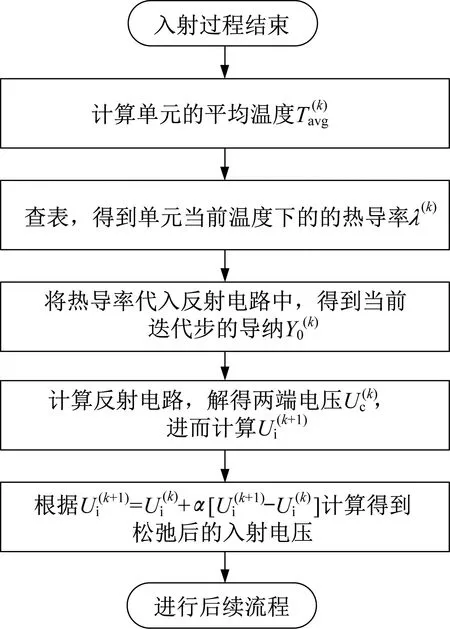
图4 反射过程中的松弛迭代流程

(9)

2.3 并行计算

为进一步提高求解效率,充分发挥多核处理器的性能,本文提出CPU并行计算方案来加速整个求解过程。TLM热传导有限元求解流程如图5所示。其中设置边界条件和负载、计算单元系数矩阵、装配有限元TLM等效电路、反射过程可实现单元级别并行,本文使用OpenMP实现上述流程的并行化。入射过程涉及到线性方程组计算,需要进行LU分解以及矩阵-向量乘法,本文使用SuperLU_MT[29]这一并行矩阵求解器实现入射过程的并行化。

图5 TLM热传导有限元求解流程

3 算法验证

3.1 研究对象

为了验证TLM在电器温度场计算中的求解精度和求解效率,本文选用模型进行求解。直动式继电器结构示意图如图6所示。该模型为一个典型的大功率直动式继电器,额定负载为270 V/200 A,模型已处在吸合状态。组件材料及热导率如表1所示。

图6 直动式继电器结构示意图

表1 组件材料及热导率

继电器工作过程中,有线圈通电发热与触点接触电阻两部分发热。设置线圈电压U=28 V,线圈电阻R=170 Ω,线圈体积V=2.2×10-5m3,由计算可知线圈内热源强度G1=2×105W/m3。假设接触等效部分为静触头和动触头之间的一个等效圆环体,根据继电器额定负载接触电阻计算公式[27],得到接触部分内热源强度约为G2=105W/m3。此外,继电器通过空气自然对流散热,该模型所有的边界均定义为热对流边界条件,设置传热系数h=25 W/(m2·K),外部温度T0=293.15 K。

3.2 结果对比

首先对比商用软件COMSOL、NR法以及TLM三者的求解精度。设置最大收敛误差为10-9,四面体分网单元数目为174 825,通过3种方法分别对模型进行求解,得到温度场分布散点图。COMSOL、NR、TLM温度场散点图对比如图7所示。由图 7可知,在相同的参数设置下,3种求解方法得到的温度场分布趋势和温度范围基本一致。

图7 COMSOL、NR、TLM温度场散点图对比

随机选取10个分网节点,得到COMSOL、NR和TLM 3者的求解结果,节点坐标及计算结果如表 2所示。

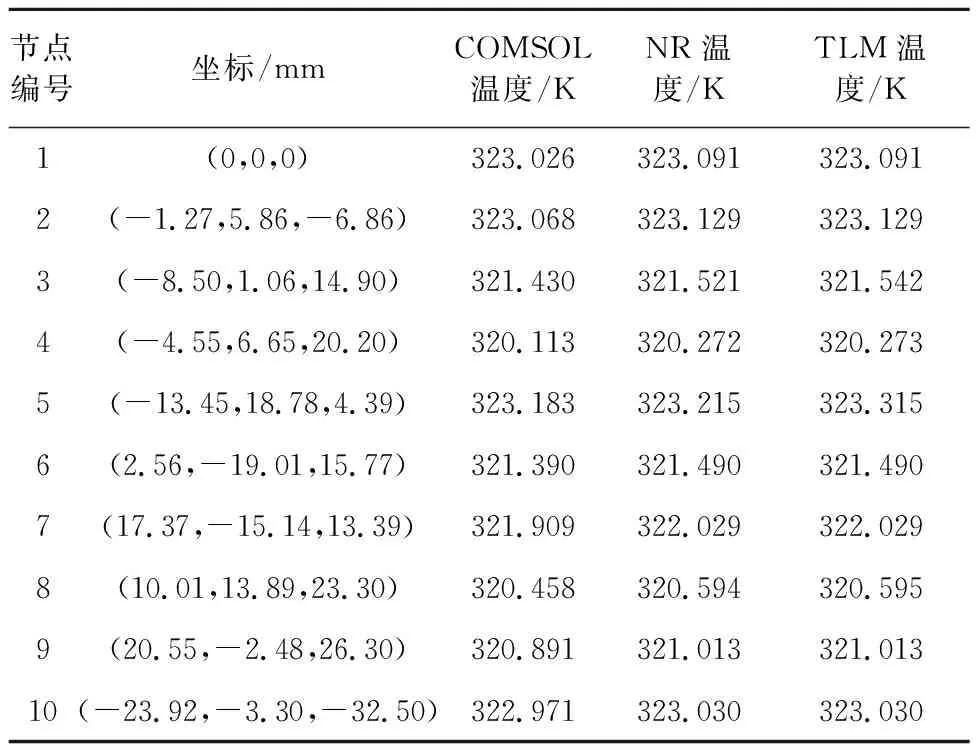
表2 节点坐标及计算结果

以COMSOL的求解结果为参照,定量分析NR方法和TLM之间相对误差。NR和TLM相对误差分析如表3所示。其相对误差的计算方法为

表3 NR和TLM相对误差分析

(10)

其中,T取TNR或TTLM。

分析表 3的数据,可见在计算条件一致的情况下,NR和TLM相对COMSOL的计算误差能够保持在0.1%之内,本文采用的算法能够满足精度要求。

对比不同单元数目下NR和TLM间的求解效率。求解所用计算机的CPU为Intel Core i7-9700,8核8线程,内存大小为32 GB DDR4。两种方法均使用并行的线性矩阵求解器SuperLU_MT进行方程组计算,并创建8个并行线程,以充分释放CPU的性能。本文选择了4组分网模型对TLM进行测试。不同分网条件下NR和TLM的迭代次数和单步迭代时间分别如表4所示。可见,NR的迭代次数要少于TLM的迭代次数,但是TLM单步迭代时间相比于NR迭代时间显著缩短,并且随着分网单元数目的增加,TLM单步迭代时间优势更显著。这是因为TLM每一次迭代的左侧系数矩阵不变,只需要在第一次迭代进行LU分解,而后续迭代过程不需进行额外的LU分解。因此TLM能获得单步求解效率的显著提升。

表4 NR和TLM迭代次数和单步迭代时间对比

NR与TLM全局求解时间对比如图8所示。相比于NR法,TLM方法求解效率更高。TLM的第一次迭代需要进行LU分解,占据大量时间,这一迭代过程和NR单次迭代所消耗的时间基本一致。TLM后续迭代过程中,尽管单步迭代时间极小,但是过多的迭代次数也将产生一定求解耗时。随着求解规模的增大,TLM后续迭代过程所占用的全局求解时间比例随之减小,这也使得TLM的求解加速效果更加显著。针对本模型,在单元数目较多时TLM可以取得相对于NR法2倍以上的加速比。

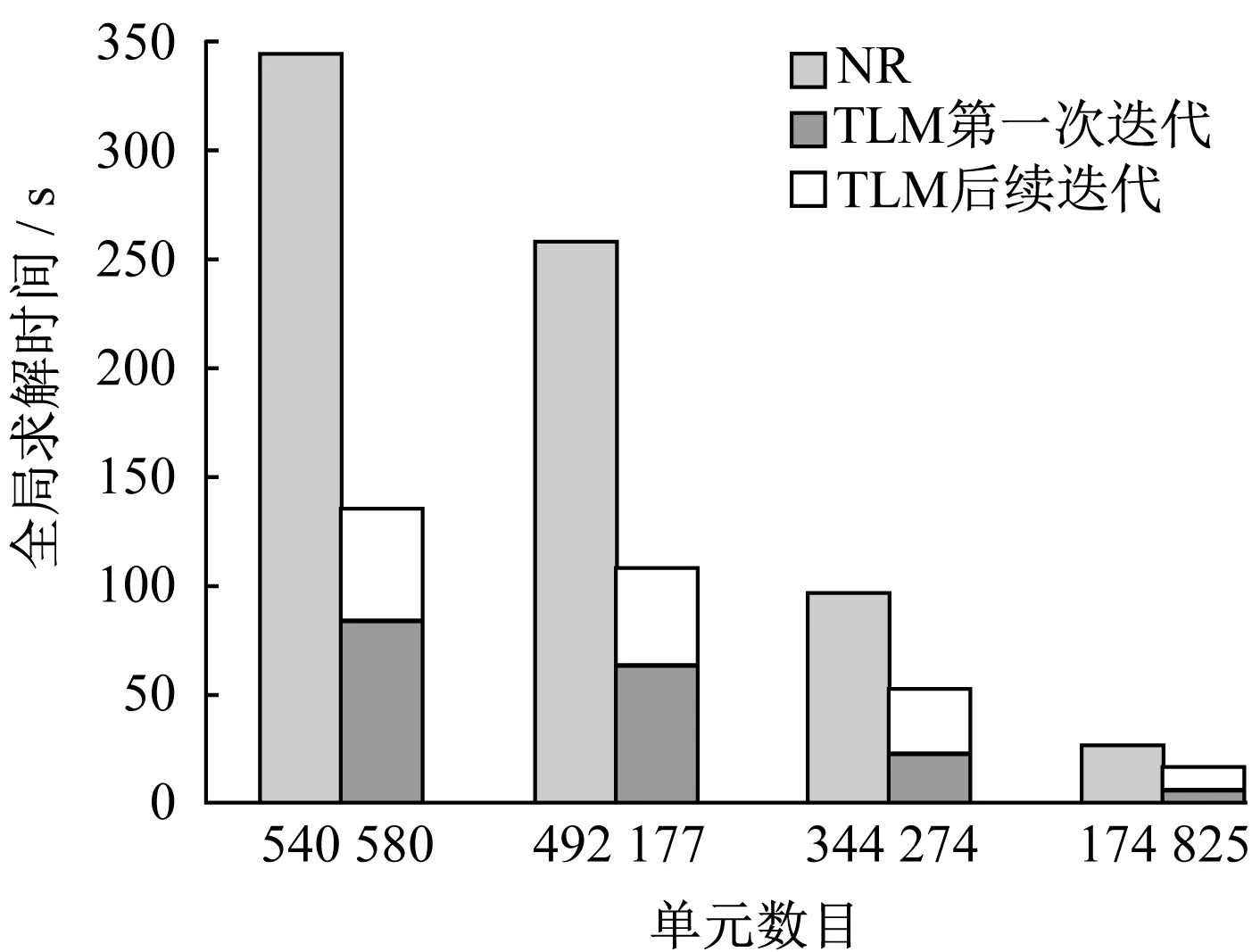
图8 NR与TLM全局求解时间对比

4 结 语

本文提出使用改进的传输线迭代法加速三维热传导有限元问题的求解,并将其应用于继电器温度场的求解中。针对热传导有限元问题的计算,该方法可以获得和商用软件一致的求解精度。相比于NR法,TLM可以通过缩短单步迭代时间的方式取得较高的求解效率,然而TLM的迭代步数较多,制约了迭代效率,因此依赖预处理过程来减多迭代步数,即选择合适的传输线导纳。在选择合适的预处理方案的前提下,模型规模越大,TLM的加速效果越明显。可见TLM适用于大规模非线性温度场有限元的计算,在电器热仿真和多物理场耦合中具有广阔的应用前景。

为进一步提高TLM的求解效率,后续研究可围绕以下3个方面展开:提高LU分解的效率,以解决第一步迭代时间过长的问题;选取更加合适的传输线导纳初始猜测,进一步减少迭代次数;在保留TLM只进行一次LU分解这一显著优势的条件下,研究通过自适应方式更新传输线导纳的方案,从而提高TLM的收敛阶。