基于ADMM的光储电动公交充电站分布式优化策略*

何 鑫, 李 征, 孙国歧, 魏晓宾, 蔡 旭, 曹云峰

(1.东华大学 信息科学与技术学院, 上海 201620;2.山东德佑电气股份有限公司, 山东 淄博 255088;3.上海交通大学 电子信息与电气工程学院, 上海 200240)

0 引 言

随着环境和能源问题的日渐凸显,光伏这一清洁能源更加得到重视。光伏发电作为分布式发电的一员,其运行非常灵活。配合储能系统既可以孤岛运行又可以并网运行[1-3]。电动公交作为公共交通中的一员,其配套的光储充电站可以作为光伏系统的有效消纳,但是公交汽车充电功率较高,同时充电会产生负荷高峰,因此对于光储公交充电站的经济优化问题成为关注的焦点。

目前,针对充电站的有序充电及其与光伏储能配合的联合优化开展了许多研究。文献[4]研究了分时电价收费机制下的电动汽车有序充电策略,通过电价以及储能系统对电动汽车充电进行引导,达到了减小购电成本和缩减负荷方差的作用。文献[5]在光伏充电站引入储能设备,建立光储容量配置的模型,运用遗传算法求解得出最佳储能容量以实现光伏的最大利用。文献[6]建立电动汽车充电站的双层优化模型,上层以配电网负荷波动最小为目标,下层以充电站实际充电方差为目标,仿真结果表明峰谷差有明显减少。文献[7]为了减少配电网扩容压力,对电动汽车充电站引入储能系统提高设备利用率,达到减低电池损耗的作用。文献[8]分析了光伏充电站运行中的优化调度问题,提出了购电费用最低和储能循环电量最小值的多目标优化调度模型,使用非支配排序遗传算法进行求解。文献[9]提出多条公交线路的光储公交充电站优化策略,以最小化充电站运行成本为目标,考虑了多场景下光伏出力,通过排队理论进行改进,可以有效地降低充电站光储设备投入成本。

充电站的经济优化多使用集中式控制策略[10-11],通过调度中心采集所有信息并进行调度,而分布式控制能够达到更好地匹配不同主体的目标[12-13]。文献[14]提出一种分布式有序充电控制策略,以最小配电网负荷方差为目标优化电动汽车充电。文献[15]采用分布式电动汽车充放电分层管理框架,建立了电动汽车智能体最大化自身利益优化模型和运营商峰谷差的优化调度模型,并兼顾了各层次的效益。文献[16]提出兼顾电网、电动汽车和车主三方利益的多目标分布式优化模式,将全目标拆解为各设备独立的子问题,通过分布式算法进行求解,验证了分布式算法在计算时间和各目标优化结果上比集中式优化具有优势。

上述研究针对光储电动公交充电站这一特殊主体的还较少,且均采取集中式优化。这造成大量数据集中处理,增加了计算时间,存在规定迭代次数或者时间内寻不到最优解的情形。分布式优化则可以通过把全目标拆分成子目标求解,故而克服这个缺陷。另外,上述研究均未考虑在一定光伏渗透率下储能容量利用率的优化问题。本文将针对电动公交大规模接入光储充电站的情形,建立以公交车充电成本最低和光储联合收益最大为目标的光储电动公交充电站优化模型,并在各类光伏充电站工况下充分考虑储能剩余利用。引入交替方向乘子算法(Alternating Direction Multiplier Method,ADMM),将集中优化问题转换为以公交车和光储为主体的子优化问题求解,使用实际运行数据仿真验证其有效性和可行性。

1 光储公交充电站的系统结构及运行策略

1.1 系统结构

电动公交汽车需要能进行较快的充电以尽可能减少车辆数量的投入,因此广泛采用高压直流充电方式。光储公交汽车充电站主体主要包括配电变压器、光伏阵列、储能系统、直流充电桩和电动公交车。光储公交充电站结构如图1所示。

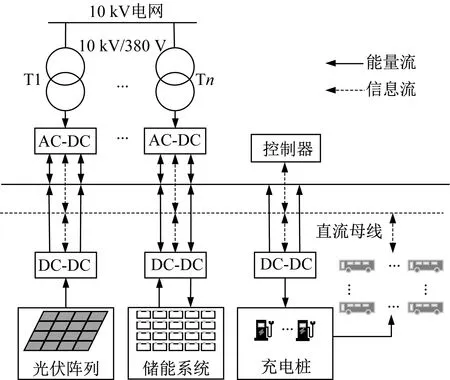
图1 光储公交充电站结构

1.2 光储公交充电站的运行策略

在光储充电站中,往往以光伏优先使用为准则,储能能量的来源为光伏和低售价时的电网,系统的运行有如下几种工况:

(1)光伏(工况1):该工况下直流母线的能量都由光伏供应,并且时间段处于电网低价售电时,在保证充电负荷前提下,多余的电能存入储能系统,若电池容量已满,则向电网售电。

(2)光伏和储能(工况2):该工况下直流母线的能量由光伏和储能电池一起提供,应用于光伏发电功率不足以满足充电负荷要求情形。

(3)储能(工况3):该工况下直流母线的能量由储能电池提供,应用于储能容量能够满足充电要求情形。

(4)光伏、储能和电网供电(工况4):该工况下直流母线能量由电网、储能和光伏同时供应,应用于光伏系统少出力并且储能系统容量不足以提供足够能量或剩余需求超过储能的最大输出功率的情形。

(5)光伏和电网供电(工况5):该工况下直流母线的能量由电网和光伏一起供应,应用于光伏系统少出力不足以满足充电负荷情形。

(6)储能和电网供电(工况6):该工况下直流母线的能量由电网与储能系统供应,应用于光伏系统在无出力且储能系统处于容量充足情况下。

(7)电网供电(工况7):该工况下直流母线的能量由电网单独提供,光伏系统处于弱光照或无光照的出力状态。

(8)光伏(工况8):该工况下直流母线能量由光伏提供,并且时间段处于电网高售电时间段,在保证充电负荷前提下,多余的电能流向电网,向电网售电。

分析8种光储公交充电站运行工况的输入能量来源、输出对象和可否向电网售电情况。运行工况状态如表1所示。

表1 运行工况状态

各工况在高电价的峰时段以及中低电价的平谷时段的切换条件主要取决于光伏功率Ppv、负荷需求Pload和储能荷电最大SOCmax与最小SOCmin的阈值,峰电价时间段、平谷电价时间段工况切换条件分别如表2和表3所示。同一条件下不同工况选择主要取决于储能电能的来源以及储能输入/输出功率阈值。

表2 峰电价时间段工况切换条件

表3 平谷电价时间段工况切换条件

2 光储公交充电站分布式优化模型

2.1 目标函数

光储公交充电站的经济优化需要电动公交的调度和光伏储能系统的配合。本文把电动公交和光储系统作为优化的两个主体,充分考虑每个主体的目标。

2.1.1 电动公交汽车目标函数

电动公交车具有计划性,每日任务相对固定。电价计费标准为由电度电价和需(容)电价组成的两部制电价[17],并且电费按月收取,因此属于运营商的公交汽车首要目标为确保每月向电网购电费用f1最小。

minf1=C1+(1-λ)C2+λC3-C4

(1)

式中:C1——电度电价下收取的每月电费;

C2——按照负荷尖峰收取的每月需量电费;

C3——按照变压器额定容量收取的每月容量电费;

C4——每月向电网售电收入;

λ——收费机制标志位,“0”表示按照需量电费收费,“1”表示按照容量电费收费。

其中,

(2)

C2=d1·Pmax

(3)

C3=d2·SN

(4)

(5)

式中:Dd——每月第d天充电所产生的电度费用;

D——该月的天数;

d1——需量电费价格;

Pmax——每月15 min平均负荷的尖峰值;

d2——容量电费价格;

SN——变压器容量;

(6)

(7)

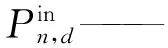
T——以Δt为间隔的时间段个数;

Sn——n时刻的电度电价;

Δt——时间间隔;

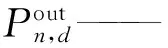
2.1.2 光储系统目标函数

光伏和储能合理配合可以较好地解决光伏消纳问题,装设光伏储能系统的充电站需要合理调度,确保光伏系统的发电量和储能系统容量达到最大的利用,即光储总发电量的效益f2最高。

(8)

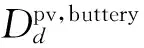
(9)

(10)

(11)

(12)

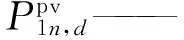
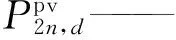
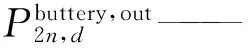
ΔS——峰时电费与谷时电费的差值;

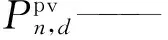
2.2 约束条件

2.2.1 光伏充电站工况约束

根据电网售电时刻,分为电网中高价售电时间和低价售电时间段。

当处于中高售电价格时,如表2中光伏充电站可以工作在工况2、工况3、工况5、工况7、工况8下,其各个工况下需要满足的功率平衡为

(13)

当处于中低售电价格时,如表3中光伏充电站可以工作在工况1、工况2、工况3、工况4、工况5、工况6、工况7下,其各个工况下需要满足的功率平衡,即

(14)

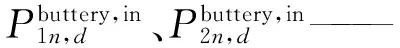
在任意时刻光储充电站都需要满足功率平衡约束为

(15)

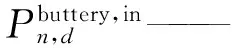
2.2.2 电池充放电电量约束

电池一天工作的充放电电量满足平衡,即充电电量与放电电量相等。

(16)

(17)

2.2.3 储能充放电功率约束

(18)

(19)

2.2.4 功率需求约束

根据每日的排班历史数据可得,公交车第m辆车的到站时刻矩阵Tbin,m、发车时刻矩阵Tbout,m和进站时车辆电池电量Ein,m:

Tbin,m=[tbin,m,1,tbin,m,2,…,tbin,m,j]

(20)

Tbout,m=[tbout,m,1,tbout,m,2,…,tbout,m,j]

(21)

Ein,m=[Ein,m,1,Ein,m,2,…,Ein,m,j]

(22)

式中:tbin,m,j——该日第m辆车第j次任务的进站时间;

tbout,m,j——该日第m辆车第j次任务的出站时间;

Ein,m,j——该日第m辆车第j次任务后的进站电量。

(23)

(24)

通过车辆参数和排班线路数据可以求得第m辆车在j任务的需求电量:

式中:Em,j——第m辆公交车的第j次任务的损耗电量;

m——公交车总重;

g——重力加速度;

f——摩擦系数;

Cd——风阻系数;

A——迎风面积;

μ——车辆传动效率;

L——线路长度。

车辆在站的最低需求充电功率Pneed:

式中:αm,j——标志位,表示第m辆车第j次进站是否有充电需求,有则为“1”,没有则为“0”;

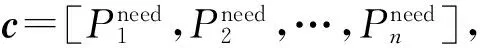
(30)

式中:βm,n——标志位,表示第m辆车第n个时间段内是否在站,在站则为“1”,不在站则为“0”;

Mn,need——第n个时段上电池电量不满的车辆个数;

3 优化算法

ADMM是求解分布式算法的方法之一,其为对偶上升法和乘子法的演变,吸取了这两种方法可分解以及收敛好的特点。其解决问题的核心思想就是对于问题的拆分,即将大问题拆分为若干个小问题,进行变量的交替求解,并更新求解后的对偶变量,得到最终的共同收敛。所以称之为“交替方向乘子法”[18],并且适用于统计学、机器学习等大规模分布式凸优化问题,其标准形式如下。

(31)

式中:f()、g()——2个凸函数;

x、z——2组变量；

A、B、C——常量参数。

其中,x∈Rn,z∈Rm,A∈Rp×n,B∈Rp×m,c∈Rp。

构造增广拉格朗日函数:

Lp(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-c)+

(32)

式中:λ——拉格朗日乘子;

ρ——惩罚项的惩罚因子。

其中,λ∈Rp,ρ>0。

ADMM能够在循环内解决目标函数,在k+1次循环的计算更新操作:

(33)

由式(33)可知,x的第k+1次迭代采用第k次z和λ的迭代结果,z的第k+1次迭代采用第k+1次x和第k次λ的迭代结果,λ的第k+1次迭代则采用了第k+1次z和x的迭代结果。因此本方法的迭代是一种交替上升的思想。

通过ADMM算法将用电成本和光伏收益两个目标函数的变量之间进行相互迭代求解。为了使各变量可以同步迭代,并且能够在本地进行独立求解,可选取所有变量上一次迭代计算结果的平均值作为相邻变量的更新值。

(34)

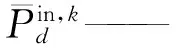
另外将不平衡功率ek进行以下表示:

(35)

(36)

根据ADMM原理,上述迭代过程的终止条件为原始残差和对偶残差需要同时满足收敛精度。

(37)

式中:εprimal、εdual——原始残差收敛精度和对偶残差收敛精度,均取为1×10-3。

图2 算法求解流程

4 算例分析

为了验证ADMM算法在光储公交充电站经济优化的有效性,以某市公交枢纽为数据来源进行仿真,选取典型日负荷数据和光伏典型出力曲线。

充电站配电网选用4个SCB-10干式变压器,额定容量为1 250 kVA。通过聚类分析,典型工作日和周末负荷曲线如图3所示。为了实现2060年的碳中和,渗透率需要达到一定要求,本文渗透率为30%,光伏取充电站容量的30%,光伏典型出力曲线如图4所示。两部制电价收费如表4所示;储能和光伏系统参数如表5所示。

表4 两部制电价收费

表5 储能和光伏系统参数

图3 典型工作日和周末负荷曲线

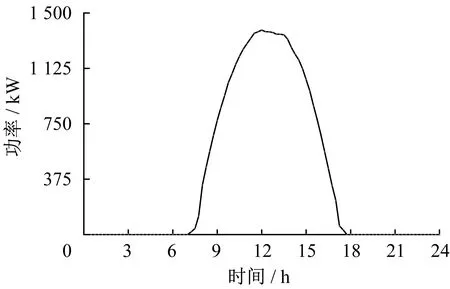
图4 光伏典型出力曲线

本策略储能可以从电网获取能量,假定初始时刻储能容量在50%,并且其能量来源于谷时电网与光伏。光储公交充电站典型工作日和周末优化后的工况状态分别如图5、图6所示。

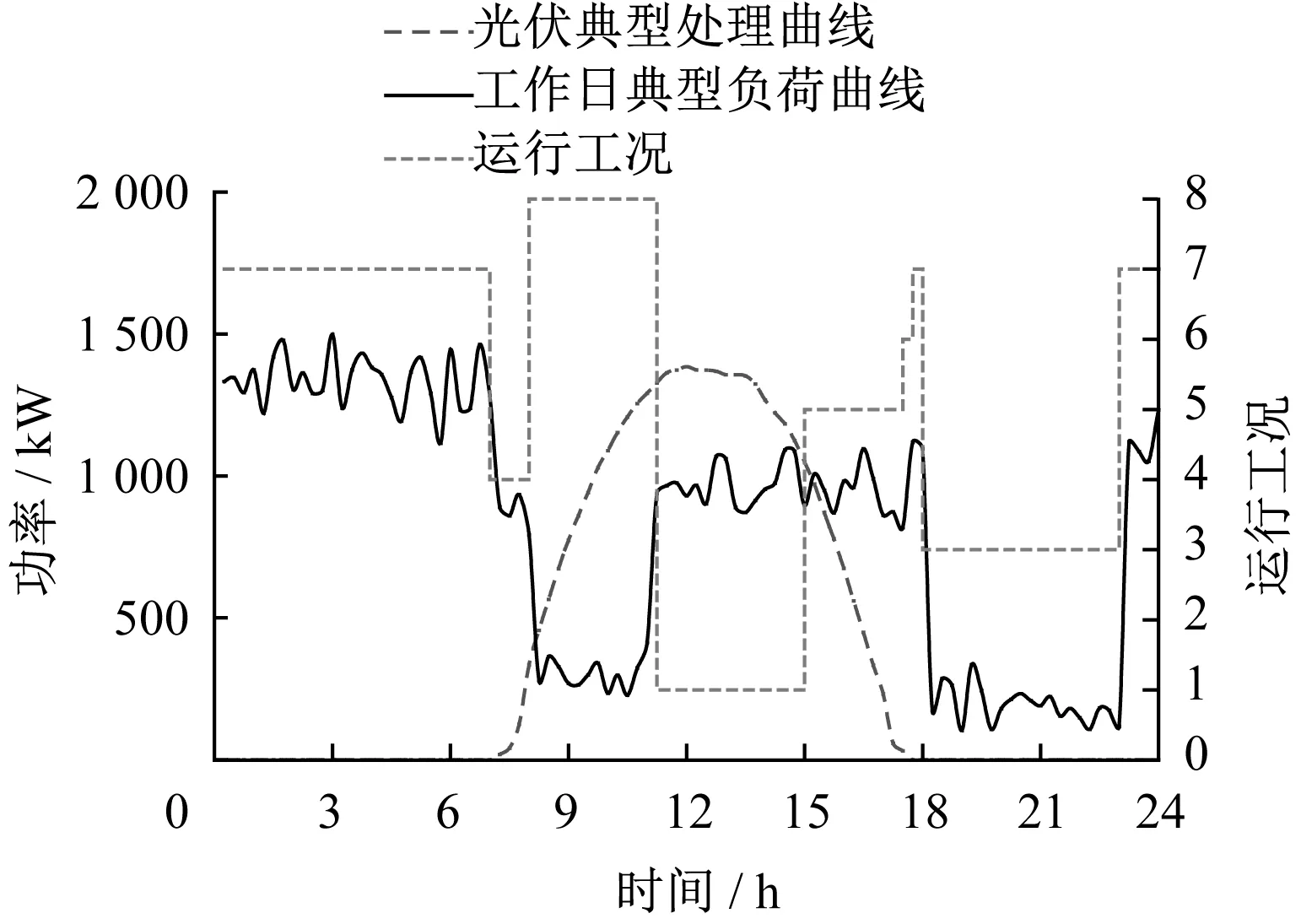
图5 光储公交充电站典型工作日优化后的工况状态

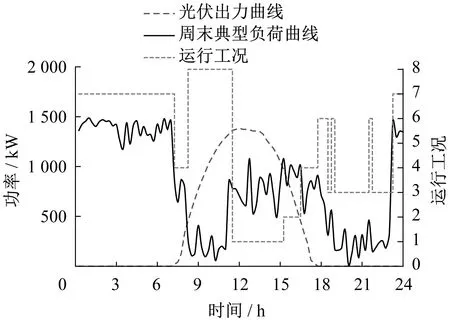
图6 光储公交充电站周末优化后的工况状态

常规光储充电站在光伏发电时使用光伏发电,若光伏发电超过负荷需求,则使用储能进行存储,等到光伏出力不足时刻进行释放。在储能满容量且光伏出力较高时存在弃光现象,并且对于日常充电负荷没有进行调度。常规光伏调度策略后典型工作日和周末光伏出力、电网输入功率、储能充电和放电功率曲线分别如图7、图8所示。

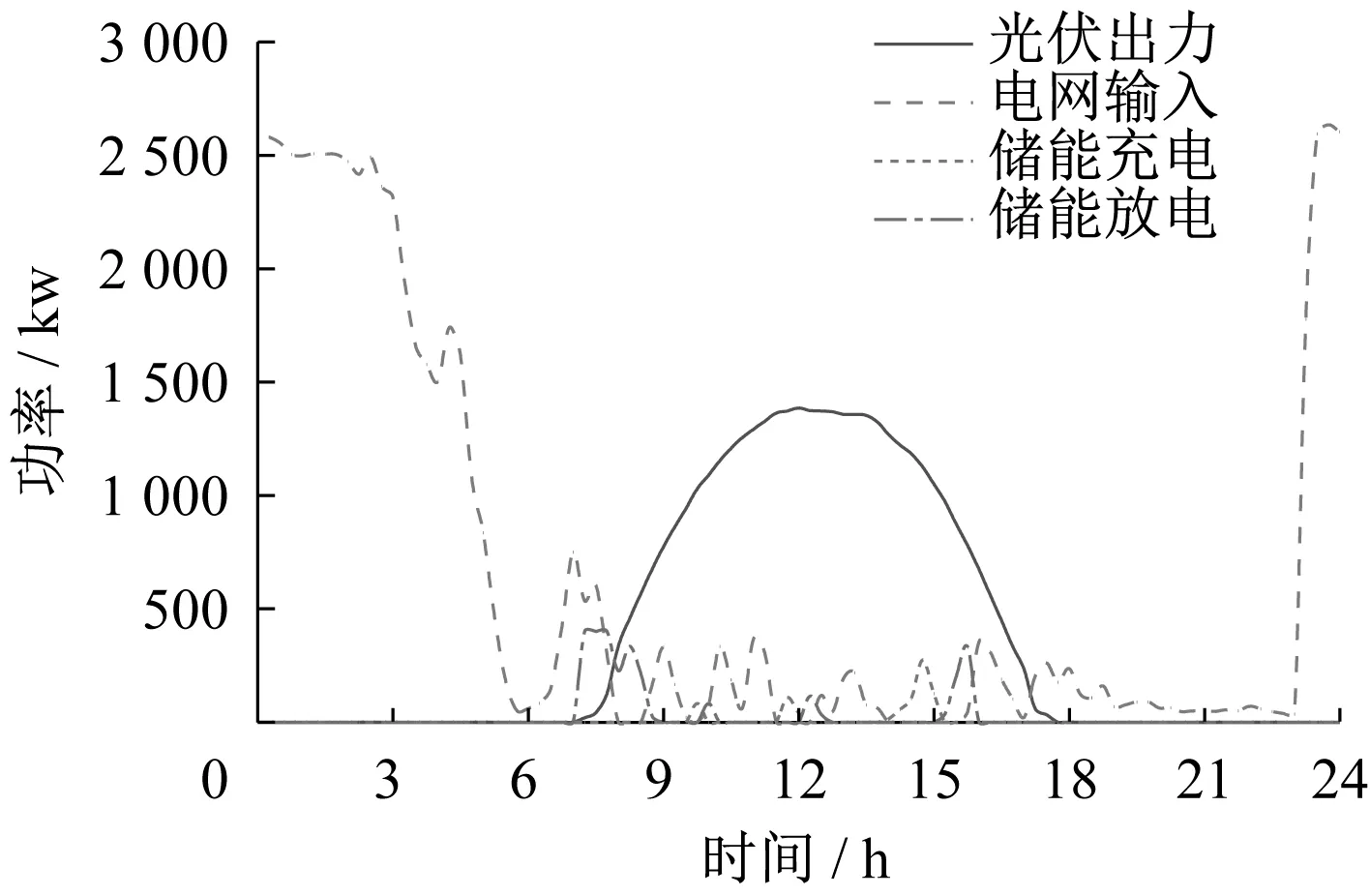
图7 常规光伏调度策略后典型工作日光伏出力、电网输入功率、储能充电和放电功率曲线

图8 常规光伏调度策略后周末光伏出力、电网输入功率、储能充电和放电功率曲线

在图7、图8中,可以消纳光伏的输出,但是对于储能的来源只是光伏,调度不灵活。在周末会出现光伏弃光现象,且并未优化其充电负荷。本文策略增加向电网售电情形以及储能从电网充电状况,并且通过调度车辆改变其原有的充电负荷在时序上的分布。通过ADMM算法进行优化,分布式调度优化策略后典型工作日和周末电网输入、充电站售电、储能充电和储能放电功率曲线分别如图9、图10所示。

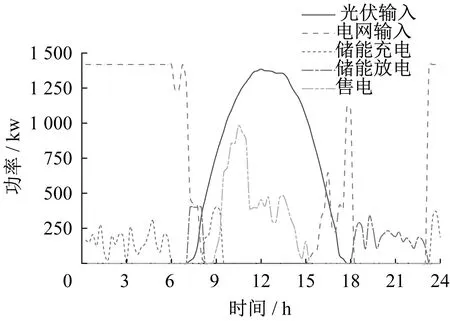
图9 分布式调度优化策略后典型工作日电网输入、充电站售电、储能充电和储能放电功率曲线

图9与图7相比较,在夜晚谷时电价较低时,储能系统可以补充电量在峰平时刻输出,表现为在8∶00～11∶00的峰时刻有效减少了电网输入,并且通过负荷调度使得夜晚的负荷峰值明显地下降。在白天的高出力区间9∶00～15∶00,光伏可以通过售电解决光伏出力过高和储能容量限制的问题。图10与图8相比较,在夜晚时刻储能系统可以从电网进行充电,其电能主要集中在光伏无出力的18∶00～23∶00的峰时刻提供电能,同时周末负荷在9点～17点需求小于光伏出力,并且储能容量不足以存储所有电能,产生了向电网售电的情形,相比于常规调度的弃光更加经济。通过负荷调度,使得夜晚的负荷峰值明显地下降。常规调度策略与分布式调度优化策略后主要参数对比如表6所示。

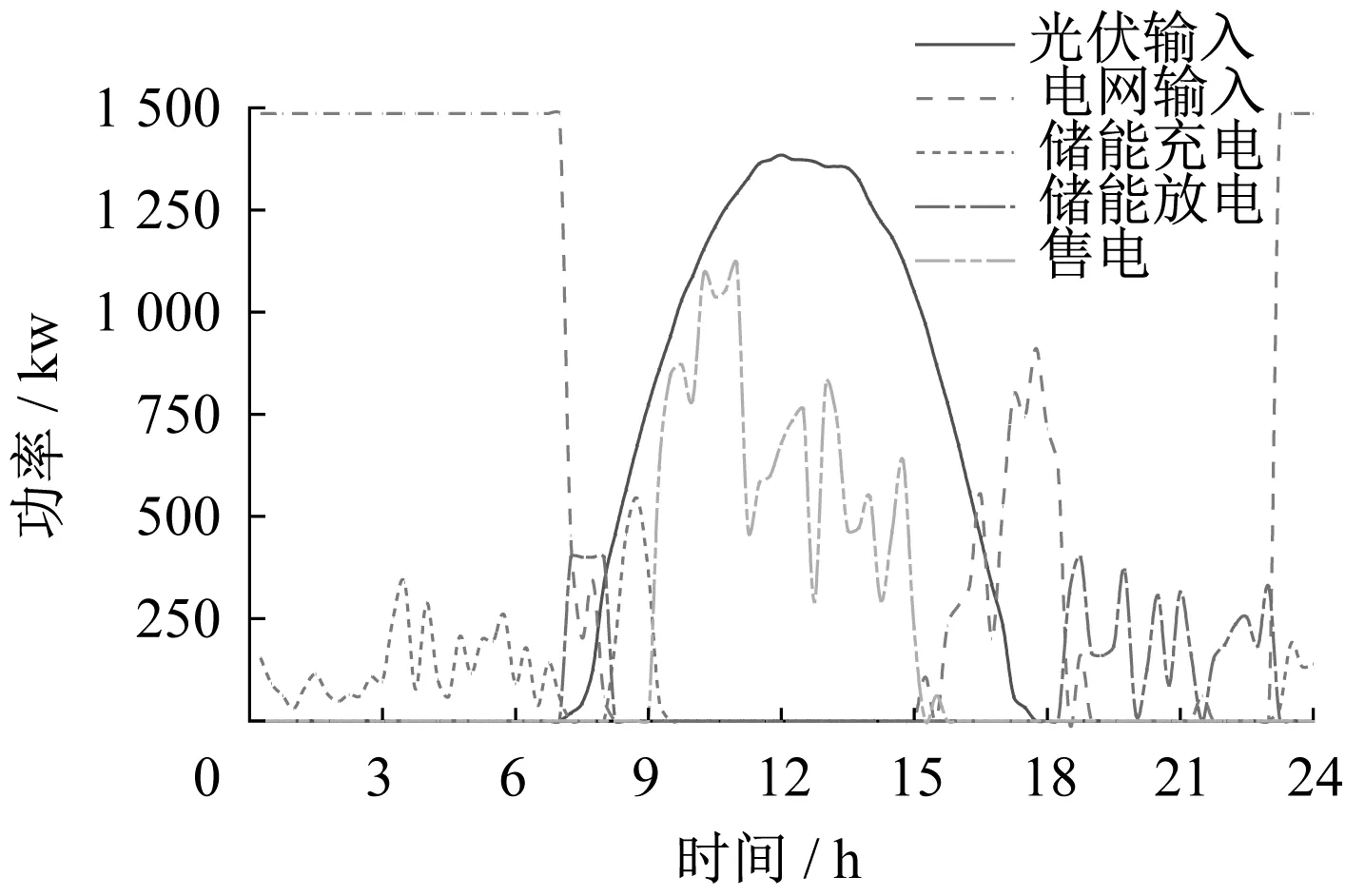
图10 分布式调度优化策略后周末电网输入、充电站售电、储能充电和储能放电功率曲线

表6 常规调度策略与分布式调度优化策略后主要参数对比

标准月取22个工作日与8个周末,月主要参数对比如表7所示。

表7 月主要参数对比

为了验证分布式算法在收敛和寻优解上具有优势,以典型工作日负荷为例,分别使用ADMM算法与集中式粒子群算法(MPSO)求解,将充电费用目标函数的解迭代曲线进行比较。分布式算法与集中式算法迭代曲线如图11所示;两种优化算法用电费用对比如表8所示。由图11和表8可见,在相同迭代次数下分布式优化算法能够找到更优解,并且在同一充电费用下其迭代速度更快。

图11 分布式算法与集中式算法迭代曲线

表8 两种优化算法用电费用对比

5 结 语

本文以光储充电站为研究对象,建立了公交充电成本最低和光储联合收益最高为目标的光储电动公交充电站优化模型,并针对该优化模型使用 ADMM 算法求解,与传统集中算法相比,ADMM 算法具有更快的收敛速度,且能找到质量更高的解。仿真结果表明,本文所建模型与所用算法对光储充电站的优化调度具有很好的效果,比常规调度策略降低了56%充电费用,同时提高21%的光储联合收益,其中80%的充电节省费用来自于售电节省,剩余20%为通过充电负荷的调度与光储运行工况的配合所节省。本文的光储充电站优化策略可为光储充电站的经济调度问题提供参考。