隔离半桥电路建模及补偿参数设计*

金宁德, 王海欣, 黄海宏

(合肥工业大学 电气与自动化工程学院, 安徽 合肥 230009)

0 引 言

隔离半桥电路由两个功率开关组成,相比于全桥电路,结构较为简单,对于非隔离DC/DC变换器,隔离半桥电路中的变压器可以避免输入端的干扰影响输出电压的稳定性,并且其功率范围大于非隔离DC/DC变换器,因此广泛应用于电网的中小功率离线式变换器当中。隔离半桥电路是一个典型的高阶、非线性、离散系统,其电路动态解析方法复杂。为解决工程应用中变换器的设计问题,建模分析是必不可少的环节。变换器的建模方法一般可分为两大类:数字仿真法和解析建模法[1-3]。解析法大多数是在理想状态下的建模,不利于提高建模精度。而能量守恒平均法考虑了变换器寄生参数的影响,因此建模精度进一步提高。

本文利用能量守恒原理将变换器寄生参数进行理想化转换,在得到隔离半桥电路平均模型的基础上,导出交流小信号模型。进一步分析,得到整个系统的开环传递函数及合适的补偿参数,在仿真与实验平台上对隔离半桥电路进行补偿参数调整和输出预测,结果验证理论分析的正确性。

1 隔离半桥电路建模

1.1 能量守恒平均模型

隔离半桥电路原理如图1所示;隔离半桥寄生元件等效电路如图2所示。图中,功率开关VT1等效为理想开关S1与其导通电阻rDS的串联,二极管VD1等效为理想开关SD1、电压源UF和二极管导通电阻rD的串联。rT1为变压器一次侧绕组电阻,rT2为变压器二次侧绕组电阻,rL为电感寄生电阻,C为滤波电容,R为负载电阻。

图1 隔离半桥电路原理

图2 隔离半桥寄生元件等效电路

在建模过程中,假设:电压源的输出电阻为零;所有无源元件是线性不变器件;功率开关的输出电容可以忽略不计[4-8]。

能量守恒平均原理是以器件损耗不变为原则,将多个元件寄生参数产生的损耗等效为一个寄生参数产生的损耗,将一个开关周期内各个时间产生的损耗平均到整个开关周期。运用替代定理将功率开关等效为电流源,二极管等效为电压源,隔离半桥电路的大信号平均模型如图3所示。图3中,iL为流过电感L的瞬时电流,那么TS为一个开关周期内流过电感L的平均电流;iS为流过功率开关的瞬时电流,TS为一个开关周期内流过功率开关的平均电流。UD为二极管耐压值,D为驱动脉冲占空比,n=n1∶n2为变压器变比。二极管等效电压源为二极管一个周期内承受耐压值UD=UID/2n,功率开关等效电流源为一个周期内功率开关流过的平均电流TS=D/nTS。

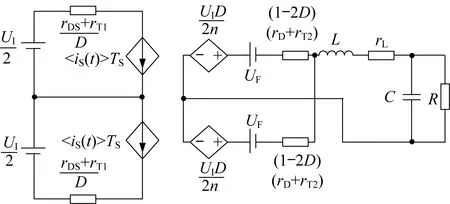
图3 隔离半桥电路大信号平均模型

在隔离半桥电路中,功率开关导通时间与驱动脉冲占空比相同,且导通后流过功率开关瞬时电流iS=iL/n,则一个开关周期内流过功率开关的电流有效值IS为

(1)

功率开关导通电阻rDS及变压器一次侧绕组电阻rT1的功率损耗为

(2)

由式(2)可得隔离半桥电路原边电阻的等效平均值Req1=(rDS+rT1)/D。

以二极管VD1为例,当上管导通下管关断时,流过二极管瞬时电流iD=iL;当下管导通上管关断时,流过二极管瞬时电流iD=0;当上管与下管同时关断电感L续流时,流过二极管瞬时电流iD=iL/2。一个周期内二极管电流有效值ID为

(3)

二极管导通电阻rD及变压器二次侧绕组电阻rT2的功率损耗为

(4)

由式(4)可得二极管导通电阻及变压器二次侧绕组电阻的等效平均值为Req2=(1-2D)(rD+rT2)。

图3经戴维南等效,并将一次侧电阻等效到二次侧后,隔离半桥电路简化大信号平均模型如图4所示。

图4 隔离半桥电路简化大信号平均模型

(5)

1.2 小信号线性模型

将隔离半桥大信号等效电路中的平均量分离扰动,分解为相应的交流分量和交流小信号分量[9-11]。

忽略其中的高阶微小量,得到小信号模型。隔离半桥电路交流小信号模型如图5所示。

图5 隔离半桥电路交流小信号模型

由图5可得,输出电压与占空比的关系,此时令UI=0,得到电感电流为

(9)

则隔离半桥电路传递函数为

(10)

2 闭环系统开环传递函数及补偿参数设计

2.1 闭环系统结构

隔离半桥电路闭环系统结构如图6所示。由驱动电路、PWM调制器、补偿网络、隔离半桥功率电路以及采样电路构成。系统选用SG3525作为控制芯片,调制方式为PWM调制。其工作原理是:误差放大器将输出电压采样信号Uf与基准电压信号Uref的差值进行补偿放大,放大的误差信号Ue与固定斜率的谐波信号Ur进行比较,产生所需的PWM信号。

图6 隔离半桥电路闭环系统结构

2.2 PWM调制器

脉宽调制器实际上是一个电压比较器。PWM调制电路如图7所示,比较器同相输入端Uc为补偿网络的输出电压,反向输入端是幅值为Um,周期为T的锯齿波Ue。通过开环实验,测得SG3525的锯齿波峰峰值为2.4 V,比较器的输出是一个占空比为d的脉冲,PWM调制器的传递函数Fm(s)为

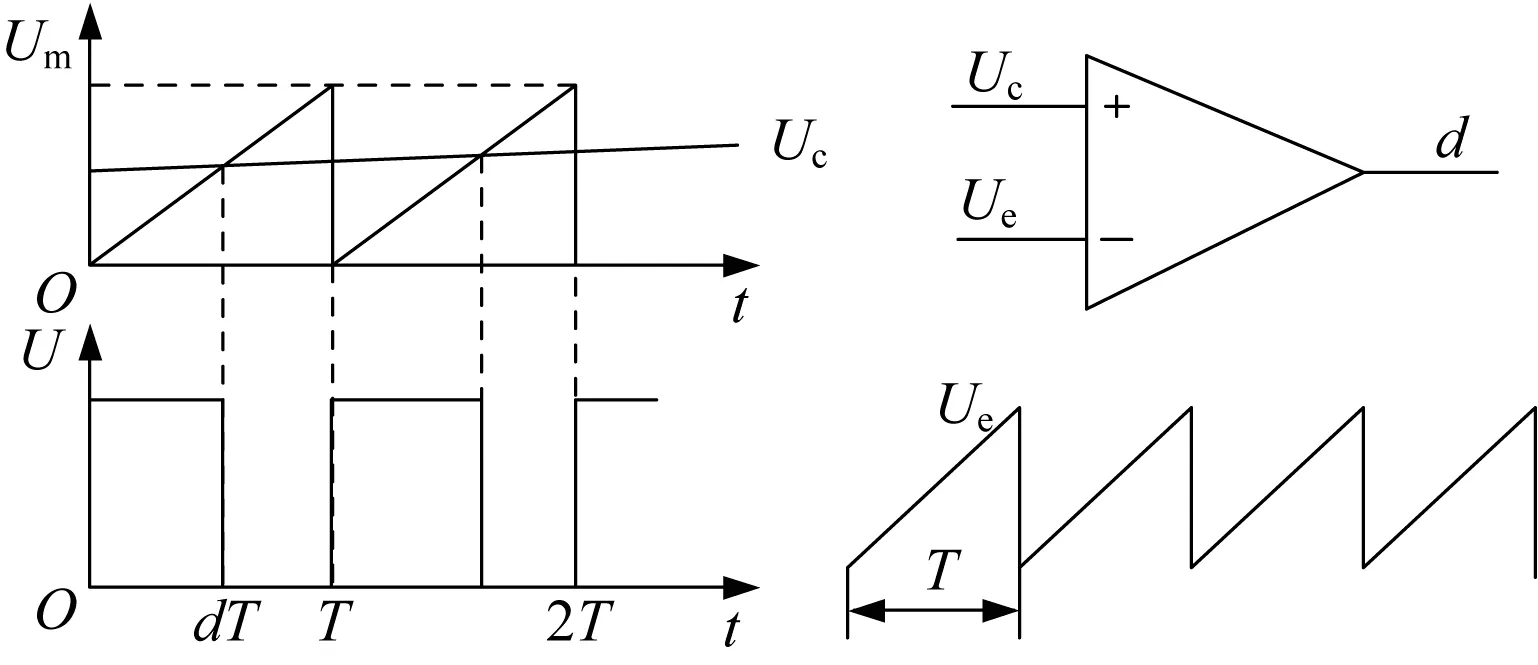
图7 PWM调制电路

(11)

2.3 采样电路

采样电路如图8所示。电压传感器的转换率p为2 500∶1 000,且一次侧内电阻Rin为250 Ω,采样回路的传递函数为

图8 采样电路

(12)

2.4 补偿网络及其参数计算

开关电源设计中,变换器补偿网络的良好设计可以显著提高电源的性能。在SG3525的内部设有误差放大器,在误差放大器的补偿端加上补偿网络可实现不同方式的补偿,本文采用常见的PI补偿方式。PI补偿网络如图9所示。

图9 PI补偿网络

由图9可导出PI补偿网络的传递函数Gc(s)为

(13)

其中,

(14)

隔离半桥电路输入电压UI=24 V,负载电阻R=100 Ω,负载滤波电容C=1 200 μF,电感L=0.2 mH,驱动脉冲占空比D=0.45,变压器变比n为0.16,功率开关导通电阻rDS=0.03 Ω,变压器一次侧绕组电阻rT1=0.2 Ω,二极管导通电阻rD=0.44 Ω,变压器二次侧绕组电阻rT2=1.7 Ω,电感寄生电阻rL=0.3 Ω。根据图6以及上述各部分电路传递函数推导,在无补偿情况下系统的开环传递函数为

G(s)=H(s)Fm(s)Gvd(s)=

(15)

在一定频率范围内穿越频率越大,则环路增益越大,从而系统具有更好的输出阻抗和噪声抑制能力。但在实际设计中不能无限增大穿越频率,根据采样定理,开关电源的带宽应小于开关频率的1/2,为提高稳定性和减少开关噪声的影响,开关电源的带宽通常介于开关频率的1/5～1/10。已知半桥电路开关频率约在30 kHz,则穿越频率在3～6 kHz较为合适。

将系统开环传递函数代入Sisotool工具箱并设置穿越频率为3.3 kHz,相位裕度为60°。补偿前后Bode图如图10所示。

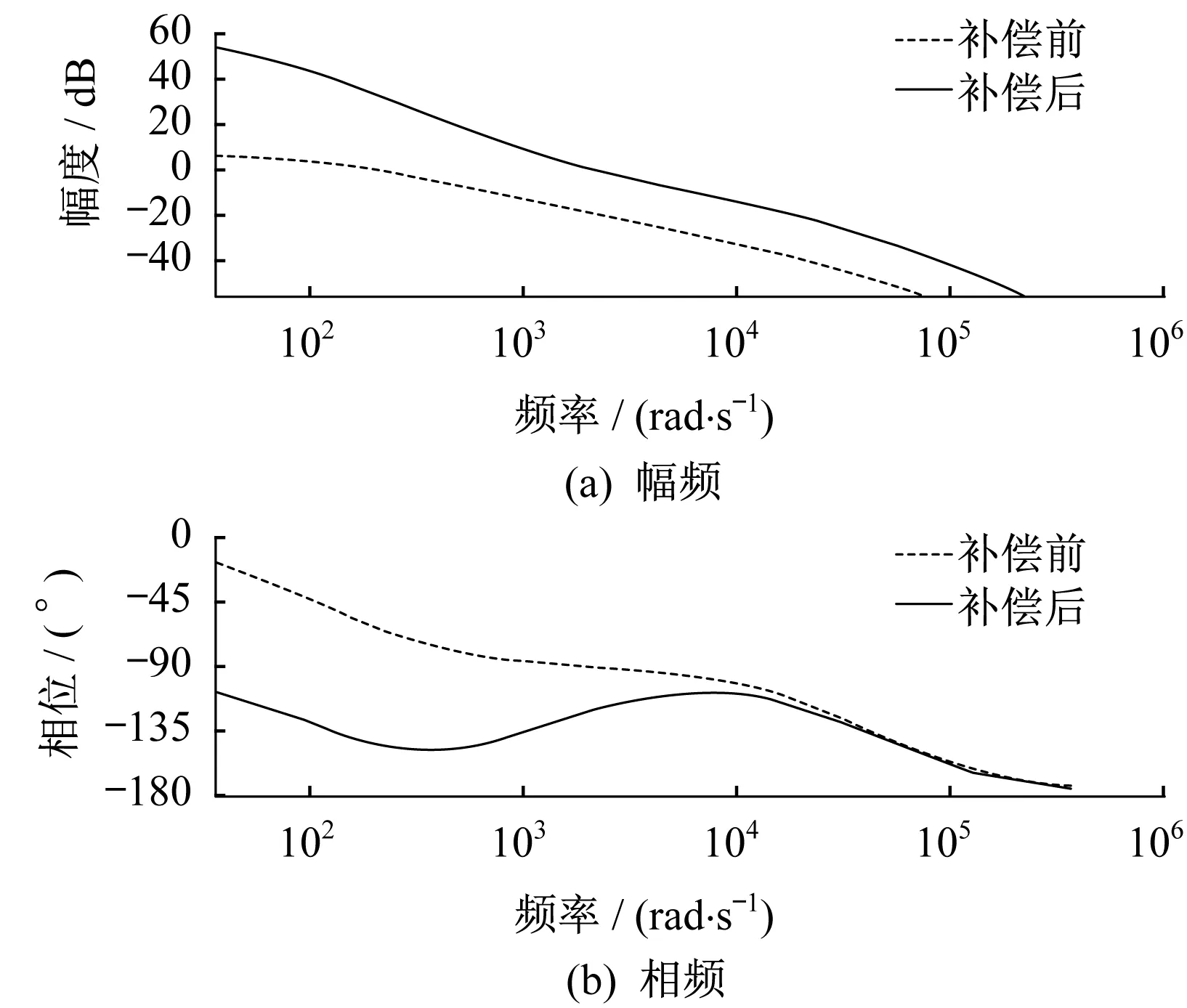
图10 补偿前后系统Bode图

由图10可知,补偿前系统低频增益太低,系统稳态性能较差,中频段穿越频率较低,无法保证足够的动态响应能力,因此需要提高系统的低频增益以及穿越频率。经过补偿后幅值裕度为正,相位裕度为60°,满足系统稳定性要求。且低频增益在40 dB以上,满足系统零稳态误差的要求,中频段系统的穿越频率约在3.3 kHz,且以接近-20 dB/(°)的斜率穿过0 dB线,满足系统动态响应要求,高频段幅频曲线以接近-40 dB/(°)的斜率快速衰减,对高频噪声起抑制作用[12]。

在设计中已知R1=2.4 kΩ,根据式(14)可求得C1=42 nF,R2=20 kΩ,即该补偿参数能保证整个系统具有较好的动态性能及稳定性,称该补偿参数为理想补偿参数,该补偿网络为理想补偿网络。

3 仿真与实验

根据理论分析并搭建仿真与实验平台,运行时隔离半桥电路输入电压Uin=24 V,额定输出电压Uo=48 V,开关频率fs=30 kHz,变压器变比n=8∶50∶50,负载电阻R=100 Ω,电感L=0.2 mH。

3.1 仿真验证

为验证建模的可靠性以及补偿网络的适用性,利用Saber仿真软件搭建隔离半桥电路。通过仿真电路修改补偿参数及负载大小,得到一系列仿真波形。不同补偿参数下仿真输出电压波形如图11所示。

图11 不同补偿参数下仿真输出电压波形

图11(a)为额定负载情况下无补偿网络与理想补偿网络时输出电压波形,显然在理想补偿网络时输出电压稳定较快且稳定后纹波较小。

图11(b)为在额定负载情况下,补偿网络中电阻R2分别为2 kΩ、20 kΩ以及55 kΩ时输出电压波形。电阻R2=2 kΩ时,输出电压稳定较慢且纹波较大,电阻R2=20 kΩ时,输出电压稳定较快且稳定后纹波较小,虽然电阻R2=55 kΩ时输出电压稳定最快,但稳定时间较R2=20 kΩ并没有较大提升,且R2阻值大小与比例系数p成正相关,p值太大可能会出现发散振荡。

图11(c)为在额定负载情况下,补偿网络中电容C1分别为4.2 nF、42 nF以及200 nF时输出电压波形,电容C1=4.2 nF时,输出电压虽超调量较小但输出电压稳定较慢,电容C1=200 nF时,输出电压虽能快速稳定但超调量过大。

图11(d)为理想补偿参数情况下负载突变时输出电压波形,0～0.25 s时给电路加100 Ω负载,在0.25 s时给电路加200 Ω负载,0.5 s时给电路加500 Ω负载,在不同负载情况下电路输出电压都能快速稳定。通过上述4组仿真结果,验证了该补偿参数的合理性。

3.2 实验验证

不同补偿参数下实际输出电压波形如图12所示。图12(a)与12(b)分别为无补偿网络与理想补偿网络情况下的输出电压波形。图12(c)与12(d)对应补偿网络中不同电阻值R2的输出电压波形。图12(e)与12(f)对应补偿网络中不同电容值C1的输出电压波形。对比各输出电压波形,在无补偿网络时虽然电压过冲小,但输出电压不稳定,纹波较大。电阻值R2过小时,输出电压稳定较慢,电阻值R2过大时,输出电压稳定速度与理想补偿网络并没有较大提升,同时较大的p值可能会引起发散振荡。电容值C1过小时,虽输出电压过冲值较小但稳定较慢,电容值C1过大时,虽输出电压能快速稳定但过冲值较大。在理想补偿网络情况下,输出电压能快速稳定且纹波较小,在电压上升过程中过冲值较小。图12(g)是在理想补偿网络情况下负载电阻突变时输出电压波形,可知系统较为稳定且输出电压能快速稳定。

图12 不同补偿参数下实际输出电压波形

综上所述,在仿真与实验条件保持一致的情况下,实验结果也基本一致。通过修改电阻及电容参数的对比实验,充分验证了该补偿参数的合理性。

4 结 语

本文运用能量守恒原理建立了隔离半桥电路的交流小信号模型,经过对隔离半桥电路开环传递函数的理论研究得到适合隔离半桥电路闭环系统的补偿参数,并在仿真与实验中通过多组数据对比验证了补偿参数设计的合理性。整个系统的抗干扰能力和动态性能得到改善,说明了基于能量守恒原理建立的隔离半桥电路交流小信号模型对电路控制环路设计具有指导及实用借鉴意义。