从2021、2020两年高考试题看不等式选讲解题方略

游少华

摘 要：本文通过对近几年高考绝对值不等式选作题分析，总结重视函数图象来认识不等关系，并从函数图象来分析解证不等式及求不等式中的变量范围.

关键词：全国高考;绝对值不等式求解;函数图象

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）10-0047-03

课标卷中的两道选作题，学生如何选择，如何解答非常重要，甚至决定学生考试的成败.这两道题都体现数学的核心素养——数形结合的思想.但对不等式而言，无论是有变量问题还是定量不等式问题，学生都习惯分类讨论求解.分类讨论除分类不清外，还存在求交集错误問题，不等关系其本质上是函数图象的上下关系.如果能作图象解不等式，不但直观展现大小关系，更能方便看出不等关系的变量范围.

2021年与2020年两年的考题都体现这一解题思想.

题1 （2021年全国文理甲卷）

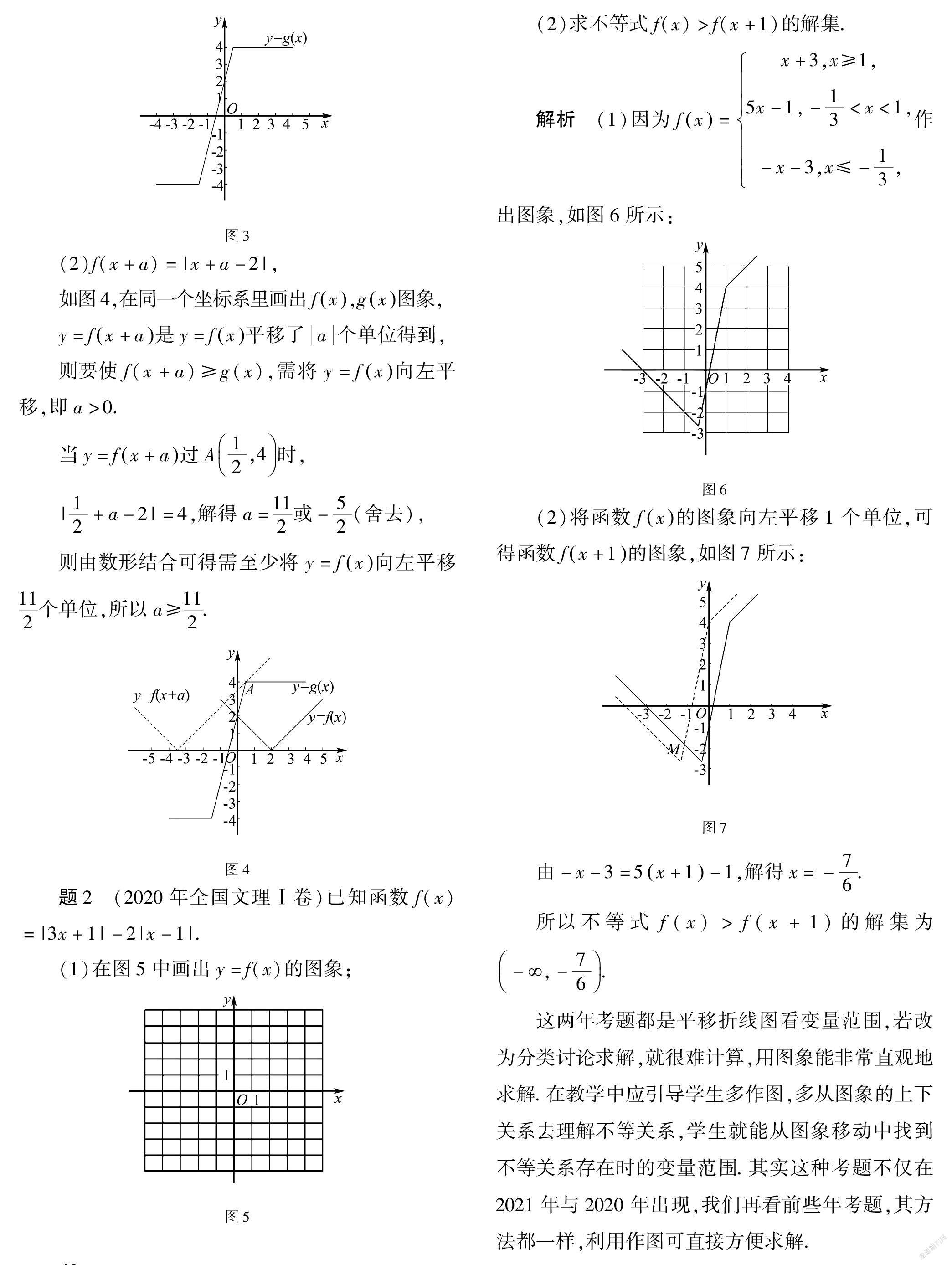
已知函数f（x）=x-2，g（x）=2x+3-2x-1.

（1）在图1中画出y=fx和y=gx的图象;

（2）若fx+a≥gx，求a的取值范围.

解析 （1）可得f（x）=x-2=2-x，x<2，x-2，x≥2，画出图象如图2：

g（x）=2x+3-2x-1

=-4，x<-32，4x+2，-32≤x<124，x≥12，画出函数图象如图3：

（2）f（x+a）=|x+a-2|，

如图4，在同一个坐标系里画出fx，gx图象，

y=fx+a是y=fx平移了a个单位得到，

则要使f（x+a）≥g（x），需将y=fx向左平移，即a>0.

当y=fx+a过A12，4时，

|12+a-2|=4，解得a=112或-52（舍去），

则由数形结合可得需至少将y=fx向左平移112个单位，所以a≥112.

题2 （2020年全国文理Ⅰ卷）已知函数f（x）=|3x+1|-2|x-1|.

（1）在图5中画出y=f（x）的图象;

（2）求不等式f（x）>f（x+1）的解集.

解析 （1）因为fx=x+3，x≥1，5x-1，-13

（2）将函数fx的图象向左平移1个单位，可得函数fx+1的图象，如图7所示：

由-x-3=5x+1-1，解得x=-76.

所以不等式f（x）>f（x+1）的解集为-SymboleB@，-76.

这两年考题都是平移折线图看变量范围，若改为分类讨论求解，就很难计算，用图象能非常直观地求解.在教学中应引导学生多作图，多从图象的上下关系去理解不等关系，学生就能从图象移动中找到不等关系存在时的变量范围.其实这种考题不仅在2021年与2020年出现，我们再看前些年考题，其方法都一样，利用作图可直接方便求解.

题3 （2018年全国Ⅲ卷文理）设函数f（x）=|2x+1|+|x-1|.

（1）在图8中画出y=f（x）的图象;

（2）当x∈[0，+SymboleB@）时，f（x）≤ax+b，求a+b的最小值.图8

解析 （1）f（x）=-3x，x<-12，x+2，-12≤x<1，3x，x≥1.

y=f（x）的图象如图9所示.

（2）由（1）知，y=f（x）的图象与y轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3.

故当且仅当a≥3且b≥2时，

f（x）≤ax+b在[0，+SymboleB@）成立，

因此a+b的最小值为5.

题4 （2013年全国Ⅰ卷文理）已知函数f（x）=|2x-1|+|2x+a|，g（x）=x+3.

（1）当a=-2时，求不等式f（x）

（2）设a>-1，且当x∈[-a2，12）时，f（x）≤g（x），求a的取值范围.

解析 （1）当a=-2时，不等式f（x）

设函数y=|2x-1|+|2x-2|-x-3，

y=

-5x，x<12-x-2，12≤x≤1，3x-6，x>1

其图象如图10所示，从图象可知，当且仅当x∈（0，2）时，y<0.

所以原不等式解集是{x|0

（2）当∈[-a2，12）时，f（x）=1+a，不等式f（x）≤g（x）化为1+a≤x+3.

所以x≥a-2对

x∈[-a2，12）都成立.

故-a2

≥a-2.

即a≤43.

所以a的取值范围为（-1，43].

参考文献：

[1]

杜志建.十年高考真题汇编[M].乌鲁木齐：新疆青少年出版社，2019.

[2] 中华人民共和国教育部考试中心.中国高考评价体系说明[M].北京：人民教育出版社，2019.

[责任编辑：李 璟]